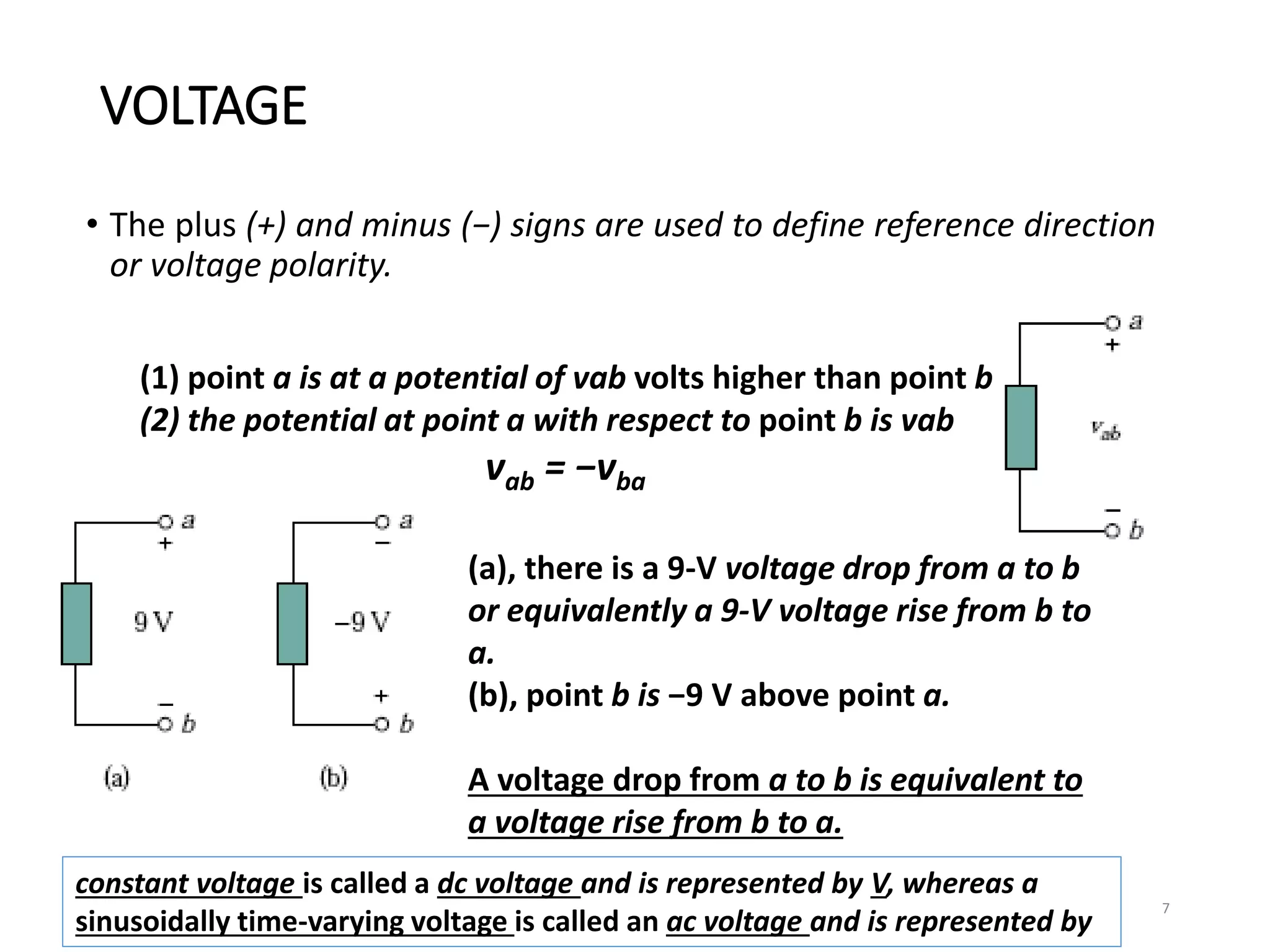
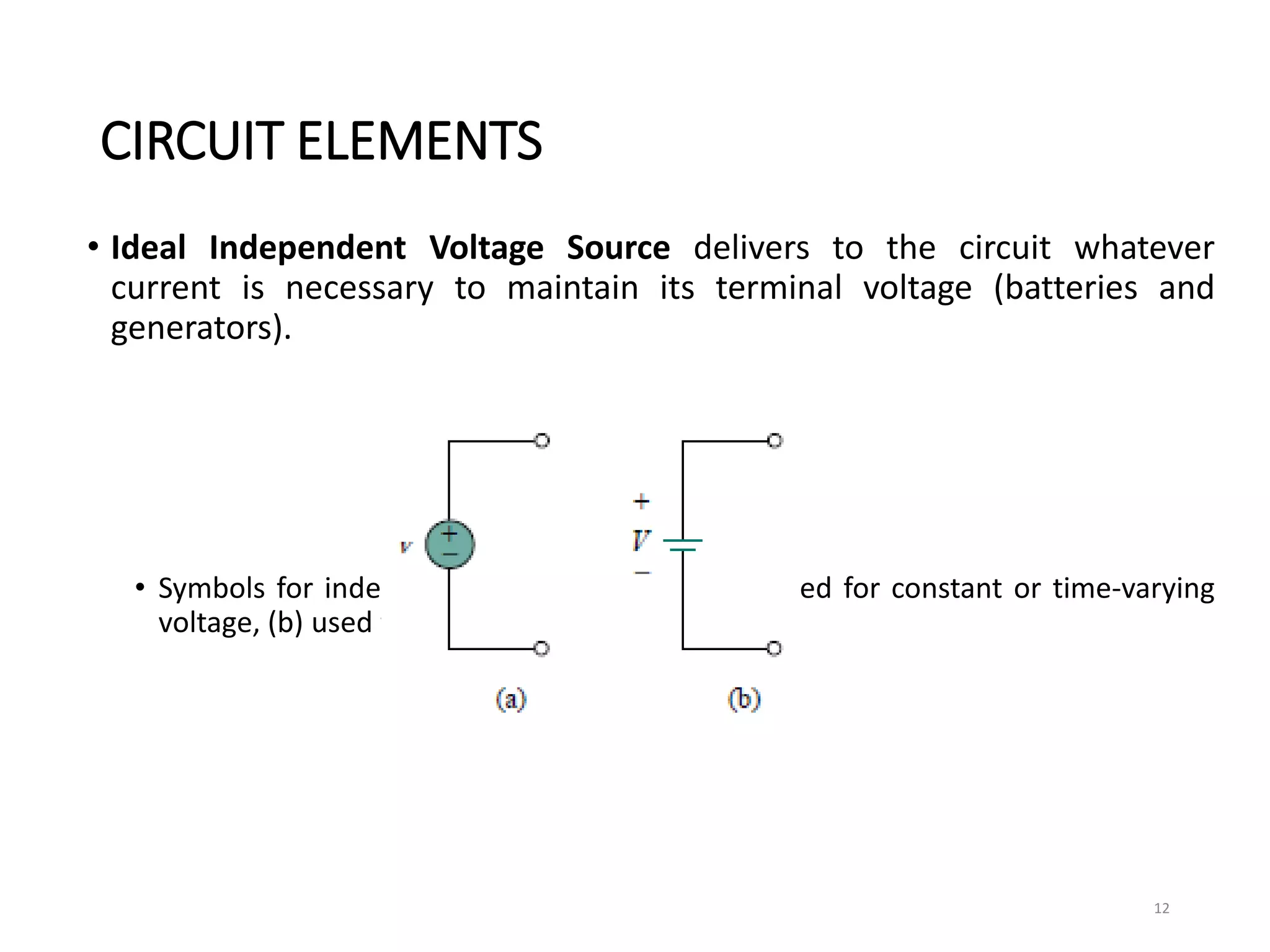
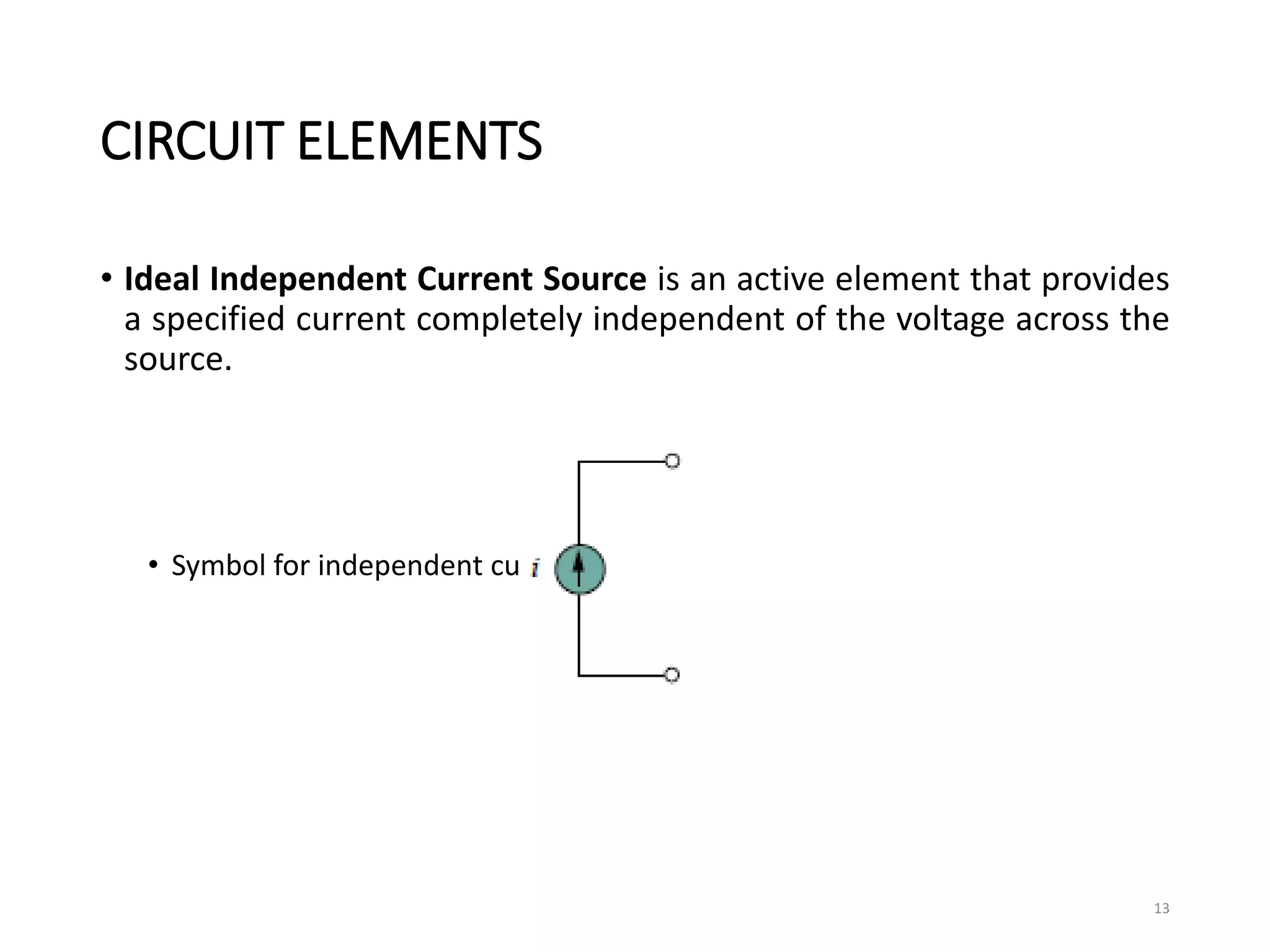
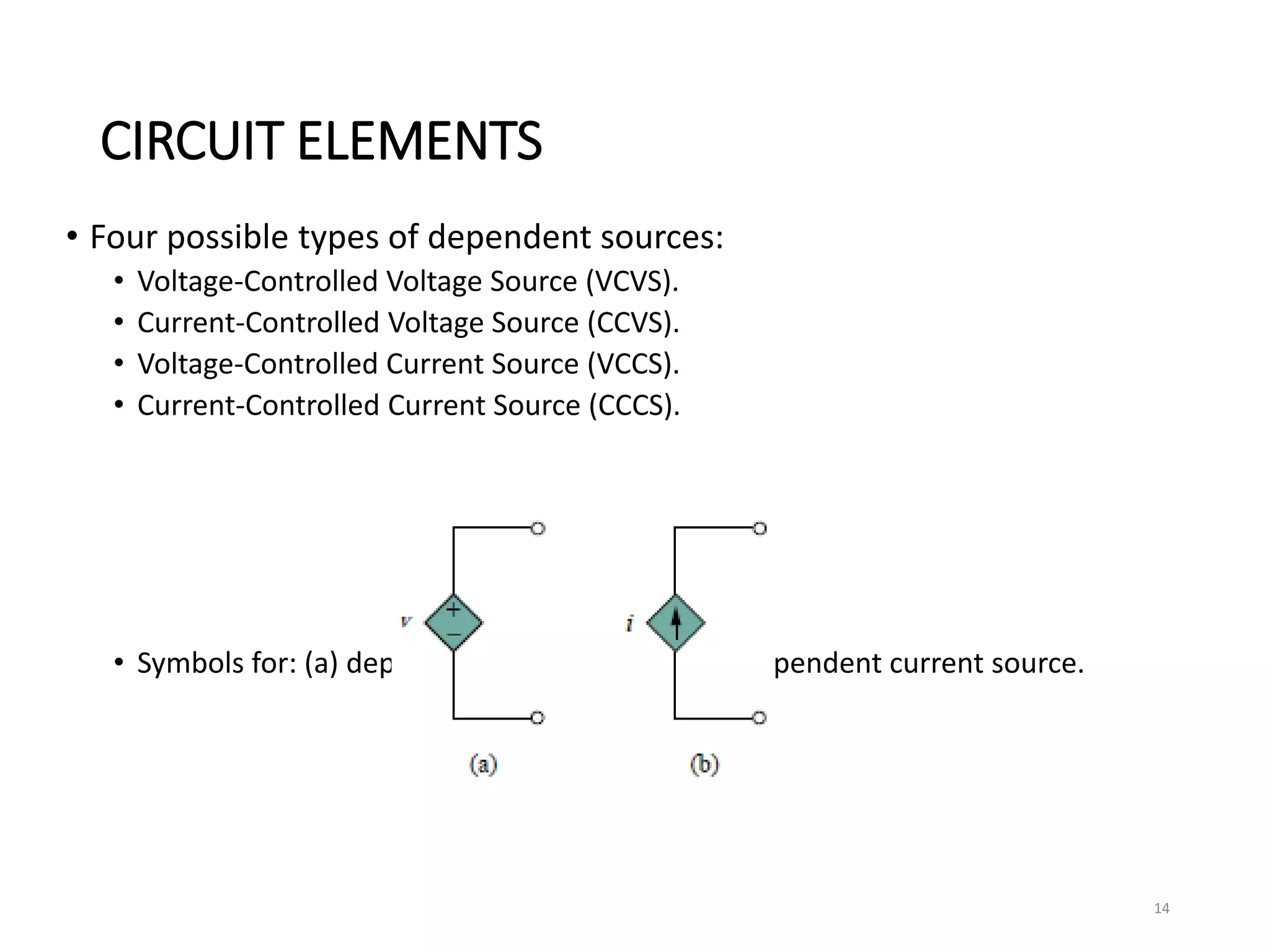
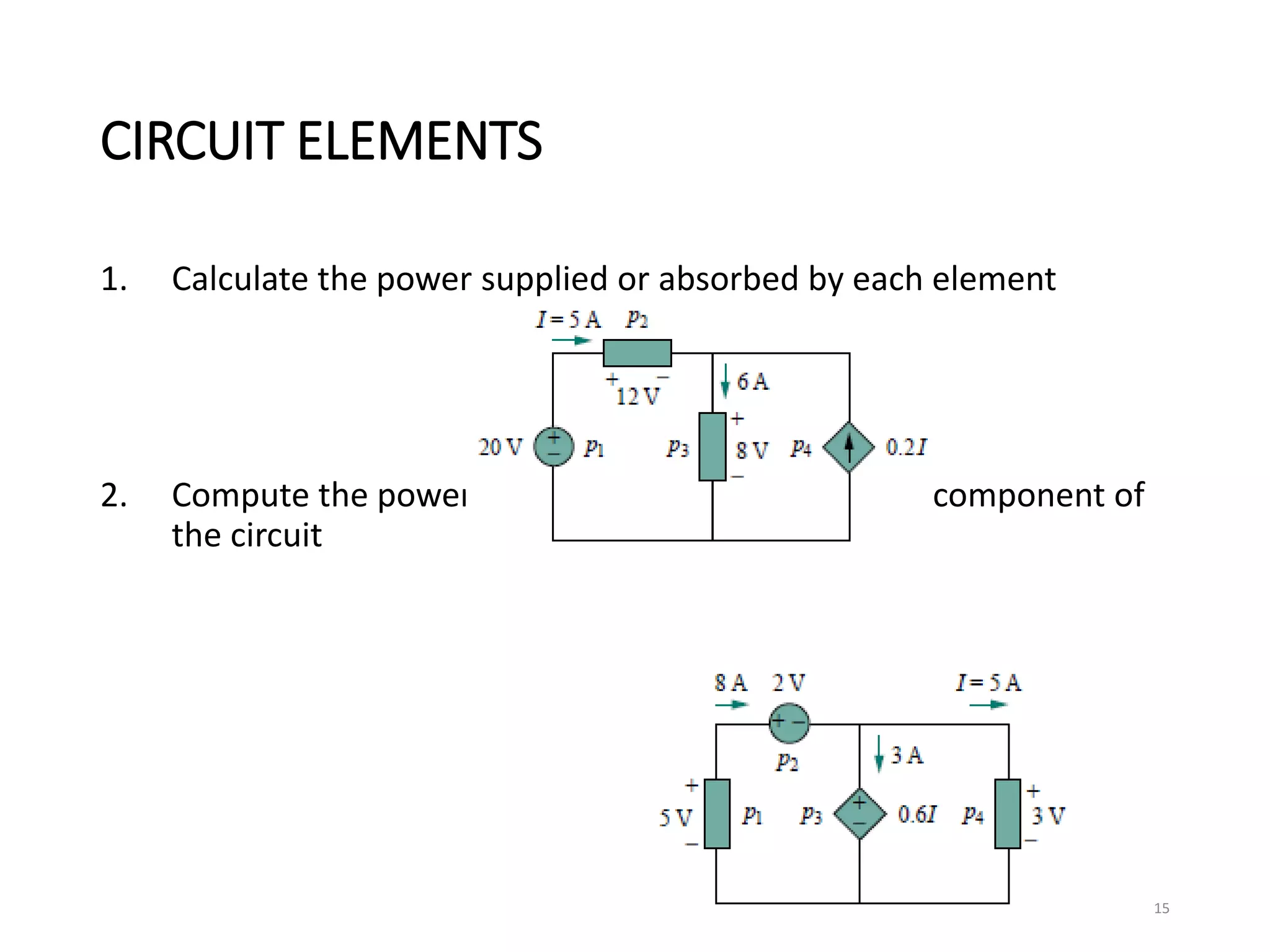
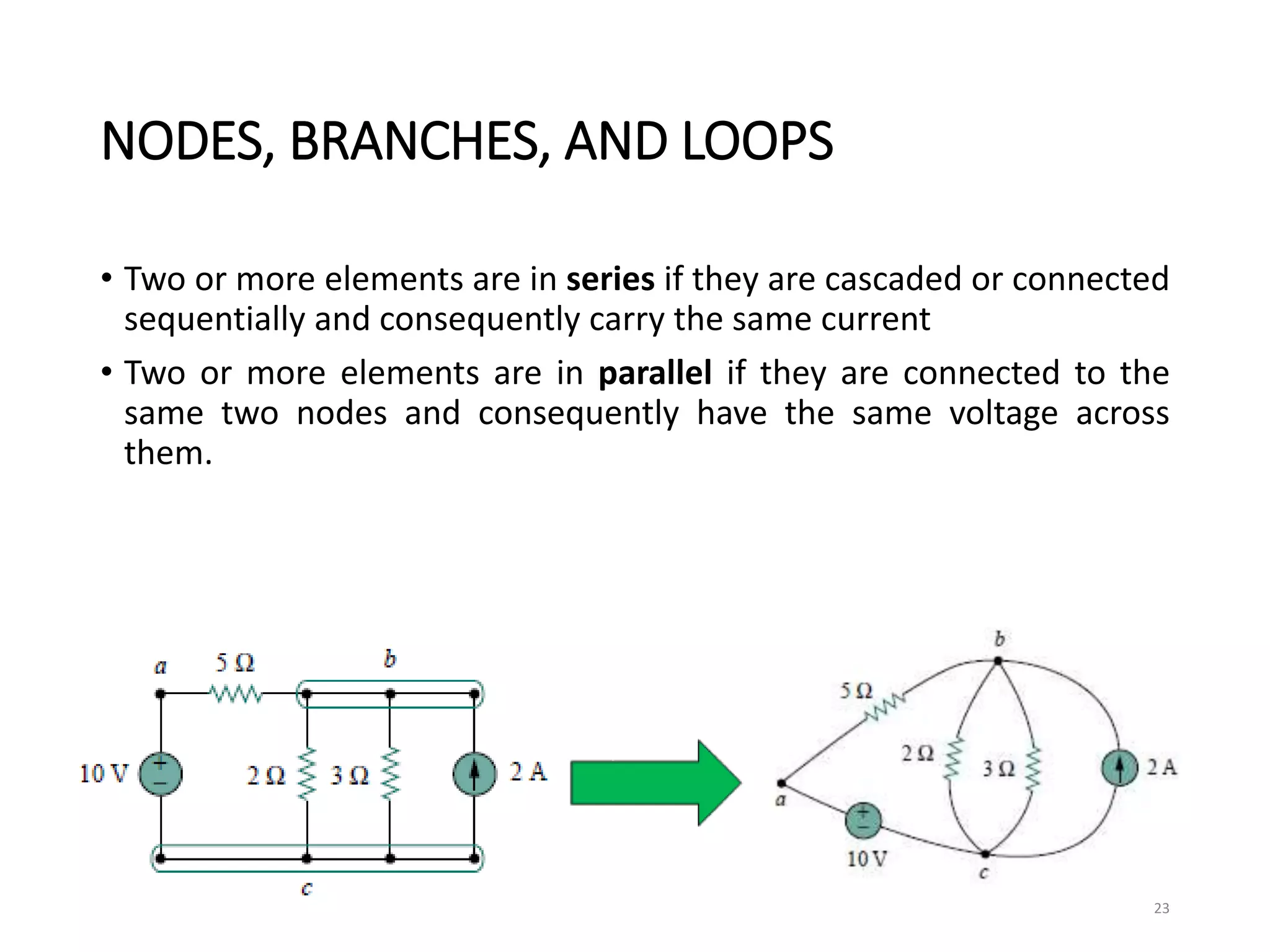
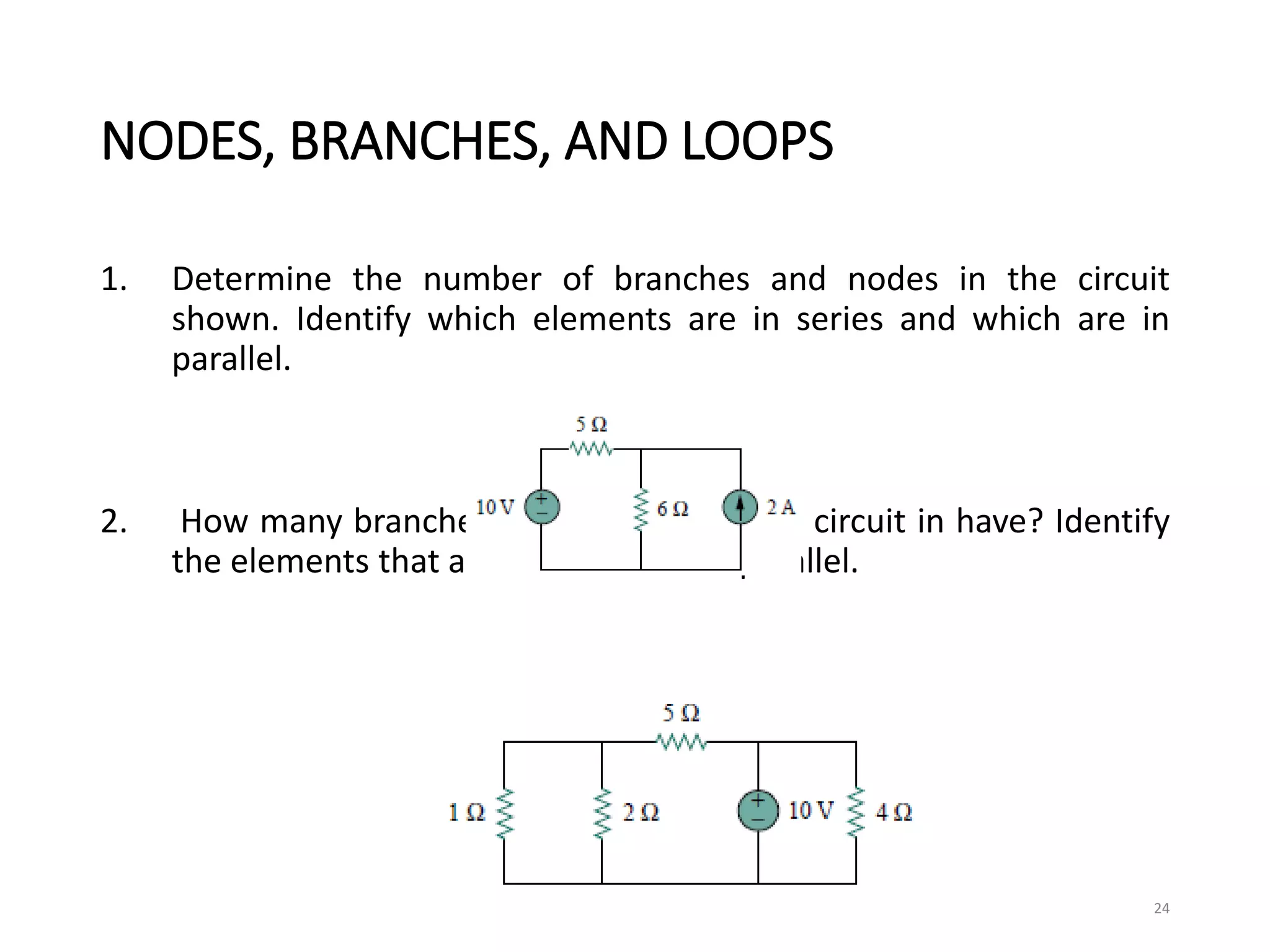
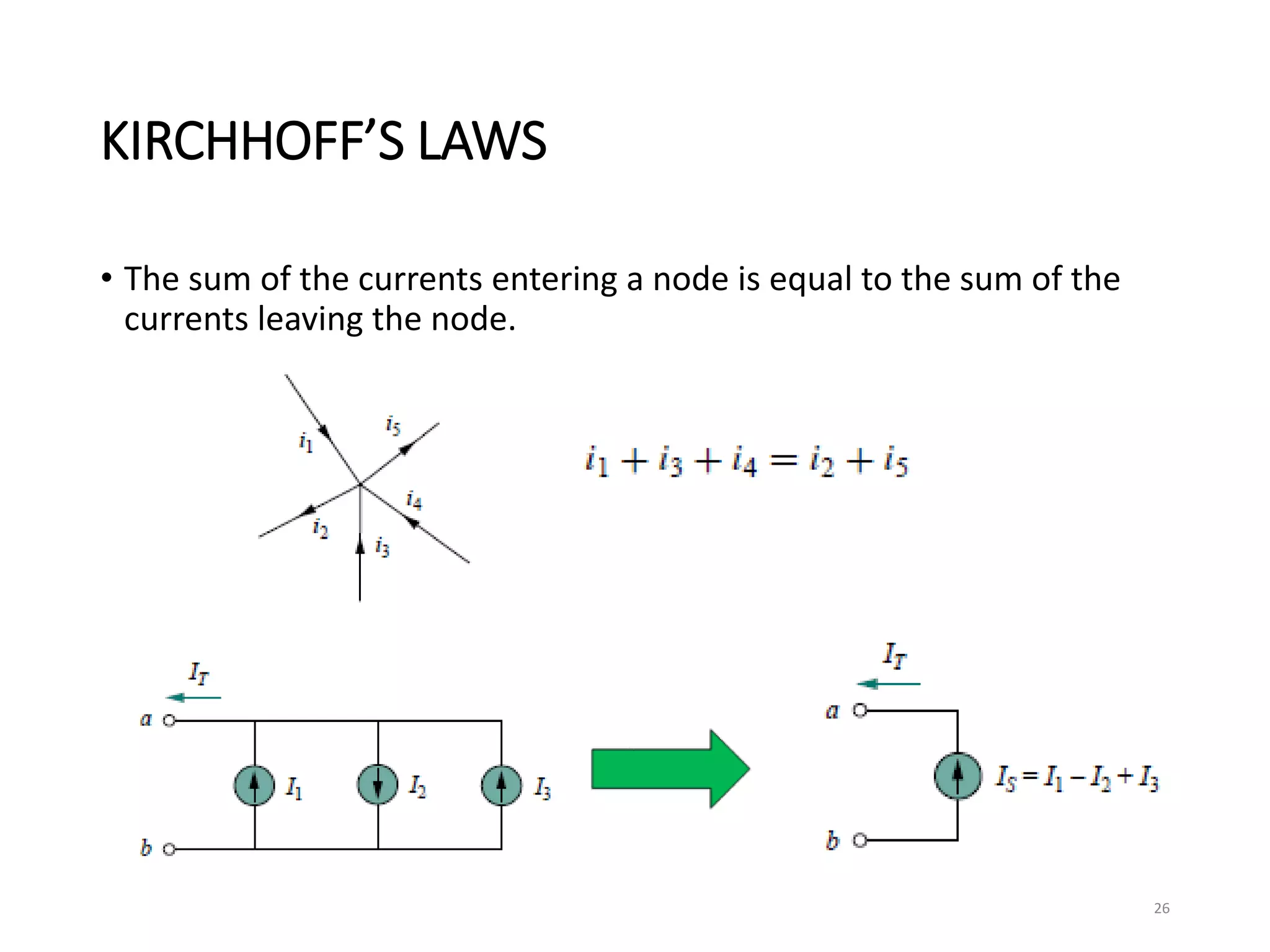
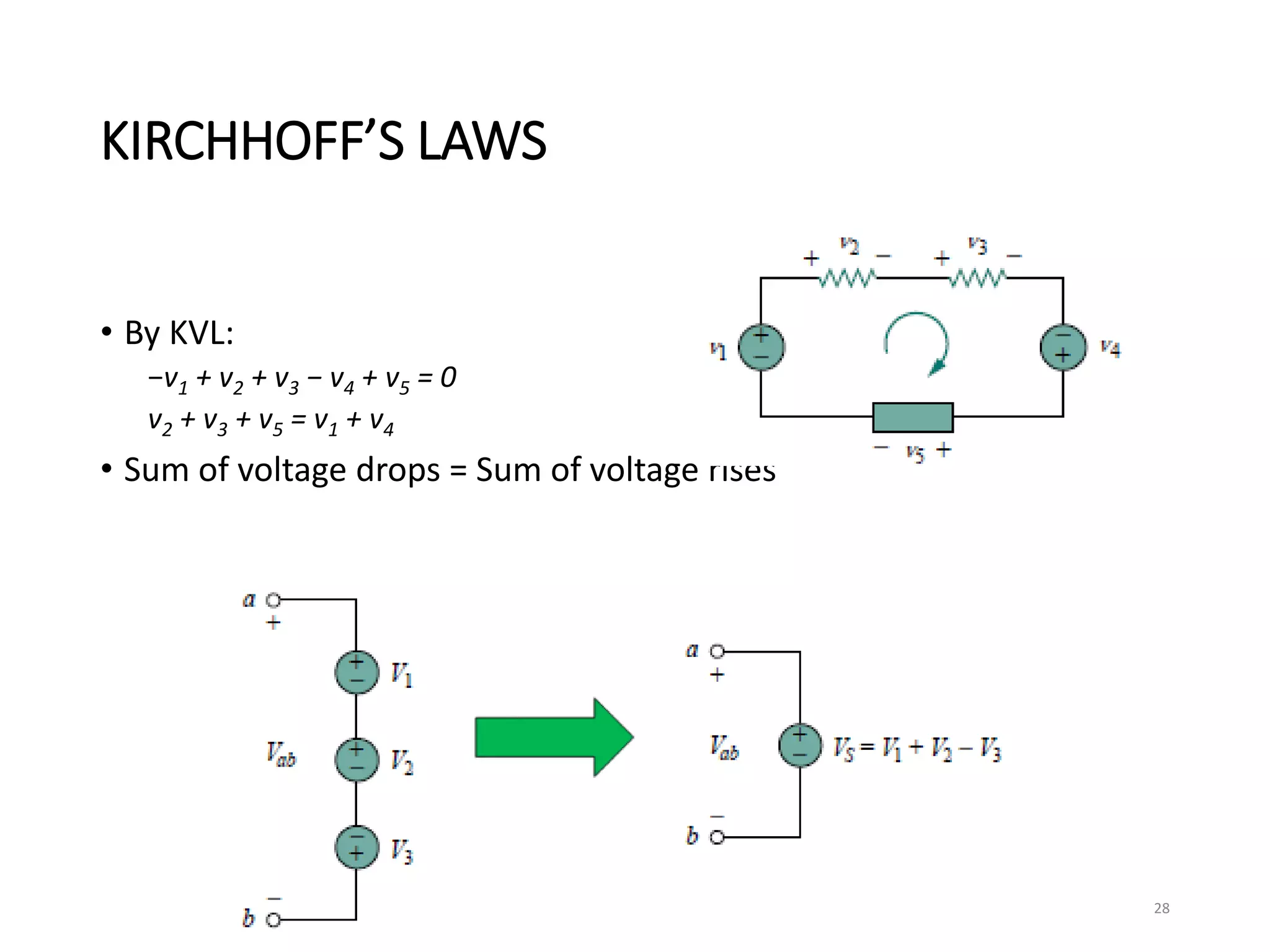
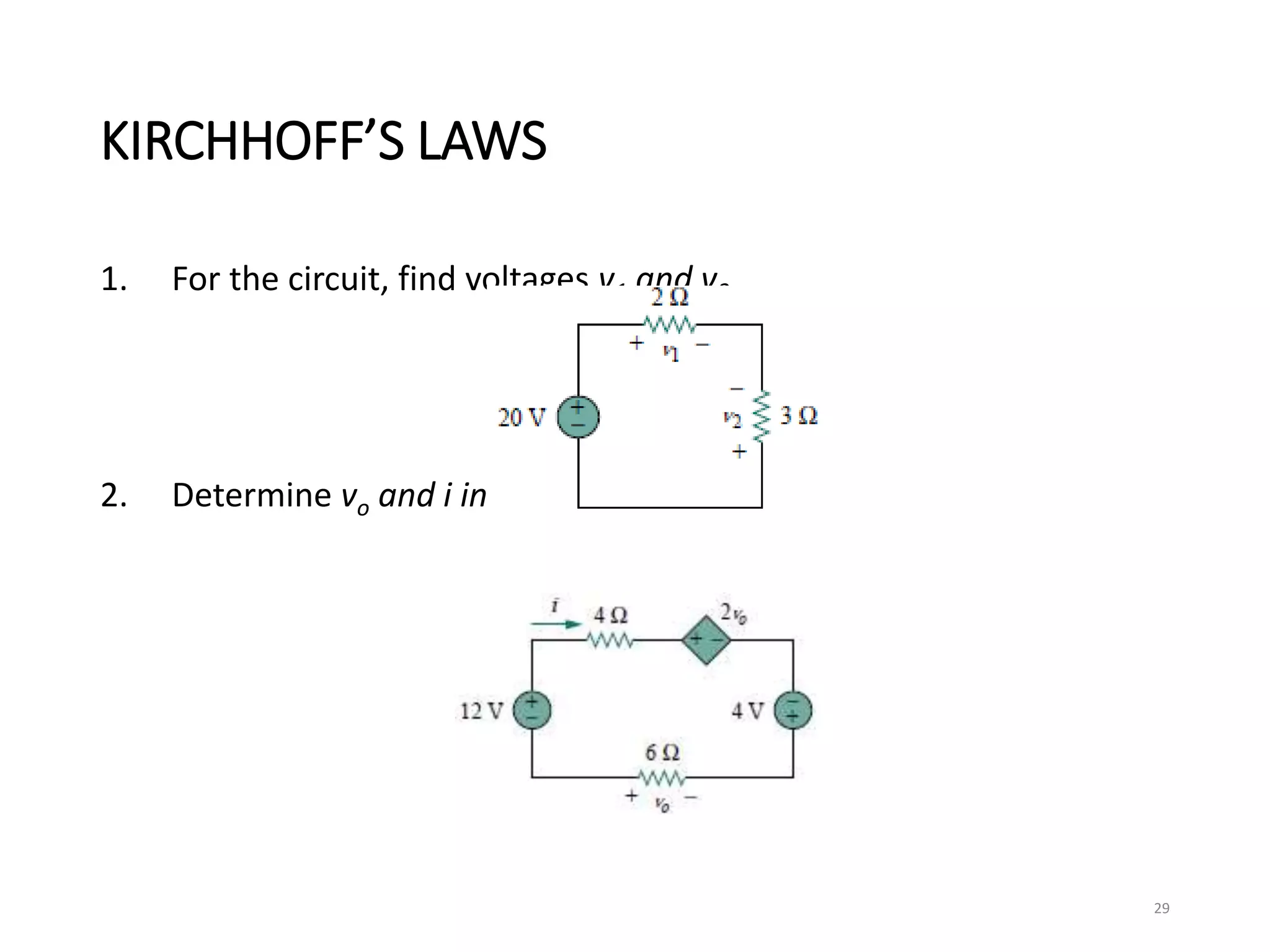
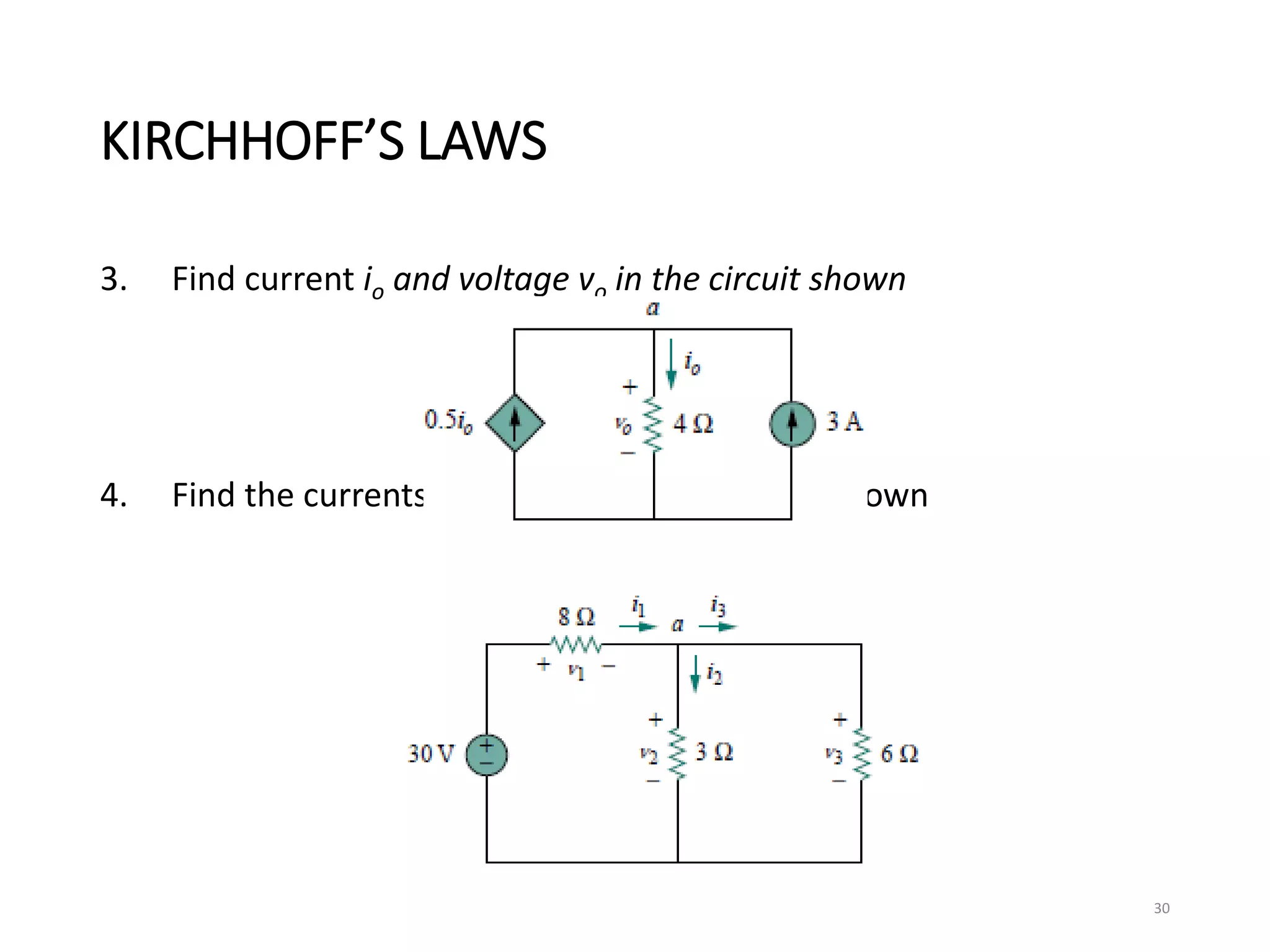
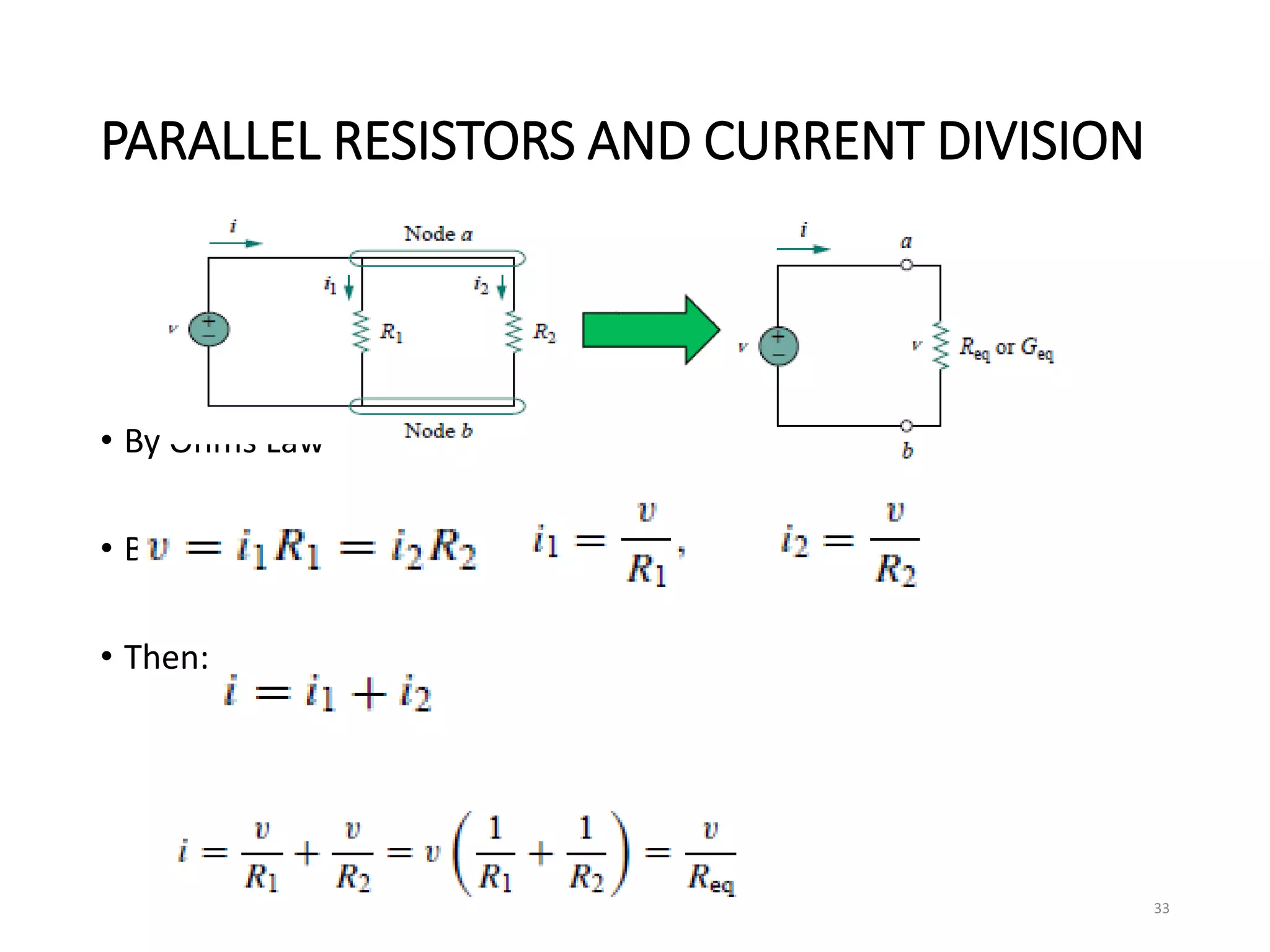
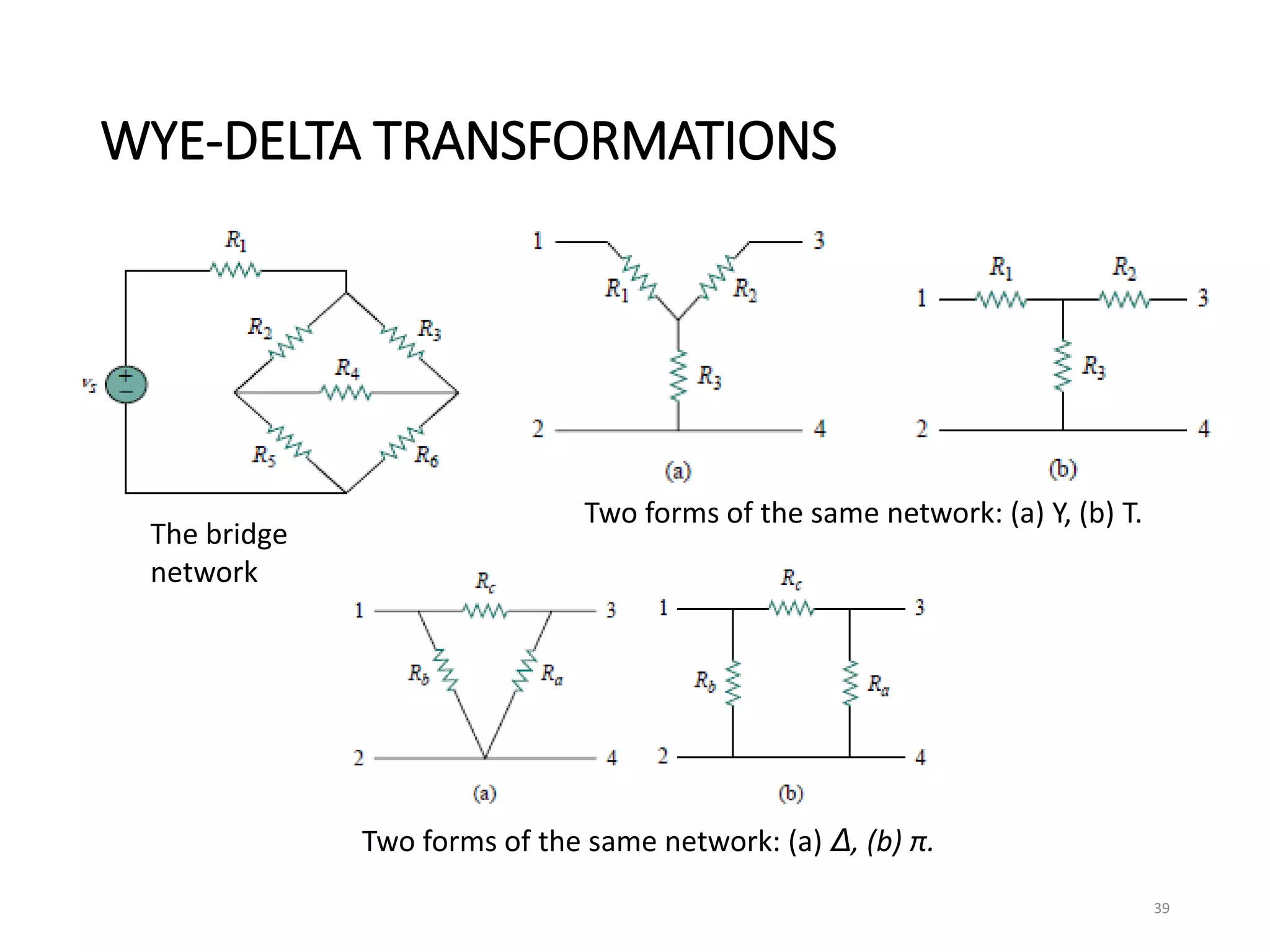
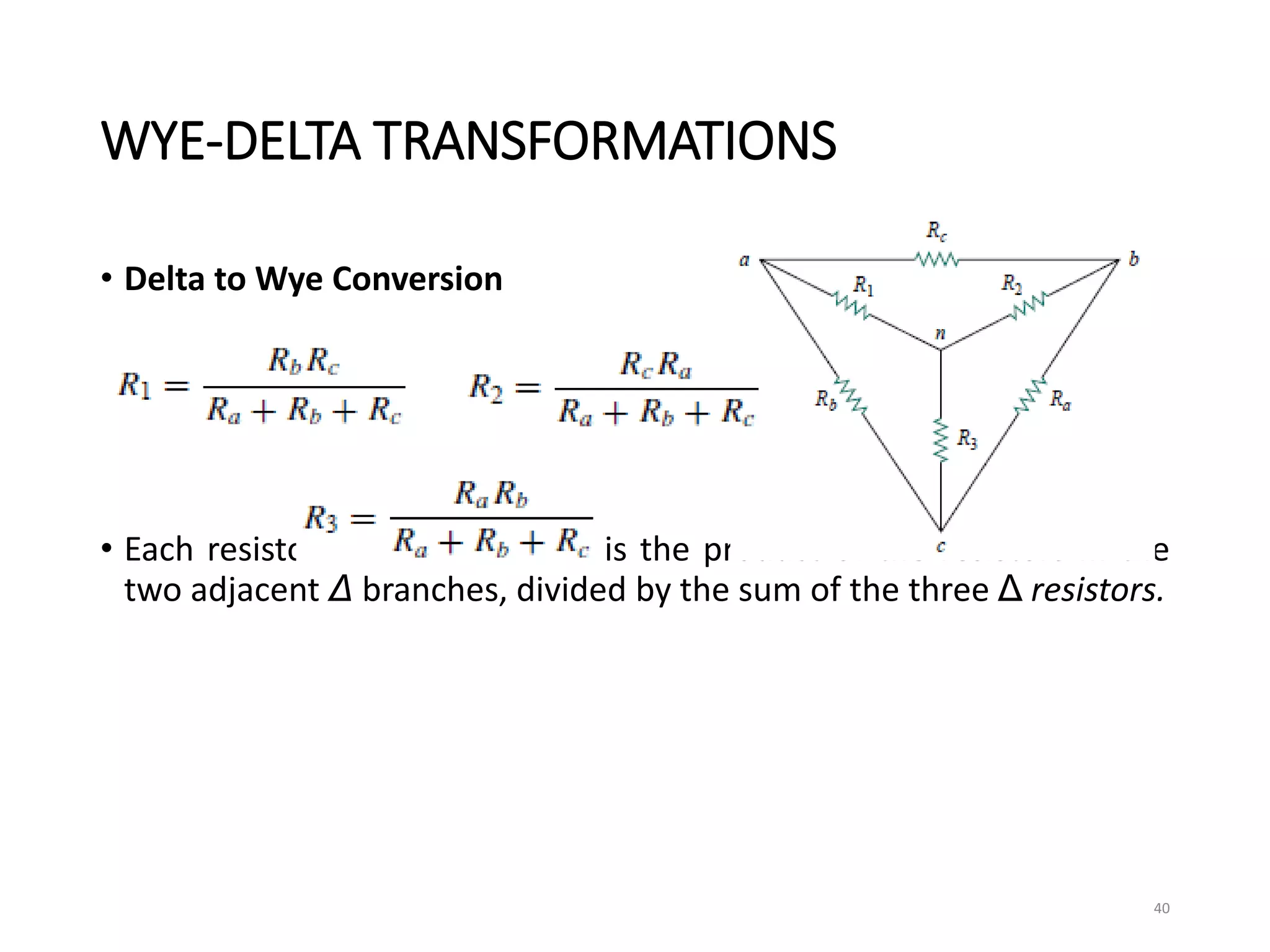
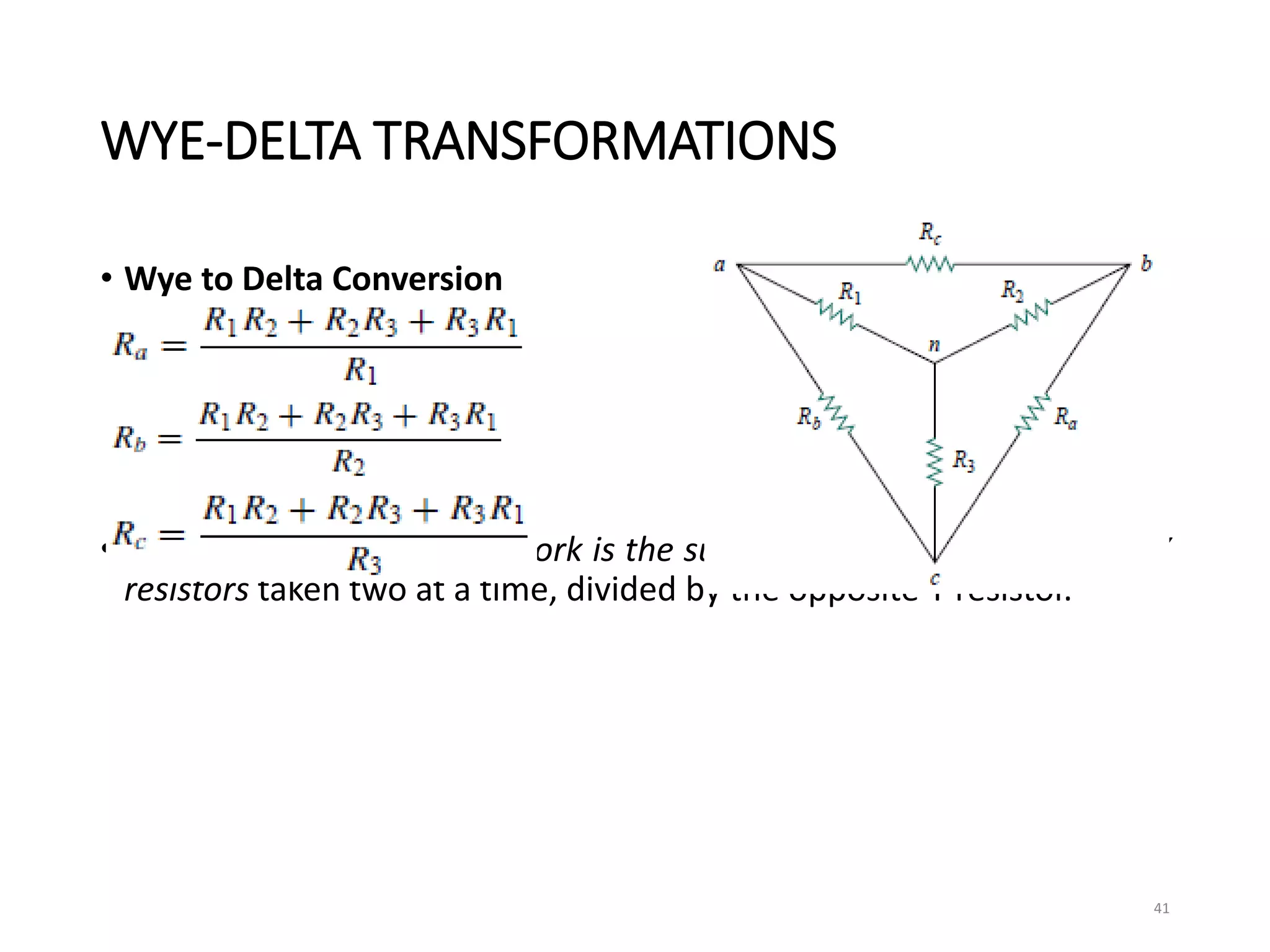
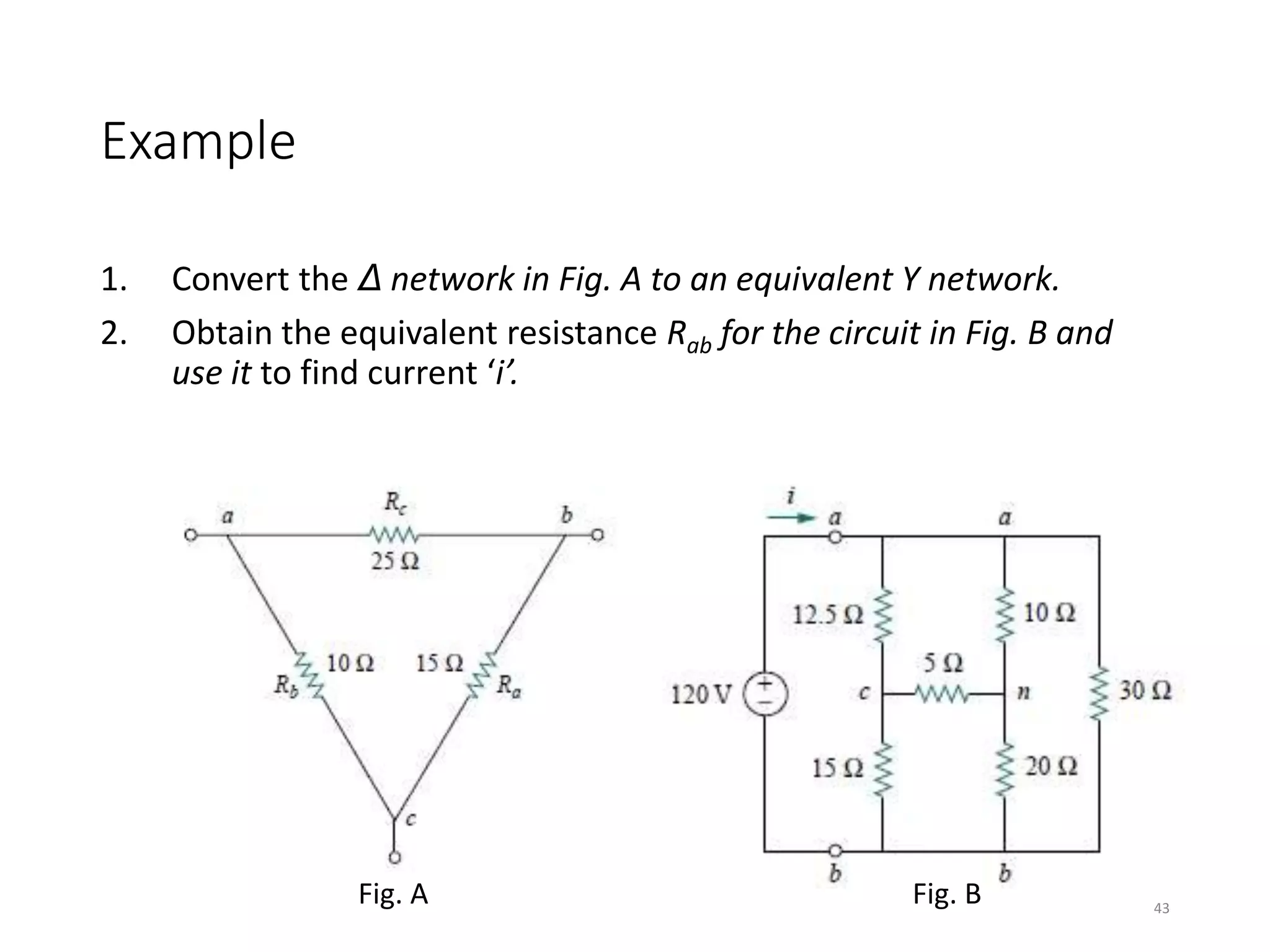
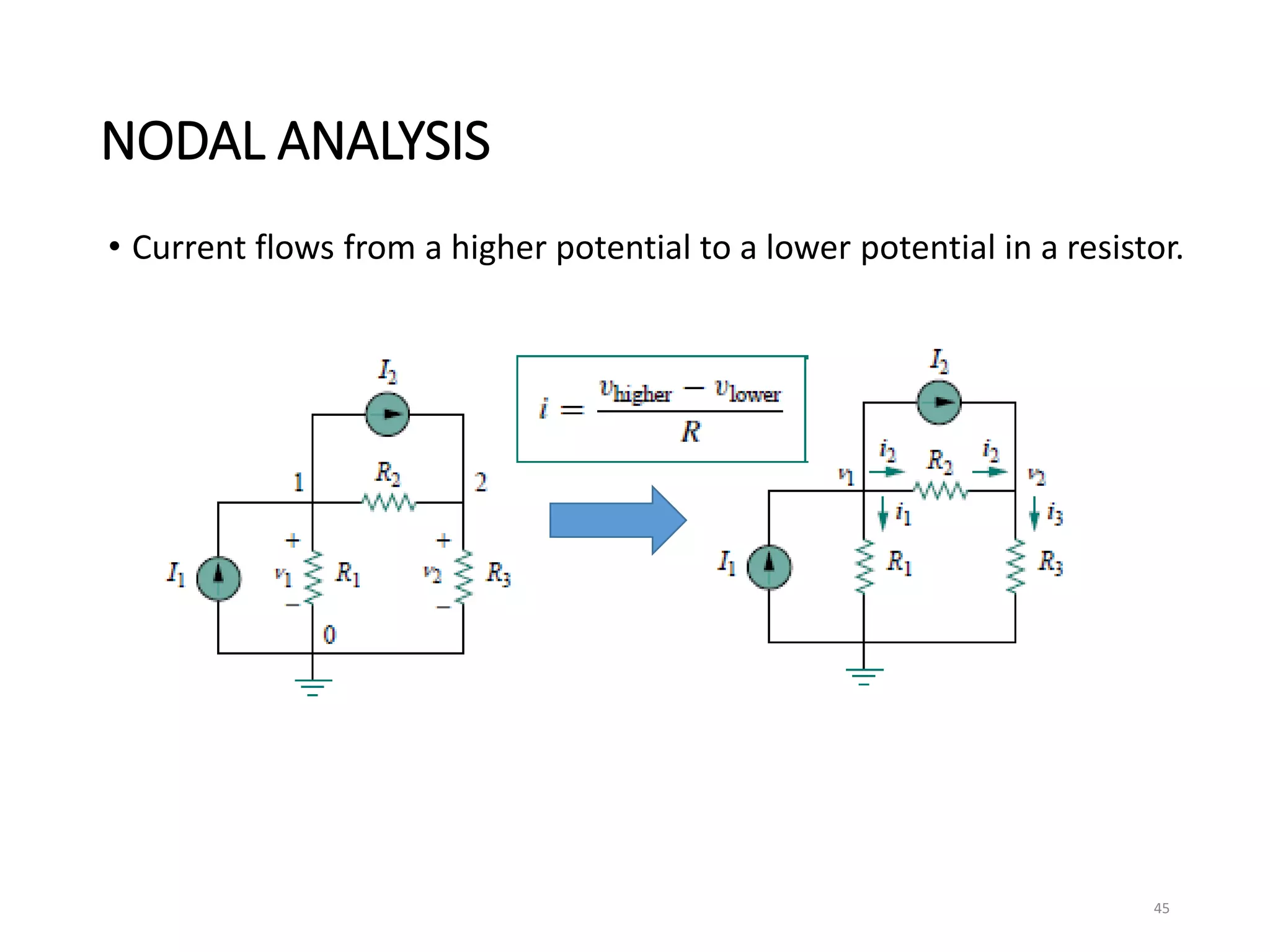
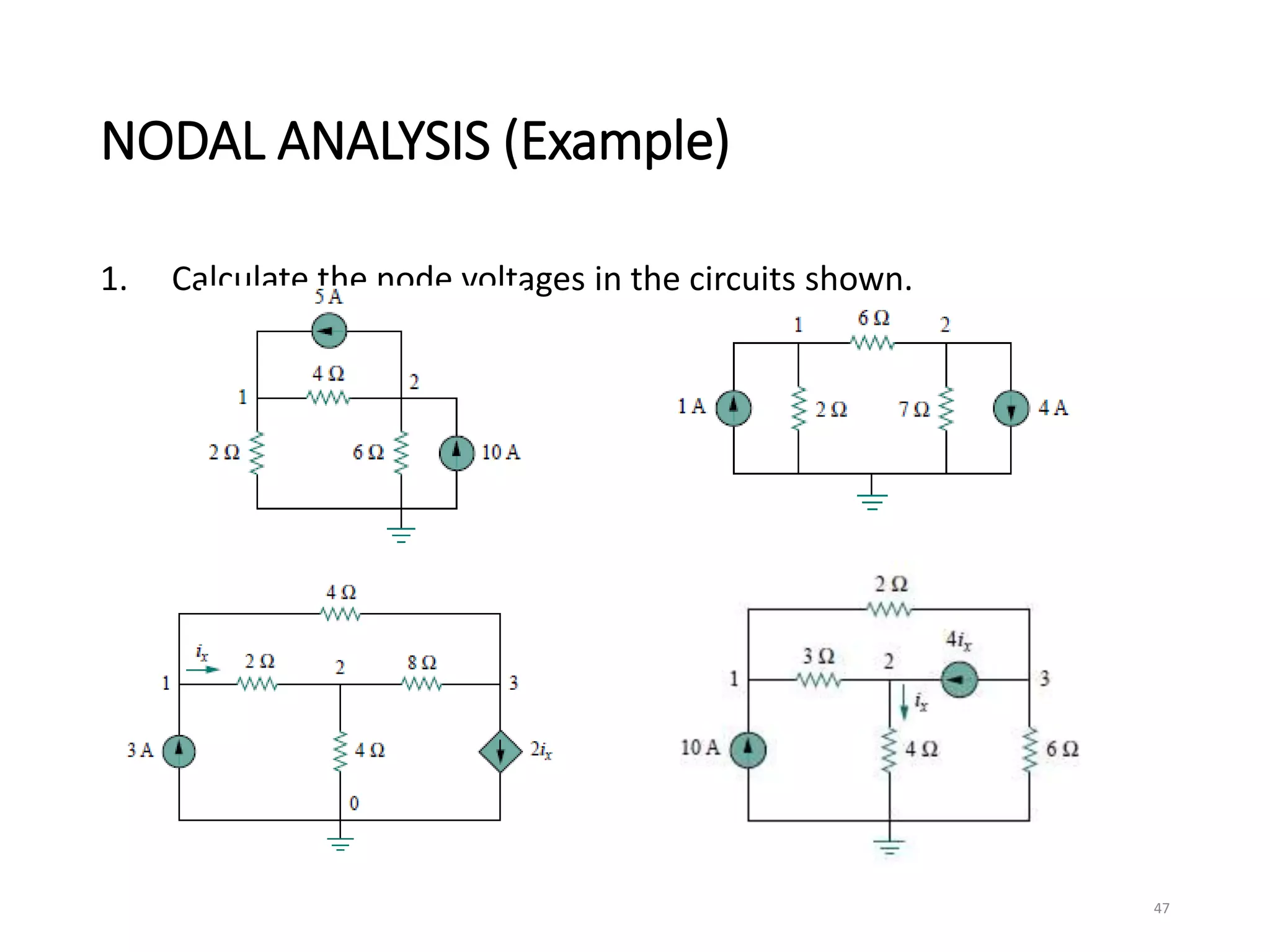
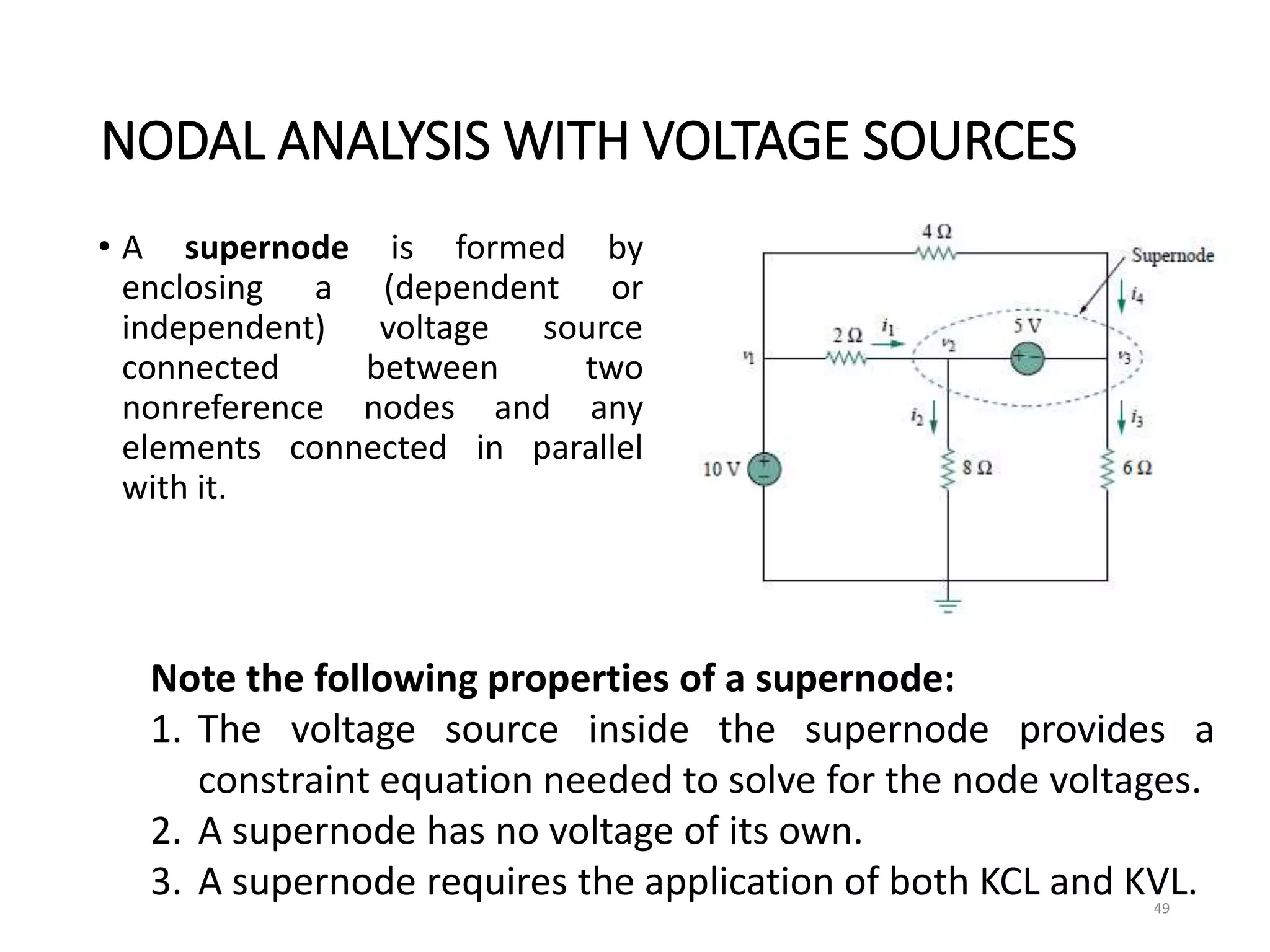
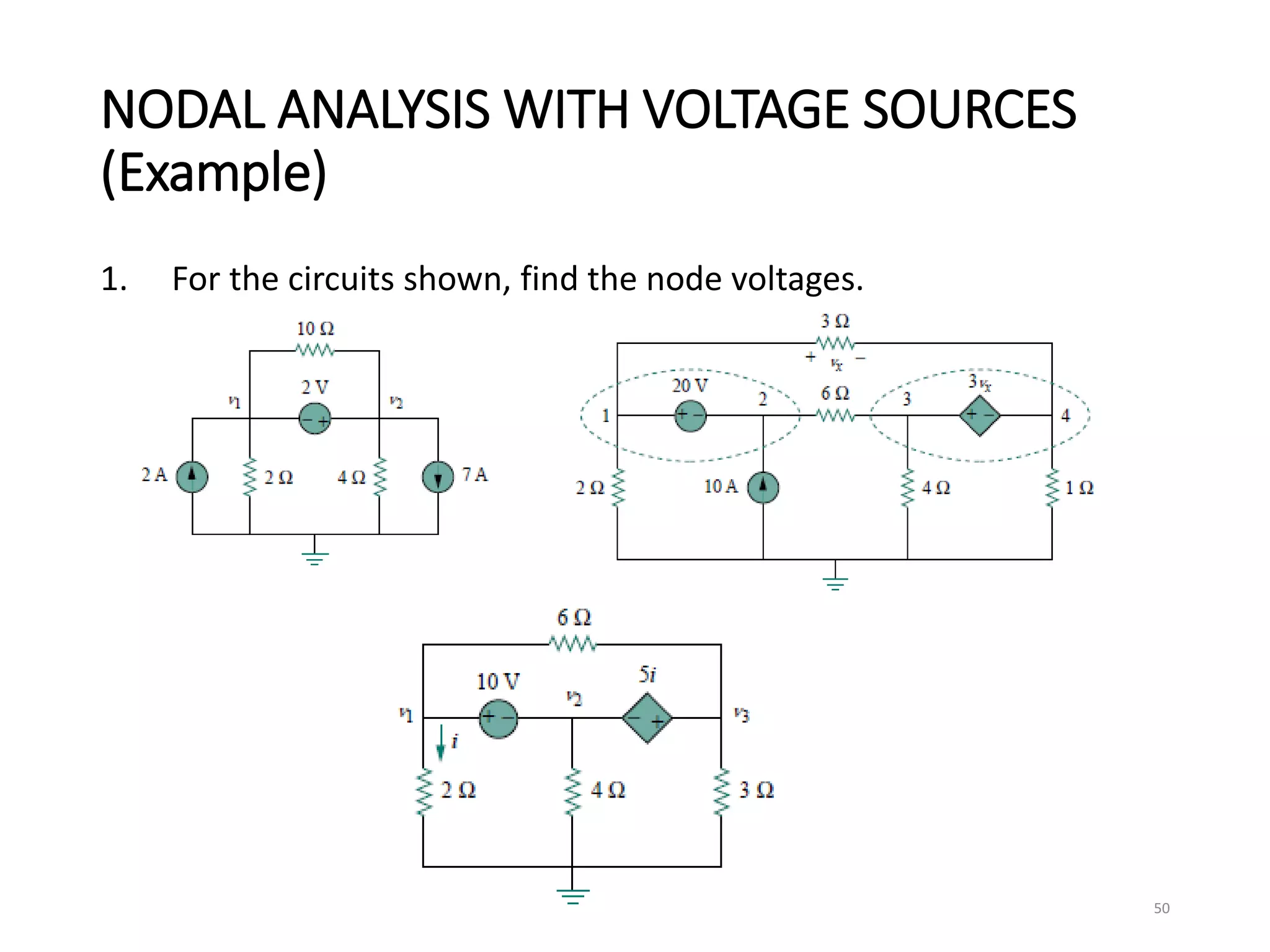
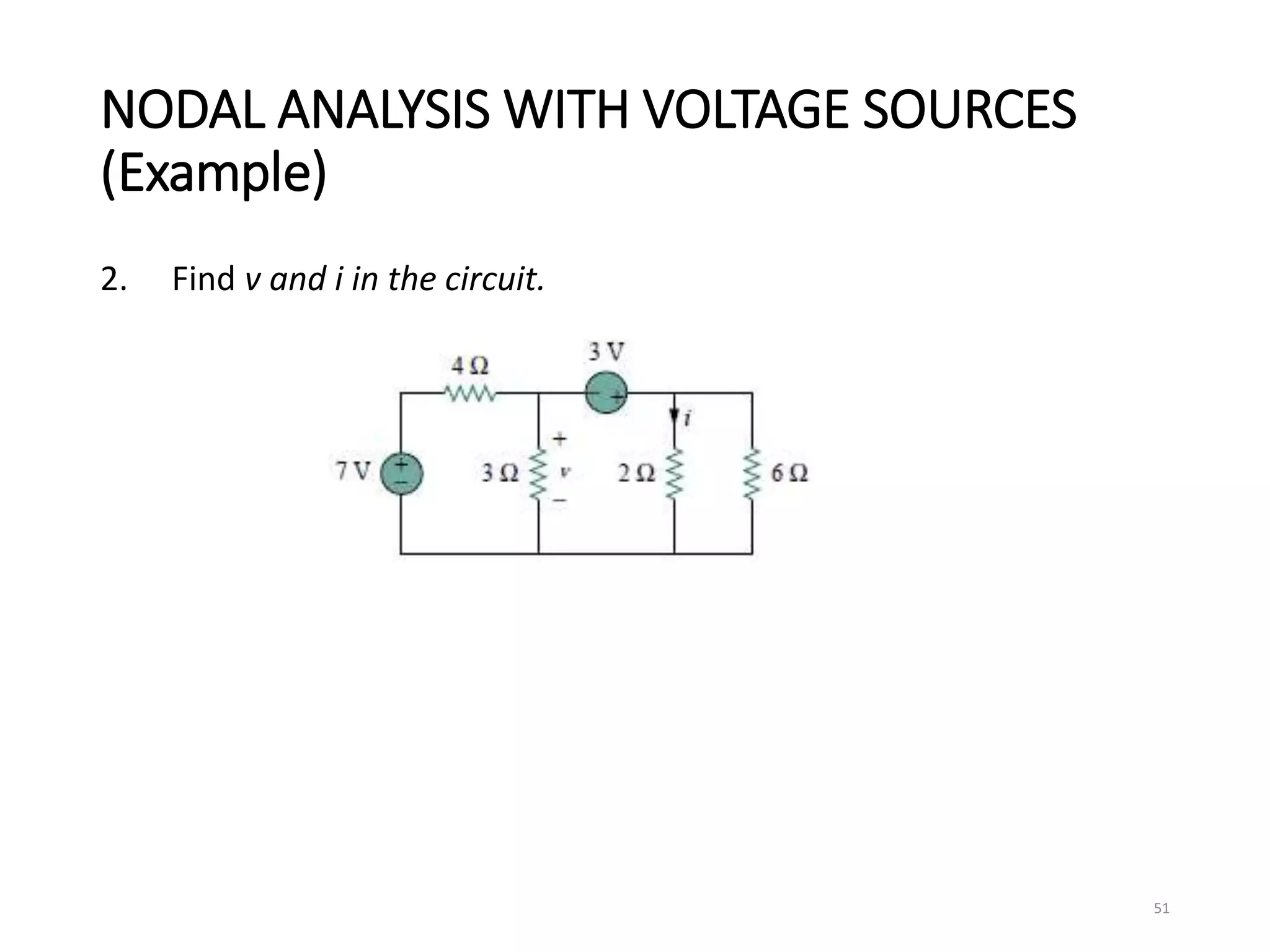
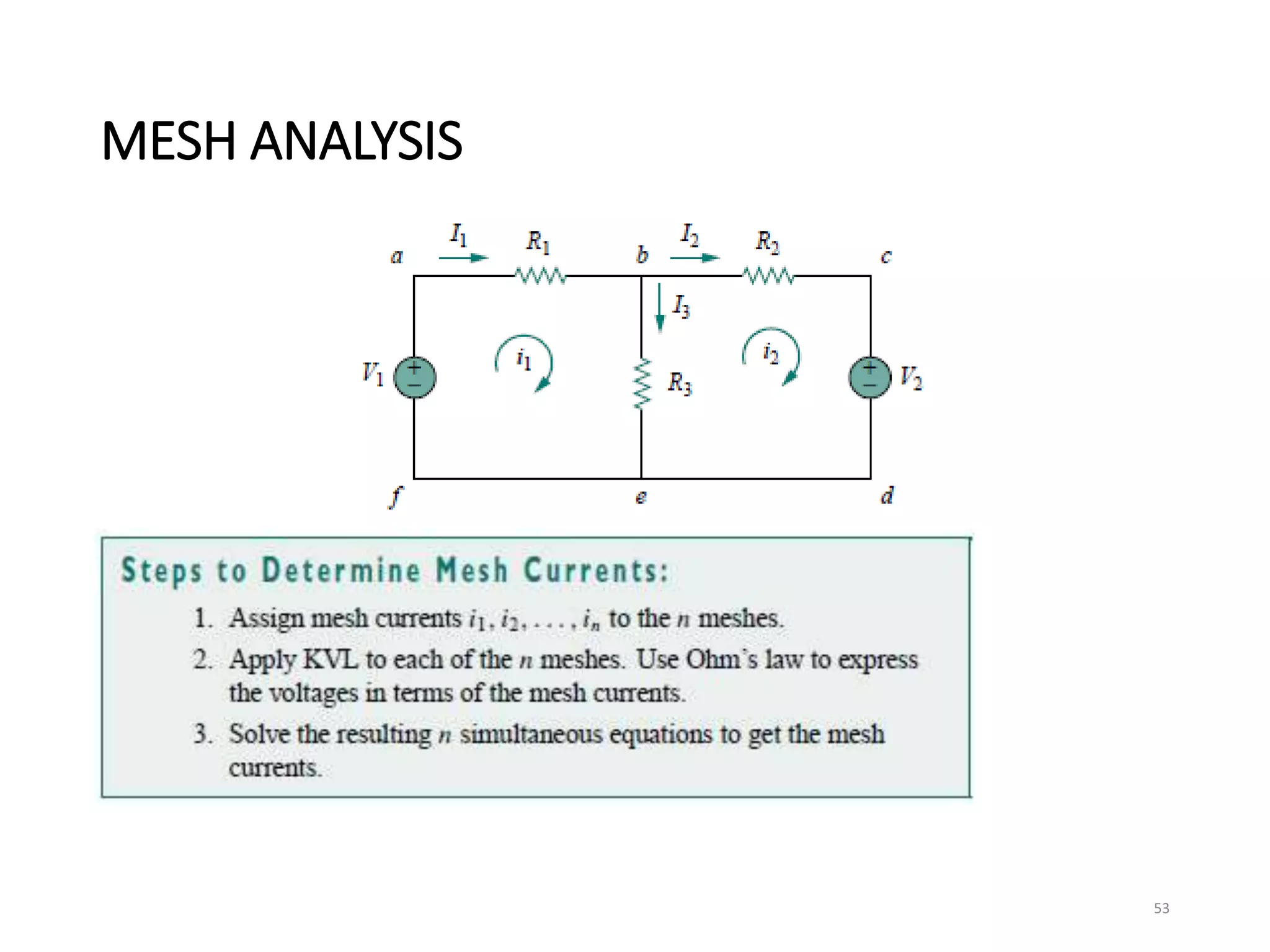
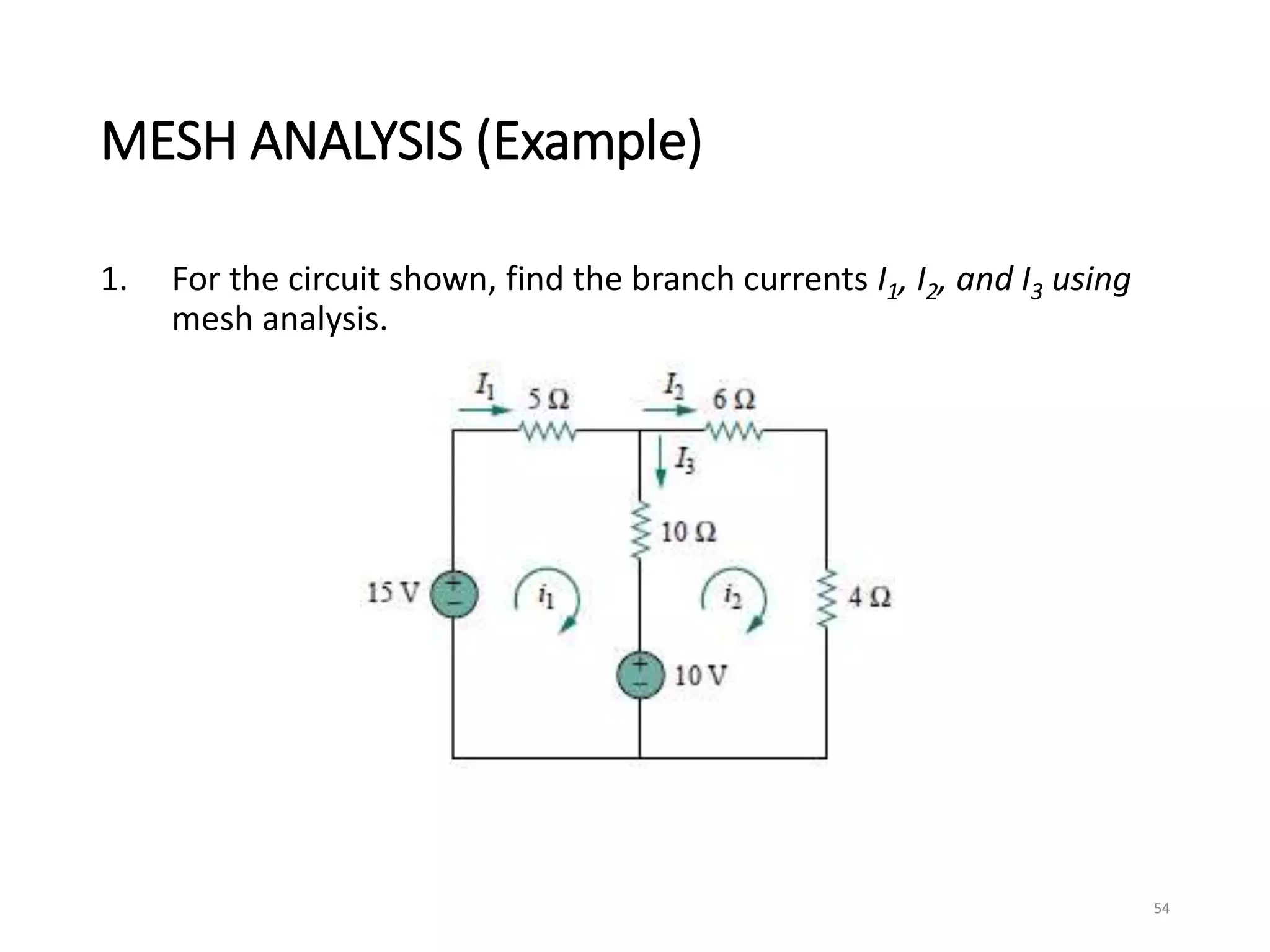
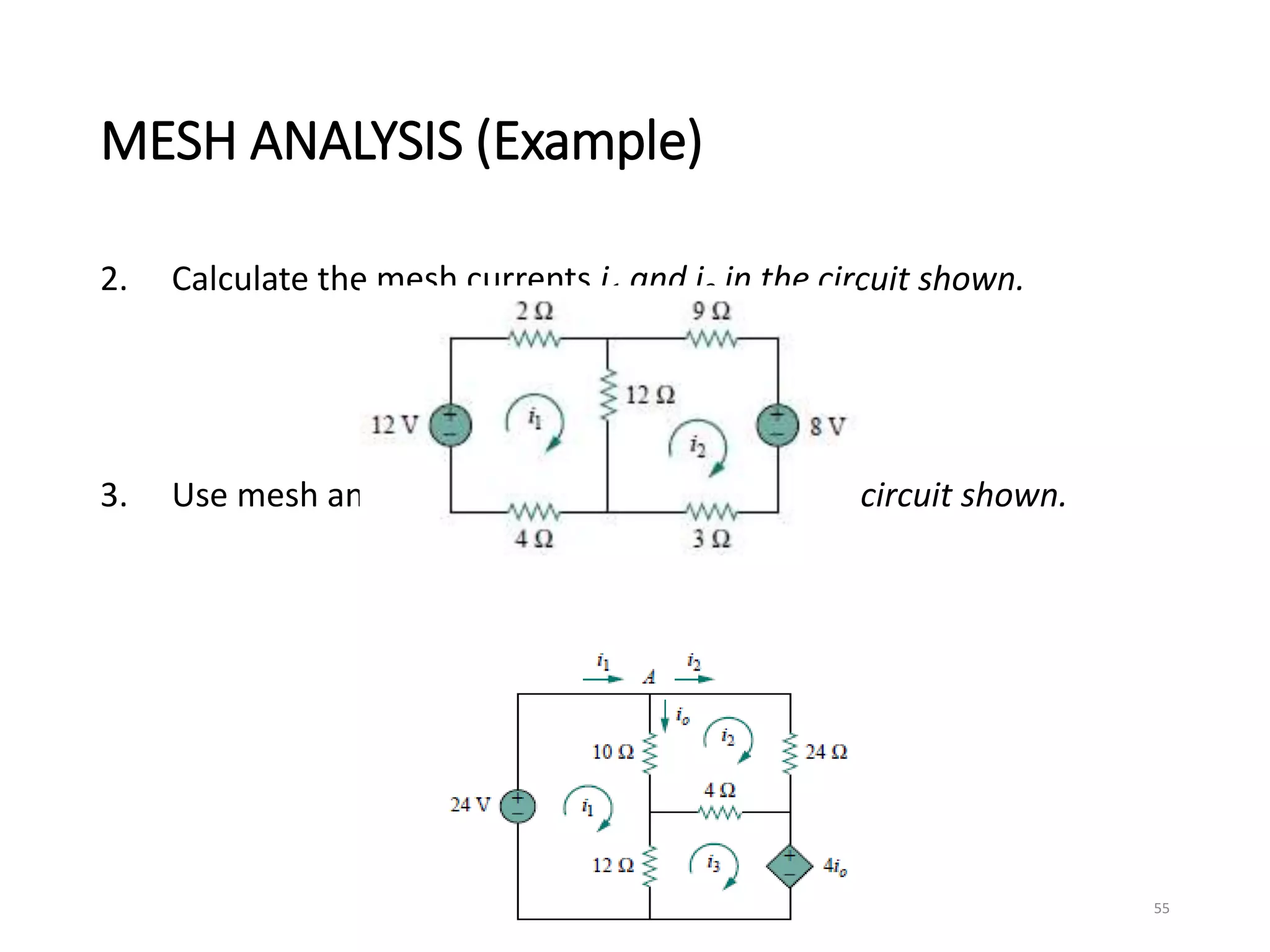
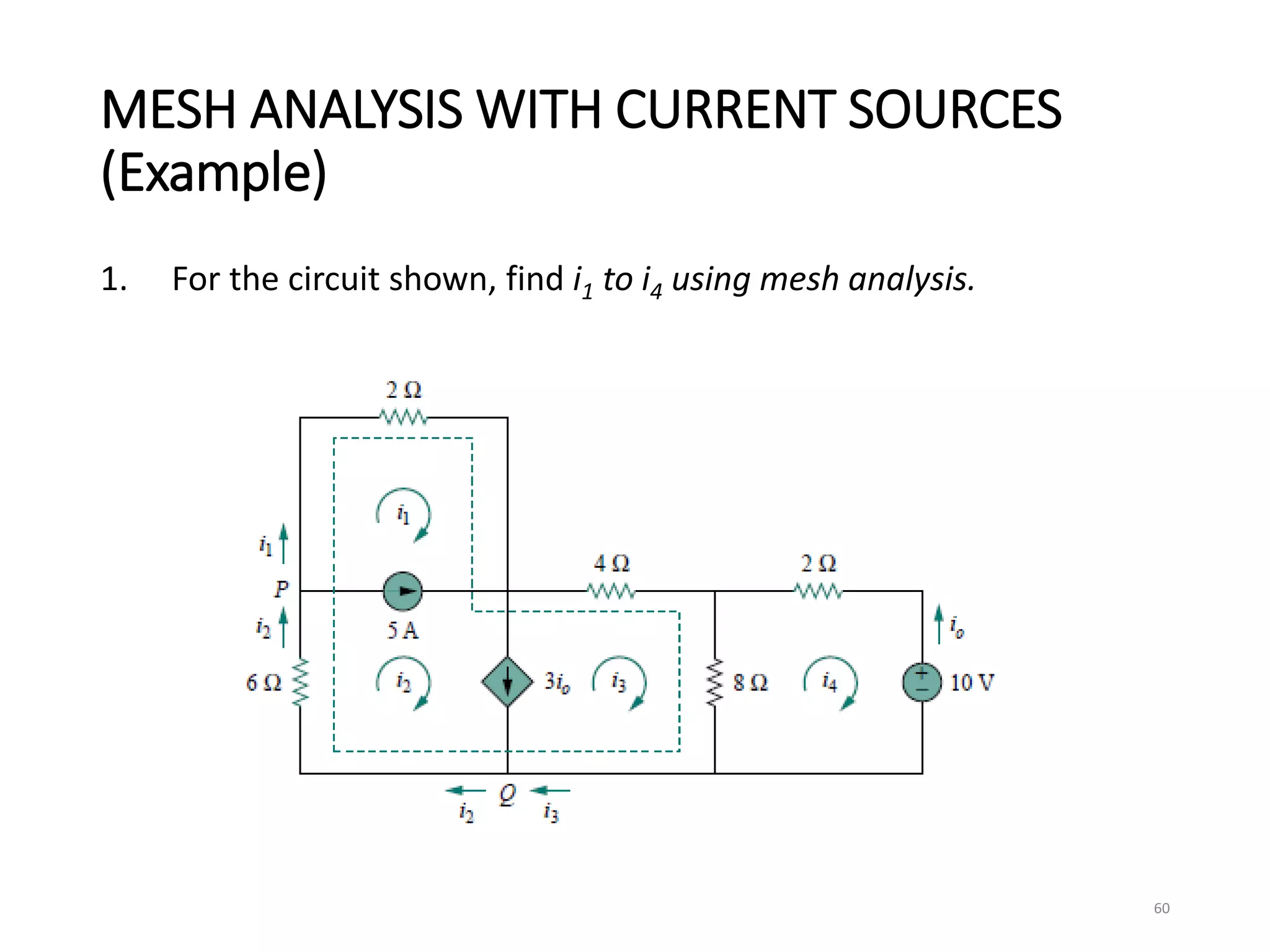
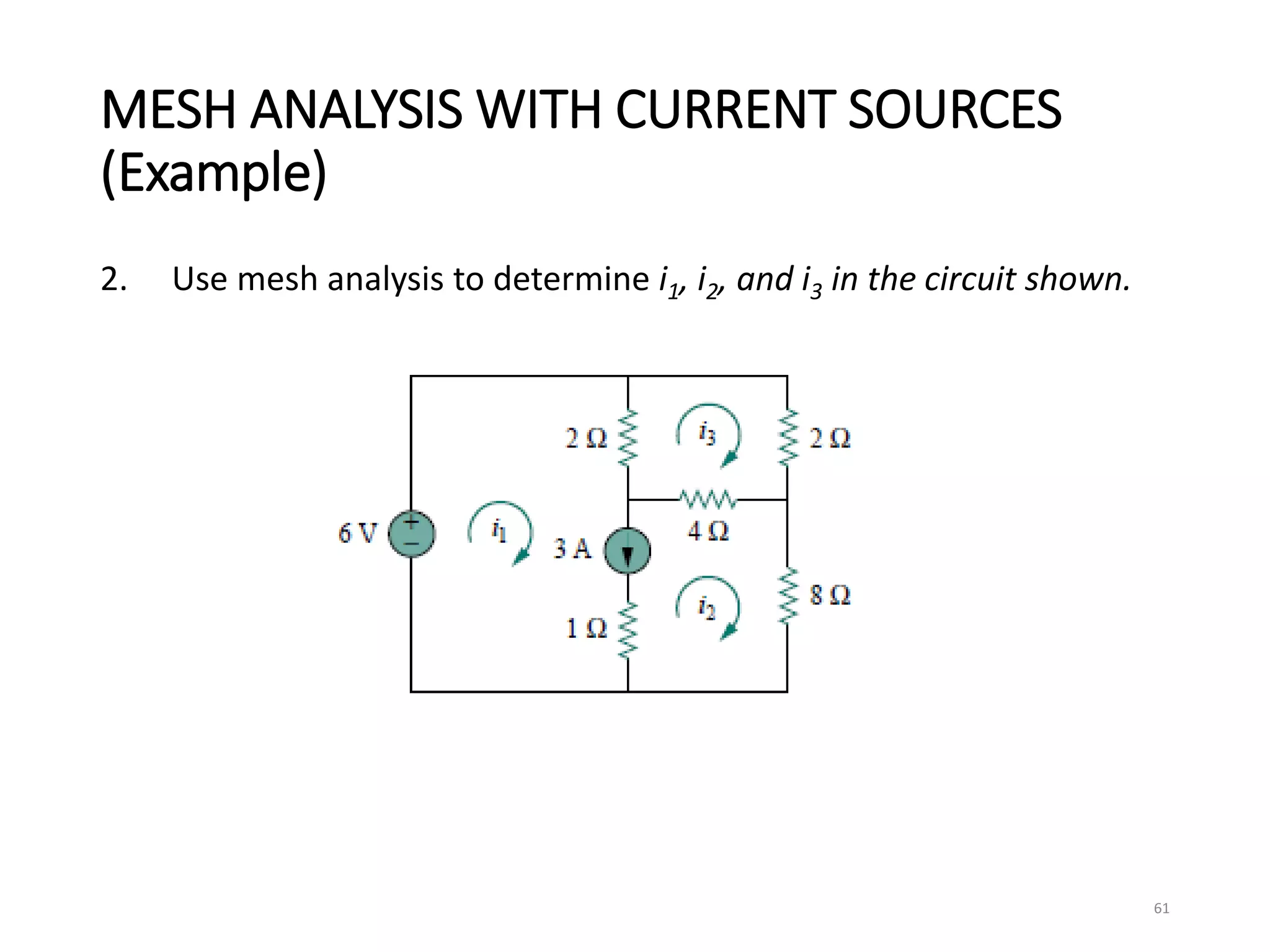
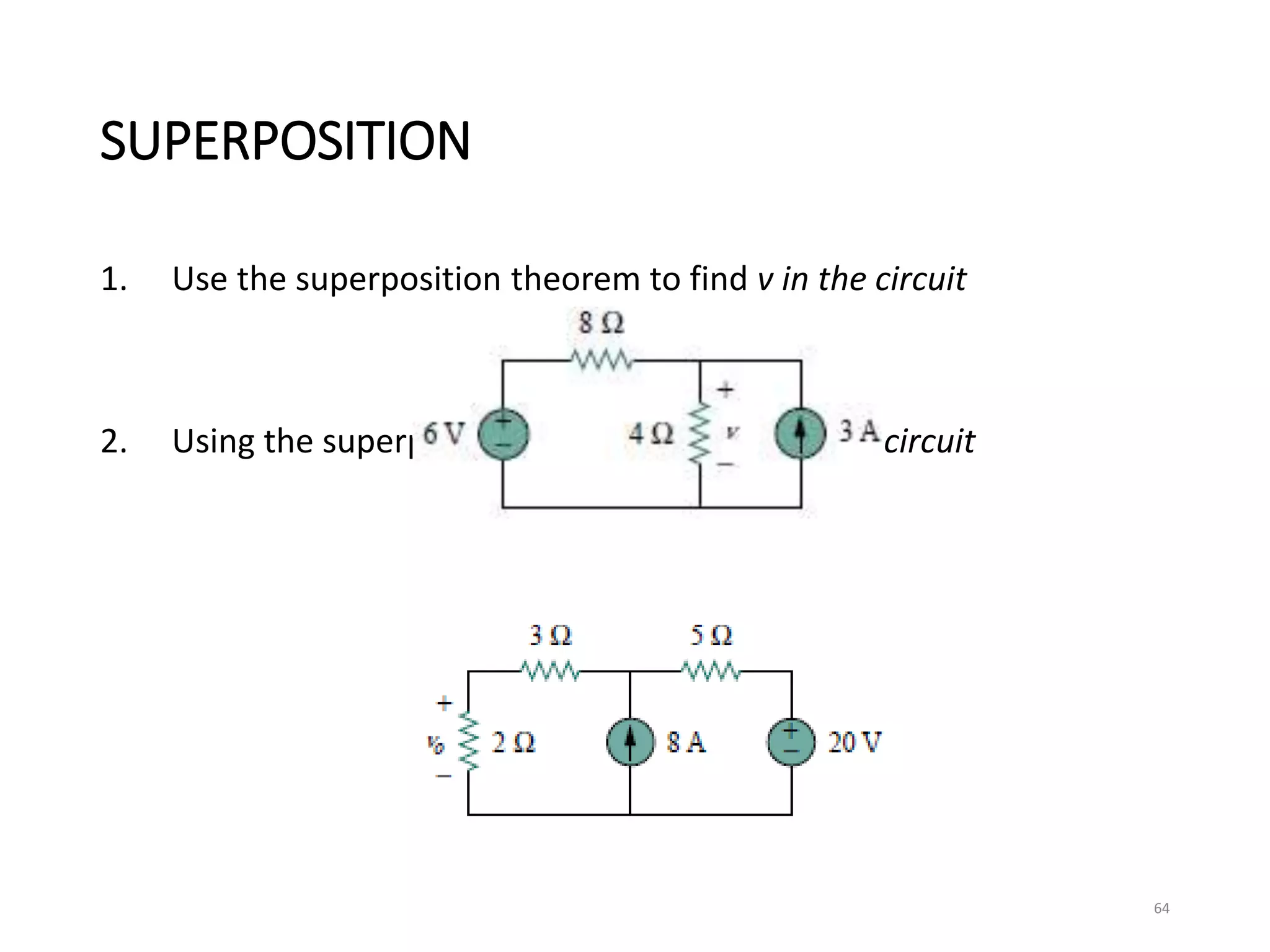
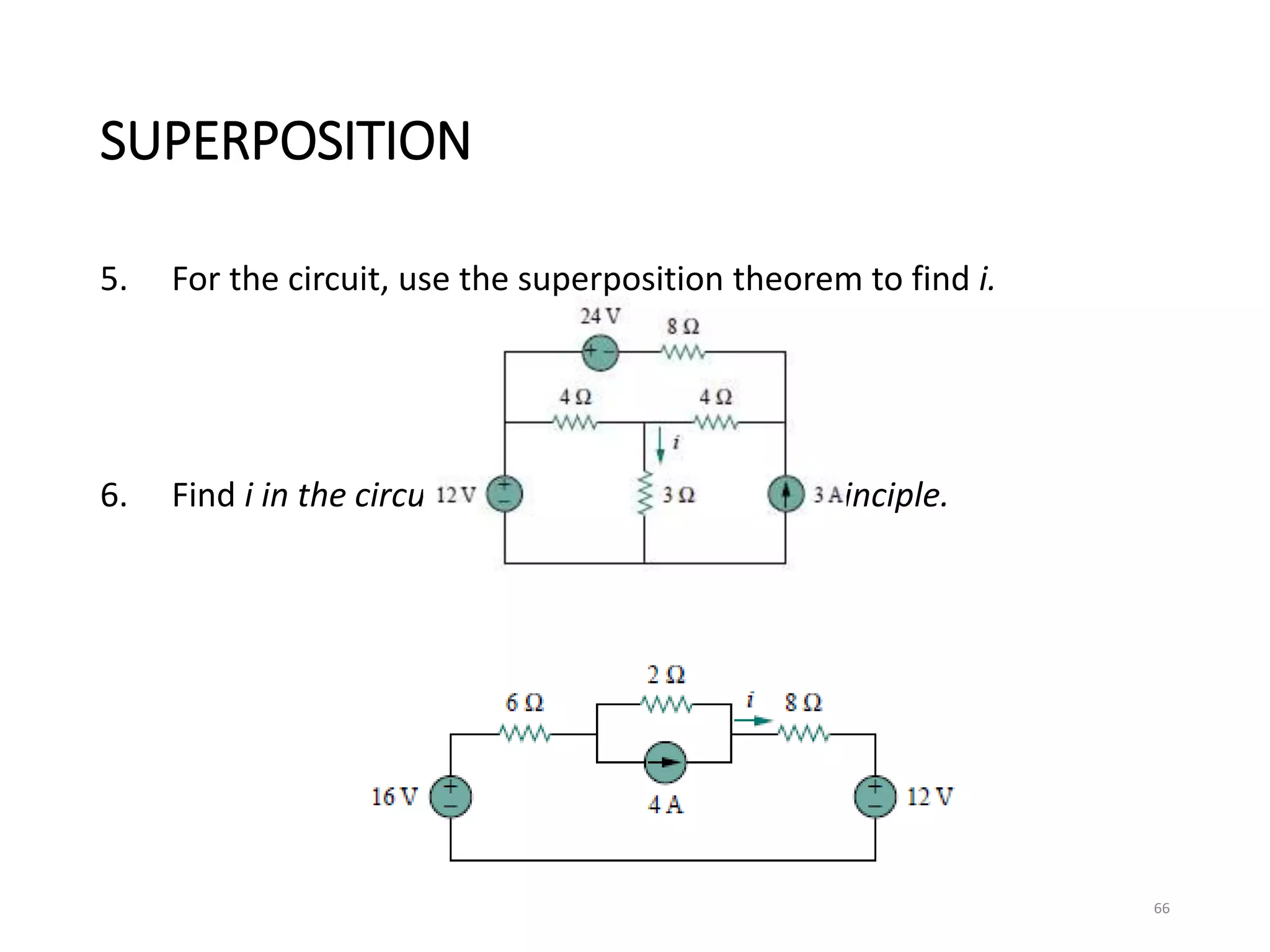
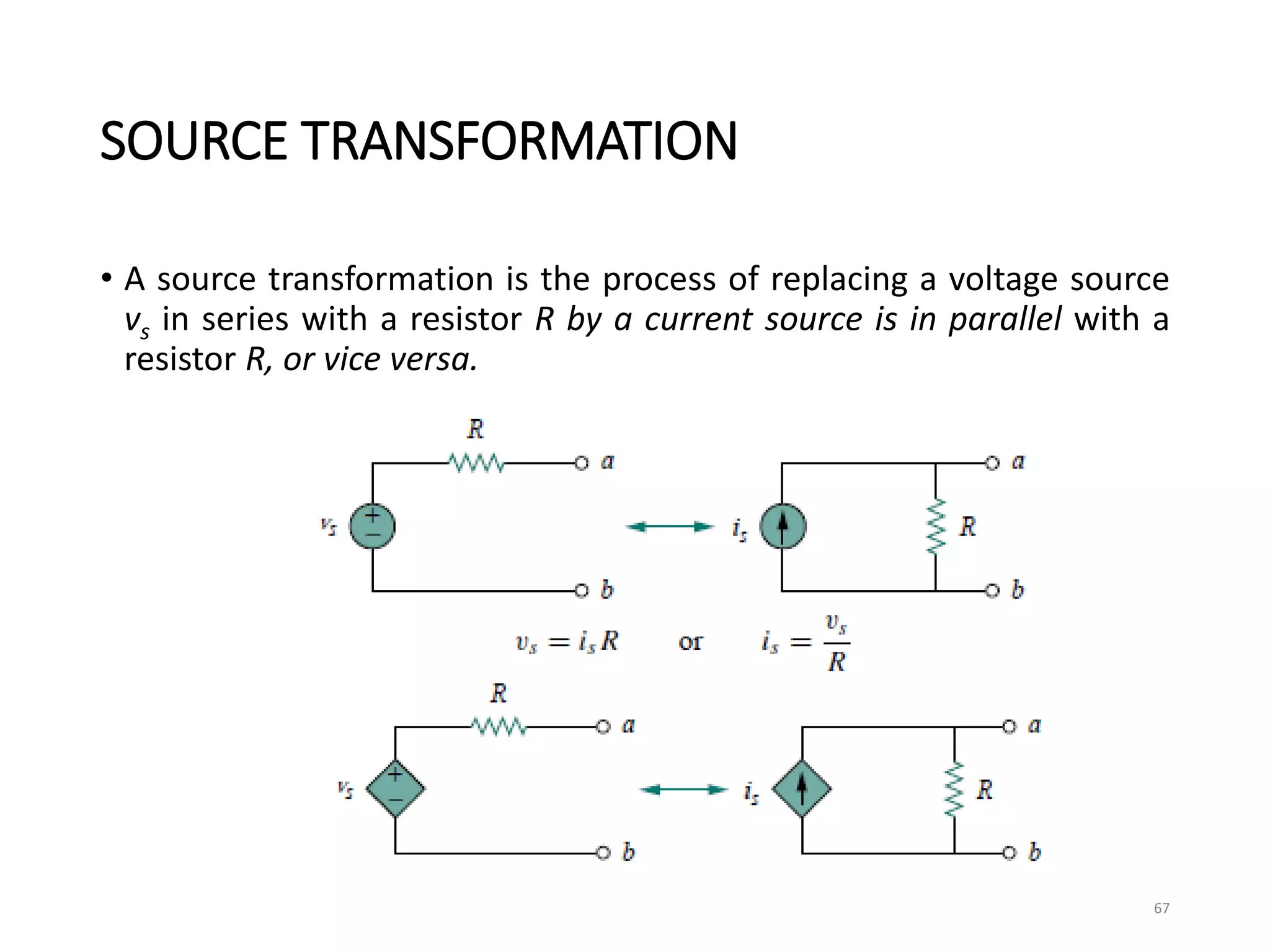
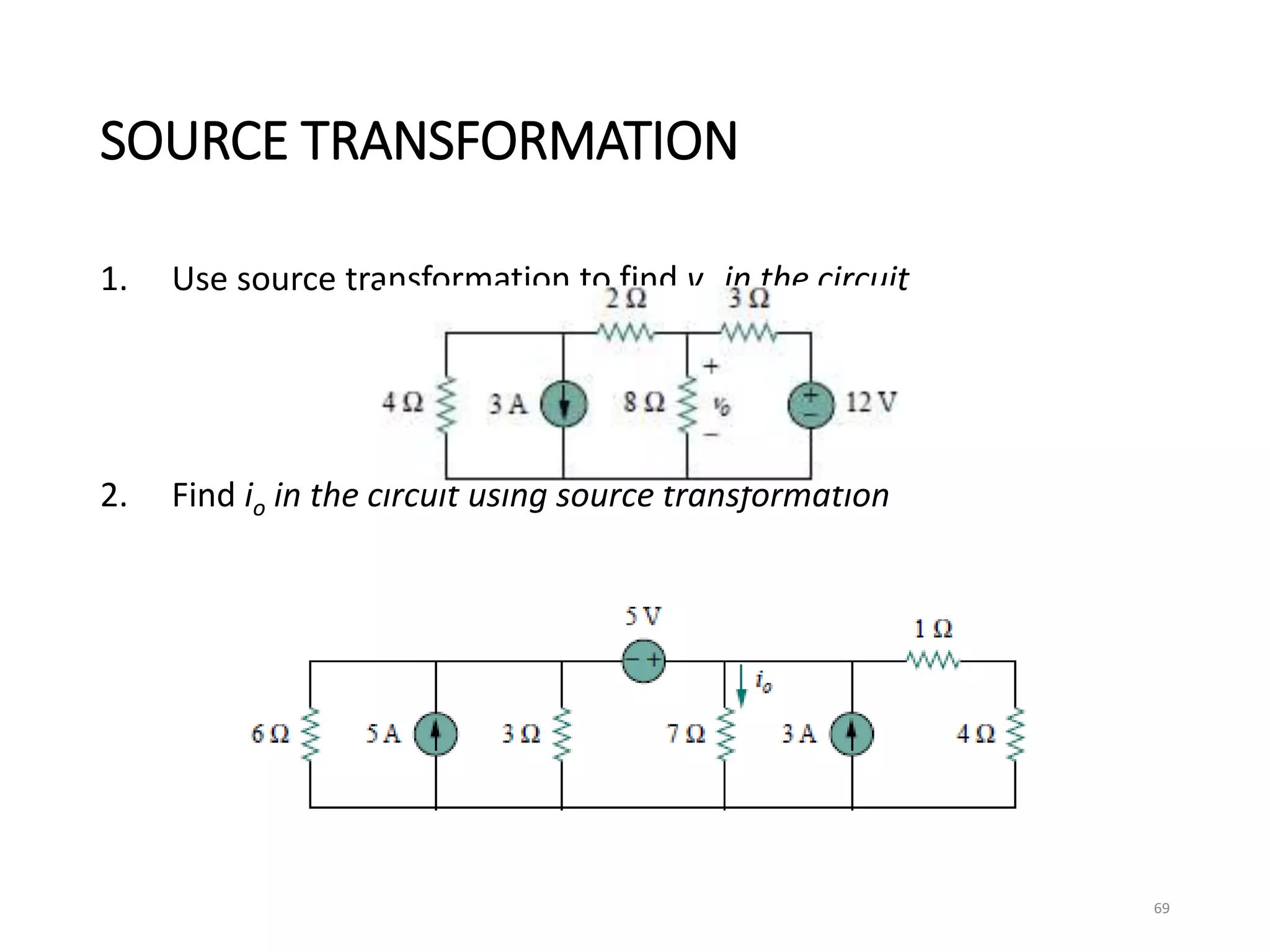
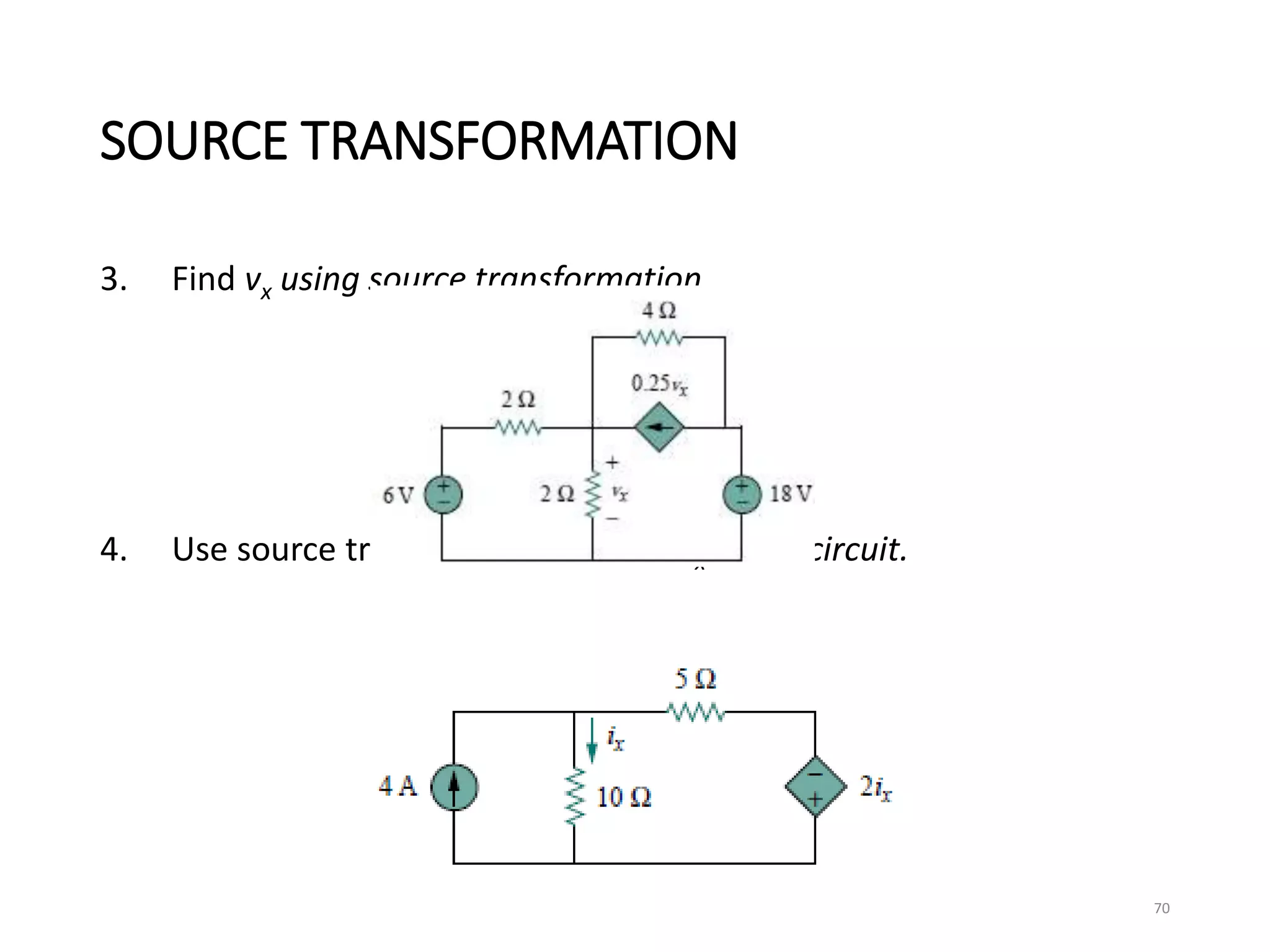
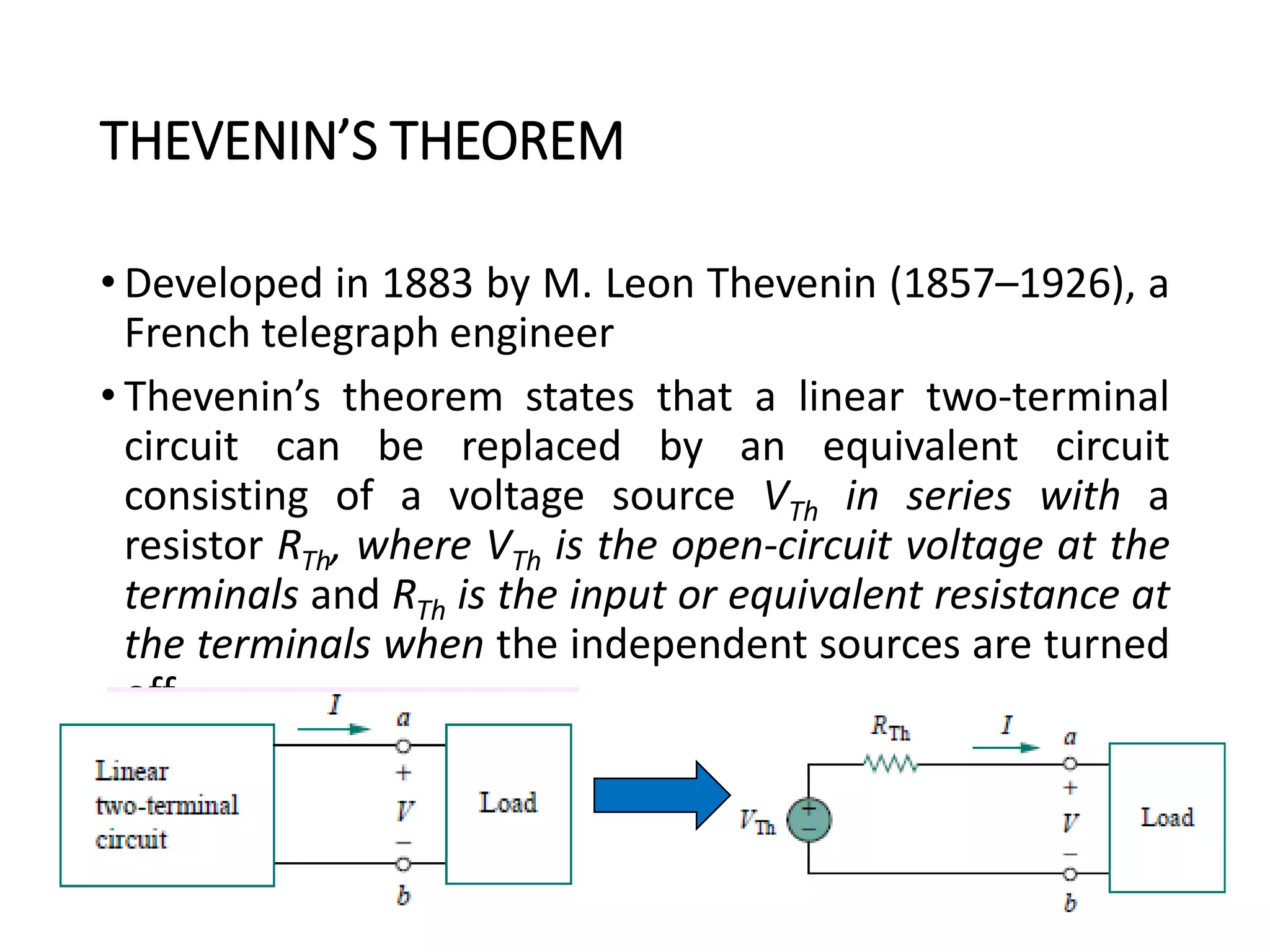
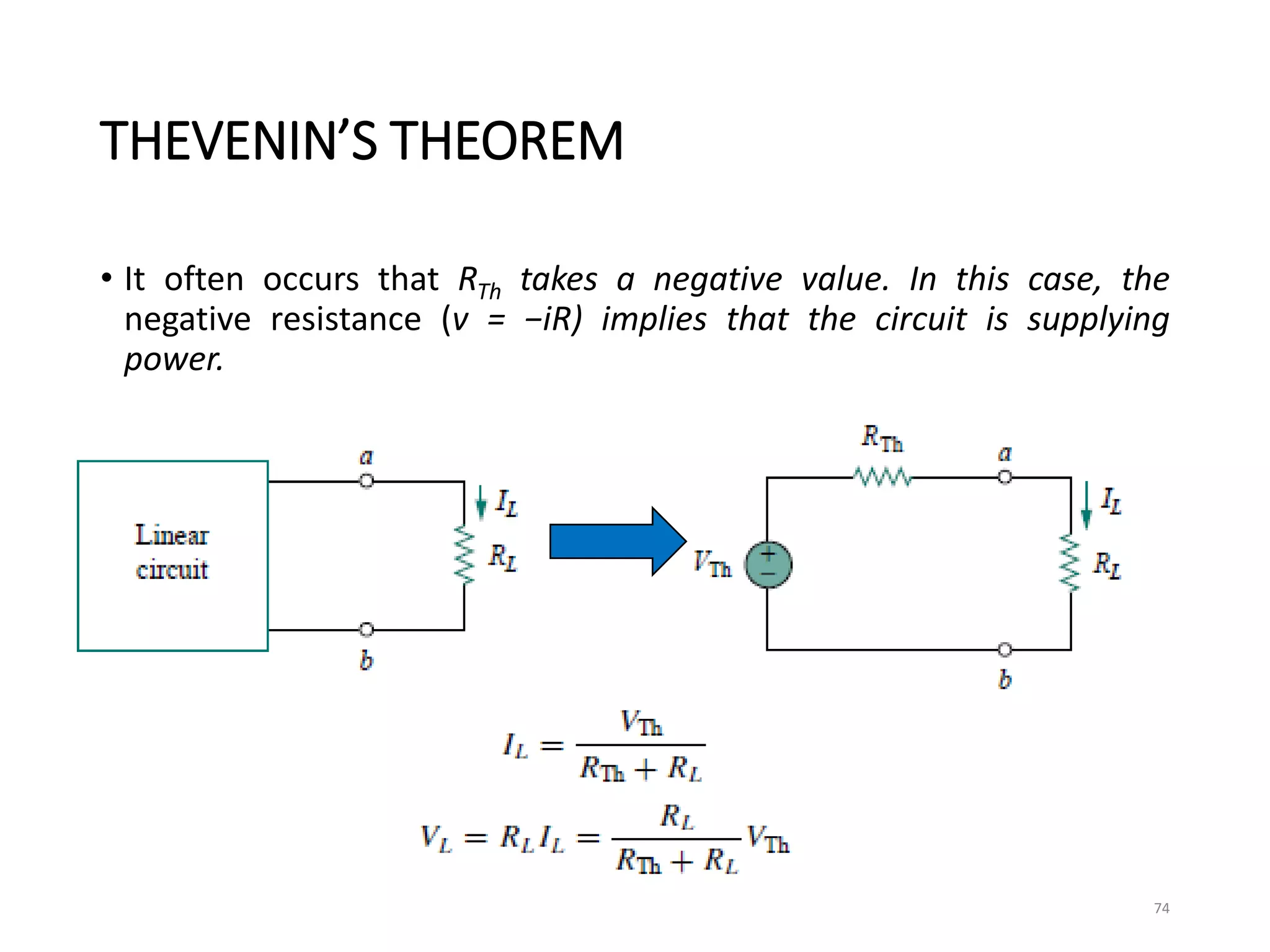
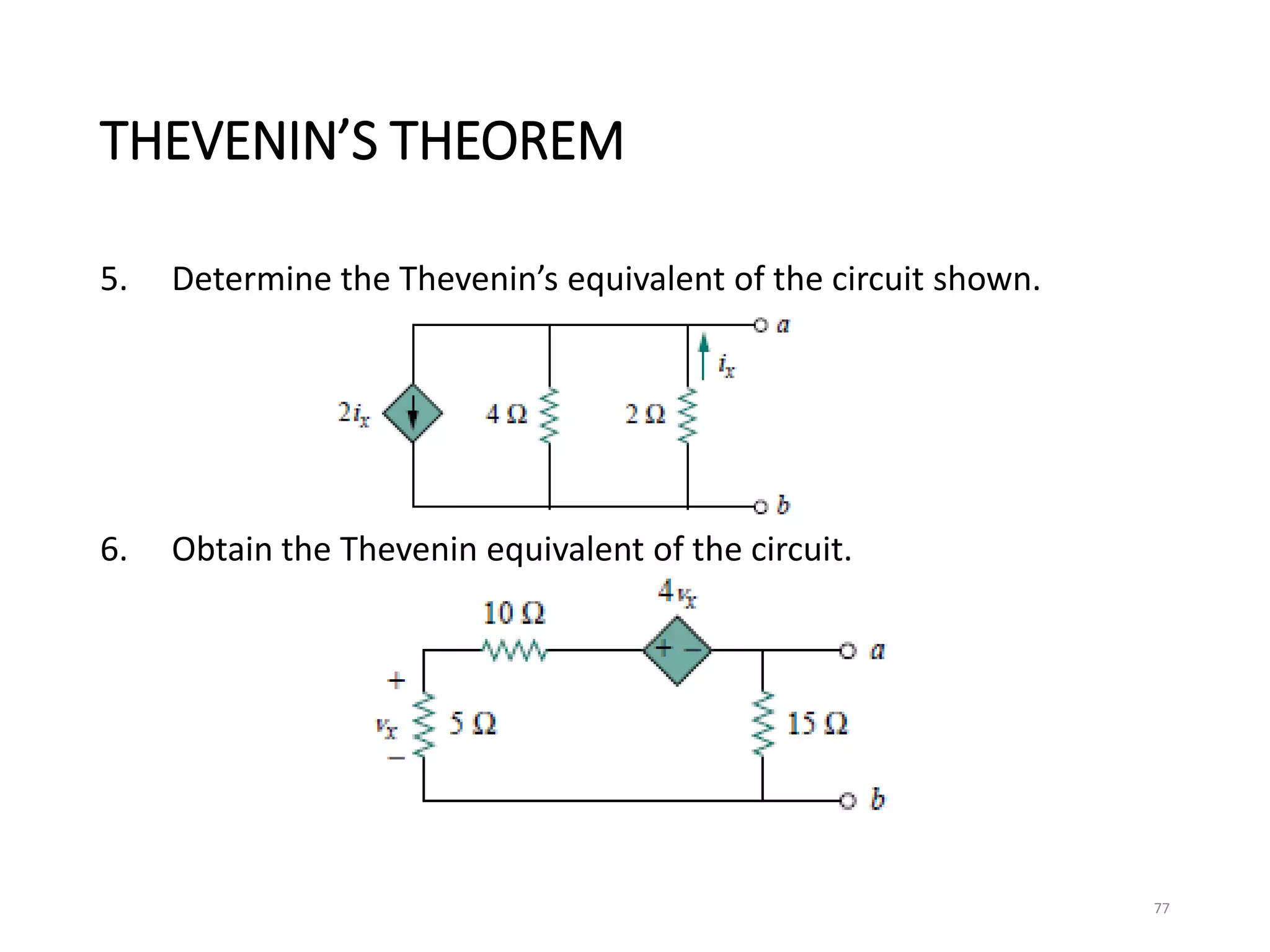
The document provides an extensive overview of electrical circuit analysis, covering key concepts such as charge, current, voltage, power, energy, circuit elements, and laws governing circuits. It discusses foundational principles like Ohm's Law, Kirchhoff’s Laws, and methodologies like nodal and mesh analysis for system evaluation. Additionally, it introduces dependent and independent sources, and techniques for analyzing complex circuits like series and parallel configurations.

1. “Electrical Circuit Analysis”
BEEE (BE-104)
1
BY:
PROF. PRASANT KUMAR
DEPT. OF ELECTRICAL
ENGINEERING

2. CHARGE AND CURRENT
• Charge
• most basic quantity in an electric circuit
• is an electrical property of the atomic particles of which matter consists,
measured in coulombs (C).
• charge e on an electron is negative and equal in magnitude to 1.602×10−19 C,
while a proton carries a positive charge of the same magnitude as the
electron. The presence of equal numbers of protons and electrons leaves an
atom neutrally charged.
2

3. CHARGE AND CURRENT
• Points should be noted about electric charge:
• The coulomb is a large unit for charges. In 1 C of charge, there are 1/(1.602 ×
10−19) = 6.24 × 1018 electrons. Thus realistic or laboratory values of charges
are on the order of pC, nC, or μC.
• According to experimental observations, the only charges that occur in nature
are integral multiples of the electronic charge e = −1.602 × 10−19 C.
• The law of conservation of charge states that charge can neither be created
nor destroyed, only transferred. Thus the algebraic sum of the electric charges
in a system does not change.
3

4. CHARGE AND CURRENT
• Electric charge or electricity is mobile
4
• Positive charges move in one
direction while negative charges
move in the opposite direction
• Motion of charges creates
electric current
• Conventionally take the
current flow as the movement of
positive charges, that is,
opposite to the flow of negative
charges.

5. CHARGE AND CURRENT
• Electric current is the time rate of change of charge, measured in amperes
(A).
•Direct Current (DC) is a current that remains constant
with time.
•Alternating Current (AC) is a current that varies
sinusoidally with time.
5
1 ampere = 1 coulomb/second

6. VOLTAGE
• Voltage (or potential difference) is the energy required to move a
unit charge through an element, measured in volts (V).
• Voltage vab between two points a and b in an electric circuit is the
energy (or work) needed to move a unit charge from a to b;
mathematically,
• where w is energy in joules (J) and q is charge in coulombs (C).
• Voltage vab or simply v is measured in volts (V)
6
1 volt = 1 joule/coulomb = 1 newton meter/coulomb

7. VOLTAGE
• The plus (+) and minus (−) signs are used to define reference direction
or voltage polarity.
7
(1) point a is at a potential of vab volts higher than point b
(2) the potential at point a with respect to point b is vab
vab = −vba
(a), there is a 9-V voltage drop from a to b
or equivalently a 9-V voltage rise from b to
a.
(b), point b is −9 V above point a.
A voltage drop from a to b is equivalent to
a voltage rise from b to a.
constant voltage is called a dc voltage and is represented by V, whereas a
sinusoidally time-varying voltage is called an ac voltage and is represented by

8. POWER AND ENERGY
• Power is the time rate of expending or absorbing energy, measured in
watts (W).
• where p is power in watts (W), w is energy in joules (J), and t is time in seconds
(s).
• power p is a time-varying quantity and is called the instantaneous power.
• If the power has a + sign, power is being delivered to or absorbed by
the element. If, on the other hand, the power has a − sign, power is being
supplied by the element.
8

9. POWER AND ENERGY
• Passive sign convention is satisfied when the current enters through
the positive terminal of an element and p = +vi. If the current enters
through the negative terminal, p = −vi.
9

10. POWER AND ENERGY
• law of conservation of energy must be obeyed:
• algebraic sum of power in a circuit, at any instant of time, must be zero.
• Energy absorbed or supplied by an element from time t0 to time t is
• Energy is the capacity to do work, measured in joules ( J).
• electric power utility companies measure energy in watt-hours (Wh)
10

11. CIRCUIT ELEMENTS
• Two types of elements found in electric circuits:
• Passive element – not capable of generating energy (resistors, capacitors, and
inductors)
• Active element - capable of generating energy (generators, batteries, and
operational amplifiers)
• Two kinds of sources:
• Independent Sources - an active element that provides a specified voltage or
current that is completely independent of other circuit variables
• Dependent Sources - an active element in which the source quantity is
controlled by another voltage or current. (transistors, operational amplifiers and
integrated circuits)
11

12. CIRCUIT ELEMENTS
• Ideal Independent Voltage Source delivers to the circuit whatever
current is necessary to maintain its terminal voltage (batteries and
generators).
• Symbols for independent voltage sources: (a) used for constant or time-varying
voltage, (b) used for constant voltage (dc).
12

13. CIRCUIT ELEMENTS
• Ideal Independent Current Source is an active element that provides
a specified current completely independent of the voltage across the
source.
• Symbol for independent current source
13

14. CIRCUIT ELEMENTS
• Four possible types of dependent sources:
• Voltage-Controlled Voltage Source (VCVS).
• Current-Controlled Voltage Source (CCVS).
• Voltage-Controlled Current Source (VCCS).
• Current-Controlled Current Source (CCCS).
• Symbols for: (a) dependent voltage source, (b) dependent current source.
14

15. CIRCUIT ELEMENTS
1. Calculate the power supplied or absorbed by each element
2. Compute the power absorbed or supplied by each component of
the circuit
15

16. OHM’S LAW
• Resistance (R) –of an element denotes its ability to resist the flow of
electric current; it is measured in ohms (Ω).
• The resistance of any material with a uniform cross-sectional area (A)
depends on A and its length (l)
• where ρ is known as the resistivity of the material in ohm-meters.
• Good conductors, such as copper and aluminum, have low resistivities,
while insulators, such as mica and paper, have high resistivities.
16

17. OHM’S LAW
17
(a) Resistor, (b) Circuit symbol
for resistance.

18. OHM’S LAW
• Ohm’s law states that the voltage “v” across a resistor is directly
proportional to the current “i” flowing through the resistor.
• Short circuit is a circuit element with resistance approaching zero.
• Open circuit is a circuit element with resistance approaching infinity.
18

19. OHM’S LAW
• (a) Short circuit (R = 0), (b) Open circuit (R =∞).
19

20. OHM’S LAW
• Conductance is the ability of an element to conduct electric current; it is
measured in mhos ( ) or siemens (S).
• Resistance can be expressed in ohms or siemens
• The power dissipated by a resistor can be expressed in terms of R.
• The power dissipated by a resistor may also be expressed in terms of G
20

21. OHM’S LAW
1. An electric iron draws 2 A at 120 V. Find its resistance.
2. In the circuit shown, calculate the current i, the conductance G, and the
power p.
3. A voltage source of 20 sin πt V is connected across a 5-k resistor. Find
the current through the resistor and the power dissipated.
21

22. NODES, BRANCHES, AND LOOPS
• A branch represents a single element such as a voltage source or a
resistor
• A node is the point of connection between two or more branches
• A loop is any closed path in a circuit.
• A network with b branches, n nodes, and l independent loops will
satisfy the fundamental theorem of network topology:
b = l + n − 1
22

23. NODES, BRANCHES, AND LOOPS
• Two or more elements are in series if they are cascaded or connected
sequentially and consequently carry the same current
• Two or more elements are in parallel if they are connected to the
same two nodes and consequently have the same voltage across
them.
23

24. NODES, BRANCHES, AND LOOPS
1. Determine the number of branches and nodes in the circuit
shown. Identify which elements are in series and which are in
parallel.
2. How many branches and nodes does the circuit in have? Identify
the elements that are in series and in parallel.
24

25. KIRCHHOFF’S LAWS
• Kirchhoff’s current law (KCL) states that the algebraic sum of
currents entering a node (or a closed boundary) is zero.
• where N is the number of branches connected to the node and in is
the nth current entering (or leaving) the node. By this law, currents
enteringa node may be regarded as positive, while currents leaving
the node maybe taken as negative or vice versa.
25

26. KIRCHHOFF’S LAWS
• The sum of the currents entering a node is equal to the sum of the
currents leaving the node.
26

27. KIRCHHOFF’S LAWS
• Kirchhoff’s voltage law (KVL) states that the algebraic sum of all
voltages around a closed path(or loop) is zero.
• where M is the number of voltages in the loop (or the number of
branches in the loop) and vm is the mth voltage.
27

28. KIRCHHOFF’S LAWS
• By KVL:
−v1 + v2 + v3 − v4 + v5 = 0
v2 + v3 + v5 = v1 + v4
• Sum of voltage drops = Sum of voltage rises
28

29. KIRCHHOFF’S LAWS
1. For the circuit, find voltages v1 and v2.
2. Determine vo and i in the circuit shown.
29

30. KIRCHHOFF’S LAWS
3. Find current io and voltage vo in the circuit shown
4. Find the currents and voltages in the circuit shown
30

31. SERIES RESISTORS AND VOLTAGE DIVISION
• Using Ohms Law
• By KVL (clockwise direction)
31
The equivalent resistance
of any number of resistors
connected in series is the
sum of the individual
resistances.

32. SERIES RESISTORS AND VOLTAGE DIVISION
• Voltage across each resistor
• Principle of Voltage Division - source voltage ‘v’ is divided among the
resistors in direct proportion to their resistances; the larger the
resistance, the larger the voltage drop.
32

33. PARALLEL RESISTORS AND CURRENT DIVISION
• By Ohms Law
• By KCL @ Node ‘a’
• Then:
33

34. PARALLEL RESISTORS AND CURRENT DIVISION
• Where:
34
The equivalent resistance of two
parallel resistors is equal to the
product of their resistances divided
by their sum.
Req is always smaller than the
resistance of the smallest resistor in the
parallel combination. If R1 = R2 = … = RN
= R, then

35. PARALLEL RESISTORS AND CURRENT DIVISION
• Equivalent conductance for N resistors in parallel :
• The equivalent conductance of resistors connected in parallel is the sum of
their individual conductance's.
• Equivalent conductance Geq of N resistors in series:
35

36. PARALLEL RESISTORS AND CURRENT DIVISION
• Principle of Current Division - total current ‘i’ is shared by the resistors
in inverse proportion to their resistances.
36

37. Example
1. Find Req for the circuit shown in Fig. A.
2. Calculate the equivalent resistance Rab in the circuit shown in Fig.
B
3. Find the equivalent conductance Geq for the circuit in Fig. C.
37
Fig. A
Fig. B
Fig. C

38. Example
4. Find io and vo in the circuit shown in Fig. D. Calculate the power
dissipated in the 3- resistor.
5. For the circuit shown in Fig. E, determine: (a) the voltage vo,
(b)the power supplied by the current source, (c) the power
absorbed by each resistor.
38
Fig. D
Fig. E

39. WYE-DELTA TRANSFORMATIONS
39
The bridge
network
Two forms of the same network: (a) Y, (b) T.
Two forms of the same network: (a) Δ, (b) π.

40. WYE-DELTA TRANSFORMATIONS
• Delta to Wye Conversion
• Each resistor in the Y network is the product of the resistors in the
two adjacent Δ branches, divided by the sum of the three Δ resistors.
40

41. WYE-DELTA TRANSFORMATIONS
• Wye to Delta Conversion
• Each resistor in the Δ network is the sum of all possible products of Y
resistors taken two at a time, divided by the opposite Y resistor.
41

42. WYE-DELTA TRANSFORMATIONS
• The Y and Δ networks are said to be balanced when
• Under these conditions, conversion formulas become
42

43. Example
1. Convert the Δ network in Fig. A to an equivalent Y network.
2. Obtain the equivalent resistance Rab for the circuit in Fig. B and
use it to find current ‘i’.
43
Fig. A Fig. B

44. NODAL ANALYSIS
• Nodal analysis provides a general procedure for analyzing circuits using node
voltages as the circuit variables
• Steps to Determine Node Voltages:
1. Select a node as the reference node. Assign voltages v1, v2, . . . , vn−1 to the
remaining n − 1 nodes. The voltages are referenced with respect to the reference
node.
2. Apply KCL to each of the n − 1 nonreference nodes. Use Ohm’s law to express the
branch currents in terms of node voltages.
3. Solve the resulting simultaneous equations to obtain the unknown node voltages.
44

45. NODAL ANALYSIS
• Current flows from a higher potential to a lower potential in a resistor.
45

46. NODAL ANALYSIS
• @ Node 1
• @ Node 2
• Then;
• So;
46
In Terms of Conductance:
In Matrix Form:

47. NODAL ANALYSIS (Example)
1. Calculate the node voltages in the circuits shown.
47

48. NODAL ANALYSIS WITH VOLTAGE SOURCES
• Case 1: If a voltage source is connected between the reference node
and a nonreference node, we simply set the voltage at the
nonreference node equal to the voltage of the voltage source.
• Case 2: If the voltage source (dependent or independent) is
connected between two nonreference nodes, the two nonreference
nodes form a generalized node or supernode; we apply both KCL and
KVL to determine the node voltages.
48

49. NODAL ANALYSIS WITH VOLTAGE SOURCES
• A supernode is formed by
enclosing a (dependent or
independent) voltage source
connected between two
nonreference nodes and any
elements connected in parallel
with it.
49
Note the following properties of a supernode:
1. The voltage source inside the supernode provides a
constraint equation needed to solve for the node voltages.
2. A supernode has no voltage of its own.
3. A supernode requires the application of both KCL and KVL.

50. NODAL ANALYSIS WITH VOLTAGE SOURCES
(Example)
1. For the circuits shown, find the node voltages.
50

51. NODAL ANALYSIS WITH VOLTAGE SOURCES
(Example)
2. Find v and i in the circuit.
51

52. MESH ANALYSIS
• Mesh analysis provides another general procedure for analyzing circuits,
using mesh currents as the circuit variables
• A mesh is a loop that does not contain any other loop within it
• Nodal analysis applies KCL to find unknown voltages in a given circuit, while
mesh analysis applies KVL to find unknown currents
• only applicable to a circuit that is planar
• Planar circuit is one that can be drawn in a plane with no branches crossing
one another; otherwise it is nonplanar.
52

53. MESH ANALYSIS
53

54. MESH ANALYSIS (Example)
1. For the circuit shown, find the branch currents I1, I2, and I3 using
mesh analysis.
54

55. MESH ANALYSIS (Example)
2. Calculate the mesh currents i1 and i2 in the circuit shown.
3. Use mesh analysis to find the current io in the circuit shown.
55

56. MESH ANALYSIS (Example)
4. Using mesh analysis, find io in the circuit shown.
56

57. MESH ANALYSIS WITH CURRENT SOURCES
• Case 1: When a current source exists only in one mesh:
• Case 2: When a current source exists between two meshes: We
create a supermesh by excluding the current source and any
elements connected in series with it.
57
Set i2 = −5 A and write a mesh
equation for the other mesh in the
usual way, that is,

58. MESH ANALYSIS WITH CURRENT SOURCES
• A supermesh results when two meshes have a (dependent or
independent) current source in common.
(a) Two meshes having a current source in common
(b) a supermesh, created by excluding the current source.
58

59. MESH ANALYSIS WITH CURRENT SOURCES
• Note the following properties of a supermesh:
1. The current source in the supermesh is not completely ignored; it
provides the constraint equation necessary to solve for the mesh
currents.
2. A supermesh has no current of its own.
3. A supermesh requires the application of both KVL and KCL.
59

60. MESH ANALYSIS WITH CURRENT SOURCES
(Example)
1. For the circuit shown, find i1 to i4 using mesh analysis.
60

61. MESH ANALYSIS WITH CURRENT SOURCES
(Example)
2. Use mesh analysis to determine i1, i2, and i3 in the circuit shown.
61

62. SUPERPOSITION
• The superposition principle states that the voltage across (or current
through) element in a linear circuit is the algebraic sum of the voltages
across (or currents through) that element due to each independent
source acting alone.
• To apply the superposition principle, we must keep two things in mind:
1. We consider one independent source at a time while all other independent
sources are turned off. This implies that we replace every voltage source by 0 V
(or a short circuit), and every current source by 0 A (or an open circuit). This
way we obtain a simpler and more manageable circuit.
2. Dependent sources are left intact because they are controlled by circuit
variables.
62

63. SUPERPOSITION
• Steps to Apply Superposition Principle :
• Turn off all independent sources except one source. Find the output (voltage
or current) due to that active source using nodal or mesh analysis.
• Repeat step 1 for each of the other independent sources.
• Find the total contribution by adding algebraically all the contributions due
to the independent sources.
63

64. SUPERPOSITION
1. Use the superposition theorem to find v in the circuit
2. Using the superposition theorem, find vo in the circuit
64

65. SUPERPOSITION
3. Find io in the circuit using superposition.
4. Use superposition to find vx in the circuit
65

66. SUPERPOSITION
5. For the circuit, use the superposition theorem to find i.
6. Find i in the circuit using the superposition principle.
66

67. SOURCE TRANSFORMATION
• A source transformation is the process of replacing a voltage source
vs in series with a resistor R by a current source is in parallel with a
resistor R, or vice versa.
67

68. SOURCE TRANSFORMATION
• Points to be mind when dealing with source transformation:
• The arrow of the current source is directed toward the positive terminal of the
voltage source.
• Source transformation is not possible when R = 0, which is the case with an ideal
voltage source. However, for a practical, nonideal voltage source, R = 0. Similarly,
an ideal current source with R =∞cannot be replaced by a finite voltage source.
68

69. SOURCE TRANSFORMATION
1. Use source transformation to find vo in the circuit
2. Find io in the circuit using source transformation
69

70. SOURCE TRANSFORMATION
3. Find vx using source transformation.
4. Use source transformation to find ix in the circuit.
70

71. THEVENIN’S THEOREM
• Developed in 1883 by M. Leon Thevenin (1857–1926), a
French telegraph engineer
• Thevenin’s theorem states that a linear two-terminal
circuit can be replaced by an equivalent circuit
consisting of a voltage source VTh in series with a
resistor RTh, where VTh is the open-circuit voltage at the
terminals and RTh is the input or equivalent resistance at
the terminals when the independent sources are turned
off.
71

72. THEVENIN’S THEOREM
• CASE 1: If the network has no dependent sources, we turn off all
independent sources. RTh is the input resistance of the network
looking between terminals a and b, as shown
72

73. THEVENIN’S THEOREM
• CASE 2: If the network has dependent sources, we turn off
all independent sources. As with superposition, dependent
sources are not to be turned off because they are controlled
by circuit variables. We apply a voltage source vo at
terminals a and b and determine the resulting current io.
Then RTh = vo/io, as shown. Alternatively, we may insert a
current source io at terminals a-b as shown in and find the
terminal voltage vo. Again RTh = vo/io. Either of the two
approaches will give the same result.
73

74. THEVENIN’S THEOREM
• It often occurs that RTh takes a negative value. In this case, the
negative resistance (v = −iR) implies that the circuit is supplying
power.
74

75. THEVENIN’S THEOREM
1. Find the Thevenin equivalent circuit of the circuit shown, to the left of
the terminals a-b. Then find the current through RL = 6Ω, 16Ω, and 36Ω
.
2. Using Thevenin’s theorem, find the equivalent circuit to the left of the
terminals in the circuit. Then find i.
75

76. THEVENIN’S THEOREM
3. Find the Thevenin equivalent of the circuit shown.
2. Find the Thevenin equivalent circuit of the circuit shown to the
left of the terminals.
76

77. THEVENIN’S THEOREM
5. Determine the Thevenin’s equivalent of the circuit shown.
6. Obtain the Thevenin equivalent of the circuit.
77

78. THANK
YOU
“I have no special talent. I am only
passionately curious”. By Albert Einstein