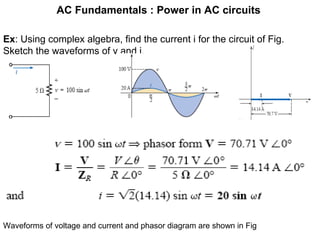
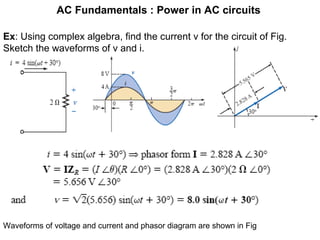
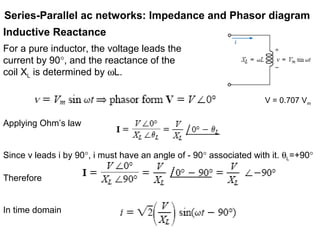
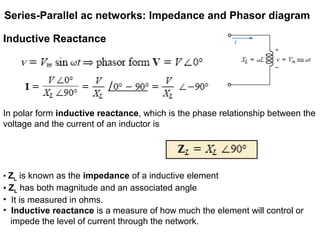
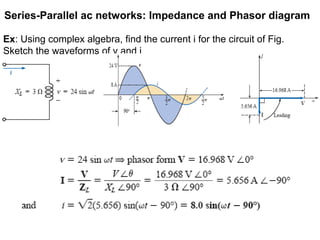
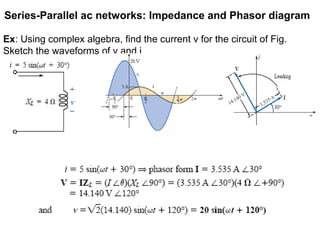
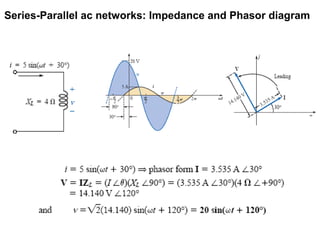
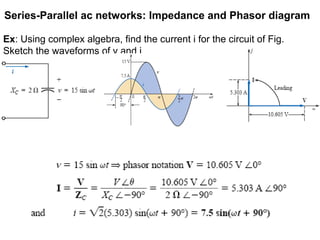
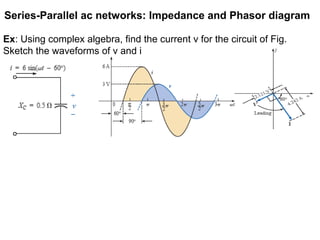
The document discusses series-parallel AC networks, focusing on impedance and phasor diagrams for resistive, inductive, and capacitive elements. It explains the phase relationships between voltage and current in these circuits, utilizing complex algebra for calculations. Additionally, it outlines how impedance affects current flow and describes the measurement units involved.

1. Series-Parallel
ac networks:
Impedance and
Phasor diagram

2. Series-Parallel ac networks: Impedance and Phasor diagram
Resistive elements
For the purely resistive circuit, the voltage and
Current are in phase and the magnitude is
In phasor form where
Applying Ohm’s law
since v and I are in phase
In time domain
V = 0.707 Vm

3. Series-Parallel ac networks: Impedance and Phasor diagram
Resistive elements
In polar form the phase relationship between the voltage and the current of a
resistor is
•
Phasor: A radius vector having a constant magnitude is called a phasor, when applied
to electric circuit.
Phasor diagram shows at a glance the magnitude and phase relations among the
various quantities with in the network
• ZR is referred to as the impedance of a resistive element
• Impedance is a measure of how much the element will impede the flow of charge
through the network
• ZR has both magnitude and an associated angle ZR is measured in ohms

4. AC Fundamentals : Power in AC circuits
Ex: Using complex algebra, find the current i for the circuit of Fig.
Sketch the waveforms of v and i.
Waveforms of voltage and current and phasor diagram are shown in Fig

5. AC Fundamentals : Power in AC circuits
Ex: Using complex algebra, find the current v for the circuit of Fig.
Sketch the waveforms of v and i.
Waveforms of voltage and current and phasor diagram are shown in Fig

6. Series-Parallel ac networks: Impedance and Phasor diagram
Inductive Reactance
For a pure inductor, the voltage leads the
current by 90°, and the reactance of the
coil XL is determined by ωL.
Applying Ohm’s law
Since v leads i by 90°, i must have an angle of - 90° associated with it. θL=+90°
Therefore
In time domain
V = 0.707 Vm

7. Series-Parallel ac networks: Impedance and Phasor diagram
Inductive Reactance
In polar form inductive reactance, which is the phase relationship between the
voltage and the current of an inductor is
• ZL is known as the impedance of a inductive element
• ZL has both magnitude and an associated angle
• It is measured in ohms.
• Inductive reactance is a measure of how much the element will control or
impede the level of current through the network.

8. Series-Parallel ac networks: Impedance and Phasor diagram
Ex: Using complex algebra, find the current i for the circuit of Fig.
Sketch the waveforms of v and i

9. Series-Parallel ac networks: Impedance and Phasor diagram
Ex: Using complex algebra, find the current v for the circuit of Fig.
Sketch the waveforms of v and i

10. Series-Parallel ac networks: Impedance and Phasor diagram

11. Series-Parallel ac networks: Impedance and Phasor diagram
Capacitive Reactance
For a pure capacitor of Fig. the current
leads the voltage by 90° and the reactance
of the capacitor XC is determined by 1/ωC.
Applying Ohm’s law
Since i leads v by 90°, i must have an angle of + 90° associated with it. θC=-90°
Therefore
I
n time domain
V = 0.707 Vm

12. Series-Parallel ac networks: Impedance and Phasor diagram
Capacitive Reactance
For a pure capacitor of Fig. the current
leads the voltage by 90° and the reactance
of the capacitor XC is determined by 1/ωC.
Applying Ohm’s law
Since i leads v by 90°, i must have an angle of + 90° associated with it. θC=-90°
Therefore
I
n time domain
V = 0.707 Vm

13. Series-Parallel ac networks: Impedance and Phasor diagram
Capacitive Reactance
In polar form capacitive reactance, which is the phase relationship between
the voltage and the current of a capacitor is
•• ZC is known as the impedance of a capacitive element.
• ZC having both magnitude and an associated angle
• It is measured in ohms.
• Capacitive reactance is a measure of how much the element will control or impede
the level of current through the network.

14. Series-Parallel ac networks: Impedance and Phasor diagram
Capacitive Reactance
In polar form capacitive reactance, which is the phase relationship between
the voltage and the current of a capacitor is
•• ZC is known as the impedance of a capacitive element.
• ZC having both magnitude and an associated angle
• It is measured in ohms.
• Capacitive reactance is a measure of how much the element will control or impede
the level of current through the network.

15. Series-Parallel ac networks: Impedance and Phasor diagram
Ex: Using complex algebra, find the current i for the circuit of Fig.
Sketch the waveforms of v and i

16. Series-Parallel ac networks: Impedance and Phasor diagram
Ex: Using complex algebra, find the current v for the circuit of Fig.
Sketch the waveforms of v and i