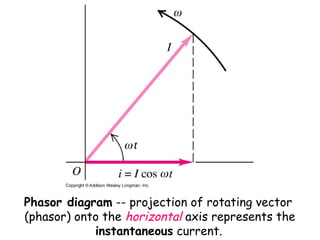
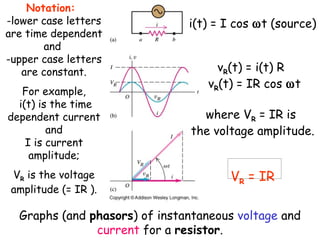
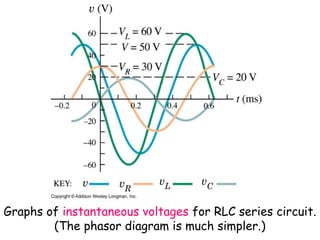
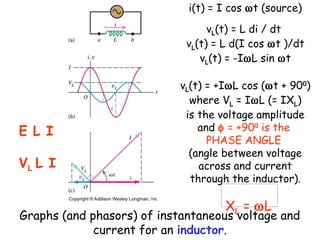
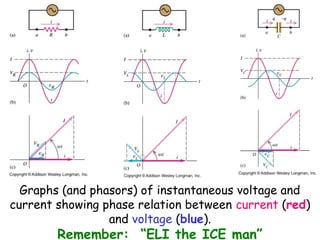
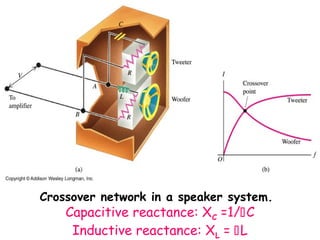
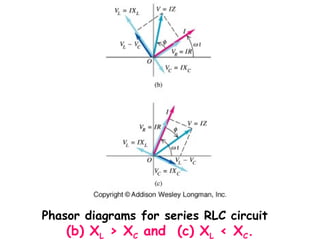
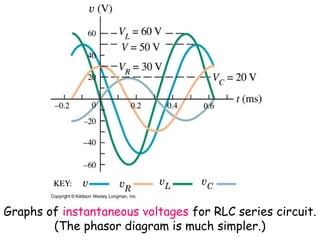
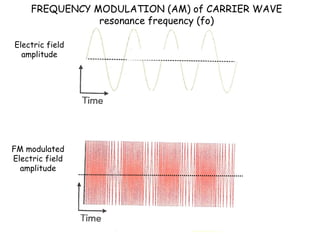
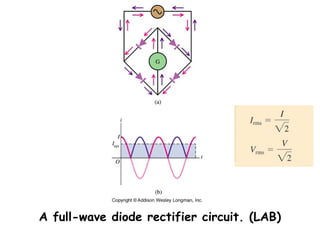
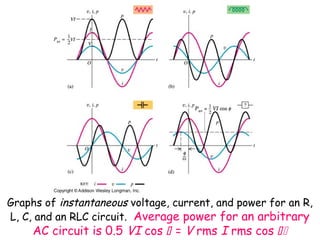
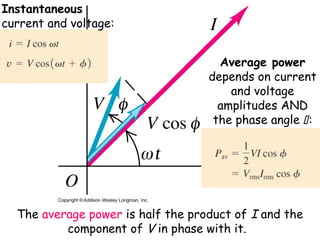
The document provides an overview of key topics in alternating current (AC) circuits covered in Chapter 31, including: 1) The use of phasors to describe sinusoidally varying quantities in AC circuits such as resistors, inductors, and capacitors. 2) Analyzing RLC series circuits driven by a sinusoidal voltage source using phasors. 3) Factors that determine the power in an AC circuit such as the current and voltage amplitudes and their phase relationship. 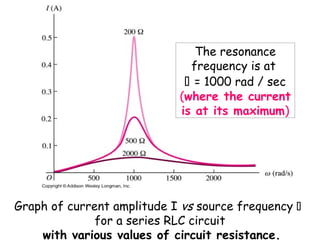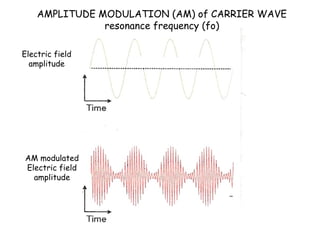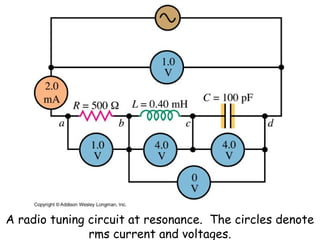4) Resonance in RLC circuits and the effect of frequency on current. 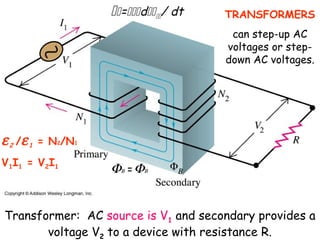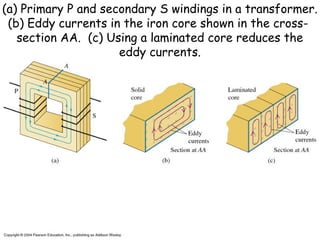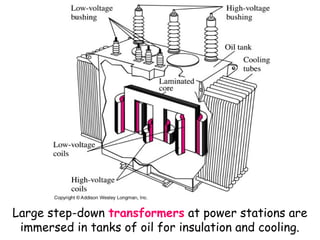5) Transformers and how they can change AC voltages and currents through electromagnetic induction.

1. Alternating Current Ch. 31
Phasors and AC (sec. 31.1)
Resistance and reactance (sec. 31.2) RLC
series circuit (sec. 31.3) Power in
AC circuits (sec. 31.4)
Resonance in AC circuits (sec. 31.5)
Transformers (sec. 31.6)
C 2012 J. F. Becker

2. Learning Goals - we will learn: ch 31
• How phasors make it easy to describe
sinusoidally varying quantities.
• How to analyze RLC series circuits driven
by a sinusoidal emf.
• What determines the amount of power
flowing into or out of an AC circuit.
• How an RLC circuit responds to emfs of
different frequencies.

3. Phasor diagram -- projection of rotating vector
(phasor) onto the horizontal axis represents the
instantaneous current.

4. Notation:
-lower case letters i(t) = I cos ωt (source)
are time dependent
and
-upper case letters
are constant. vR(t) = i(t) R
vR(t) = IR cos ωt
For example,
i(t) is the time
dependent current where VR = IR is
and the voltage amplitude.
I is current
amplitude;
VR is the voltage VR = IR
amplitude (= IR ).
Graphs (and phasors) of instantaneous voltage and
current for a resistor.

5. Graphs of instantaneous voltages for RLC series circuit.
(The phasor diagram is much simpler.)

6. i(t) = I cos ωt (source)
vL(t) = L di / dt
vL(t) = L d(I cos ωt )/dt
vL(t) = -IωL sin ωt
vL(t) = +IωL cos (ωt + 90 ) 0
where VL = IωL (= IXL)
is the voltage amplitude
E L I and φ = +90 is the
0
PHASE ANGLE
(angle between voltage
VL L I across and current
through the inductor).
XL = ωL
Graphs (and phasors) of instantaneous voltage and
current for an inductor.

7. Graphs (and phasors) of instantaneous voltage and
current showing phase relation between current (red)
and voltage (blue).
Remember: “ELI the ICE man”

8. Crossover network in a speaker system.
Capacitive reactance: XC =1/C
Inductive reactance: XL = L

9. Phasor diagrams for series RLC circuit
(b) XL > XC and (c) XL < XC.

10. Graphs of instantaneous voltages for RLC series circuit.
(The phasor diagram is much simpler.)

11. Graphs of instantaneous voltage, current, and power for an R,
L, C, and an RLC circuit. Average power for an arbitrary
AC circuit is 0.5 VI cos  = V rms I rms cos 

12. Instantaneous
current and voltage:
Average power
depends on current
and voltage
amplitudes AND
the phase angle  :
The average power is half the product of I and the
component of V in phase with it.

13. The resonance
frequency is at
 = 1000 rad / sec
(where the current
is at its maximum)
Graph of current amplitude I vs source frequency 
for a series RLC circuit
with various values of circuit resistance.

14. AMPLITUDE MODULATION (AM) of CARRIER WAVE
resonance frequency (fo)
Electric field
amplitude
AM modulated
Electric field
amplitude

15. FREQUENCY MODULATION (AM) of CARRIER WAVE
resonance frequency (fo)
Electric field
amplitude
FM modulated
Electric field
amplitude

16. A radio tuning circuit at resonance. The circles denote
rms current and voltages.

17. =d/ dt TRANSFORMERS
can step-up AC
voltages or step-
down AC voltages.
ε 2 /ε 1 = N2/N1
V1I1 = V2I1
Φ =Φ
Β Β
Transformer: AC source is V1 and secondary provides a
voltage V2 to a device with resistance R.

18. (a) Primary P and secondary S windings in a transformer.
(b) Eddy currents in the iron core shown in the cross-
section AA. (c) Using a laminated core reduces the
eddy currents.

19. Figure 32.2b

20. Large step-down transformers at power stations are
immersed in tanks of oil for insulation and cooling.

21. Figure 31.22

22. Figure 31.23

23. A full-wave diode rectifier circuit. (LAB)

24. A mathematical model of Earth's
magnetic field near the core.
(Courtesy: Gary Glatzmaier)

25. Review
See
www.physics.sjsu.edu/becker/physics51
C 2012 J. F. Becker

26. PREPARATION FOR FINAL EXAM
At a minimum the following should be reviewed:
Gauss's Law - calculation of the magnitude of the electric field caused by
continuous distributions of charge starting with Gauss's Law and completing all the
steps including evaluation of the integrals.
Ampere's Law - calculation of the magnitude of the magnetic field caused by
electric currents using Ampere's Law (all steps including evaluation of the integrals).
Faraday's Law and Lenz's Law - calculation of induced voltage and current,
including the direction of the induced current.
Calculation of integrals to obtain values of electric field, electric potential, and
magnetic field caused by continuous distributions of electric charge and current
configurations (includes the Law of Biot and Savart for magnetic fields).
Maxwell's equations - Maxwell's contribution and significance.
DC circuits - Ohm's Law, Kirchhoff's Rules, series-parallel combinations, power.
Series RLC circuits - phasors, phase angle, current, power factor, average power.
Vectors - as used throughout the entire course.