The document discusses AC motor drives and induction motor drives. It provides details on: 1. AC motor drives are commonly used in industrial and domestic applications due to their light weight, low cost, and low maintenance requirements. Their power control is relatively complex. 2. There are two main types of AC motor drives - induction motor drives and synchronous motor drives. Induction motors are commonly used in adjustable speed drives. 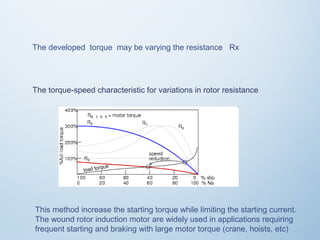3. Speed control of induction motors can be achieved by varying the stator voltage and frequency. Rotor resistance control using an external resistor is also described for wound rotor induction motors.

1. A.C Drives
By
A.S.Krishna

2. AACC DDRRIIVVEESS
AC motor Drives are used in many industrial and
domestic application, such as in conveyer, lift, mixer,
escalator etc.
TThhee AACC mmoottoorr hhaavvee aa nnuummbbeerr ooff aaddvvaannttaaggeess ::
• LLiigghhttwweeiigghhtt ((2200%% ttoo 4400%% lliigghhtteerr tthhaann eeqquuiivvaalleenntt DDCC mmoottoorr))
• IInneexxppeennssiivvee
• LLooww mmaaiinntteennaannccee
TThhee DDiissaaddvvaannttaaggeess AACC mmoottoorr ::
** TThhee ppoowweerr ccoonnttrrooll rreellaattiivveellyy ccoommpplleexx aanndd mmoorree
eexxppeennssiivvee
TThheerree aarree ttwwoo ttyyppee ooff AACC mmoottoorr DDrriivveess ::
11.. IInndduuccttiioonn MMoottoorr DDrriivveess
22.. SSyynncchhrroonnoouuss MMoottoorr DDrriivveess

3. INDUCTION MOTOR DRIVES
Three-phase induction motor are commonly used in adjustable-speed
drives (ASD).
Basic part of three-phase induction motor :
• Stator
• Rotor
• Air gap

4. The stator winding are supplied with balanced three-phase AC voltage,
which produce induced voltage in the rotor windings. It is possible to
arrange the distribution of stator winding so that there is an effect of
multiple poles, producing several cycle of magnetomotive force (mmf) or
field around the air gap.
The speed of rotation of field is called the synchronous speed ws , which
is defined by :
ωs is syncronous speed [rad/sec]
Ns is syncronous speed [rpm]
p is numbers of poles
ω is the supply frequency [rad/sec]
f is the supply frequency [Hz]
Nm p is motor speed
w = 2w
s p
N =120
f s
or

5. The rotor speed or motor speed is : (1 S) m s w =w -
Where S is slip, as defined as :
S = N - N
=w -w Or S
S S m
w
S
S m
N
The motor speed

6. Equivalent Circuit OOff IInndduuccttiioonn MMoottoorr
Where :
Rs is resistance per-phase of stator winding
Rr is resistance per-phase of rotor winding
Xs is leakage reactance per-phase of the
winding stator
Xs is leakage reactance per-phase of the
winding rotor
Xm is magnetizing reactance
Rm is Core losses as a reactance

7. Performance Characteristic of
Induction Motor
Stator copper loss : s cu s s P = 3 I 2 R
3( ' )2 ' r cu r r Rotor copper loss : P = I R
s
P V
c R
m
m
m
V
R
2 2
Core losses : = 3 »3

8. Performance Characteristic of
Induction Motor
- Power developed on air gap (Power from stator to
rotor through air gap) :
P I Rr
g r
S
'
= 3( ' )2
'
P P P I Rr
d g r cu r = - = -
P P (1 S) d g = -
' 2 S
3( ) (1 )
S
- Power developed by motor :
or
- Torque of motor :
T P
d
m
d
w
=
T P
= 60 or
P S
P
g g
w w
s
S
(1 )
S
=
-
-
=
(1 )
or
m
d
d 2p
N

9. Performance Characteristic of
Induction Motor
i s s m P =3V I cosf
c s cu g = P + P + P
Input power of motor :
o d noload P = P - P
Output power of motor :
P -
P
d noload
c s cu g
P
o
i
P P P
P
+ +
h = =
Efficiency :

10. Performance Characteristic of
Induction Motor
( ) g c s cu P >> P + P
If
and
P >> P
d noload so, the efficiency can calculated as :
S
P S
(1 )
d = -
P
P
P
g
g
g
-
» = 1
h

11. Performance Characteristic of
Induction Motor
Generally, value of reactance magnetization X>> value Rm (core
m losses) and also
X 2 >> ( R 2 + X
2 )
m s s So, the magnetizing voltage same with the input voltage : V »V
m s Therefore, the equivalent circuit is ;
Xm

12. Performance Characteristic of
Induction Motor
X X X jX R R
- + + +
=
( ) ( )
'
( )
'
'
'
m s r
R R
r
s
r
m s r m s
i
j X X X
S
S
Z
+ + + +
Total Impedance of this circuit is :
Xm
The rotor current is :
1
ù
( ) 2
' 2
I V
' 2
'
ú ú
û
é
æ
ê ê
ë
ö
+ + ÷ ÷ø
ç çè
R +
R
=
s r
r
s
s
r
X X
S

13. ( )
ù
ú ú
û
T R V
é
æ
S R R
ê ê
ë
3 ' 2
+ + ÷ ÷ø ö
ç çè
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w
Torque – speed Characteristic

14. Three region operation :
1. Motoring :
0£ S £ 1
2. Regenerating :
S < 0
3. Plugging :
1£ S £ 2

15. Performance Characteristic of
Induction Motor
Starting speed of motor is wm = 0 or S = 1,
Starting torque of motor is :
3 ' 2
( )
ù
ú ú
û
T R V
é
æ
ê ê
ë
ö
+ + ÷ ÷ø
ç çè
R +
R
=
' 2
' 2
s r
r
s s
r s
st
X X
S
w
d Td
Slip for the maximum torque Smax can be found by setting : = 0
dS
So, the slip on maximum torque is :
'
S R
r
[( ) 2 ( ' ) 1
2
]2
max
R + X +
X
s s r
= ±

16. Performance Characteristic of
Induction Motor
2
( ) úû ù
T V
êë é
s
R + R + X +
X
=
2 ' 2
max
w
2
3
s s s s r
Torque maximum is :
And the maximum regenerative torque can be found as :
( ) úû ù
T V
êë é
2
s
R R X X
- + + +
=
2 ' 2
max
w
2
3
s s s s r
Where the slip of motor s = - Sm

17. ( )
ù
ú ú
û
T R V
é
S R R
ê ê
ë
3 ' 2
ö
+ + ÷ ÷ø
ç çè æ
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w
Speed-Torque Characteristic :
( X X ' ) 2
R Rr
' ö
2
s r s
÷ ÷ø
æ
ç çè
+ >> +
S
3 ' 2
T R V
r s
( ' )2
d S X +
X
s s r
=
w
3 ' 2
T R V
r s
( ' )2
=
w
st X +
X
s s r
For the high Slip S. (starting)
So, the torque of motor is :
And starting torque (slip S=1) is :

18. For low slip S region, the motor speed near unity or synchronous
speed, in this region the impedance motor is :
X + X ' 2 << R' >>
( ) r
R
s r s
S
3 2
w
T V S
s
d R
'
s r
=
So, the motor torque is :
'
S R
r
[( ) 2 ( ' ) 1
2
]2
max
R + X +
X
s s r
And the slip at maximum torque is : = ±
The maximum motor torque is :
( )
ù
ú úû
T R V
é
æ
S R R
ê êë
3 ' 2
ö
+ + ÷ ÷ø
ç çè
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w

19. Stator Voltage Control
Controlling Induction Motor Speed by
Adjusting The Stator Voltage
( )
ù
ú ú
û
T R V
é
æ
S R R
ê ê
ë
3 ' 2
ö
+ + ÷ ÷ø
ç çè
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w

20. Frequency Voltage Control
Controlling Induction Motor Speed by
Adjusting The Frequency Stator Voltage
( )
ú úû ù
T R V
é
æ
S R R
ê êë
3 ' 2
ö
+ + ÷ ÷ø
ç çè
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w

21. If the frequency is increased above its rated value, the flux and torque
would decrease. If the synchronous speed corresponding to the rated
frequency is call the base speed wb, the synchronous speed at any other
frequency becomes:
s b w =b w
And :
w
m
b
= bw -w =1-
S b m
b
bw
bw
The motor torque :
( )
ù
ú ú
û
T R V
é
æ
S R R
ê ê
ë
3 ' 2
ö
+ + ÷ ÷ø
ç çè
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w
3 ' 2
( )
ù
ú úû
T R V
é
æ
S R R
bw b b
ê êë
ö
+ + ÷ ÷ø
ç çè
+
=
' 2
' 2
s r
r
b s
r s
d
X X
S

22. If Rs is negligible, the maximum torque at the base speed as :
2
T V
( ' )
2
3
s
b s r
mb S X +
X
=
w
And the maximum torque at any other frequency is :
2
3
s
( ) 2
2 '
w b
b s r
m
V
S X X
T
+
=
S R
'
r
s r
At this maximum torque, slip S is : m ( X +
X
' )
=
b
Normalizing :
3
s
( ) 2
2
T V
( ' )
2
3
s
b s r
mb S X +
X
=
w
2
2 '
w b
b s r
m
V
S X X
T
+
=
1
b
2
=
T
m
T
mb
And m mb T b 2 =T

23. Example :
A three-phase , 11.2 kW, 1750 rpm, 460 V, 60 Hz, four pole, Y-connected
induction motor has the following parameters : Rs = 0.1W, Rr’ = 0.38W, Xs =
1.14W, Xr’ = 1.71W, and Xm = 33.2W. If the breakdown torque requiretment is
35 Nm, Calculate : a) the frequency of supply voltage, b) speed of motor at
the maximum torque
Solution :
Input voltage per-phase :
V = 460 =
265
volt s 3
Base frequency : w = 2p f = 2 x 3.14 x 60=377 rad /
s b Nm
x
= 60 = 60 11200
=
p
T =35
Nm m mb 61.11
x x
T P
o
N
m
2 3.14 1750
2
Base Torque :
Motor Torque :
a) the frequency of supply voltage :
1
b
2
=
T
m
T
mb
1.321
= = 61.11 =
35
mb
T
m
b T

24. Synchronous speed at this frequency is :
s b w =b w
x rad s s w =1.321 377 =498.01 / or
rpm
N = N = 60 x 498.01=
4755.65
s b x
2
p
b
p N 4 x
4755.65
So, the supply frequency is : f = = =
Hz s 158.52
b
S
120
120
b) speed of motor at the maximum torque :
S R
'
r
s r
At this maximum torque, slip Sis : m m ( X +
X
' )
=
b
Rr’ = 0.38W, Xs = 1.14W, Xr’ = 1.71W and b = 1.321
0.38 =
( ) 0.101
+
1.3211.14 1.71
= m S
So,
or,
N N S rpm m S = (1- ) = 4755.65(1- 0.101)= 4275

25. CONTROLLING INDUCTION MOTOR SPEED USING
ROTOR RESISTANCE
(Rotor Voltage Control)

26. Wound rotor induction motor applications
cranes

27. CONTROLLING INDUCTION MOTOR SPEED USING
ROTOR RESISTANCE
(Rotor Voltage Control)
Equation of Speed-Torque :
( )
ù
ú úû
T R V
é
æ
S R R
ê êë
3 ' 2
ö
+ + ÷ ÷ø
ç çè
+
=
' 2
' 2
s r
r
s s
r s
d
X X
S
w
3 2
w
T V S
s
d R
'
s r
In a wound rotor induction motor, an external =
three-phase resistor may be connected to its
slip rings,

28. These resistors Rx are used to control motor starting and stopping
anywhere from reduced voltage motors of low horsepower up to
large motor applications such as materials handling, mine hoists,
cranes etc.
The most common applications are:
AC Wound Rotor Induction Motors – where the resistor is wired into the
motor secondary slip rings and provides a soft start as resistance is
removed in steps.
AC Squirrel Cage Motors – where the resistor is used as a ballast for soft
starting also known as reduced voltage starting.
DC Series Wound Motors – where the current limiting resistor is wired to
the field to control motor current, since torque is directly proportional to
current, for starting and stopping.

29. The developed torque may be varying the resistance Rx
The torque-speed characteristic for variations in rotor resistance
This method increase the starting torque while limiting the starting current.
The wound rotor induction motor are widely used in applications requiring
frequent starting and braking with large motor torque (crane, hoists, etc)

30. The three-phase resistor may be replaced by a three-phase diode rectifier and
a DC chopper. The inductor Ld acts as a current source Id and the DC
chopper varies the effective resistance:
R R(1 k) e = -
Where k is duty cycle of DC chopper
The speed can controlled by varying the duty cycle k, (slip power)

31. The slip power in the rotor circuit may be returned to the supply by replacing
the DC converter and resistance R with a three-phase full converter
(inverter)

32. Example:
A three-phase induction motor, 460, 60Hz, six-pole, Y connected, wound rotor
that speed is controlled by slip power such as shown in Figure below. The
motor parameters are Rs=0.041 W, Rr’=0.044 W, Xs=0.29 W, Xr’=0.44 W and
Xm=6.1 W. The turn ratio of the rotor to stator winding is nm=Nr/Ns=0.9. The
inductance Ld is very large and its current Id has negligible ripple.
The value of Rs, Rr’, Xs and Xr’ for equivalent circuit can be considered
negligible compared with the effective impedance of Ld. The no-load of motor is
negligible. The losses of rectifier and Dc chopper are also negligible.
The load torque, which is proportional to speed square is 750 Nm at 1175 rpm.
(a) If the motor has to operate with a minimum speed of 800 rpm, determine
the resistance R, if the desired speed is 1050 rpm,
(b) Calculate the inductor current Id.
(c) The duty cycle k of the DC chopper.
(d)The voltage Vd.
(e)The efficiency.
(f)The power factor of input line of the motor.

33. V = 460 =
265.58
volt s 3
p =6
w =2p x 60=377 rad / s
x rad s s w = 2 377 / 6 =125.66 /
The equivalent circuit :

34. The dc voltage at the rectifier output is :
V I R I R(1 k) d d e d = = -
E = SV N =
r s SV n
s m
r
s
N
and
For a three-phase rectifier, relates Er and Vd as :
V =1.65 x 2 E = 2.3394 E
d r r E = SV N r
Using : =
SV n
r s s m
s
N
d s m V = 2.3394 SV n
P Pr
g =
If Pr is the slip power, air gap power is : S
P P P Pr r
d g r
S P S
= 3( - ) = 3( - ) = 3 (1- )
Developed power is : S
S

35. Because the total slip power is 3Pr = Vd Id and d L m P =T w
So, (1 ) T T (1 S)
P S V I L m L m
d = - = w = w -
S
d d
Substituting Vd from d s m V = 2.3394 SV n In equation Pd above, so
:
Solving for Id gives :
s m
I T
= w
L s
d 2.3394
V n
Which indicates that the inductor current is independent of the speed.
From equation : V I R I R(1 k) d d e d = = - and equation : d s m V = 2.3394 SV n
So, d s m I R(1- k) = 2.3394 SV n
Which gives :
S I R k
= (1- )
s m
d
SV n
2.3394

36. The speed can be found from equation :
S I R k
= (1- ) as :
s m
d
SV n
2.3394
ù
úû
é - = - = -
S I R k
w w (1 ) w 1 (1 )
êë
s m
d
m s s 2.3394
V n
ù
úû
é - = - (2.3394 )2
w w T w R k
1 (1 )
êë
s m
L s
m s V n
Which shows that for a fixed duty cycle, the speed decrease with load
torque. By varying k from 0 to 1, the speed can be varied from minimum
value to ws
rad s m w =180 p / 30 =83.77 /
From torque equation : 2
L v m T = K w
750 800
2
= ÷ø
= æ
ö çè
x 347.67 Nm
1175

37. From equation :
= w The corresponding inductor current is :
s m
I T
L s
d 2.3394
V n
A
I = 347.67 x 125.66 =
78.13
d x x
2.3394 265.58 0.9
The speed is minimum when the duty-cycle k is zero and equation :
ù
úû
êë é - = - = -
S I R k
w w (1 ) w 1 (1 )
s m
d
m s s 2.3394
V n
)
= - R
83.77 125.66(1 78.13
x x
2.3394 265.58 0.9
And : R = 2.3856W