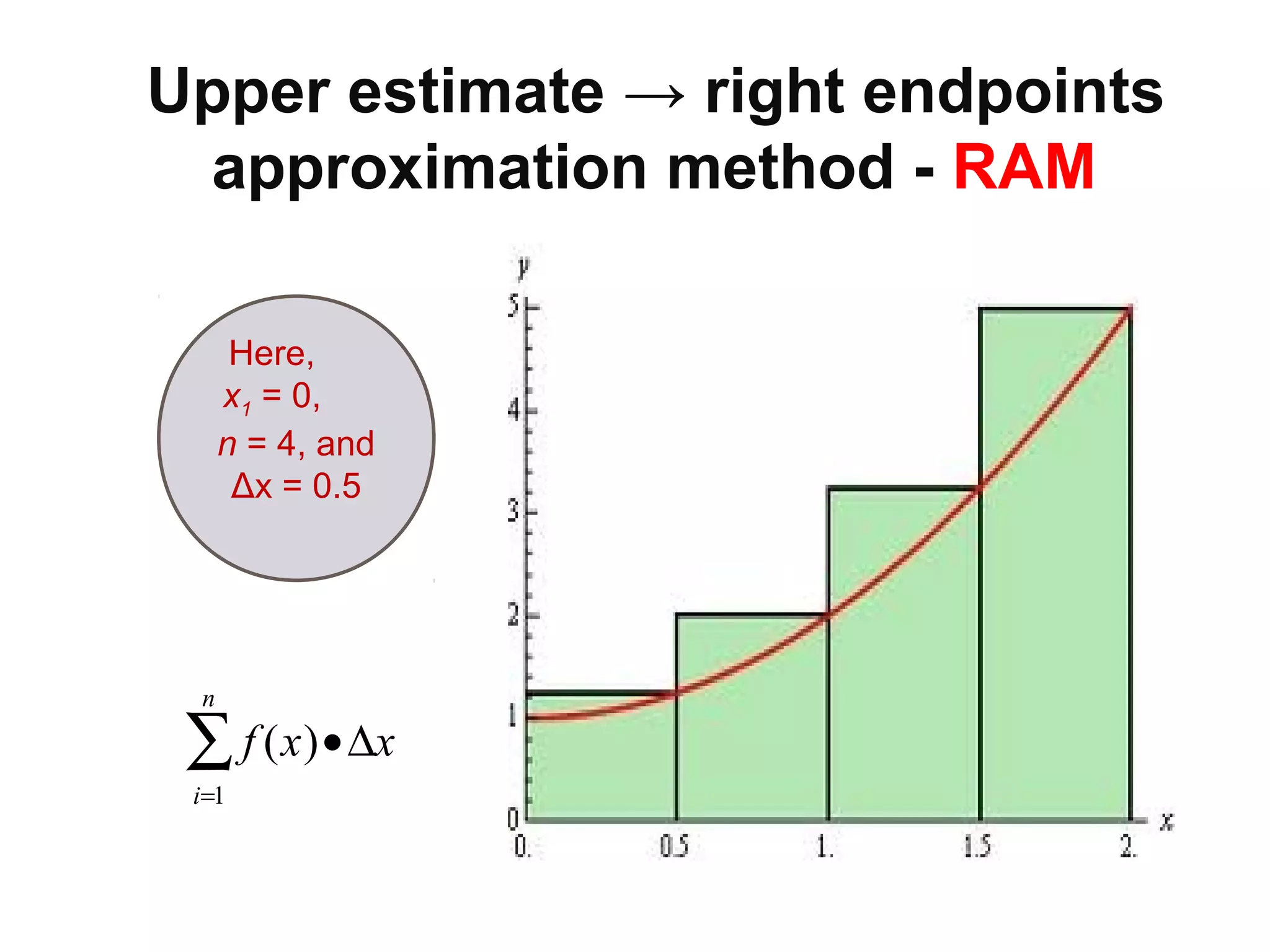
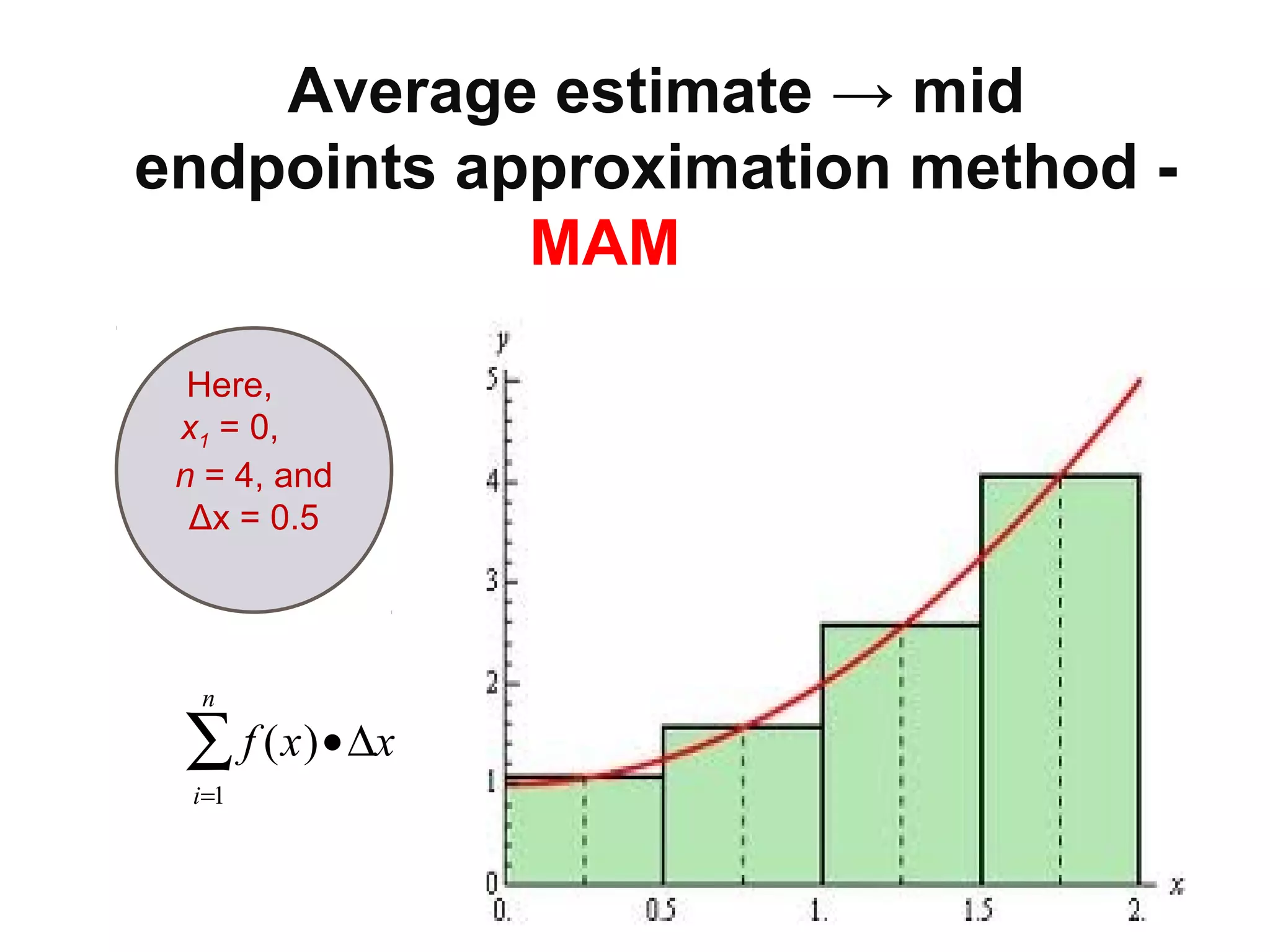
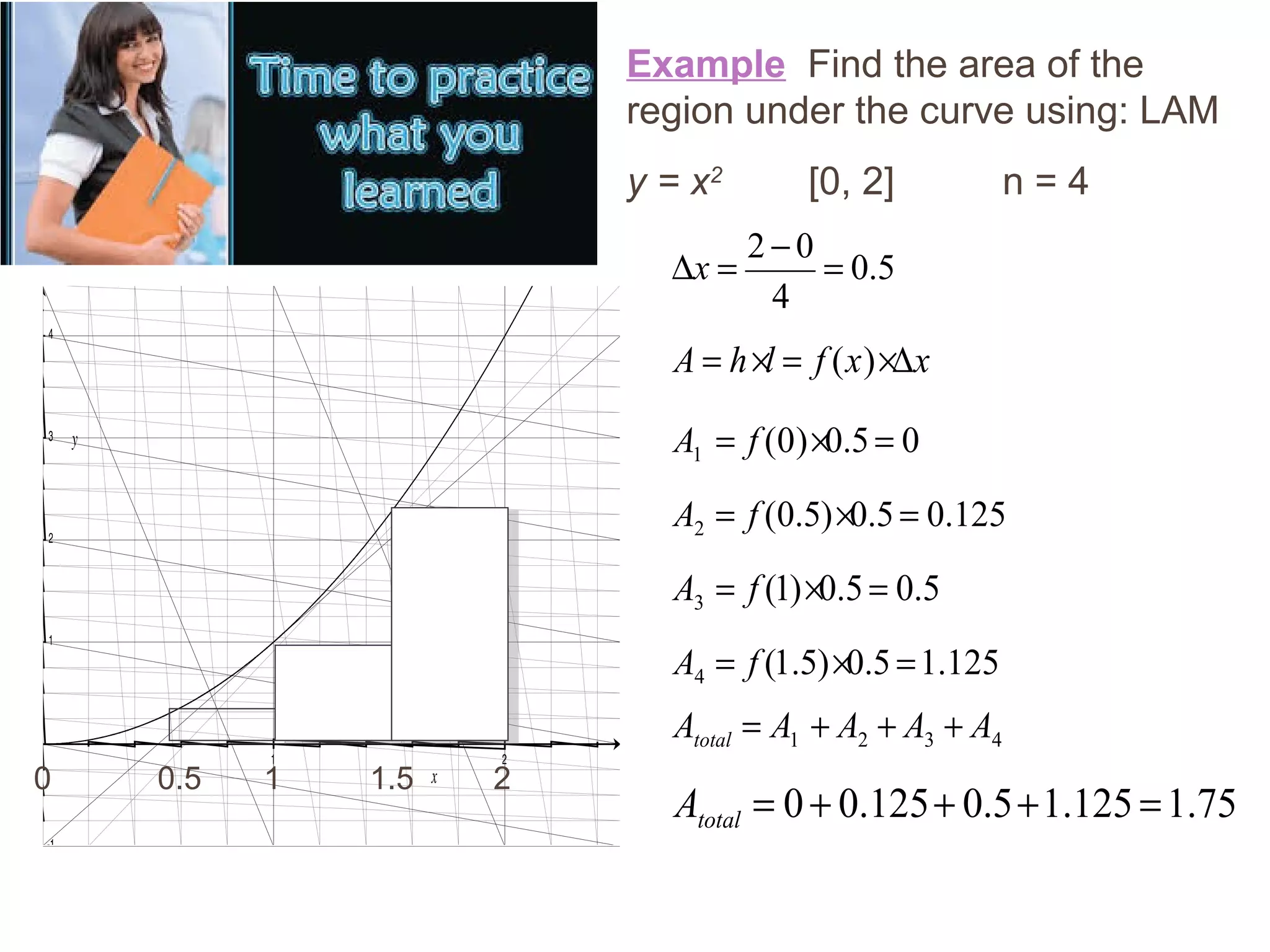
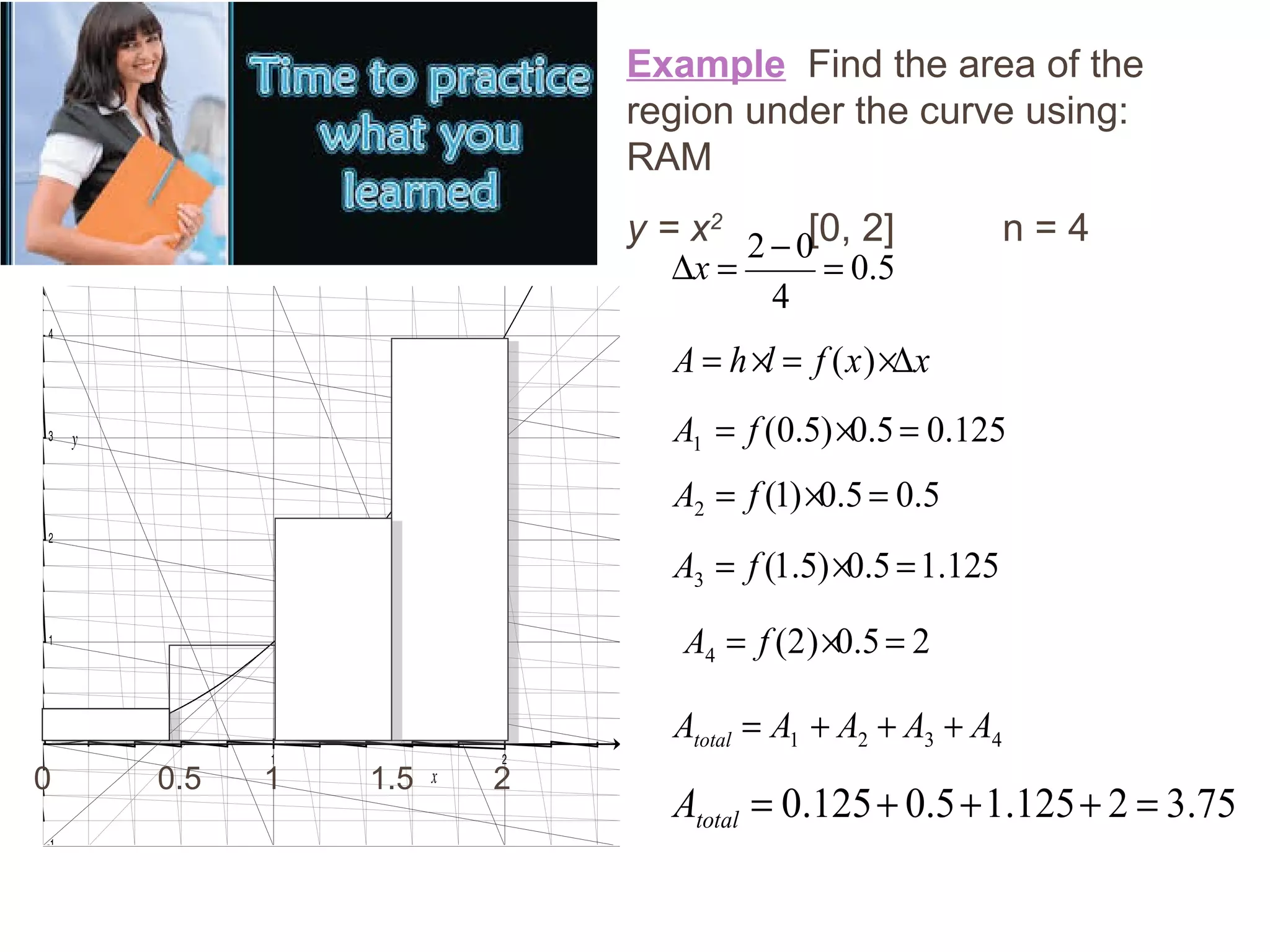
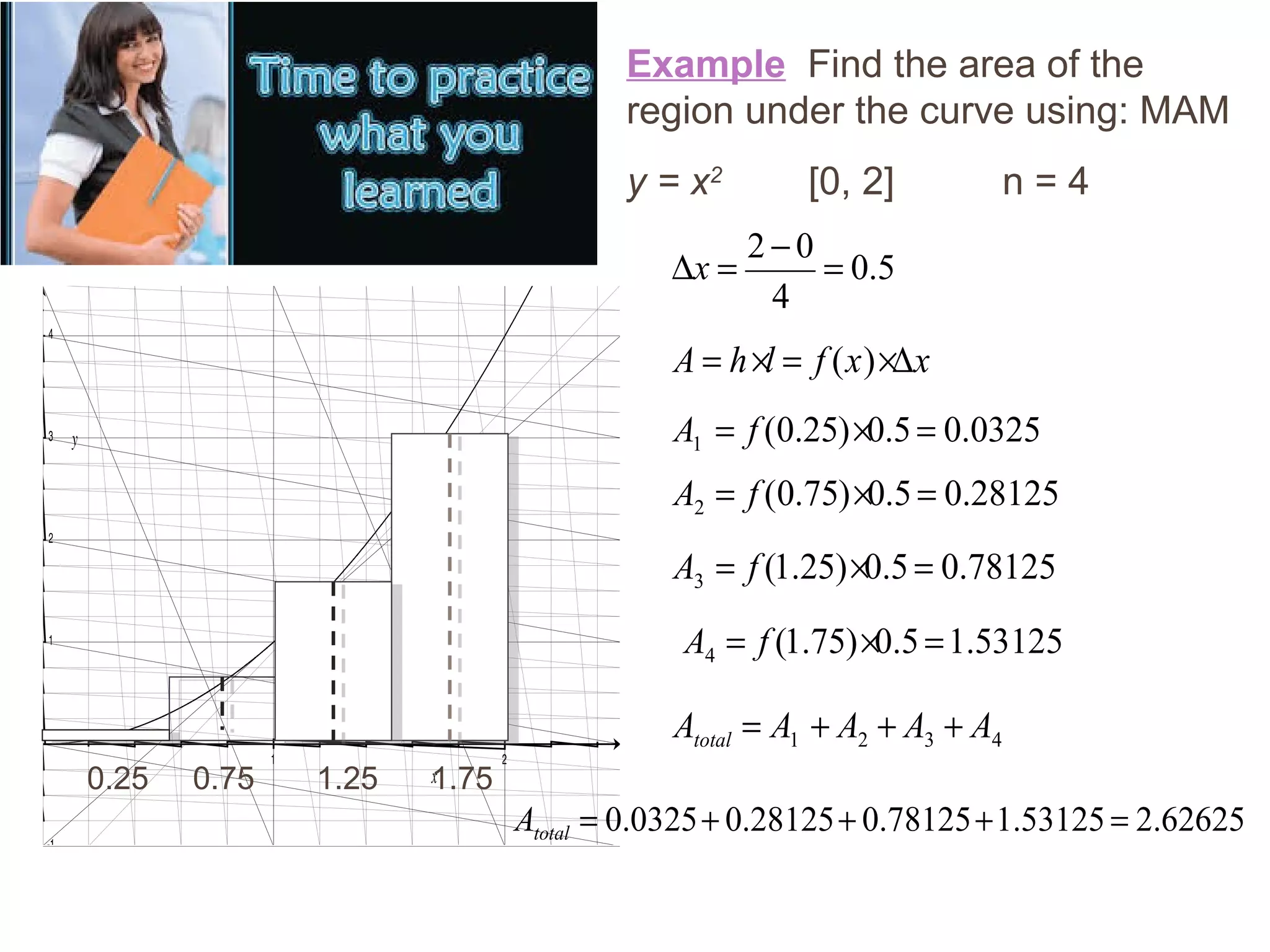
This document discusses two methods for evaluating definite integrals using substitution: 1) ignore the limits of integration and recalculate them at the end, or 2) recalculate the limits of integration at the beginning so they do not need to be revisited later. Examples are provided comparing the two methods on integrals involving trigonometric, exponential, and algebraic substitutions. Practice problems are also included for readers to try the substitution methods.

1. Evaluating Definite Integrals
by Substitution

2. Two Methods for Making
Substitutions in Definite
Integrals
• “Conveniently” ignore the limits of
integration and revisit them at the end
of the process.
• Recalculate the limits in the very
beginning so you don’t have to revisit
them at the end.

3. Let’s see how does that
works without
recalculating limits of
integration.
2
∫ x( x
0
3
2
1/2
I
+1) dx =
∫(x
2
+1)
2
3 I
1
xdx =
2
4 2
∫ u du =
3
 ( x 2 +1)  1  2
1u
 = ( 2 +1) 4 − ( 0 2 +1) 4  =
du = 2xdx
=



 8
2 4
8
0
1
624
= 78
[ 625 −1] =
8
8
u = x 2 +1
4

4. How about
recalculating limits of
integration?
π
8
∫ sin
5
2x cos2xdx =
π
1/2 8
I
0
u = sin 2x
du = 2 cos2xdx
x = 0 → u = sin(0) = 0
π  1
π
x = → u = sin  ÷=
4
8
2
∫ sin 2x
5
0
1
2
1u 

2 6 0
6
2
I
1
cos2xdx =
2
1
2
∫
u5du =
0
 1 6

1
6
= 
÷ − ( 0)  =
12  2 



1 1  1
 − 0 ÷=
12  8  96

5. Practice Time!!!
9
5
1. ∫ ( 2x − 5) ( x − 3) dx =
2
3
4
dx
2. ∫
=
0 1− x
ln3
3. ∫ e x ( 1+ e
0
2
1
x 2
)
dx =
dx
4. ∫ 2
=
1 x − 6x + 9
2
5. ∫ xe
1
− x2
=

6. More!!!
π
6
1. ∫ 2 cos3xdx =
0
(
ln 2
2.
∫
ln 2
3
)
e− x dx
1− e
−2 x
=
2
3. ∫ 5x −1dx =
1
ln 5
4. ∫ e x ( 3 − 4e x ) dx =
0
π
6
5. ∫ tan 2θ dθ =
0

7. More!!!
π
6
1. ∫ 2 cos3xdx =
0
(
ln 2
2.
∫
ln 2
3
)
e− x dx
1− e
−2 x
=
2
3. ∫ 5x −1dx =
1
ln 5
4. ∫ e x ( 3 − 4e x ) dx =
0
π
6
5. ∫ tan 2θ dθ =
0