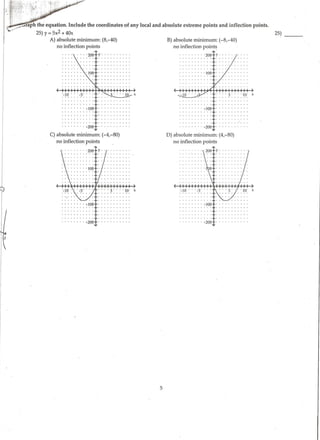
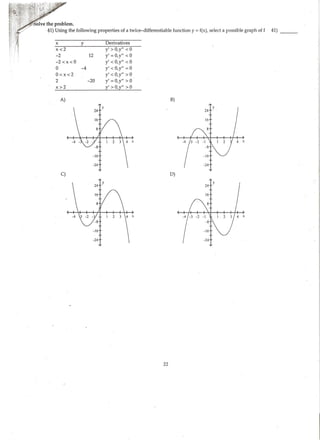
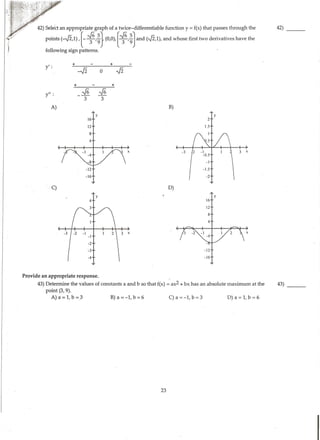
This document contains a practice set of multiple choice questions related to curve sketching and analyzing functions based on their derivatives. There are questions about determining critical points, intervals of increasing/decreasing behavior, locating extrema, and classifying concavity. The document tests skills in analyzing functions through their derivatives to sketch curves and determine properties of the functions.

1. Pr"ctice Set 30 Curve Sketching dlmgutierrez
CtD
Class ID____ Name______________ Date____ Score____
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Using the derivative of f(x) given below, determine the critical points of f(x).
1) f'(x) = (x- 1)2(x + 4) 1) ___
A) -1, 0, 4 B) -4, -1,1 C) -1,4 D) -4,1
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
2) f'(x) = (x- 8)(9- x) 2)
A) Decreasing on (-oo, -8) u (-9, oo); increasing on (-8, -9)
B) Decreasing on (-oo, 8) u (9, oo); increasing on (8, 9)
C) Decreasing on (8, 9); increasing on (-oo, 8) u (9, oo)
D) Decreasing on (-oo, 8); increasing on (9, oo)
3) f'(x) = x1/3(x- 7) 3)
A) Decreasing on (0, 7); increasing on (7, oo)
B) Decreasing on (0, 7); increasing on (-oo, 0) u (7, oo)
C) Increasing on (0, oo)
D) Decreasing on (-oo, 0) u (7, oo); increasing on (0, 7)
Find the open intervals on which the function is increasing and decreasing. Identify the function's local and absolute
extreme values, if any, saying where they occur.
4) 4) - - -
8 y
7
6
4
3
-5 -4 -3 -2 -1
'I
.
2 3 4 5 X
A) increasing on (-2, 0) and (2, 4); decreasing on (0, 2);
absolute maximum at (4, 5) and(0,2); absolute minimum at (-2, 0) and (2, 0)
B) increasing oh (-2, 0) and (2, 4); decreasing on (0, 2);
absolute maximum at (4, 5); absolute minimum at (-2, 0) and (2, 0)
C) increasing on (2, 4); decreasing on (0, 2);
absolute maximum at (4, 5); local maximum at (0, 2); absolute minimum at (-2, 0) and (2, 0)
D) increasing on (-2, 0) and (2, 4); decreasing on (0, 2);
absolute maximum at (4, 5); local maximum at (0, 2); absolute minimum at (-2, 0) and (2, 0)
Find the largest open interval where the function is changing as requested.
5) Increasing y = 7x - 5
A) (-oo, 7) B) (-oo, oo) C) (-5, oo)
1
D) (-5, 7)
5) ---,------

2. 12
1 1
f(x) =-x2 - -x
4 2
A) (-oo, -1)
1
7) Increasing f(x) = - -
x2 + 1
B) (1, oo)
A) (1, oo) B) (-oo, 1)
8) Decreasing f(x) =~
A) (-oo, -4) B) (_:4, oo)
9) Decreasing f(x) =lx - 81
A) (-oo, 8) B) (8, oo)
1
10) Decreasing y =- + 7
x2
A) (-7, 0)
11) Decreasing f(x) =- ~
B) (7, oo)
A)(3,oo) B)(- oo,3)
12) Decreasing f(x) =x3- 4x
A) [-
2
_f1
2
f] B) (-oo, oo)
C) (- oo, oo) D) (-1, 1)
C) (- oo, 0) D) (0, oo)
C) (- oo, 4) D) (4, oo)
C) (- oo, -8) D) (-8, oo)
C)(O, oo) D)(-7,7)
C) (- oo, -3) D) (-3, oo)
D) [-oo, _
2
f]
Identify the function's local and absolute extreme values, if any, saying where they occur.
13) f(x) =-x3- 1.5x2 + 18x - 2
A) local maximum at x = -3; local minimum at x = 2
B) local maximum at x = 2; local minimum at x = -3
C) local maximum at x = -2; local minimum at x =3
D) local maximum at x =3; local minimum at x =-2
14) f(x) =x3+ 9x2 + 27x - 3
A) no local extrema
B) local maximum at x =-3
C) local maximum at x =-3; local minimum at x =3
D) local minimum at x = -3
x4 7
15) g(x) =- - -x3 + 7x2 - 8x- 4
4 3
A) local maxima at x =-1 and x =-4; local minimum at x =2
B) local maximum at x =1; local minimum at x =4
C) local maxima at x =1 and x =4; local minimum at x =2
D) local maximum at x =2; local minima at x =1 and x =4
2
6)
7)
8)
9)
10)
11)
12)
13) - - -
14) - - -
15) - - -

3. / ,11 }1 ~"­•,; :l!·i;i.
·.. " ,tq..~.~·
·:.~~Ht~':·
~:1,1 :<
(!
I.
! '
'
16)_ _
A) no local extrema
B) local min'imum at x = -2; local maximum at x = 6
C) local minimum at x = -5; local maximum at x = 6
D) local minimum at x = -2; no local maxima
17) f(x) = ~x2 + 12x + 72 17) - - -
A) absolute minimum: 6 at x = -6
B) absolute maximum: 6 at x = -6
C) relative minimum: 6 at x = -6; relative maximum: -6 at x = 6
D) no local extrema
Identify the function's extreme values in the given domain, and say where they are assumed. Tell which of the extreme
values, if any, are absolute.
18) f(x) = (x + 7)2, -oo < x :S 0 18)
A) local and absolute maximum: 49 at x = 0;
local and absolute minimum: 0 at x = -7
B) no local extrema; no absolute extrema
C) local and absolute minimum: 0 at x = -7
D) local maximum: 49 at x = 0;
local and absolute absolute minimum: 0 at x = -7
19) h(x) = x3 + 6x2 + 6x + 7, -oo < x s 0
A) local and absolute maximum: 7 at x = 0;
local and absolute minimum: 6 at x = -1
C) !(')cal and absolute maximum: 7 at x = 0;
20) f(x) = ~81- x2, -9 s x < 9
B) no local extrema; no absolute extrema
D) local and absolute minimum: 6 at x = -1;
A) local and absolute minimum: 0 at x = -9 and x = 9;
local and absolute maximum: 9 at x = 0
B) local and absolute minimum: 0 at x = -9;
local and absolute maximum: 9 at x = 0
C) no local extrema; no absolute extrema
D) local and absolute maximum: 0 at x = -9;
local and absolute minimum: 9 at x = 0
Find the extrema of the function on the given interval, and say where they occur.
21) sin 4x, 0 s x s~
. 2
A) local maxima: 1 at x = ~ and 0 at x = ; ;
local minima: 0 at x = 0 and -1 at x =
371
8 •
C) local maxima: 1 at x =~and 0 at x = ~;
8 2
I I . ~ 1 371
oca m1mmum: - at x = S
B) local maxima: 1 at x =~ and 0 at x = ~;
8 . 2
local minima: 0 at x = 0 and -1 at x =
3
8
71
D) local maxima: 1 at x = ~ and 0 at x = ~;
8 4
local minimum: 0 at x = 0
3
19) _ _
20)
21) - - -

4. 22) sin x +cos x, 0 ~ x ~ 2n
A) local maxima: 1 at x =0 and -,J2 at x = 7
4
n;
local minima: 1 at x =2n and ,fiat x = ~
B) local maxima: 1 at x =2n and ,fiat x = ~;
local minima: 1 at x = 0 and -,J2 at x =
5
4
n
C) local maxima: 1.at x =0 and -,J2 at x = 5
4
n;
local minima: 1 at x =2n ~nd ,fiat x = ~
D) local maxima: 1 at x =2n and ,fiat x = ~;
local minima: 1 at x = 0 and -,J2 at x = 7
4
n
23) csc2x + 2 cot x, 0 < x < n
A) local maximum: 0 at x = 3
4
n
C) local maximum: 0 at x = ~
B) local minimum: 0 at x = ~
D) local minimum: 0 at x = 3
4
n
22)
23)
Use the graph ofthe function f(x) to locate the local extrema and identify the intervals where the function is concave up
and concave down.
24)
- 10 -5 10 X
-5
-10
A) Local minimum at x =1; local maximum at x =-1; concave up on (- oo, oo)
B) Local minimum at x =1; local maximum at x =-1; concave down on (- oo, oo)
C) Local minimum at x =1; local maximum at x =-1; concave up on (0, oo); concave down on
(-oo, 0)
D) Local minimum at x = 1; local maximum at x =-1; concave down on (0, oo); concave up on
(-oo, 0)
4
24) - - -

5. J)
.t .
? raph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
. 25) y = sx2 + 40x 25) - - -
A) absolute minimum: (8,-40) B) absolute minimum: (-8,-40)
rio inflection points no inflection points
· · · · · · · · ·wo Y· · · · · · · · · ·
·-w···s···
........ ' 1'()0
· · · · · · · · ,wo · · · · · · · · · · ·
C) absolute minimum: (-4,- 80)
no inflection points
.. .. .. .. ·wo y ...... • .. ·
· · · · s· · · · ro· x
. . ...... '1'00
...... ; ....
· · · · · · · · ,wo
5
· · · · · · · · ·wo Y· · · · · · · · · ·
...... 1'00
· · · · s · · · · ro· x
........ , 1'()0
· · · · · · · · ,wo · · · · · · · ·
D) absolute minimum: (4,-80)
no inflection points
y .... .. ....
'- 10 .. '-'5' ...
. . . . . . . . . . .
. . . . . . . . , 1'00
· · · · · · · · ,wo

6. 41)
X y Derivatives
x<2 y' > O,y" < 0
-2 12 y' = O,y" < 0
I
-2 <X< 0 y' < O,y" < 0
0 -4 y' < O,y" = 0
0<x<2 y' < O,y" > 0
2 -20 y' = O,y" > 0
x>2 y' > O,y" > 0
A) B)
C) D)
22

7. + +
--J2 0 -J2
y':
+ +
_-16 -J6
3 3
y":
A) B)
y y
16 2
12 1.5
8
4
-3 3 X
C) D)
y
16
12
8
4
3 X -I X
-4
-2
-3 -12
-4 -16
Provide an appropriate response. .
43) Determine the values of constants a and b so that f(x) =ax2 + bx has an absolute maximum at the 43)
---point (3, 9).
A) a =1, b =3 B) a =-1, b =6 C) a =-1, b =3 D) a =1, b =6
23
I