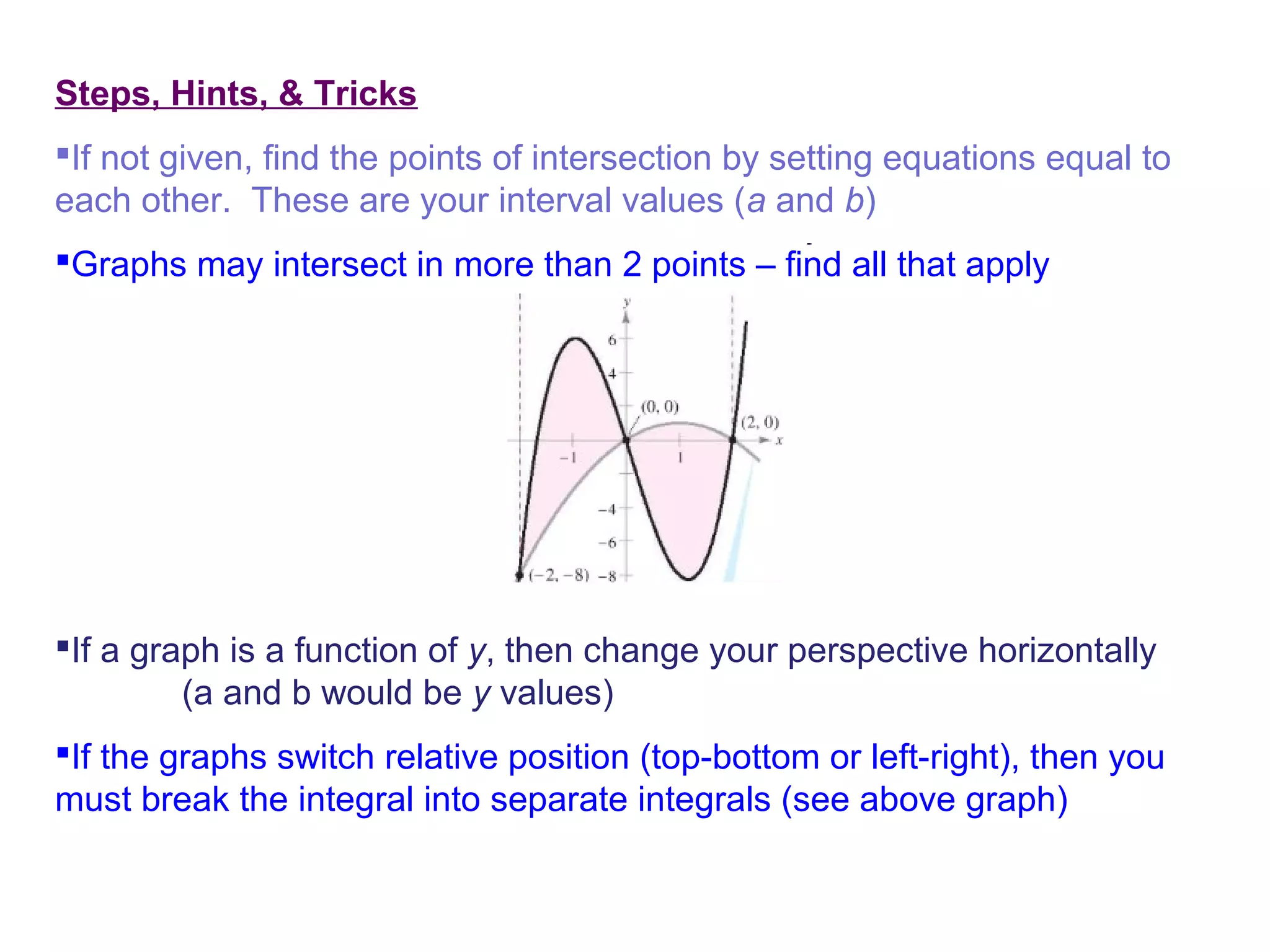
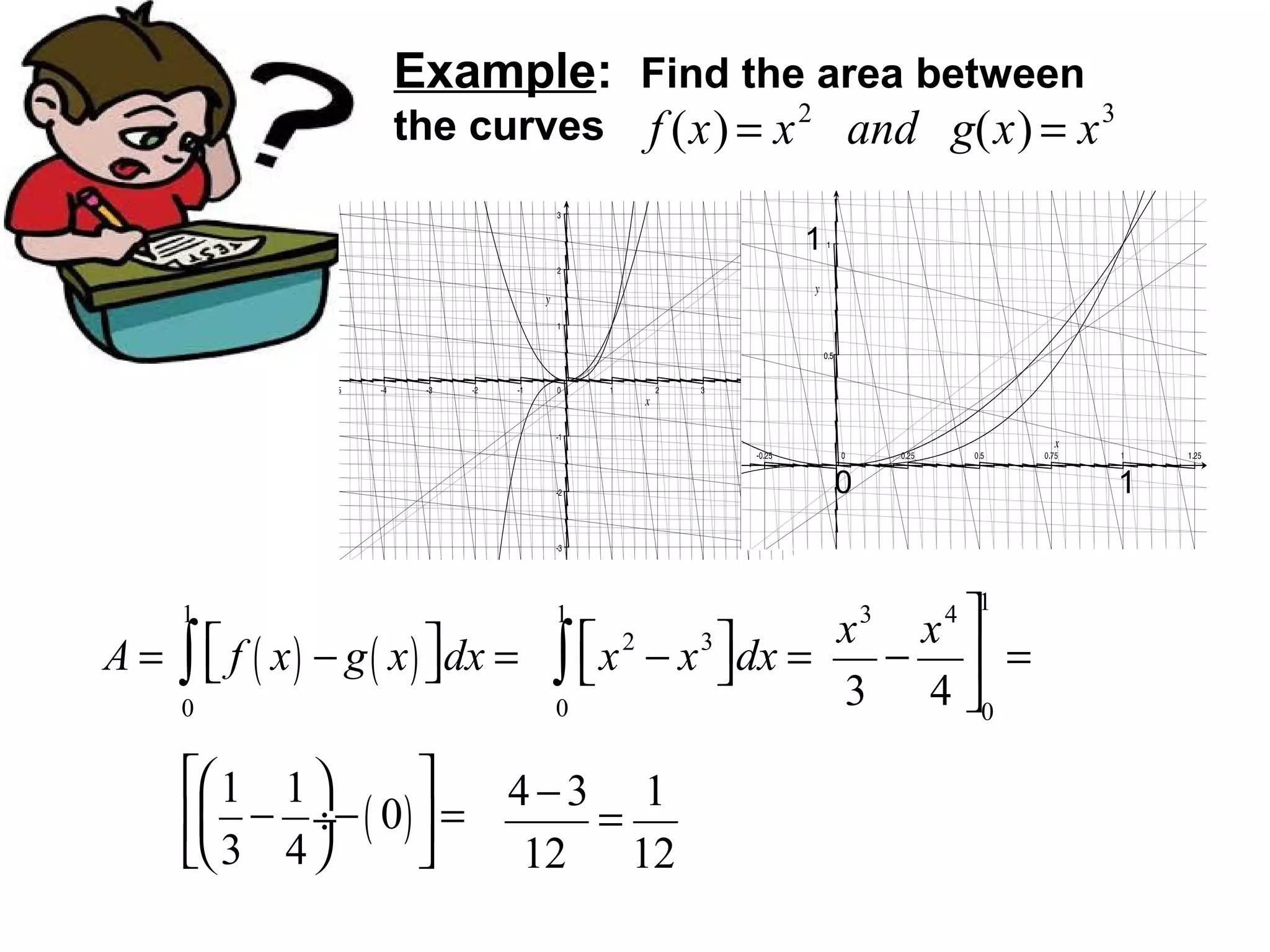
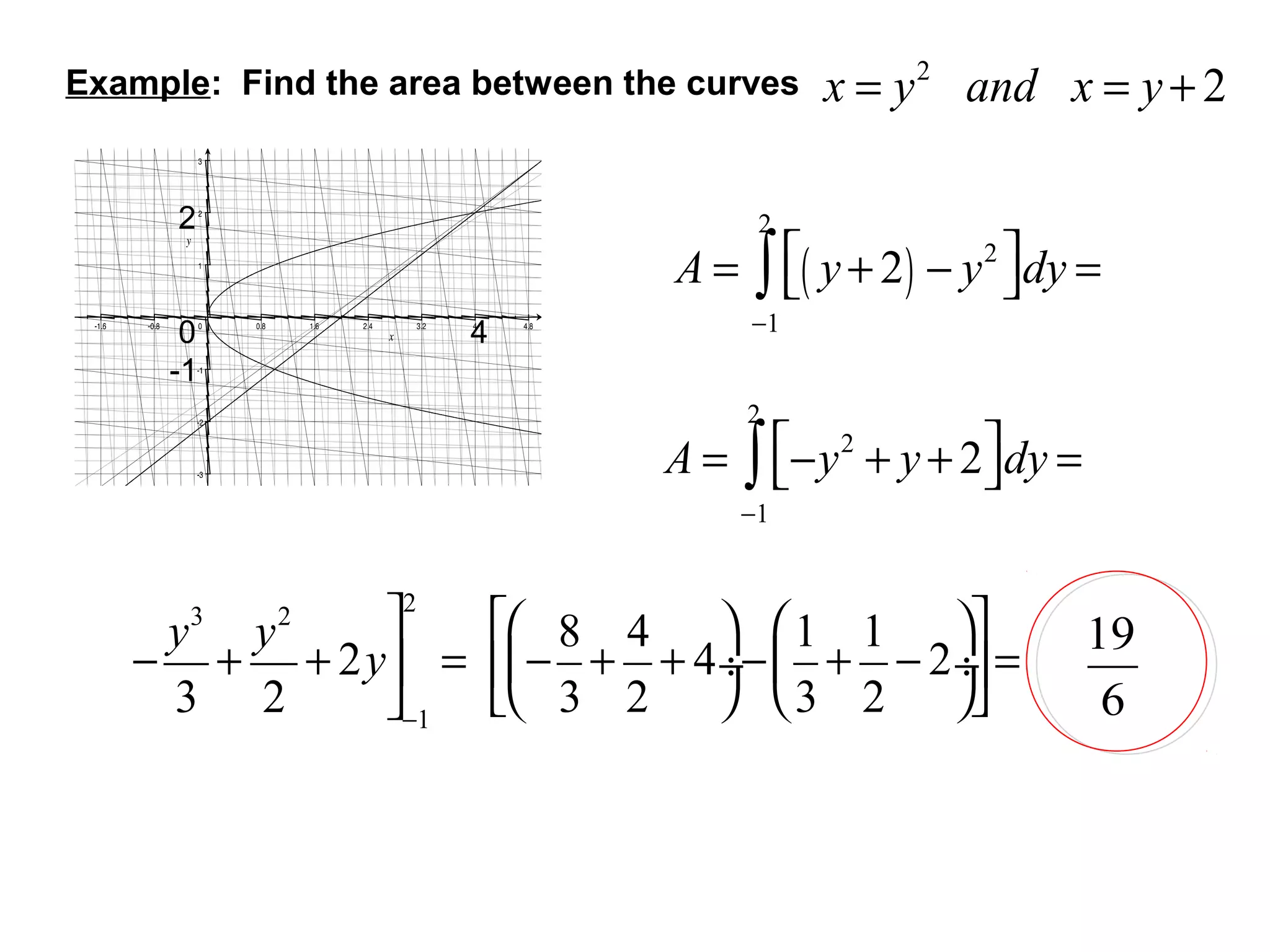
The document discusses calculating the area between two curves. It explains that this area is defined as the limit of the sum of the areas of rectangles between the curves as the number of rectangles approaches infinity, which is represented by a definite integral. It provides examples of finding the area between curves defined by various functions through setting up and evaluating the appropriate definite integral.

1. Area Between
Curves

2. The Big Picture
=
-

3. “Proof”
Find the limit of the area of rectangles given by a
representative rectangle:
The area would be the limit of
the sum of the areas of infinite
representative rectangles with
infinitely small intervals (n → ∞):
n
lim ∑ [ f ( xi ) − g ( xi ) ] ∆x
n →∞
i −1
This is the integral:
b
∫ [ f ( x ) − g ( x ) ] dx
a

4. Steps, Hints, & Tricks
If not given, find the points of intersection by setting equations equal to
each other. These are your interval values (a and b)
Graphs may intersect in more than 2 points – find all that apply
If a graph is a function of y, then change your perspective horizontally
(a and b would be y values)
If the graphs switch relative position (top-bottom or left-right), then you
must break the integral into separate integrals (see above graph)

5. Example: Find the area between
the curves f (x) = x 2 and g(x) = x 3
1
0
1
4 1
x x 
−  =
A = ∫  f ( x ) − g ( x )  dx = ∫  x − x  dx =




3 4 0
0
0
1
1
2
 1 1 

4−3 1
− ÷− ( 0)  =
=

 3 4 

12 12
3
3

6. Example: Find the area between the curves y1 =
3
0
1
−1
x and y2 = x
0
A = ∫  x − 3 x  dx + ∫  3 x − x dx =




4 0
3
1


2
x 3x  3x
x 
−
 + 4 − 2 =
2
4
−1
0


2
4
3
  1 3   3 1 
= 0 −  − ÷ +  − − 0 =
  2 4   4 2 
−4 + 6 + 6 − 4 4 1
= =
8
8 2

7. Area Between Curves
A=
x2
( top − bottom ) dx
∫
x1
A=
y2
( right − left ) dy
∫
y1

8. Example: Find the area between the curves
2
x = y 2 and x = y + 2
2
A = ∫ ( y + 2 ) − y 2  dy =


0
-1
4
−1
2
A = ∫ −y 2 + y + 2 dy =


−1
2

y y
− + + 2y =
3 2
−1
3
2
 8 4   1 1 
 − + + 4 ÷−  + − 2 ÷ =
 3 2   3 2 
19
6