Recommended
PPTX
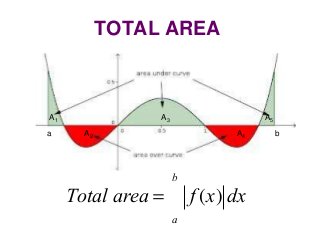
6.5 & 6.6 & 6.9 the definite integral and the fundemental theorem of calculus...
PDF
PDF
موقع ملزمتي - مراجعة ليلة الامتحان هندسة للصف الأول الثانوي
PDF
PDF
موقع ملزمتي - ملزمة هندسة للصف الثالث الإعدادي الترم الثاني
PPTX
DOCX
matematika kalkulus indonesia
PDF
DOCX
PPTX
PDF
Exercícios de Trigonometria Resolvidos
PDF
Kalkulus modul 3a turunan fungsi revisi
PDF
PDF
Ejercicios de antiderivadas
DOCX
Дээд математик 3 MT103 бодлого
PDF
CM 1.0 geometry2 MrG 20110913 - sage
PDF
Persamaan Parabola, Elips dan Hiperbola
PDF
Chu de hinh hoc giai tich trong mat phang
PDF
PDF
DOCX
PDF
DOCX
PPT
8.7 numerical integration
PPTX
PPTX
7.3 volumes by cylindrical shells
PPTX
7.2 volumes by slicing disks and washers
PPT
PPTX
6.5 & 6.6 & 6.9 the definite integral and the fundemental theorem of calculus...
PPT
6.3 integration by substitution
More Related Content
PPTX
6.5 & 6.6 & 6.9 the definite integral and the fundemental theorem of calculus...
PDF
PDF
موقع ملزمتي - مراجعة ليلة الامتحان هندسة للصف الأول الثانوي
PDF
PDF
موقع ملزمتي - ملزمة هندسة للصف الثالث الإعدادي الترم الثاني
PPTX
DOCX
matematika kalkulus indonesia
PDF
What's hot
DOCX
PPTX
PDF
Exercícios de Trigonometria Resolvidos
PDF
Kalkulus modul 3a turunan fungsi revisi
PDF
PDF
Ejercicios de antiderivadas
DOCX
Дээд математик 3 MT103 бодлого
PDF
CM 1.0 geometry2 MrG 20110913 - sage
PDF
Persamaan Parabola, Elips dan Hiperbola
PDF
Chu de hinh hoc giai tich trong mat phang
PDF
PDF
DOCX
PDF
DOCX
More from dicosmo178
PPT
8.7 numerical integration
PPTX
PPTX
7.3 volumes by cylindrical shells
PPTX
7.2 volumes by slicing disks and washers
PPT
PPTX
6.5 & 6.6 & 6.9 the definite integral and the fundemental theorem of calculus...
PPT
6.3 integration by substitution
PPT
6.2 the indefinite integral
PPT
6.1 & 6.4 an overview of the area problem area
PPTX
PPT
5.7 rolle's thrm & mv theorem
PPTX
PPTX
5.4 absolute maxima and minima
PPTX
PPT
5.2 first and second derivative test
PPT
5.1 analysis of function i
PPT
4.3 derivatives of inv erse trig. functions
PPTX
7.2 volumes by slicing disks and washers
PPTX
PPT
8.7 numerical integration
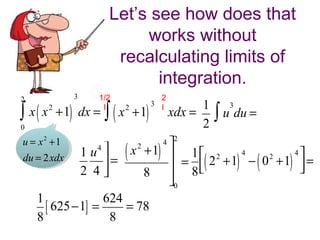
6.3 integration by substitution 1. 2. This method used the sum of
the area of intervals under a
curve- called Reimann Sums
3. The limit of the sums of intervals is the same as
a definite integral over the same interval.
6. • A’ (x) = f (x)
• A (a) = 0
and F (x) = A (x) + C
• A (b) = A
A (x)
b
F ( b ) - F ( a ) = é A ( b) + C ù - é A ( a ) + C ù =
ë
û ë
û
A ( b) - A ( a ) =
A-0 =
A
7. 8. How about some
practice?
ù
3
3
3
3
2x ú
2 æ 2 2 ö 2 æ 9 2 -12 ö = 2 27 -1 = 52
x dx = ò x dx =
÷
(
)
= ç 9 -1 ÷ = ç
ú
3è
3
ø 3
3è
3
1
ø
ú1
û
9
1. ò
9
1
p
3 9
2
1
2
p
ù
cos x ù 2
sin x
1é æp ö
= - êcos ç ÷ - cos0ú = - 1 [ 0 -1] = 1
2. ò
dx = ú
5 û0
5
5ë è 2 ø
û
5
5
0
2
ù = 5 ( eln3 - e0 ) = 5 (3-1) =10
3. ò 5e dx = 5e û0
ln3
0
x
x ln3
9. More Examples !!!
6
Evaluate
ò f (x)dx If
0
2
ò
0
ì x 2,
ï
f (x) = í
ï3x - 2,
î
x<2
x³2
ù
x ù 3x 2
2
x dx + ò (3x - 2) dx =
- 2x ú =
ú +
3 û0 2
û2
2
6
æ8 ö
128
ç - 0 ÷ + ( 42 - 2) =
è3 ø
3
3 2
6
10.





![The Fundamental Theorem
of Calculus, Part I
b
ò
a
f ( x ) dx = F(x)] a
b](https://image.slidesharecdn.com/6-131206202557-phpapp01/85/6-3-integration-by-substitution-7-320.jpg)
![How about some
practice?
ù
3
3
3
3
2x ú
2 æ 2 2 ö 2 æ 9 2 -12 ö = 2 27 -1 = 52
x dx = ò x dx =
÷
(
)
= ç 9 -1 ÷ = ç
ú
3è
3
ø 3
3è
3
1
ø
ú1
û
9
1. ò
9
1
p
3 9
2
1
2
p
ù
cos x ù 2
sin x
1é æp ö
= - êcos ç ÷ - cos0ú = - 1 [ 0 -1] = 1
2. ò
dx = ú
5 û0
5
5ë è 2 ø
û
5
5
0
2
ù = 5 ( eln3 - e0 ) = 5 (3-1) =10
3. ò 5e dx = 5e û0
ln3
0
x
x ln3](https://image.slidesharecdn.com/6-131206202557-phpapp01/85/6-3-integration-by-substitution-8-320.jpg)