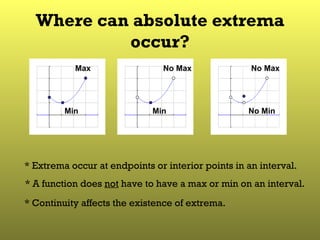
1) A function has an absolute maximum value on its domain if its value is greater than or equal to its value at all other points in its domain, and an absolute minimum value if its value is less than or equal to its value at all other points. 2) By the Extreme Value Theorem, if a function is continuous on a closed interval, it will have both an absolute maximum and minimum value within that interval. These extreme values can occur at interior points or endpoints. 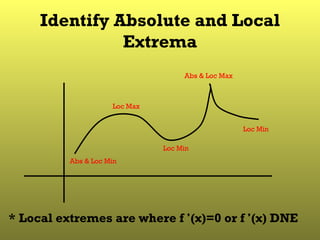3) A local extreme value of a function is a maximum or minimum value within a neighborhood of some interior point, where the function's derivative is equal to 0 or undefined at that point, according to the Local Extreme Value Theorem.

1. 4.1 Extreme Values of Functions

2. Def : Absolute Extreme Values Let f be a function with domain D. Then f (c) is the… a) Absolute (or global) maximum value on D iff f (x) ≤ f (c) for all x in D. b) Absolute (or global) minimum value on D iff f (x) ≥ f (c) for all x in D. * Note: The max or min VALUE refers to the y value.

3. Where can absolute extrema occur? * Extrema occur at endpoints or interior points in an interval. * A function does not have to have a max or min on an interval. * Continuity affects the existence of extrema. Min Max Min No Max No Max No Min

4. Thm 1 : Extreme Value Theorem If f is continuous on a closed interval [a,b], then f has both a maximum value and a minimum value on the interval. * What is the “worst case scenario,” and what happens then?

5. Def : Local Extreme Values Let c be an interior point of the domain of f . Then f (c) is a… a) Local (or relative) maximum value at c iff f (x) ≤ f (c) for all x in some open interval containing c. b) Local (or relative) minimum value at c iff f (x) ≥ f (c) for all x in some open interval containing c. * A local extreme value is a max or min in a “neighborhood” of points surrounding c

6. Identify Absolute and Local Extrema * Local extremes are where f ’ (x)=0 or f ’ (x) DNE Abs & Loc Min Abs & Loc Max Loc Max Loc Min Loc Min

7. Thm 2 : Local Extreme Values If a function f has a local maximum value or a local minimum value at an interior point c of its domain, and if f ’ exists at c , then f ’(c)=0.

8. Def : Critical Point A critical point is a point in the interior of the domain of f at which either… 1) f ’(x)= 0 , or 2) f ’(x) does not exist

9. Finding Absolute Extrema on [a,b]… To find the absolute extrema of a continuous function f on [a,b]… Evaluate f at the endpoints a and b. Find the critical numbers of f on [a,b]. Evaluate f at each critical number. Compare values. The greatest is the absolute max and the least is the absolute min.

10. Check for Understanding… (True or False??) Absolute extrema can occur at either interior points or endpoints. A function may fail to have a max or min value. A continuous function on a closed interval must have an absolute max or min. An absolute extremum is also a local extremum. Not every critical point or end point signals the presence of an extreme value.