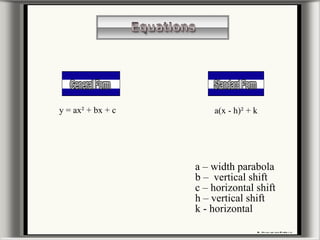
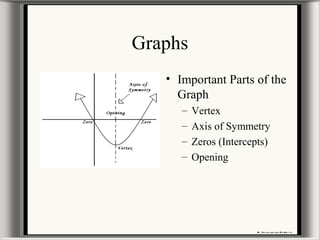
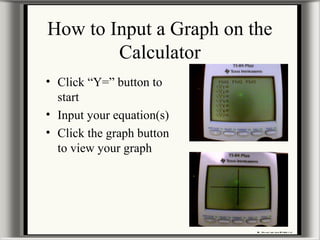
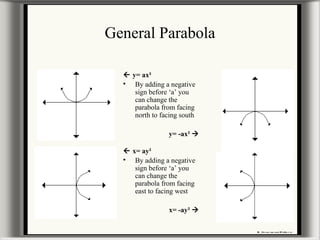
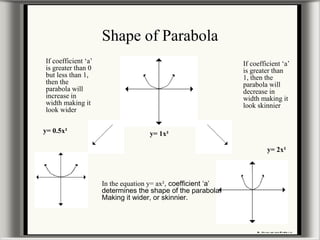
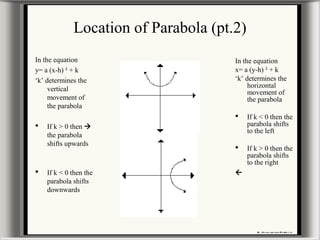
This document provides information about graphing parabolas on a graphing calculator. It discusses the key parts of a parabola graph like the vertex, axis of symmetry, zeros, and y-intercept. It explains how to input equations into the graphing calculator and use functions to find the vertex, zeros, and maximum or minimum points. The document also covers how changing variables in the standard parabola equation affects the shape, direction, and location of the graphed parabola. Some examples of word problems involving parabolas are presented as well.

1. Roxee
Joseph
Paulo
Thang

2. a(x - h)² + ky = ax² + bx + c
a – width parabola
b – vertical shift
c – horizontal shift
h – vertical shift
k - horizontal

3. Graphs
• Important Parts of the
Graph
– Vertex
– Axis of Symmetry
– Zeros (Intercepts)
– Opening

4. Important Parts of the Graph
• Vertex
– The Min/Max point of
the Parabola
• Axis of Symmetry
– Imaginary line that
goes through the
vertex. It splits the
parabola into two
mirror images
• Zeros
– Point(s) on the graph
where it crosses the X-
axis
• Y-intercept
– Point on the graph
were it crosses the Y-
axis
• Opening

5. How to Use a Graphing
Calculator
• Buttons to know:
– Y=
– Graph
– Trace
– Window
– Variable

6. What do the Buttons do?
• Y=
– Area where you input
equation(s) of the
graph
• Graph
– Shows the graph(s)
• Window
– Adjusts the graph’s
min/max X and Y
values
• Trace
– Able to run along the
graph
– Second Function
(calculate): Is able to
find the min/max
value, zeros, etc. of
graph
• Variable
– Easy access to
variables

7. How to Input a Graph on the
Calculator
• Click “Y=” button to
start
• Input your equation(s)
• Click the graph button
to view your graph

8. How to find the Vertex of your
Graph
• 2nd
Function > Trace
• Select Min or Max
depending on the
opening of the graph
• Select a point on the
left side of the vertex
then the right side of it,
then take a guess at
what it could be
• Vertex will show up at
the bottom of screen

9. How to find the Zero’s of the
Graph
• 2nd
Function > Trace
• Select Zero’s
• Choose a point on the left side of a zero then a
right (points must have different signs), lastly
take a guess
• Zero will show up at the bottom of screen
• Usually needed to be done twice

10. Transformations
“By changing the equation, you can change the
shape, the direction it is pointing, and the location
of the parabola”

11. General Parabola
 y= ax²

By adding a negative
sign before ‘a’ you
can change the
parabola from facing
north to facing south
y= -ax² 
 x= ay²

By adding a negative
sign before ‘a’ you
can change the
parabola from facing
east to facing west
x= -ay² 

12. Shape of Parabola
y= 1x²y= 0.5x²
y= 2x²
In the equation y= ax², coefficient ‘a’
determines the shape of the parabola.
Making it wider, or skinnier.
If coefficient ‘a’
is greater than 0
but less than 1,
then the
parabola will
increase in
width making it
look wider
If coefficient ‘a’
is greater than
1, then the
parabola will
decrease in
width making it
look skinnier

13. Location of Parabola
In the equation
y= a (x-h) ²
‘h’ determines the
horizontal
movement of
the parabola
 If h > 0 then 
the parabola
shifts to the
right
 If h < 0 then the
parabola shifts
to the
left
In the equation
x= a (y-h) ²
‘h’ determines the
vertical
movement of
the parabola
 If h < 0 then the
parabola shifts
to the
upwards
 If h > 0 then the
parabola shifts
downwards

y= a (x-2) ²
x= a (y-2) ²

14. Location of Parabola (pt.2)
In the equation
y= a (x-h) ² + k
‘k’ determines the
vertical
movement of
the parabola
 If k > 0 then 
the parabola
shifts upwards
 If k < 0 then the
parabola shifts
downwards
In the equation
x= a (y-h) ² + k
‘k’ determines the
horizontal
movement of
the parabola
 If k < 0 then the
parabola shifts
to the left
 If k > 0 then the
parabola shifts
to the right


15. Completing a Square
y= ax²+bx+c
Example One Example Two Example Three
y= x² +6x-7 y= 3x² +24x+21 y= 2x² +5x+2
= (x² +6x+_9_)-7-9 = 3(x² +8x+_16_)+21-48 = 2(x² +5/2x+_25/16_)+2-25/8
= (x+3)²-16 = 3(x+4) ²-27 = 2(x+5/4)²-9/8
-to find the final term of any of these equations: divide 2nd
term by 2 then square as shown
- if there is a coefficient, factor it out as shown above
- before putting in final term, you must multiply it by the coefficient
- remember, what you do on one side, you must do to the other side
6/2 = 3
3² = 9
factor 3 out
8/2 = 4
4² = 16
factor 2 out
5/2 divide by 2 = 5/4
5/4² = 25/16

16. Word Problems
Type One  good idea to draw a picture of some sort
A rectangular area is 600m. What are the dimensions of this area if
there is a definite wall?
A = lxw
= (600-2w)(w)
= 600w-2w²
= -2w² +600w
= -2(w²-300w+_22,500__)+45,000
= -2(w-150) ²+45, 000
W = 150
L = 600-2(150)
= 300m
W = 150m
- remember, factor out coefficient first
-divide second term by 2 then square to find the final term

17. Continued..
Type Two  make a table to help you
A company sells boots for $40, 600 people buy this product. For
every $10 increase, 60 fewer people buy the boots. What is the
maximum revenue?
Price: 40+10x
# Sold: 600-60x
40+10(3) = 70
600-60(3)= 420
(40+10x)(600-60x)
= 2400-2400x+6000-600²
= -600² + 3600x +2400
= -600(x²-6x + _9__)+24000 + 5400
= -600(x-3) ² +29 400
X = 3
http://www.sheepskin-boots-and-
slippers.com/images/discount-ugg-boots.jpg

18. Continued..
Type Three  the equation is always already given in the question
A soccer ball is thrown up in the air with an initial velocity of 120m/s.
Find the height of the ball and the time required with this equation:
H = -5t² +120t + 4
h= -5t²+120t+4
= -5(t² -24t+ _144_)4+720
= -5(t-12) ² +724
t= 12 seconds
h= 724 m
http://www.albion.edu/imsports/