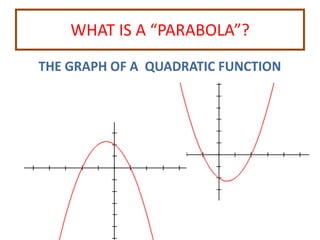
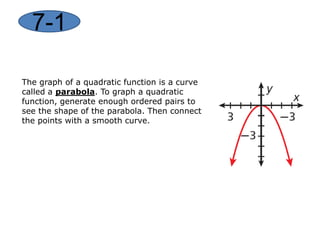
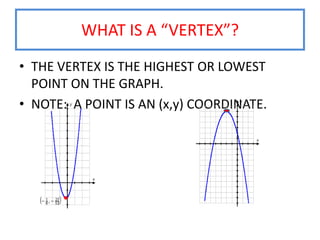
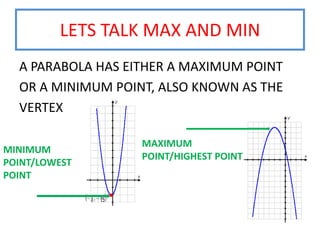
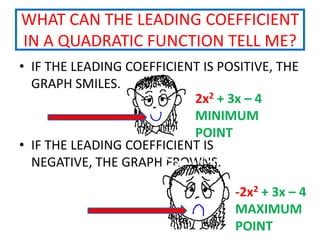
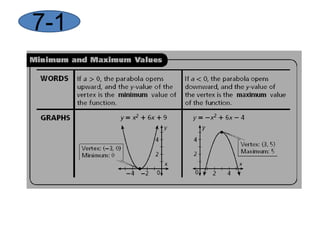
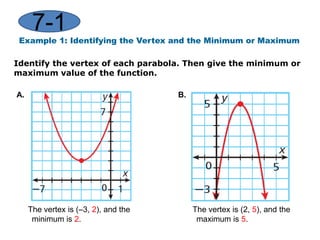
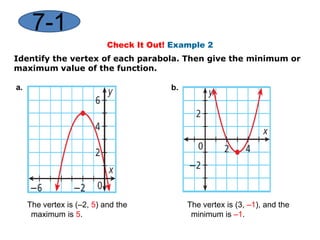
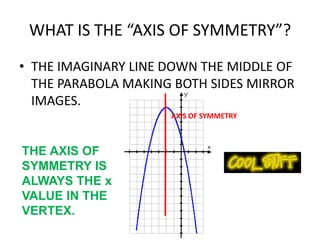
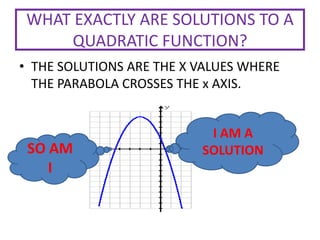
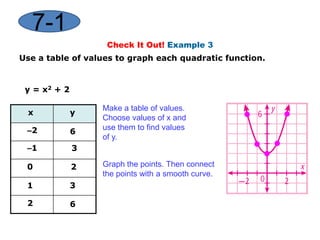
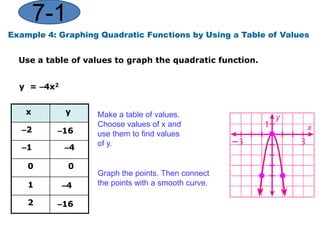
This document provides instruction on graphing quadratic functions. It defines key terms like parabola, vertex, axis of symmetry, and solutions. It explains that the vertex is the highest or lowest point and its x-coordinate is the axis of symmetry. The solutions are the x-values where the parabola crosses the x-axis. Examples show how to identify the vertex and whether the function has a maximum or minimum. The last example demonstrates graphing a quadratic function using a table of values.

1. x–2 –1 0 1 2 y632367-1PLUG IT IN, PLUG IT INWarm Up1. Evaluate x2 + 5x for x = 4 and x = –3. 36; –6 2. Generate ordered pairs for the function y = x2 + 2 with the given x VALUES. {–2, –1, 0, 1, 2}

2. QUADRATIC FUNCTIONSAND THEIR GRAPHSNC GOAL: 4.02 Graph, factor, and evaluate quadratic functions to solve problems. 7-1

3. ESSENTIAL QUESTIONSWHAT IS THE STANDARD FORM OF A QUADRATIC FUNCTION?

4. WHAT IS A “VERTEX”?

5. WHAT ROLE WOULD AN “AXIS OF SYMMETRY” PLAY?

6. HOW IMPORTANT ARE THE SOLUTIONS?

7. WHAT EXACTLY ARE SOLUTIONS TO A QUADRATIC FUNCTION?

8. WHAT IS A “PARABOLA”?

9. WHAT CAN THE LEADING COEFFICIENT IN A QUADRATIC FUNCTION TELL ME?7-1

10. VOCABULARYPARABOLAVERTEXSOLUTIONSAXIS OF SYMMETRYSTANDARD FORMMAXIMUMMINIMUM7-1

11. BLOOMSAnalysingComparingOrganisingDeconstructingAttributingOutliningFindingStructuringIntegrating7-1 Can you break information into parts to explore understandings and relationships?

12. TLWBATFIND THE VERTEX OF A QUADRATIC FUNCTION, AND IDENTIFY THE AXIS OF SYMMETRY AND SOLUTIONS.GRAPH A PARABOLA ON THE COORDINATE PLANE USING THE VERTEX, SOLUTIONS, AND OTHER ORDERED PAIRS.7-1

13. WHAT IS A “PARABOLA”?THE GRAPH OF A QUADRATIC FUNCTION

14. 7-1The graph of a quadratic function is a curve called a parabola. To graph a quadratic function, generate enough ordered pairs to see the shape of the parabola. Then connect the points with a smooth curve.

15. WHAT IS THE STANDARD FORM OF A QUADRATIC FUNCTION?ax2 + bx + c = 0BUTa= 0

16. WHAT IS A “VERTEX”?THE VERTEX IS THE HIGHEST OR LOWEST POINT ON THE GRAPH.NOTE: A POINT IS AN (x,y) COORDINATE.

17. LETS TALK MAX AND MINA PARABOLA HAS EITHER A MAXIMUM POINTOR A MINIMUM POINT, ALSO KNOWN AS THEVERTEXMAXIMUM POINT/HIGHEST POINTMINIMUM POINT/LOWEST POINT

18. WHAT CAN THE LEADING COEFFICIENT IN A QUADRATIC FUNCTION TELL ME?IF THE LEADING COEFFICIENT IS POSITIVE, THE GRAPH SMILES. IF THE LEADING COEFFICIENT IS NEGATIVE, THE GRAPH FROWNS.2x2 + 3x – 4MINIMUM POINT-2x2+ 3x – 4MAXIMUM POINT

19. 7-1

20. A.B.7-1Example 1: Identifying the Vertex and the Minimum or MaximumIdentify the vertex of each parabola. Then give the minimum or maximum value of the function.The vertex is (–3, 2), and the minimum is 2.The vertex is (2, 5), and the maximum is 5.

21. a.b.7-1Check It Out! Example 2 Identify the vertex of each parabola. Then give the minimum or maximum value of the function.The vertex is (3, –1), and the minimum is –1.The vertex is (–2, 5) and the maximum is 5.

22. WHAT IS THE “AXIS OF SYMMETRY”?THE IMAGINARY LINE DOWN THE MIDDLE OF THE PARABOLA MAKING BOTH SIDES MIRROR IMAGES.AXIS OF SYMMETRYTHE AXIS OF SYMMETRY IS ALWAYS THE x VALUE IN THE VERTEX.

23. WHAT EXACTLY ARE SOLUTIONS TO A QUADRATIC FUNCTION?THE SOLUTIONS ARE THE X VALUES WHERE THE PARABOLA CROSSES THE x AXIS.I AM A SOLUTIONSO AM I

24. A quick review on plotting pointsThe first number in an ordered pair is your x value and the second one is the y value.

25. Example: (2,3)x,yYou move left and right to graph an x value andup and down to graph a y value. Lets try a few.ALWAYS BEGIN FROM THE ORIGIN

26. http://mathforum.org/cgraph/cplane/pexample.htmlINTERACTIVE FUNhttp://www.webmath.com/gpoints.html7-1

27. TODAY WE WILL LEARN HOW TO FIND THE VERTEX IN THE CALCULATORLets use the function 3x2 + 5x + 5. Put this in your calculator under y=.

28. Push 2nd, trace, : notice #3 and 4? What does our graph have? Push 3 NOW IT GETS TRICKY

29. USE YOUR ARROWS TO MOVE TO THE LEFT OF THE VERTEX, STAY VERY CLOSE THOUGH, AND HIT ENTER. NOW MOVE TO THE RIGHT OF THE VERTEX, BUT STAY CLOSE, AND HIT ENTER 2 TIMES.

30. THE ORDERED PAIR AT THE BOTTOM OF THE SCREEN IS YOUR VERTEX.LETS TRY ANOTHER ONE-x2 + 4x + 3 does this graph have a minimumpoint or amaximum point?2nd, trace, 4, left bound, enter, right bound,enter enter. And the vertex is:(2,7)Be sure to put the vertex in parenthesis or it iswrong.

31. Now find the solutionsUse 2nd, trace, 5, enter, enter, enter. Find both of them and write them down. We can now graph this parabola with this information. But what if we needed a few more points to make a good graph.

32. If you push 2nd graph you will have a gozillion points to choose from. Pick a few.