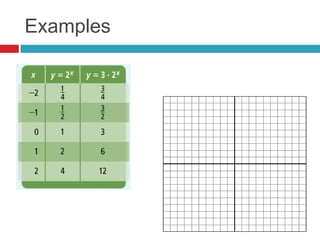
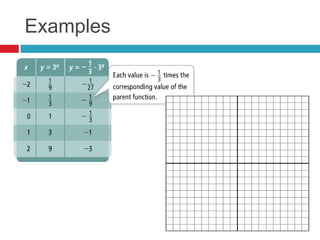
This document discusses properties and transformations of exponential functions, including stretch, compression, reflection, and horizontal and vertical translation. It also discusses the number e as the base for natural exponential functions and using the function A=Pe^rt to model continuously compounded interest. Examples are provided to demonstrate graphing transformations of exponential functions and using the continuously compounded interest formula.

1. 7.2 PROPERTIES OF
EXPONENTIAL
FUNCTIONS

2. Transformations of Exponential
Functions
Note that the base of the parent is a variable,
 Parent: therefore there are infinite “parents” within the
Exponential Family
 General Form:
 Stretch:
 Compression (shrink):
 Reflection:
 Horizontal Translation:
 Vertical Translation:

3. Graph each function as a
transformation of its parent
1. Create a Table of Values for the parent
2. Plot the points and label the graph
3. If the transformation contains a
stretch, compression, or reflection: Create a
Table of Values for the transformed function
(use the same x-values) and Plot the points
and label the graph
4. If the transformation contains a simple
horizontal or vertical translation: move the
parent points appropriately

4. Examples

5. Examples

6. Examples

7. The Number e
 The Number e is an irrational number
approximately equal to 2.71828
 Exponential functions with base e are called
natural base exponential functions.
 These exponential functions have the same
properties as other exponential functions
 To graph functions with base e, use the “e” key on
the calculator to get a decimal approximation

8. Continuously Compounded
Interest
To use this function:
1. Identify the value of the variables
2. Plug the known values into the equation
3. Solve for the unknown value

9. Example (p447)
Suppose you won a contest at the start of 5th
grade that deposited $3000 in an account that
pays 5% annual interest compounded
continuously. How much will you have in the
account when you enter high school 4 years
later? Express the answer to the nearest
dollar.

10. Homework
 P447 #1 – 4 all, 7 – 27 odd, 28 – 31 all