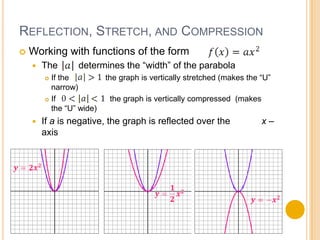
This document discusses quadratic functions and their transformations. It defines key terms like parabola, vertex, and axis of symmetry. The vertex form of a quadratic function makes it easy to identify transformations - the a value determines stretching or compression, the h value shifts the graph horizontally, and the k value shifts it vertically. For any quadratic function, the minimum or maximum value will occur at the vertex. Graphing involves plotting the vertex and axis of symmetry, then using a table of values. Writing quadratic functions starts with identifying the vertex coordinates, then using another point to solve for the a value.

1. CHAPTER 4 QUADRATIC FUNCTIONS
AND EQUATIONS
4.1 Quadratic Functions and Transformations

2. DEFINITIONS
 A parabola is the graph of a quadratic function.
 A parabola is a “U” shaped graph
 The parent Quadratic Function is
Vertex at (0, 0)
Axis of Symmetry at x = 0

3. DEFINITIONS
 The vertex form of a quadratic function makes it
easy to identify the transformations
 The axis of symmetry is a line that divides the
parabola into two mirror images (x = h)
 The vertex of the parabola is (h, k) and it
represents the intersection of the parabola and the
axis of symmetry.

4. REFLECTION, STRETCH, AND COMPRESSION
 Working with functions of the form
 The determines the “width” of the parabola
 If the the graph is vertically stretched (makes the “U”
narrow)
 If the graph is vertically compressed (makes
the “U” wide)
 If a is negative, the graph is reflected over the x–
axis

5. MINIMUM AND MAXIMUM VALUES
 The minimum value of a function is the least y –
value of the function; it is the y – coordinate of the
lowest point on the graph.
 The maximum value of a function is the greatest
y – value of the function; it is the y–
coordinate of the highest point on the graph.
 For quadratic functions the minimum or maximum
point is always the vertex, thus the minimum or
maximum value is always the y – coordinate
of the vertex

6. TRANSFORMATIONS – USING VERTEX FORM
 Remember transformations from Chapter 2
 The vertex form makes identifying transformations
easy
 a gives you information about stretch, compression, and
reflection over the x – axis
 h gives you information about the horizontal shift
 k gives you information about the vertical shift
 The vertex is at (h, k)
 The axis of symmetry is at x = h

7. TRANSFORMATIONS – USING VERTEX FORM
Graphing Quadratic Functions:
1. Identify and Plot the vertex and axis of symmetry
2. Set up a Table of Values. Choose x – values to the
right and left of the vertex and find the
corresponding y – values
3. Plot the points and sketch the parabola

8. EXAMPLE: GRAPH EACH FUNCTION. DESCRIBE
HOW IT WAS TRANSLATED FROM

9. EXAMPLE: GRAPH EACH FUNCTION. DESCRIBE
HOW IT WAS TRANSLATED FROM

10. EXAMPLE: GRAPH EACH FUNCTION. DESCRIBE
HOW IT WAS TRANSLATED FROM

11. EXAMPLE: GRAPH EACH FUNCTION. DESCRIBE
HOW IT WAS TRANSLATED FROM

12. TRANSFORMATIONS – USING VERTEX FORM
Writing the equations of Quadratic Functions:
1. Identify the vertex (h, k)
2. Choose another point on the graph (x, y)
3. Plug h, k, x, and y into and
solve for a
4. Use h, k, and a to write the vertex form of the
quadratic function

13. EXAMPLE: WRITE A QUADRATIC FUNCTION TO
MODEL EACH GRAPH

14. EXAMPLE: WRITE A QUADRATIC FUNCTION TO
MODEL EACH GRAPH