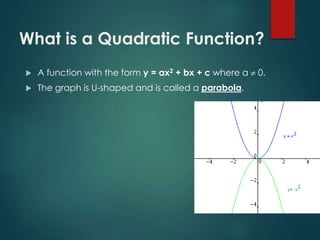
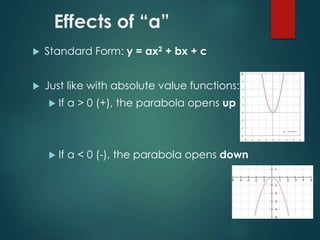
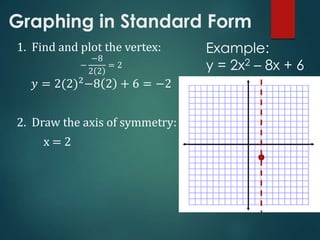
Quadratic functions are modeled by the equation y = ax^2 + bx + c, where a ≠ 0. They produce U-shaped parabolic graphs. Many real-world phenomena follow quadratic patterns, like water in a fountain or a basketball's trajectory. The lowest or highest point on a parabola is the vertex. To graph a quadratic function in standard form, you first find the vertex by calculating -b/2a, then plot the axis of symmetry and other points to sketch the parabolic curve.

1. Basics of Graphing
Quadratic Functionsadapted from hisema01

2. What is a Quadratic Function?
 A function with the form y = ax2 + bx + c where a  0.
 The graph is U-shaped and is called a parabola.

3. Why Study Quadratics?
 Many things we see every day are modeled by
quadratic functions.
 What are some examples?
 Water in a drinking fountain
 The McDonald’s Golden Arches
 The path of a basketball

4. Quadratic Vocab
 The lowest or highest point is called the vertex.
 The axis of symmetry is a vertical line through the vertex.

5. Effects of “a”
 Standard Form: y = ax2 + bx + c
 Just like with absolute value functions:
 If a > 0 (+), the parabola opens up
 If a < 0 (-), the parabola opens down

6. Effects of “a”
 Standard Form: y = ax2 + bx + c
 Just like with absolute value functions:
 If |a| < 1, the parabola is wider than y = x2
because it’s vertically shrunk
 If |a| > 1, the parabola is narrower than
y = x2 because it’s vertically stretched.

7. Effects of “c”
 Standard Form: y = ax2 + bx + c
 Just like with absolute value functions:
 If c < 1, the parabola is shifted down c units
 If c > 1, the parabola is shifted up c units

8. Finding the Vertex
 The x-coordinate of the vertex is −
𝑏
2𝑎
 To find the y, plug the x-coordinate into the equation.
 Axis of symmetry is the line x = −
𝑏
2𝑎

9. Graphing in Standard Form
1. Find and plot the vertex:
−
−8
2 2
= 2
𝑦 = 2(2)2−8 2 + 6 = −2
2. Draw the axis of symmetry:
x = 2
Example:
y = 2x2 – 8x + 6

10. Graphing in Standard Form
3. Choose two x values on one
side and plot the points.
x y
3 0
4 6
4. Use symmetry to plot two
points on the other side.
5. Lastly, you should connect
the points with a curve
(parabola).
Example:
y = 2x2 – 8x + 6