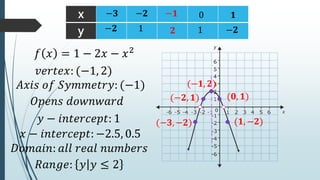
This document discusses quadratic functions and their graphs. It defines key features of quadratic graphs including the vertex, axis of symmetry, and effect of coefficients on the opening of the parabola. Examples are provided to demonstrate how to identify these features from the equation, generate tables of values, and graph the quadratic function. Learning targets are outlined to draw and analyze quadratic graphs and the effect of changing coefficients on the graph.

1. Forms of Quadratic Functions
Give the different forms of
quadratic function, determine the
axis of symmetry, opening of the
parabola and the vertex; and
Identify the different forms of
quadratic functions.

2. The vertex is (h,k), and the axis of
symmetry is x = h which divides the
graph of quadratic function into two
equal parts. The value of a indicates
the opening of the graph. If the value
of a is positive, the graphs opens
upward. If the value of a is negative,
the graph opens downward.

3. To find the value of the vertex use the
formula of:
𝒉 =
−𝒃
𝟐𝒂
and 𝒌 =
𝟒𝒂𝒄−𝒃𝟐
𝟒𝒂
and the axis of
symmetry is x = h.

4. Examples:
1.y = 3x² - 4
2.y = - x² + 2x + 3
3.y = 5x²
4.y = 2x² + 8x + 16

5. Graphs of Quadratic
Functions

6. Learning Targets
 Draw the graphs of the quadratic
function;
 Analyze the effect of changing the
values of a, h and k in the equation
y = a(x-h)²+k of the quadratic function
on its graph.

7. GRAPHS OF QUADRATIC FUNCTION
All quadratic functions have graphs
similar to this graph. This U-shaped is
called a parabola. 𝑷𝒂𝒓𝒂𝒃𝒐𝒍𝒂
𝒗𝒆𝒓𝒕𝒆𝒙
( 0, -1 )
The “turning points” of the graph is
called the vertex of the parabola.
The parabola is symmetric with respect
to a line that passes through the vertex.
This line is called the axis of symmetry. It
divides the parabola into two parts so
that one part is a reflection of the other
part.
𝒂𝒙𝒊𝒔 𝒐𝒇 𝒔𝒚𝒎𝒎𝒆𝒕𝒓𝒚

8. EXAMPLE 1. Construct a table of values for the
quadratic function and identify at least five points of
the function.
𝑓 𝑥 = 1 − 2𝑥 − 𝑥2
𝒌 =
𝟒𝒂𝒄 − 𝒃𝟐
𝟒𝒂
𝒉 =
−𝒃
𝟐𝒂
𝒂 = −𝟏 𝒃 = −𝟐 𝒄 = 𝟏
𝑭𝒊𝒏𝒅 𝒕𝒉𝒆 𝒗𝒆𝒓𝒕𝒆𝒙.
𝒉 =
−(−𝟐)
𝟐(−𝟏)
𝒉 =
𝟐
−𝟐
𝒉 = −𝟏
𝒌 =
−𝟒 − 𝟒
−𝟒
𝒌 =
𝟒(−𝟏)(𝟏) − (−𝟐)𝟐
𝟒(−𝟏)
𝒌 =
−𝟖
−𝟒
𝒌 = 𝟐
𝑽𝒆𝒓𝒕𝒆𝒙: (−1, 2)

9. x
y
−𝟏
𝟐
−𝟐
−𝟑 0 𝟏
1
−𝟐 1 −𝟐
𝑓 𝑥 = 1 − 2(−2) − (−2)2
𝒙 = −𝟐
𝑓 𝑥 = 1 − 2𝑥 − 𝑥2
𝑓 𝑥 = 1
𝑓 𝑥 = 1 + 4 − 4
𝑓 𝑥 = 1 − 2(−3) − (−3)2
𝒙 = −𝟑
𝑓 𝑥 = −2
𝑓 𝑥 = 1 + 6 − 9
𝑓 𝑥 = 1 − 2(0) − (0)2
𝒙 = 𝟎
𝑓 𝑥 = 1
𝑓 𝑥 = 1 − 0 − 0
𝑓 𝑥 = 1 − 2(1) − (1)2
𝒙 = 𝟏
𝑓 𝑥 = −2
𝑓 𝑥 = 1 − 2 − 1
𝑽𝒆𝒓𝒕𝒆𝒙: (−1, 2)

10. x
y
−𝟏
(−𝟏, 𝟐)
−𝟐
−𝟑 0 𝟏
1
−𝟐 1 −𝟐
𝑓 𝑥 = 1 − 2𝑥 − 𝑥2
𝑣𝑒𝑟𝑡𝑒𝑥: (−1, 2)
𝟐
(−𝟐, 𝟏)
(−𝟑, −𝟐) (𝟏, −𝟐)
(𝟎, 𝟏)
𝐴𝑥𝑖𝑠 𝑜𝑓 𝑆𝑦𝑚𝑚𝑒𝑡𝑟𝑦: (−1)
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 1
𝑂𝑝𝑒𝑛𝑠 𝑑𝑜𝑤𝑛𝑤𝑎𝑟𝑑
𝑥 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: −2.5, 0.5
𝑅𝑎𝑛𝑔𝑒: 𝑦 𝑦 ≤ 2
𝐷𝑜𝑚𝑎𝑖𝑛: 𝑎𝑙𝑙 𝑟𝑒𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠

11. EXAMPLE 2. Draw the graph of the quadratic
function.
𝑦 = −𝑥2
− 2𝑥 + 3
𝒌 =
𝟒𝒂𝒄 − 𝒃𝟐
𝟒𝒂
𝒉 =
−𝒃
𝟐𝒂
𝒂 = −𝟏 𝒃 = −𝟐 𝒄 = 𝟑
𝑭𝒊𝒏𝒅 𝒕𝒉𝒆 𝒗𝒆𝒓𝒕𝒆𝒙.
𝒉 =
−(−𝟐)
𝟐(−𝟏)
𝒉 =
𝟐
−𝟐
𝒉 = −𝟏 𝒌 =
−𝟏𝟐 − 𝟒
−𝟒
𝒌 =
𝟒(−𝟏)(𝟑) − (−𝟐)𝟐
𝟒(−𝟏)
𝒌 =
−𝟏𝟔
−𝟒
𝒌 = 𝟒
𝑽𝒆𝒓𝒕𝒆𝒙: (−1, 4)

12. x
y
−𝟏
𝟒
−𝟐
−𝟑 0 𝟏
3
𝟎 3 𝟎
𝑓 𝑥 = −(0)2 − 2 0 + 3
𝒙 = −𝟐
𝑦 = −𝑥2
− 2𝑥 + 3
𝑓 𝑥 = 3
𝒙 = −𝟑
𝑓 𝑥 = 0
𝒙 = 𝟎
𝑓 𝑥 = 3
𝒙 = 𝟏
𝑓 𝑥 = 0
𝑓 𝑥 = 0 − 0 + 3
𝑓 𝑥 = −(−3)2
− 2 −3 + 3
𝑓 𝑥 = −9 + 6 + 3
𝑓 𝑥 = −(−2)2 − 2 −2 + 3
𝑓 𝑥 = −4 + 4 + 3
𝑓 𝑥 = −(1)2 − 2 1 + 3
𝑓 𝑥 = −1 − 2 + 3

13. x
y
−𝟏
(−𝟏, 𝟒)
−𝟐
−𝟑 0 𝟏
3
𝟎 3 𝟎
𝑦 = −𝑥2
− 2𝑥 + 3
𝑣𝑒𝑟𝑡𝑒𝑥: (−1, 4)
𝟒
(−𝟐, 𝟑)
(−𝟑, 𝟎) (𝟏, 𝟎)
(𝟎, 𝟑)
𝐴𝑥𝑖𝑠 𝑜𝑓 𝑆𝑦𝑚𝑚𝑒𝑡𝑟𝑦: (−1)
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 3
𝑂𝑝𝑒𝑛𝑠 𝑑𝑜𝑤𝑛𝑤𝑎𝑟𝑑
𝑥 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: −3 𝑎𝑛𝑑 1
𝑅𝑎𝑛𝑔𝑒: 𝑦 𝑦 ≤ 4
𝐷𝑜𝑚𝑎𝑖𝑛: 𝑎𝑙𝑙 𝑟𝑒𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠

14. EXAMPLE 3. Draw the graph of the quadratic
function.
𝑦 = (𝑥 − 2)2
− 4
𝑭𝒊𝒏𝒅 𝒕𝒉𝒆 𝒗𝒆𝒓𝒕𝒆𝒙.
𝒉 = 𝟐 𝒌 = −𝟒
𝑽𝒆𝒓𝒕𝒆𝒙: (2, −4)
𝒇 𝒙 = 𝒂(𝒙 − 𝒉)𝟐
+ 𝒌
𝑦 = (𝑥 − 2)2
− 4

15. x
y
2
−𝟒
1
0 3 𝟒
−3
𝟎 −3 𝟎
𝒙 = 𝟏
𝑦 = (−1)2
− 4
𝑓 𝑥 = −3
𝒙 = 𝟎
𝑓 𝑥 = 0
𝒙 = 𝟑
𝑓 𝑥 = −3
𝒙 = 𝟒
𝑓 𝑥 = 0
𝑦 = (𝑥 − 2)2
− 4
𝑦 = (1 − 2)2
− 4
𝑦 = (−2)2
− 4
𝑦 = (0 − 2)2
− 4
𝑦 = (1)2
− 4
𝑦 = (3 − 2)2
− 4
𝑦 = (2)2
− 4
𝑦 = (4 − 2)2
− 4

16. (𝟒, 𝟎)
𝑦 = (𝑥 − 2)2
− 4
𝑣𝑒𝑟𝑡𝑒𝑥: (2, −4)
(𝟏, −𝟑)
(𝟎, 𝟎)
(𝟑, −𝟑)
(𝟐, −𝟒)
𝐴𝑥𝑖𝑠 𝑜𝑓 𝑆𝑦𝑚𝑚𝑒𝑡𝑟𝑦: (2)
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 0
𝑂𝑝𝑒𝑛𝑠 𝑢𝑝𝑤𝑎𝑟𝑑
𝑥 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 0 𝑎𝑛𝑑 4
𝑅𝑎𝑛𝑔𝑒: 𝑦 𝑦 ≥ −4
𝐷𝑜𝑚𝑎𝑖𝑛: 𝑎𝑙𝑙 𝑟𝑒𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠
x
y
2
−𝟒
1
0 3 𝟒
−3
𝟎 −3 𝟎

17. Generate a table of values and graph each quadratic functions and
determine the vertex, axis of symmetry, y- and x- intercepts, maximum
or minimum value, opening of parabola, range, and domain.
NOTE: Use GRAPHING PAPER for your graph and other
paper for the table of values.
1. 𝒚 = 𝒙𝟐 + 𝒙 − 𝟒
2. 𝒚 = 𝒙𝟐
− 𝟑𝒙 − 𝟒
3. 𝒚 = 𝟐(𝒙 − 𝟏)𝟐 + 𝟑
4. 𝒚 = (𝒙 − 𝟑)𝟐 + 𝟐