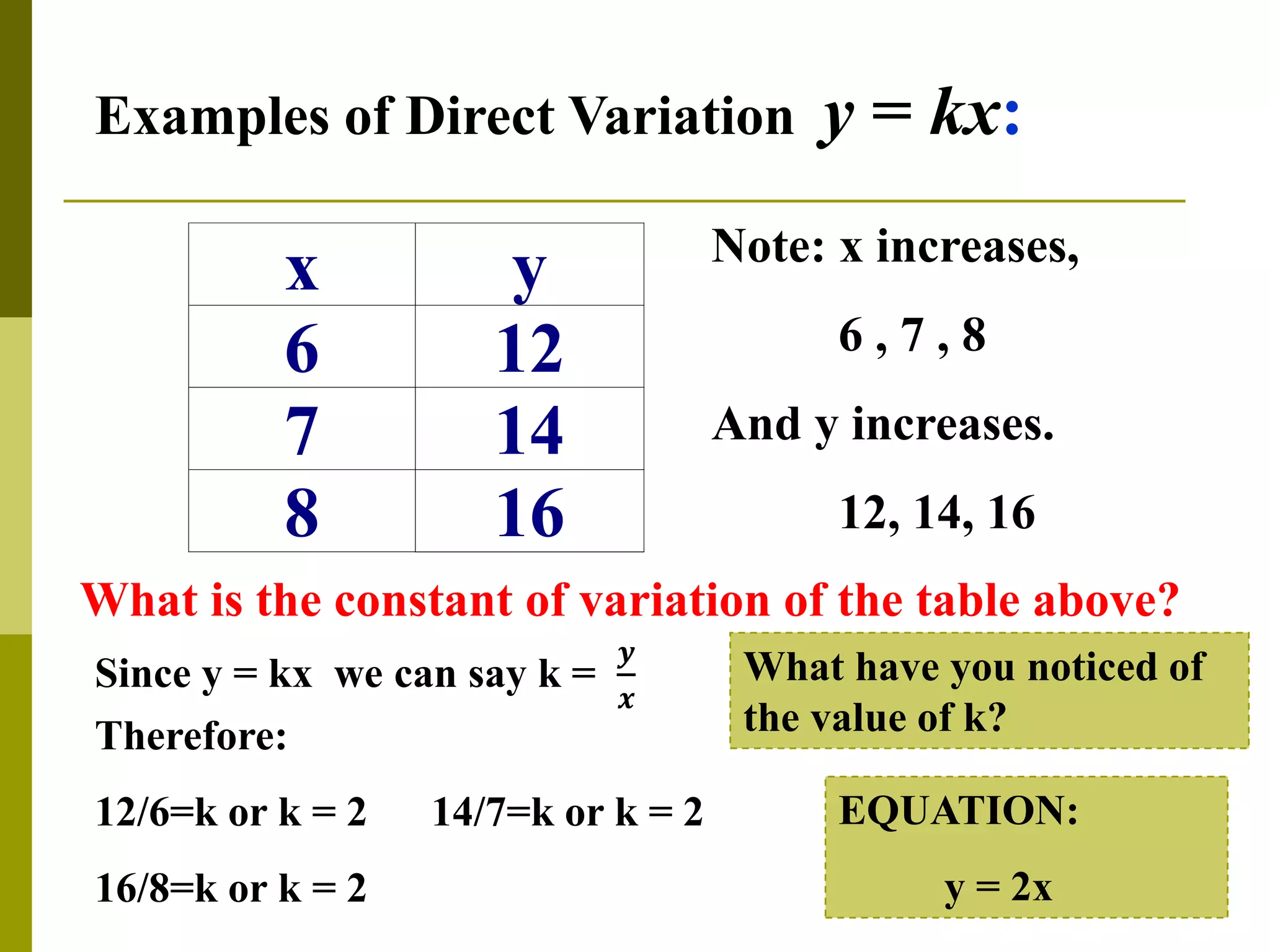
This document discusses direct variation and provides examples to illustrate the concept. Direct variation means that as one variable (the independent variable) increases or decreases, the other variable (the dependent variable) also increases or decreases by a constant factor. The constant factor is called the constant of variation. Several examples of direct variation relationships in tables and graphs are presented, along with exercises for students to practice determining if a relationship demonstrates direct variation and identifying the constant of variation. Word problems involving direct variation are also presented and solved step-by-step.

1. ACTIVITY:
“Agree or
disagree , that is
the question!”

2. Do you Agree?
 The more time I drive (at a
constant rate), the more distance
I cover.
 If you increase a recipe for more
people, the more of ingredients
you need.
 (In a computer shop)The more
hours you play online games, the
more money you pay.

3. Do you Agree?
 The more apparels I purchase, the
more money it costs.
 The less time you study, the lower
scores you will get in the exam.
 The less water you drink, the less
trips to the bathroom you have to
make.
 The more time you play temple run,
the longer your cellphone battery
stays.

4. Do you Agree?
 The more time I drive (at a
constant rate), the more distance
I cover.
 If you increase a recipe for more
people, the more of ingredients
you need.
 (In a computer shop)The more
hours you play online games, the
more money you pay.

5. Do you Agree?
 The more apparels I purchase, the
more money it costs.
 The less time you study, the lower
scores you will get in the exam.
 The less water you drink, the less
trips to the bathroom you have to
make.
 The more time you play temple run,
the longer your cellphone battery
stays.

6. Direct Variation
What …
Know:__________________
Want to learn: ___________
Had learned:_____________

7. Definition: y varies
directly as x means that y = kx where y is the
dependent variable, x is the independent
variable and k is the constant of variation.
In other words:
* As x increases in value, y increases or
* As x decreases in value, y decreases.
Direct Variation
Another way of writing this is k =
𝒚
𝒙

8. Examples of Direct Variation y = kx:
x y
6 12
7 14
8 16
Note: x increases,
6 , 7 , 8
And y increases.
12, 14, 16
What is the constant of variation of the table above?
Since y = kx we can say k =
𝒚
𝒙
Therefore:
12/6=k or k = 2 14/7=k or k = 2
16/8=k or k = 2
EQUATION:
y = 2x
What have you noticed of
the value of k?

9. x y
10 30
5 15
3 9
Note: x decreases,
10, 5, 3
And y decreases.
30, 15, 9
What is the constant of variation of the table above?
Since y = kx we can say k =
𝒚
𝒙
30/10 = k or k = 3 15/5=k or k = 3
9/3 = k or k =3
y = 3x is the
equation
Examples of Direct Variation y = kx:
What have you noticed
of the value of k?

10. Note: x decreases,
-4, -16, -40
And y decreases.
-1, -4, -10
What is the constant of variation of the table above?
Since y = kx we can say k =
𝒚
𝒙
-1/-4=k or k = ¼ -4/-16=k or k = ¼
-10/-40=k or k = ¼
y = ¼ x is the
equation!
Examples of Direct Variation:
What have you noticed
of the value of k?
x y
-4 -1
-16 -4
-40 -10

11. What is the constant of variation
for the following direct variation?
Answer
Now
1. 2
2. -2
3. -½
4. ½
x y
4 -8
8 -16
-6 12
3 -6

12. Is this a direct variation? If yes, give the
constant of variation (k) and the equation.
Yes!
k = 6/4 or 3/2
Equation?
y = 3/2 x
x y
4 6
8 12
12 18
18 27

13. Yes!
k = 25/10 or 5/2
k = 10/4 or 5/2
Equation?
y = 5/2 x
Is this a direct variation? If yes, give the
constant of variation (k) and the equation.
x y
10 25
6 15
4 10
2 5

14. X Y
15 5
3 26
1 75
2 150
No!
The k values are
different!
Is this a direct variation? If yes, give the
constant of variation (k) and the equation.

15. Which of the following is a direct
variation?
1. A
2. B
3. C
4. D
Answer
Now

16. Which equation describes the
following table of values?
1. y = -2x
2. y = 2x
3. y = ½ x
4. xy = 200
Answer
Now
x y
10 5
2 1
12 6
20 10

17. Using Direct Variation to find unknowns (y = kx)
Given that y varies directly with x, and y = 28 when
x=7, Find x when y = 52. HOW???
2 -step process
x y
7 28
? 52
1. Find the constant variation
k = y/x or k = 28/7 = 4
k = 4
2. Use y = kx. Find the unknown (x).
52 = 4x or 52/4 = x
x = 13
Therefore:
x =13 when y = 52

18. Given that y varies directly with x, and y = 3 when
x = 9, Find y when x = 40.5. HOW???
2 - step process x y
9 3
40.5 ?
1. Find the constant variation.
k = y/x or k = 3/9 = 1/3
k = 1/3
2. Use y = kx. Find the unknown (x).
y = (1/3)40.5
y= 13.5
Therefore:
x = 40.5 when y = 13.5
Using Direct Variation to find unknowns (y = kx)

19. Given that y varies directly with x, and y = 6 when
x = -5, Find y when x = - 8. HOW???
2 - step process
x y
-5 6
-8 ?
1. Find the constant variation.
k = y/x or k = 6/-5 = -1.2
k = -1.2
2. Use y = kx. Find the unknown (x).
y= -1.2(-8)
x= 9.6
Therefore:
x = -8 when y = 9.6
Using Direct Variation to find unknowns (y = kx)

20. Using Direct Variation
to solve word problems
Problem:
A car uses 8 liters of gasoline
to travel 160 km. How much
gasoline will the car use to
travel 400 km?
Step One:
Find points in table
x (gas) y (km)
8 160
? 400
Step Two: Find the constant
variation and equation:
k = y/x or k = 160/8 or 20
Equation: y = 20 x
Step Three: Use the equation
to find the unknown.
400 = 20x
400 = 20x
20 20
or x = 20 liters

21. Using Direct Variation
to solve word problems
Step One:
Find points in table
Alternative Solution:
Step Three:
Solve for the unknown
160
8
=
400
𝑥
160x = 8(400)
or 20 lit.𝑥 =
8(400)
160
Problem: A car uses 8 liters of
gasoline to travel 160 km.
How much gasoline will the
car use to travel 400 km?
x (gas) y (km)
8 160
? 400
Where: x1 = 8, y1 = 160
x2 = ? y2 = 400
Step Two: Form a proportion
Since k1 = k2
𝑦1
𝑥1
=
𝑦2
𝑥2

22. Step One: Find points in table.
Step Two: Find the constant
variation.
k =
𝑦
𝑥
k =
1000
5
= 200
Step Three:
Use the equation to find the unknown
y = k(x)
y = 200(30) or y = 6000
Using Direct Variation
to solve word problems
Problem:
Julio’s wages vary
directly as the number of hours
that he works. If his wag for 5
hours is P1000, how much will
there be in 30 hours?
X (hours) Y (wages)
5 1000
30 ?

23. Using Direct Variation
to solve word problems
Problem:
Julio’s wages vary directly as the number
of hours that he works. If his wage for
5 hours is P1000, how much will there be
in 30 hours?
Use the proportion and solve for the
unknown:
Alternative Method
or
𝑥1
𝑦1
=
𝑥2
𝑦2

24. EXERCISES: Work as a group, evaluate
and present your answers on the board.
Refer to ACTIVITY 6: Learner’s Manual,
pp. 200 - 202
GROUP 1: A. 1- 2, B. 1, C. 1-2, D. 1
GROUP 2: A. 3 - 4, B. 2, C. 3 - 4, D. 2
GROUP 3: A. 5 - 6, B. 3, C. 5 - 6, D. 3
GROUP 4: A. 7 - 8, B. 4, C. 7 - 8, D. 4
GROUP 5: A. 9 - 10, B. 5, C. 9 - 10, D. 5

25. Reflect:
How did you find the activity?
What were the problems encountered
in working with the group activity?
How were you able to manage and
mitigate the circumstances you’ve
encountered?

26. ASSIGNMENT:
A. Choose and evaluate 3 odd problems if your first
name starts with a vowel, otherwise, choose 3 even
numbers if your first name starts with consonant.
Reference: LM, p. 203
B. Make a narrative of your inspiring experience
where knowledge of direct proportion guided and
molded you to be a better individual.
Be ready to share next meeting.

27. End