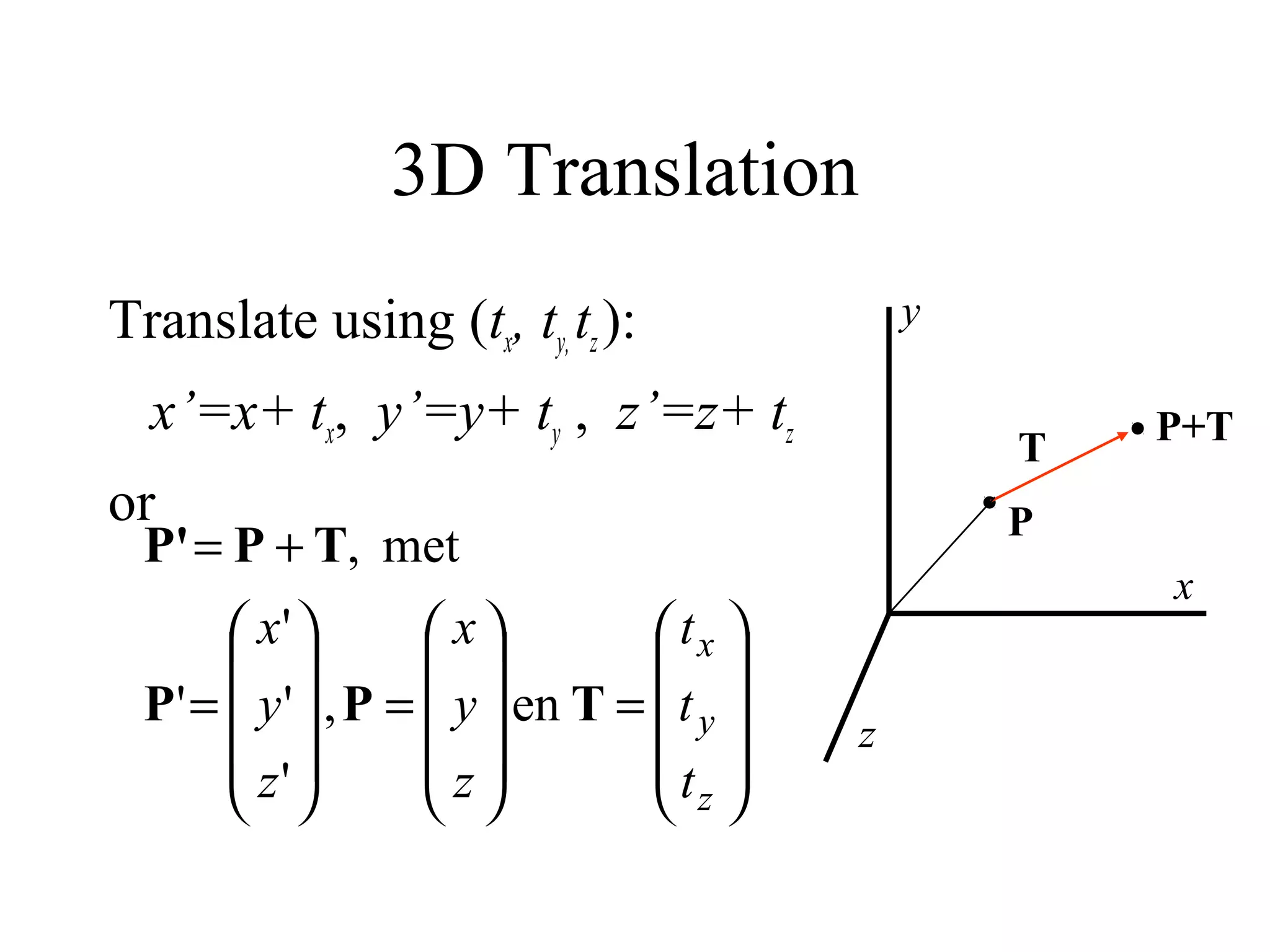
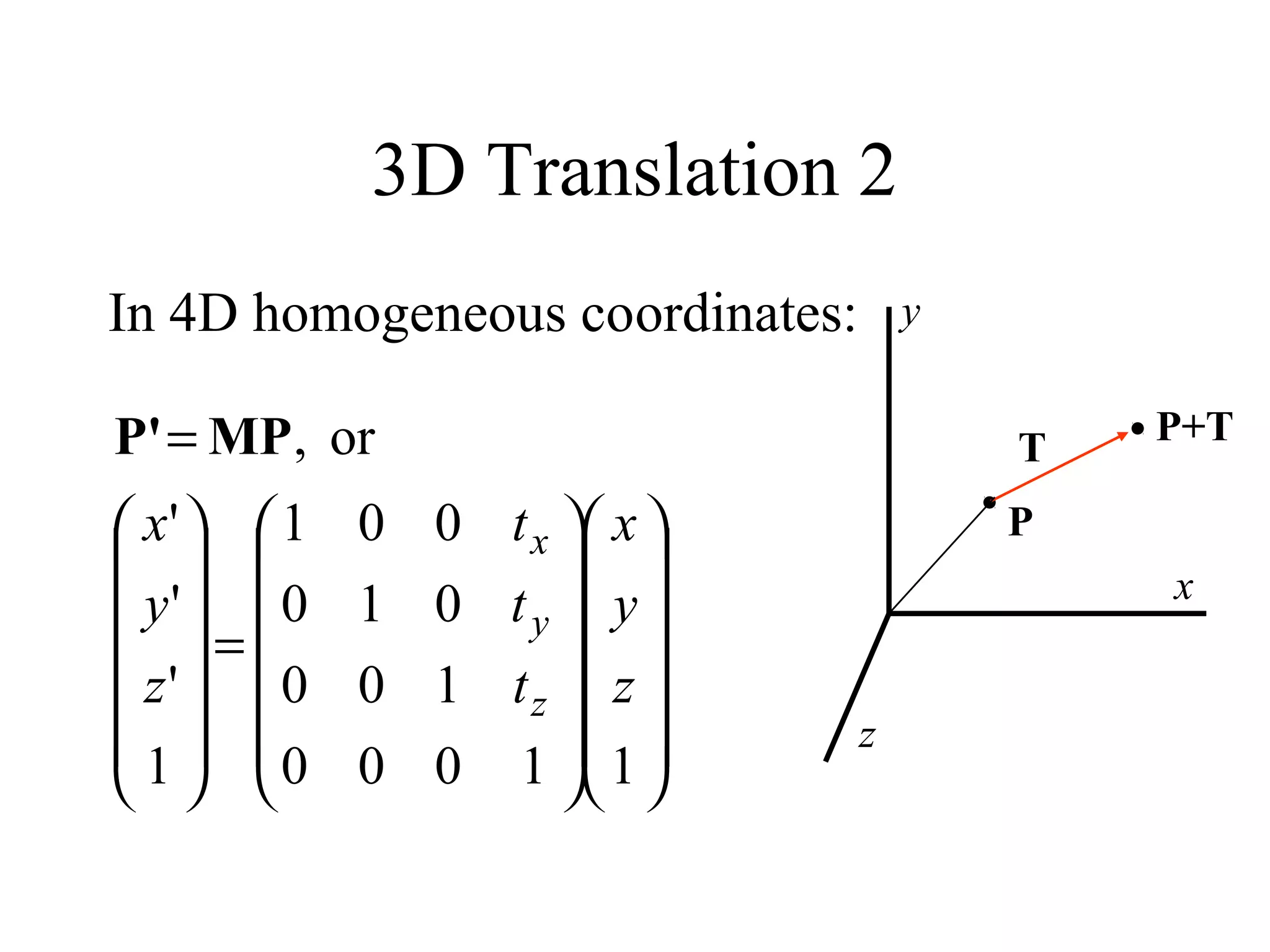
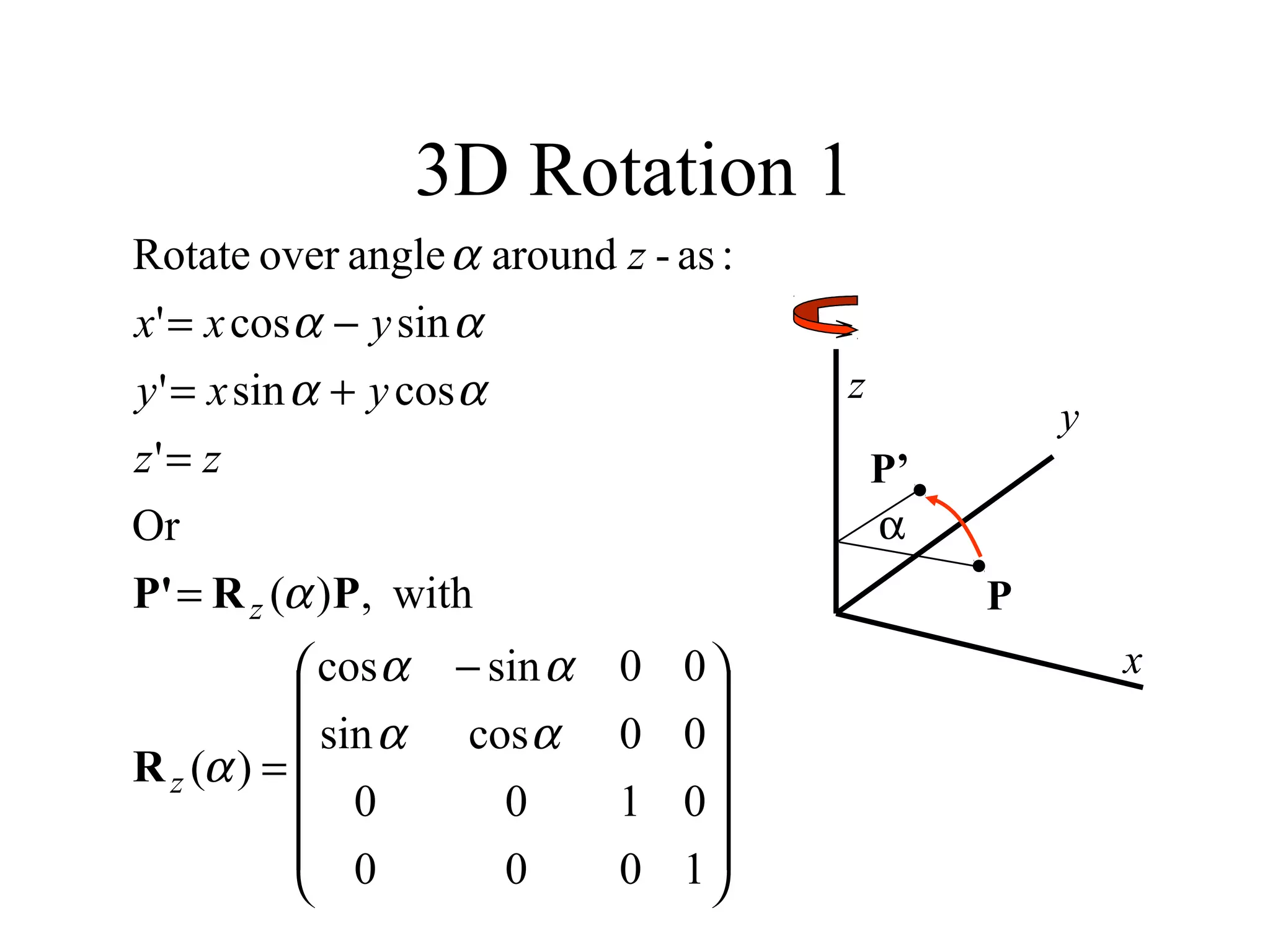
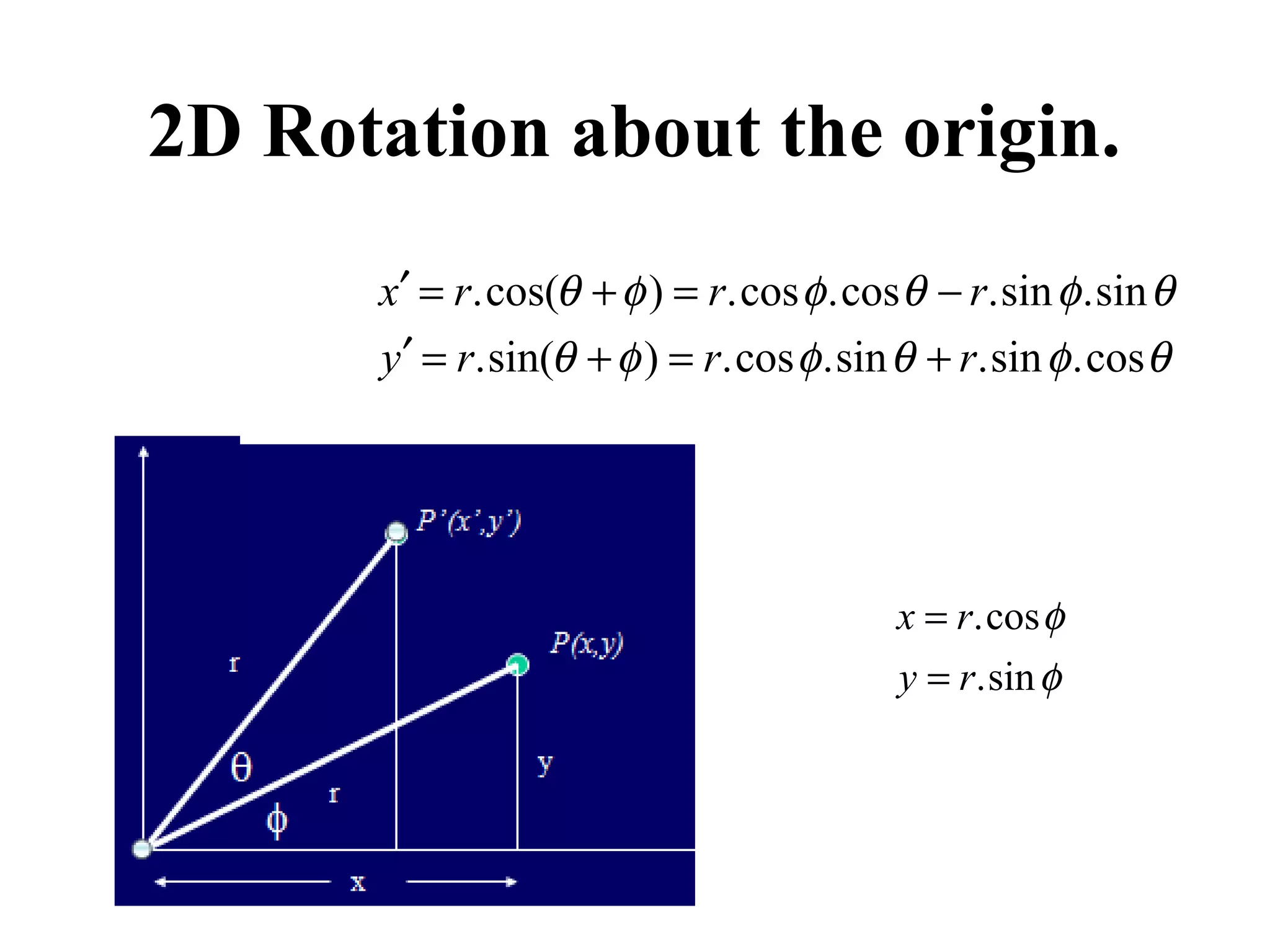
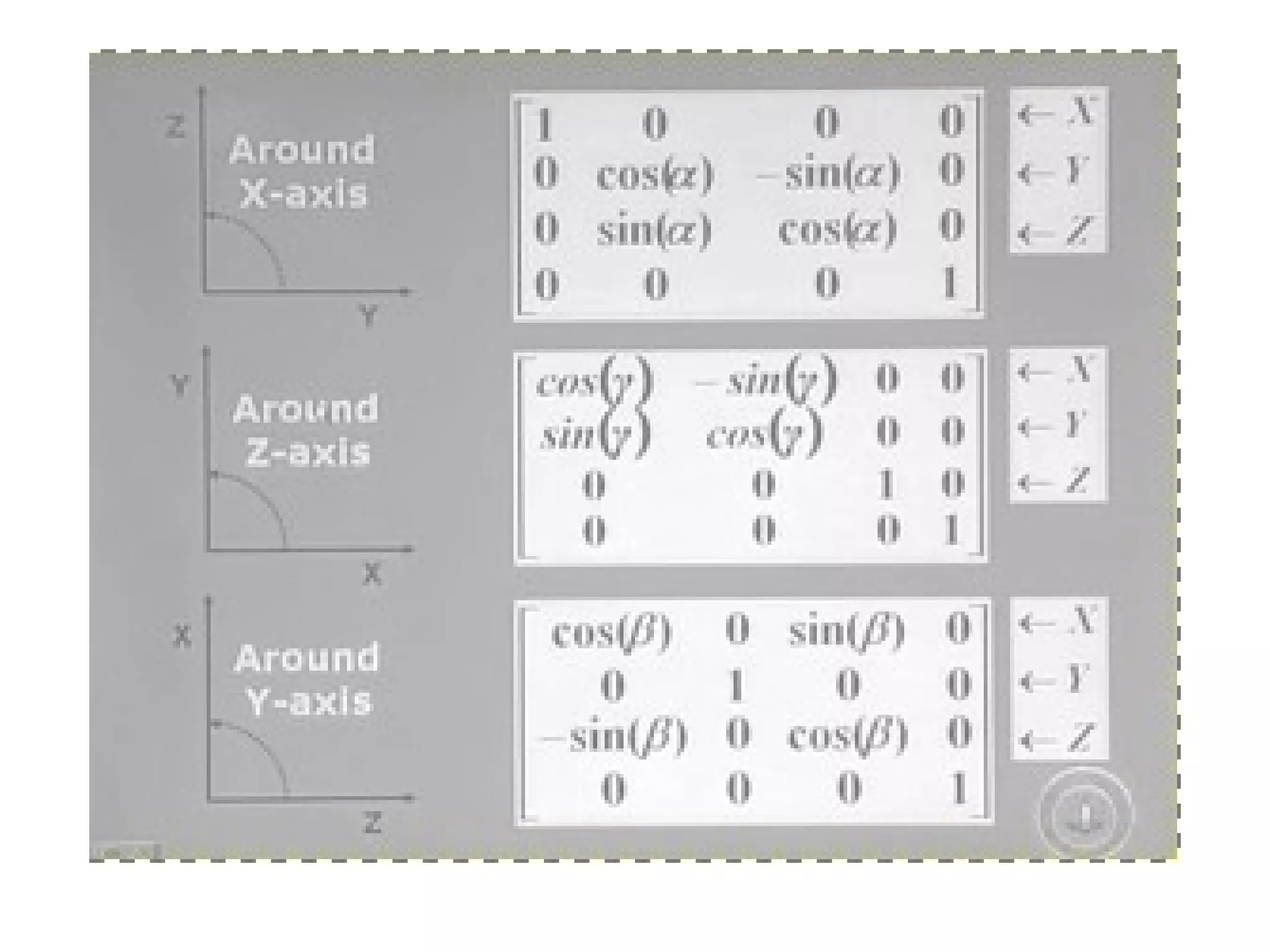
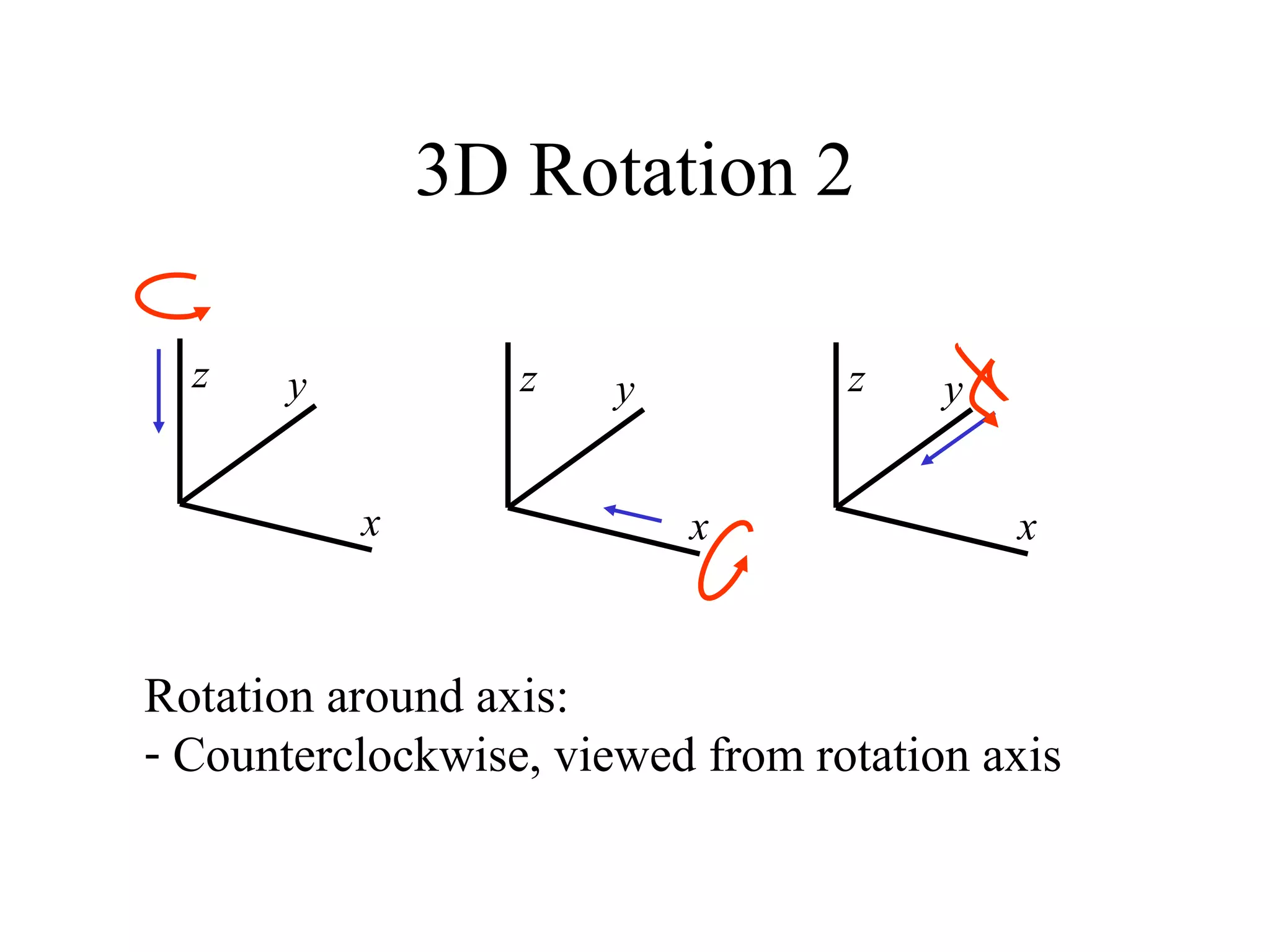
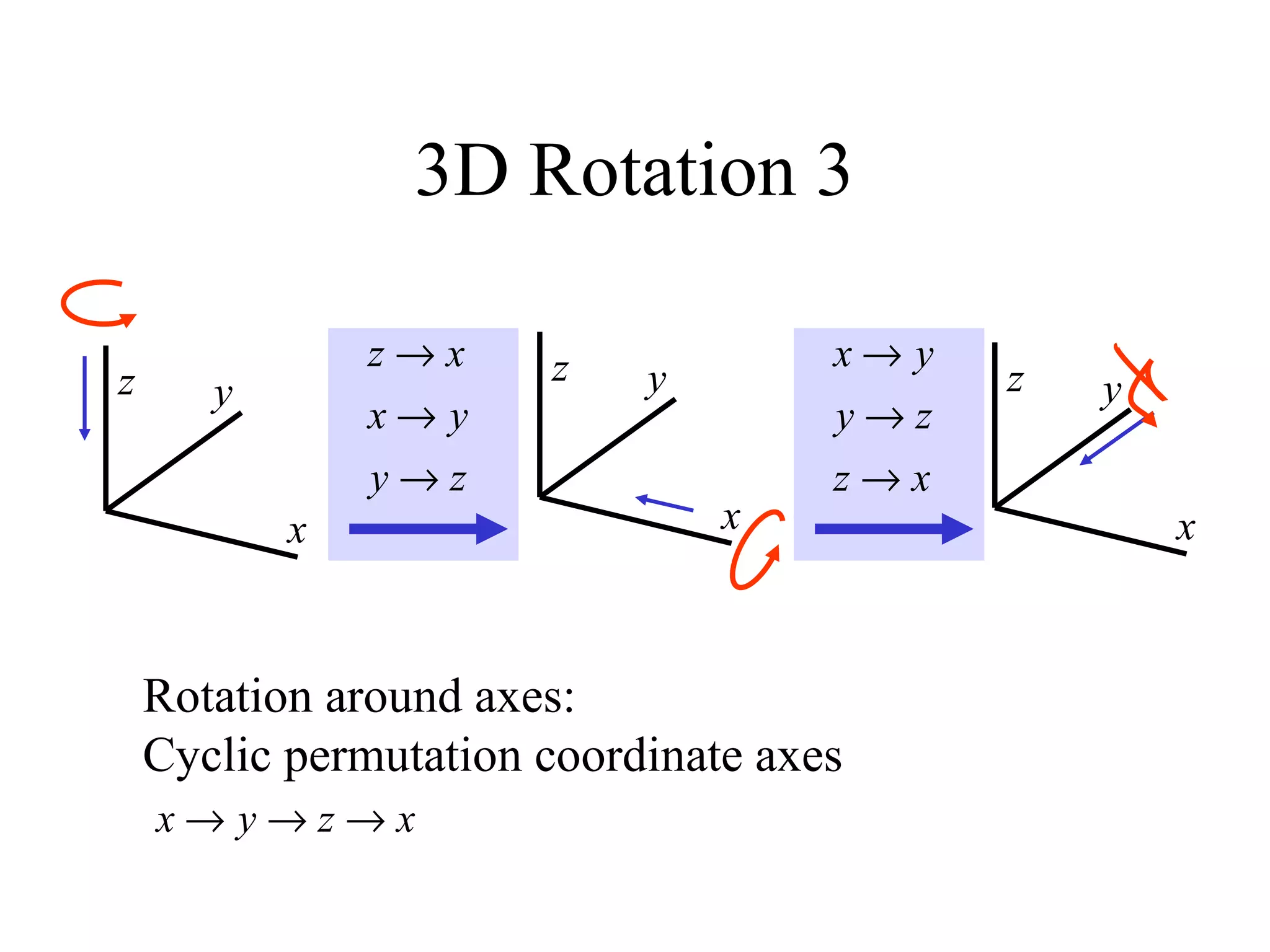
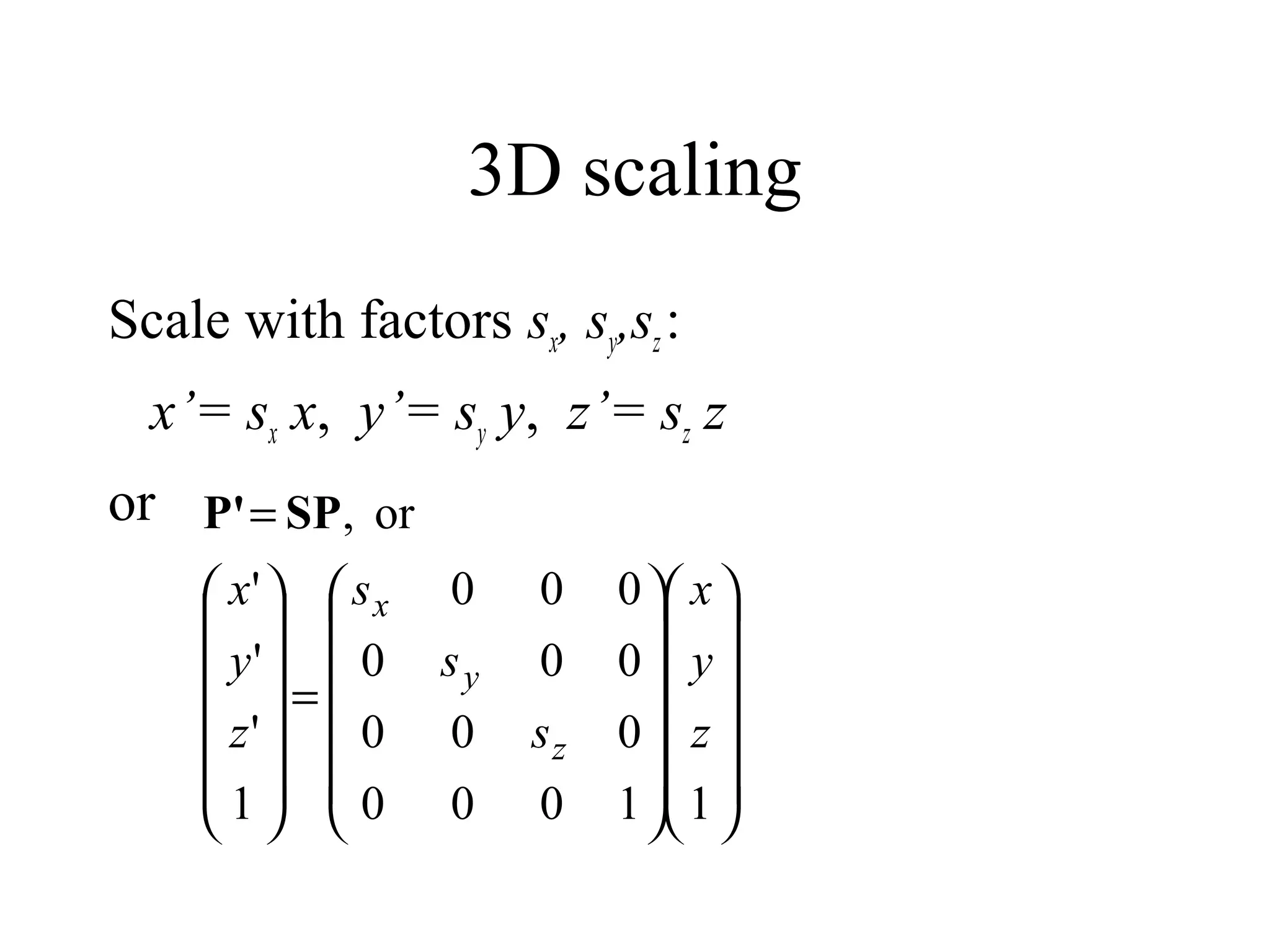
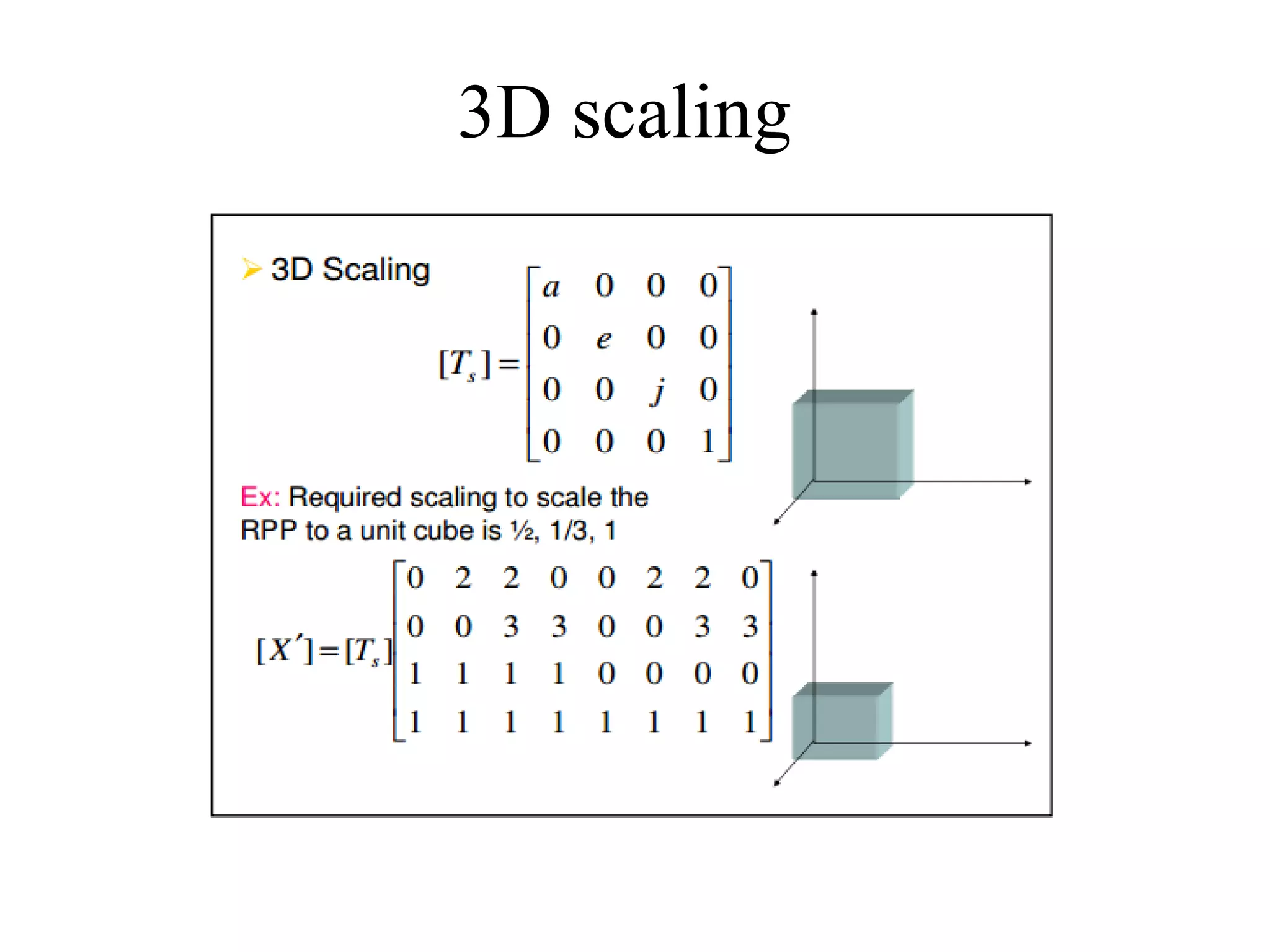
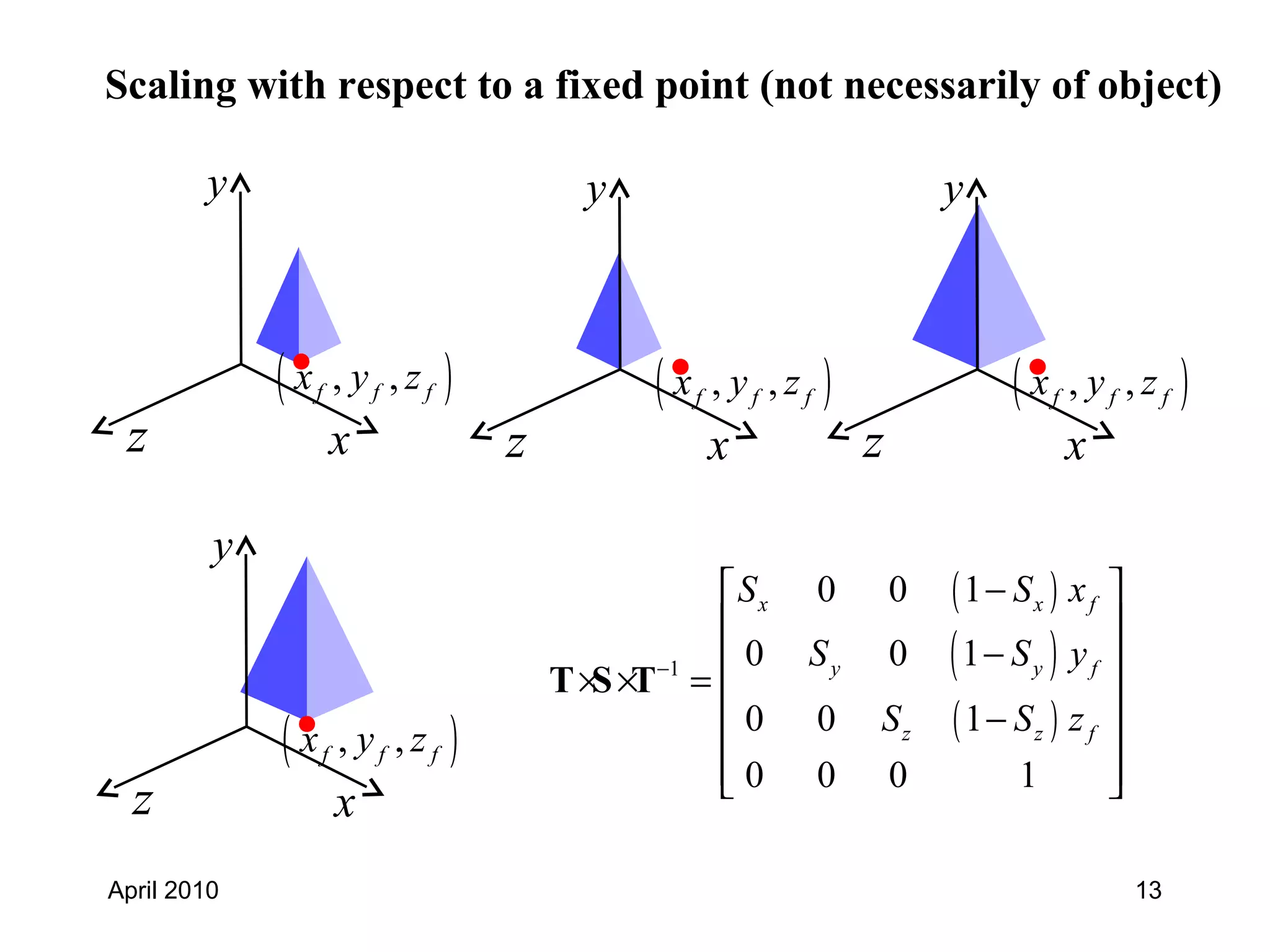
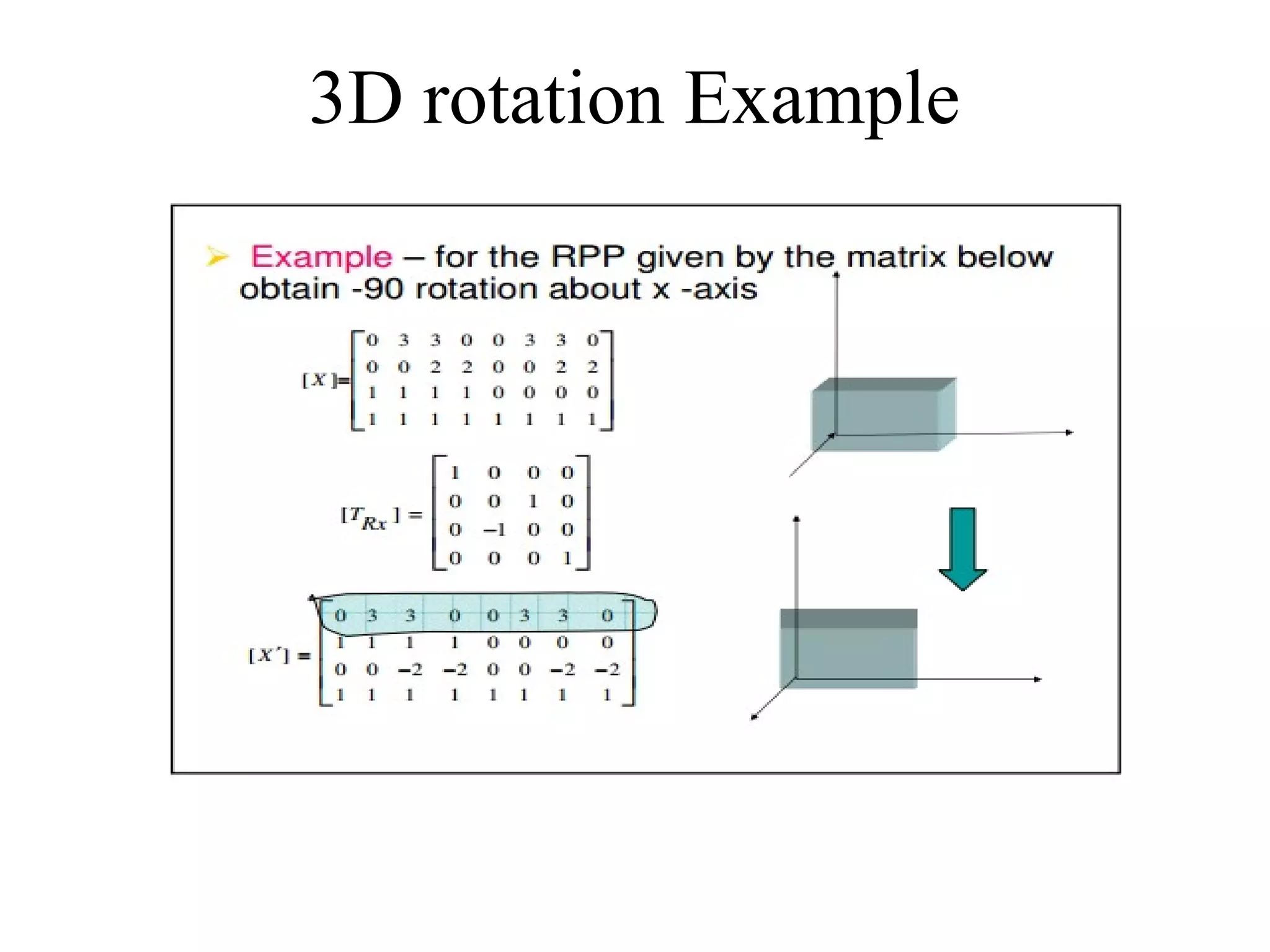
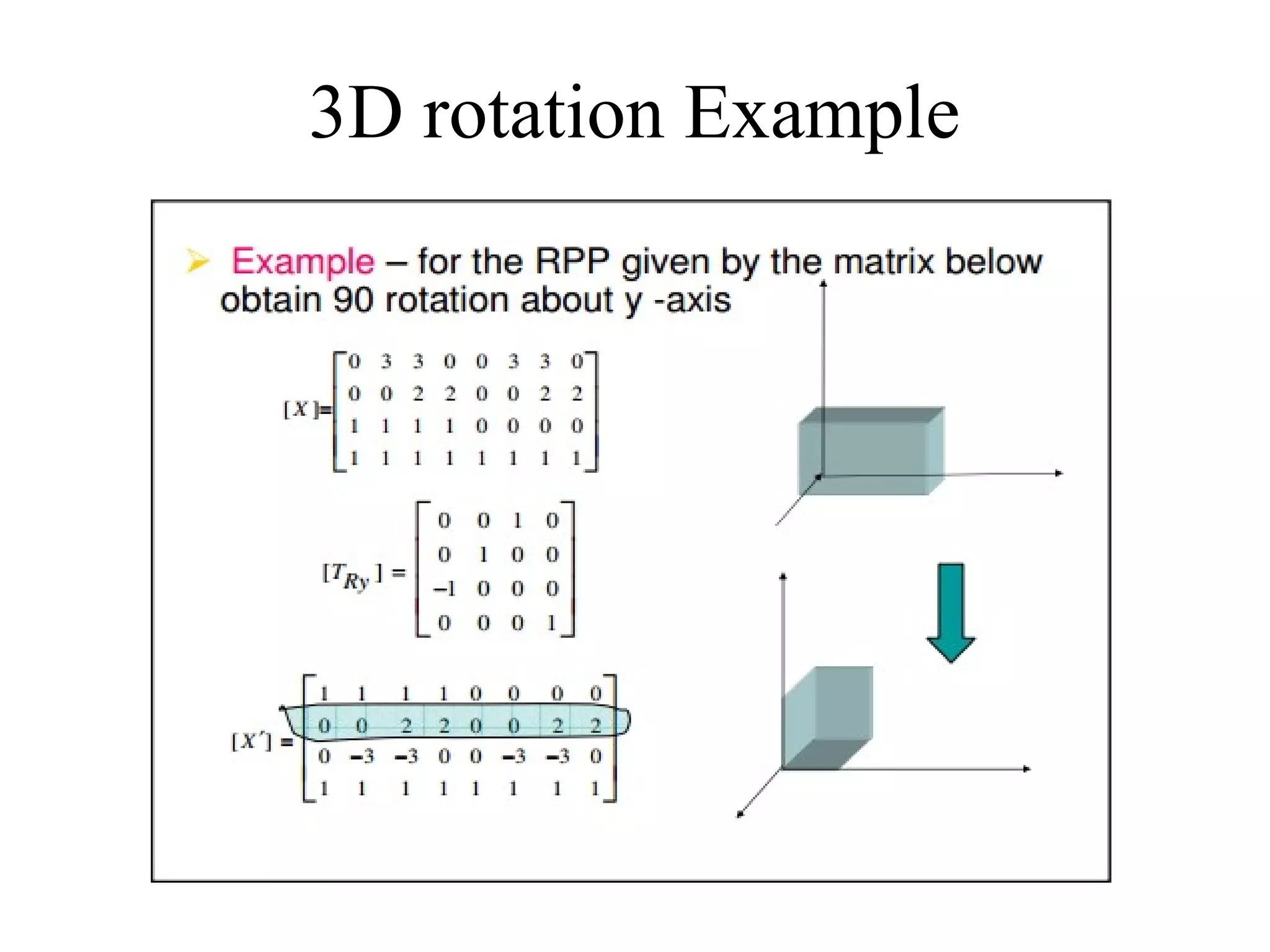
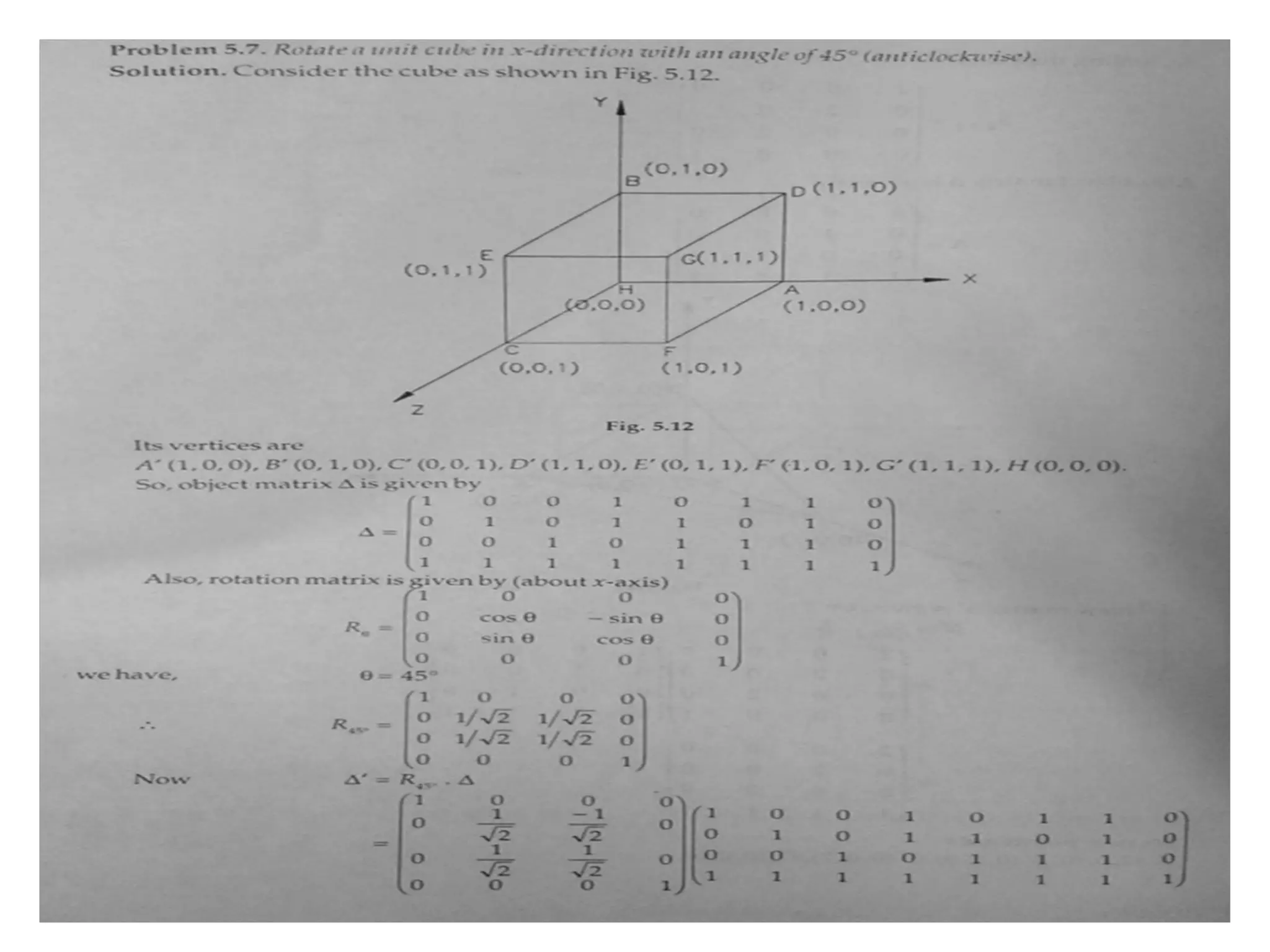
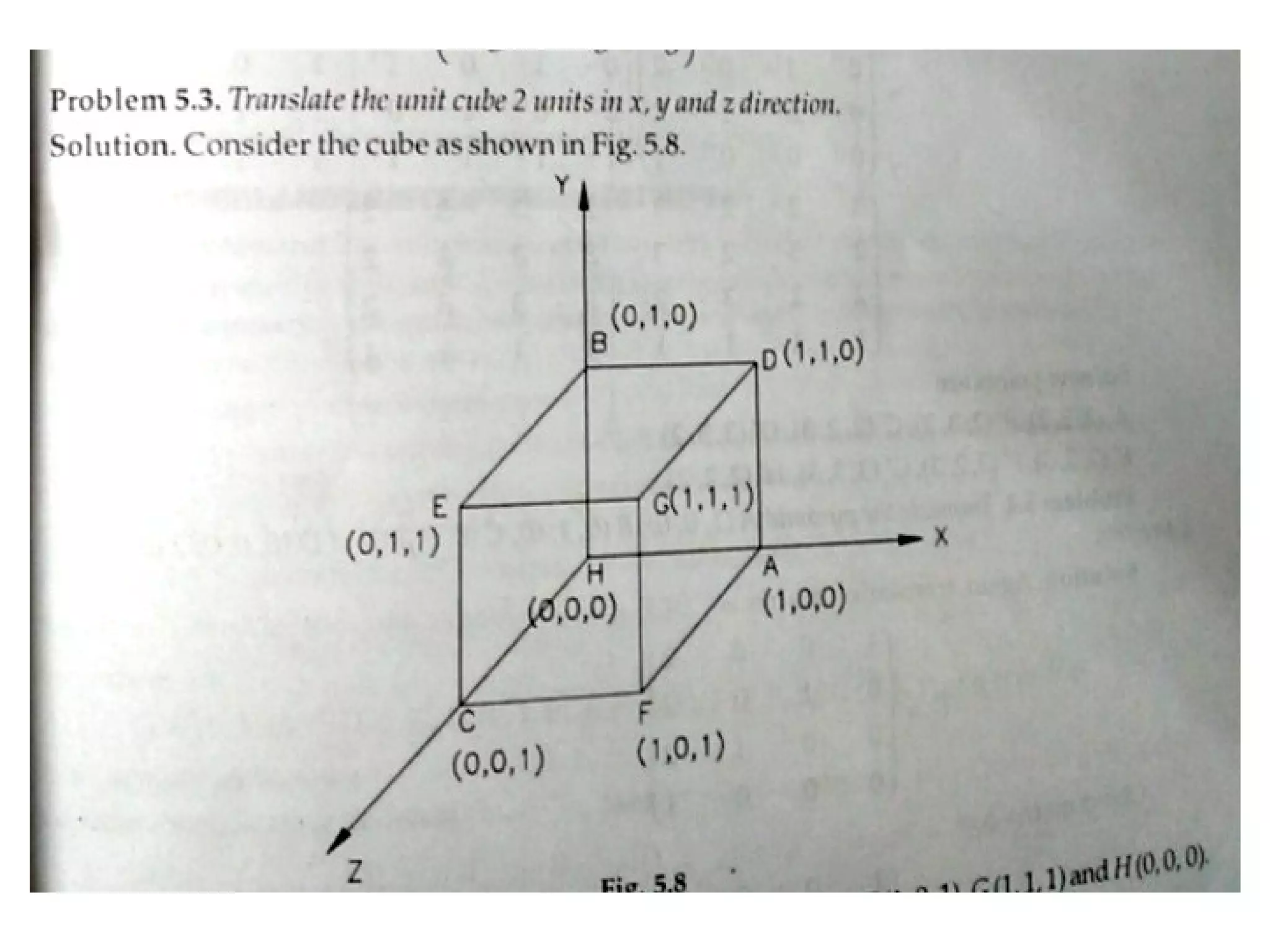
This document discusses 3D transformations in computer graphics including translation, rotation, scaling, and shearing. Translation simply moves an object along the x, y, and z axes and can be represented by a 4x4 matrix. Rotation is more complex in 3D and involves rotating around the x, y, or z axes. Scaling enlarges or shrinks an object along the x, y, and z axes. Shearing skews an object by changing the coordinates of one axis based on the values of another axis. The document provides formulas and examples for performing each type of 3D transformation.

1. Computer Graphics
3D Transformations
Total Slides 29

2. From 2D to 3D
• Translation is simple as in 2D
• Use of Homogeneous coordinate in 3D
– In 3D transformation always use Matrix: 4x4
• All transformation in 3D is simple but only
Rotation transformation is complex in 3D
transformation.

3. 3D Translation
Translate using (tx, ty,tz):
x’=x+ tx, y’=y+ ty , z’=z+ tz
or
x
y
P
P+T
T
z










=










=










=
+=
z
y
x
t
t
t
z
y
x
z
y
x
TPP
TPP'
en,
'
'
'
'
met,

4. 3D Translation 2
In 4D homogeneous coordinates:
x
y
P
P+T
T
z
11000
100
010
001
1
'
'
'
or,




























=














=
z
y
x
t
t
t
z
y
x
z
y
x
MPP'

5. 3D Rotation 1
z
P
x
y
P’
α
1000
0100
00cossin
00sincos
)(
with,)(
Or
'
cossin'
sincos'
:as-aroundangleoverRotate













 −
=
=
=
+=
−=
αα
αα
α
α
αα
αα
α
z
z
zz
yxy
yxx
z
R
PRP'

6. 2D Rotation about the origin.
y
x
r
r
P’(x’,y’)
P(x,y)
θ
φ
y
φ
φ
sin.
cos.
ry
rx
=
=
x
θφθφφθ
θφθφφθ
cos.sin.sin.cos.)sin(.
sin.sin.cos.cos.)cos(.
rrry
rrrx
+=+=′
−=+=′

8. 3D Rotation 2
z
x
y
Rotation around axis:
- Counterclockwise, viewed from rotation axis
z
x
y z
x
y

9. 3D Rotation 3
z
x
y
z
x
y z
x
y
zy
yx
xz
→
→
→
xz
zy
yx
→
→
→
Rotation around axes:
Cyclic permutation coordinate axes
xzyx →→→

10. 3D Rotation
zy
yx
xz
→
→
→
1000
0100
00cossin
00sincos
)(
with,)(
Or
'
cossin'
sincos'
:as-aroundangleoverRotate













 −
=
=
=
+=
−=
αα
αα
α
α
αα
αα
α
z
z
zz
yxy
yxx
z
R
PRP'
1000
0cossin0
0sincos0
0001
)(
with,)(
Or
'
cossin'
sincos'
:as-aroundangleoverRotate














−
=
=
=
+=
−=
αα
αα
α
α
αα
αα
α
x
x
xx
zyz
zyy
x
R
PRP'

11. 11000
000
000
000
1
'
'
'
or,




























=














=
z
y
x
s
s
s
z
y
x
z
y
x
SPP'
3D scaling
Scale with factors sx, sy,sz:
x’= sx x, y’= sy y, z’= sz z
or

12. 3D scaling

13. April 2010 13
( ), ,f f fx y z
x
y
z
Scaling with respect to a fixed point (not necessarily of object)
( ), ,f f fx y z
x
y
z
( ), ,f f fx y z
x
y
z
( ), ,f f fx y z
x
y
z
( )
( )
( )
1
0 0 1
0 0 1
0 0 1
0 0 0 1
x x f
y y f
z z f
S S x
S S y
S S z
−
− 
 
− × × =  
− 
  
T S T

14. 3D Shearing about X,Y,Z Axis
• Shearing about X axis- X coordinate will change but no
change in Y and Z axis coordinate.
• Shearing about Y axis- Y coordinate will change and
changes are made only in X and Z axis.
• Shearing about Z axis- Z coordinate will change but no
change in X and Y axis.
1 0 0 0
1 0 0
0 1 0
0 0 0 1
shy
shz
 
 
 
 
 
 
1 0 0
0 1 0 0
0 1 0
0 0 0 1
Shx
Shz
 
 
 
 
 
 
1 0 0
0 1 0
0 0 1 0
0 0 0 1
Shx
Shy
 
 
 
 
 
 

15. 3D rotation Example

16. 3D rotation Example

17. Combine 3D Transformation

18. 3D Combine Transformations

22. Question
• Translate a Pyramid whose coordinates are
(0,0,0), (1,0,0) (0,0,1) and (0,1,0). Translate
this pyramid 3 unit x, y, z direction and find
out final transformed matrix.
• Find the rotation matrix along x, y, z axis
using derivation of rotation in 2D.

23. Thank You!!