Embed presentation
Download to read offline










The document discusses 3D transformations, focusing on rotation, scaling, and shear transformations, each requiring specific parameters such as rotation axes, scaling factors, and shearing directions. It emphasizes the use of transformation matrices, typically 3x3 or 4x4, to manipulate object coordinates in 3D space. Various mathematical representations illustrate the effects of these transformations on object shapes.












Introduction to the concept of 3D transformation and its representation in matrix form.
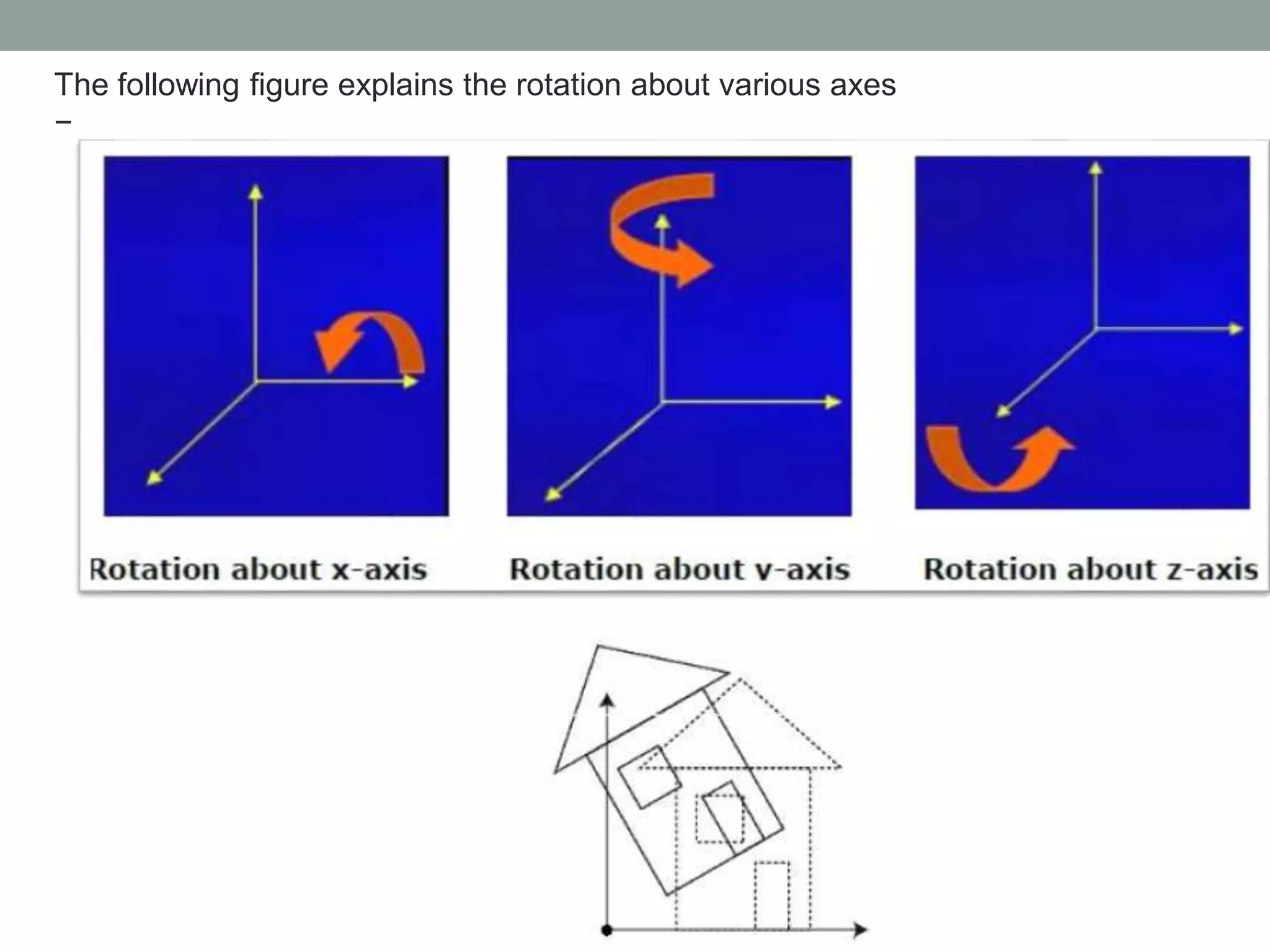
Explains 3D rotation, including the necessity of specifying angles and axes for X, Y, Z rotations.
Describes the scaling transformation in 3D, detailing the expansion or compression of objects using scaling factors.
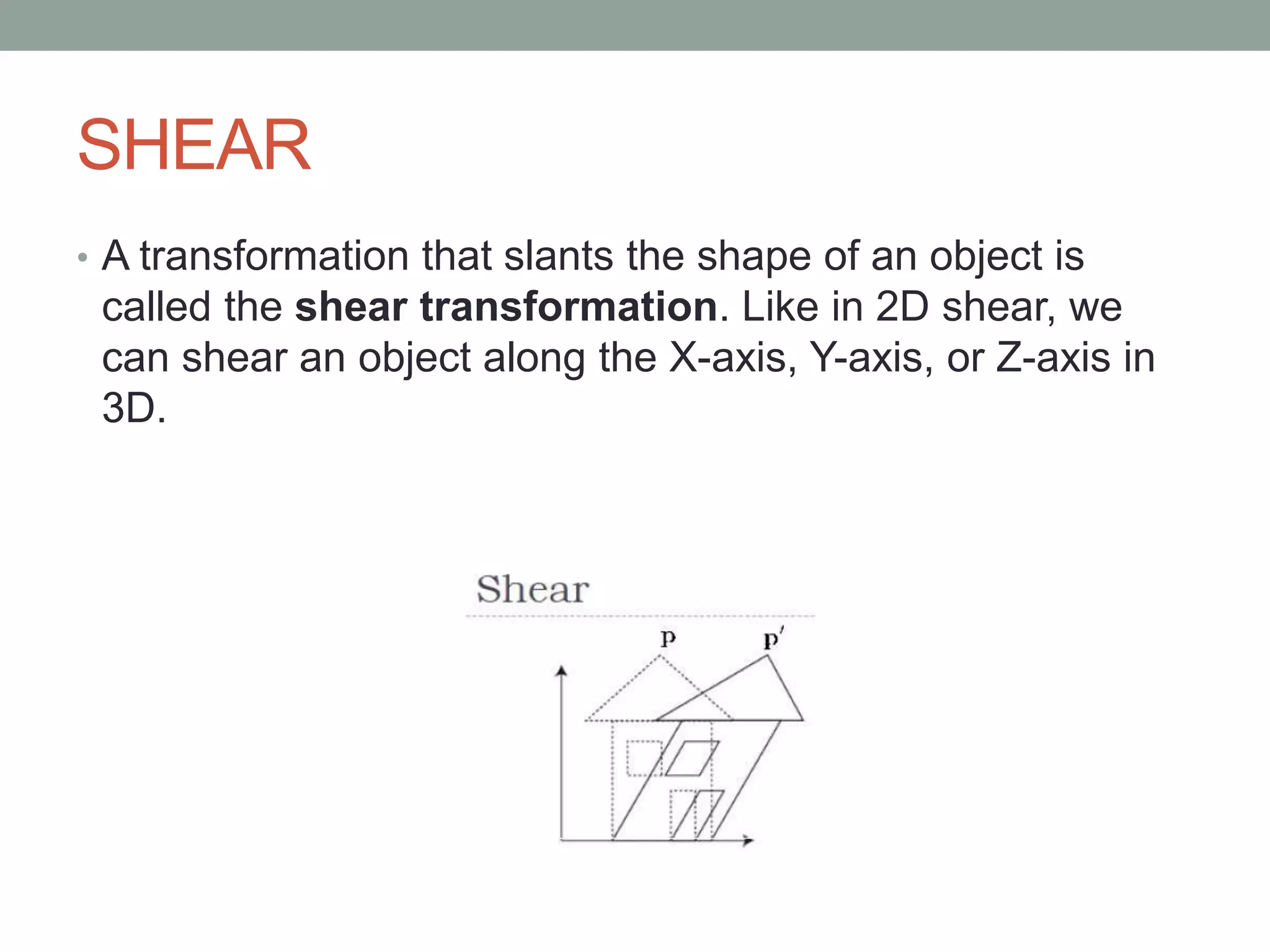
Defines shear transformation in 3D, highlighting the slanting of object shapes along X, Y, and Z axes.
Introduces transformation matrices as key tools in 3D operations, often using 3x3 or 4x4 matrix formats.