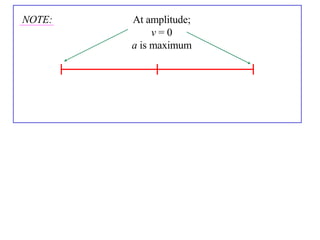
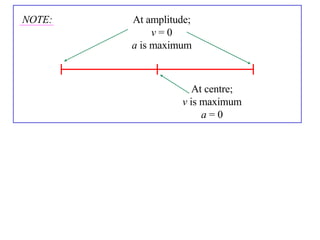
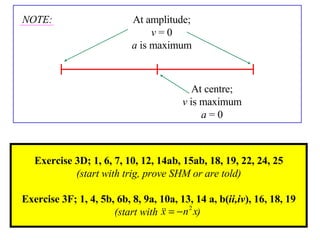
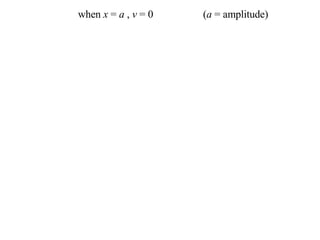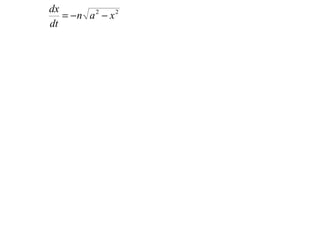The document discusses simple harmonic motion (SHM), where a particle moves back and forth such that its acceleration is directly proportional to its distance from a fixed point. SHM has the properties that the particle's velocity is zero at the amplitude of its oscillation, and it travels between the points of -a and +a on its axis. Examples are given of particles moving according to SHM equations, and exercises are provided to practice determining SHM, periods of motion, and maximum values.

1. Simple Harmonic Motion

2. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM)

3. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM)

4. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM)

5. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM)

6. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM) (constant needs to be negative)

7. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM) (constant needs to be negative)

8. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM) (constant needs to be negative)

9. Simple Harmonic Motion A particle that moves back and forward in such a way that its acceleration at any instant is directly proportional to its distance from a fixed point, is said to undergo Simple Harmonic Motion (SHM) (constant needs to be negative)

10. when x = a , v = 0 ( a = amplitude)

11. when x = a , v = 0 ( a = amplitude)

12. when x = a , v = 0 ( a = amplitude)

13. NOTE: when x = a , v = 0 ( a = amplitude)

14. NOTE: when x = a , v = 0 ( a = amplitude)

15. NOTE: when x = a , v = 0 ( a = amplitude)

16. NOTE: Particle travels back and forward between x = - a and x = a when x = a , v = 0 ( a = amplitude)

24. In general;

25. In general;

26. In general;

27. In general;

28. In general;

29. In general;

30. In general; the particle has;

31. In general; the particle has;

32. In general; the particle has; (time for one oscillation)

33. In general; the particle has; (time for one oscillation) (number of oscillations per time period)

34. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t .

35. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion.

36. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion.

37. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion.

38. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion.

39. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion.

40. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion.

41. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion. b) Find the interval in which the particle moves and determine the greatest speed.

42. e.g. ( i ) A particle, P, moves on the x axis according to the law x = 4sin3 t . a) Show that P is moving in SHM and state the period of motion. b) Find the interval in which the particle moves and determine the greatest speed.

43. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

44. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

45. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

46. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

47. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

48. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

49. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

50. ( ii ) A particle moves so that its acceleration is given by Initially the particle is 3cm to the right of O and traveling with a velocity of 6cm/s. Find the interval in which the particle moves and determine the greatest acceleration.

51. NOTE:

52. NOTE: At amplitude; v = 0 a is maximum

53. NOTE: At amplitude; v = 0 a is maximum At centre; v is maximum a = 0

54. Exercise 3D; 1, 6, 7, 10, 12, 14ab, 15ab, 18, 19, 22, 24, 25 (start with trig, prove SHM or are told) Exercise 3F; 1, 4, 5b, 6b, 8, 9a, 10a, 13, 14 a, b( ii,iv ), 16, 18, 19 (start with ) NOTE: At amplitude; v = 0 a is maximum At centre; v is maximum a = 0