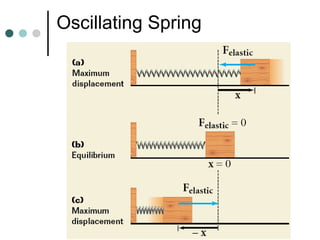
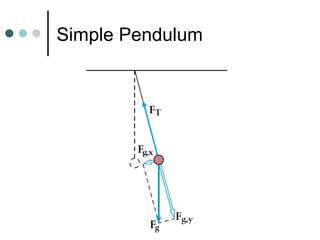
This document discusses simple harmonic motion and compares oscillating springs and pendulums. It defines simple harmonic motion as vibration about an equilibrium position where a restoring force is proportional to displacement. Springs and pendulums are given as examples that exhibit simple harmonic motion. The restoring force of a spring is described by Hooke's law as being proportional to displacement. For both springs and pendulums, the period of oscillation depends only on intrinsic properties and is independent of amplitude.

1. Simple Harmonic
Motion
Physics
1/23/2013

2. Simple Harmonic Motion
 simple harmonic motion (SHM) –
vibration about an equilibrium position
in which a restoring force is
proportional to the displacement from
equilibrium
 two common types of SHM are a
vibrating spring and an oscillating
pendulum
 springs can vibrate horizontally (on a
frictionless surface) or vertically

3. Oscillating Spring

4. SHM and Oscillating Springs
 in an oscillating spring, maximum
velocity (with Felastic = 0) is experienced
at the equilibrium point; as the spring
moves away from the equilibrium
point, the spring begins to exert a
force that causes the velocity to
decrease
 the force exerted is maximum when
the spring is at maximum
displacement (either compressed or
stretched)

5. SHM and Oscillating Springs
 at maximum displacement, the
velocity is zero; since the spring is
either stretched or compressed at this
point, a force is again exerted to start
the motion over again
 in an ideal system, the mass-spring
system would oscillate indefinitely

6. SHM and Oscillating Springs
 damping occurs when friction slows
the motion of the vibrating mass,
which causes the system to come to
rest after a period of time
 if we observe a mass-spring system
over a short period of time, damping is
minimal and we can assume an ideal
mass-spring system

7. SHM and Oscillating Springs
 in a mass-spring system, the spring
force is always trying to pull or push
the mass back toward equilibrium;
because of this, we call this force a
restoring force
 in SHM, the restoring force is
proportional to the mass’
displacement; this results in all SHM
to be a simple back-and-forth motion
over the same path

8. Hooke’s Law
 in 1678, Robert Hooke proposed this
simple relationship between force and
displacement; Hooke’s Law is
described as:
Felastic = -kx
 where Felastic is the spring force,
 k is the spring constant
 x is the maximum displacement from
equilibrium

9. Hooke’s Law
 the negative sign shows us that the force is
a restoring force, always moving the object
back to its equilibrium position
 the spring constant has units of
Newtons/meter
 the spring constant tells us how resistant a
spring is to being compressed or stretched
(how many Newtons of force are required to
stretch or compress the spring 1 meter)
 when stretched or compressed, a spring
has potential energy

10. Simple Pendulum
 simple pendulum – consists of a mass
(called a bob) that is attached to a
fixed string; we assume that the mass
of the bob is concentrated at a point at
the center of mass of the bob and the
mass of the string is negligible; we
also disregard friction and air
resistance

11. Simple Pendulum

12. Simple Pendulum
 for small amplitude angles (less than
15°), a pendulum exhibits SHM
 at maximum displacement from
equilibrium, a pendulum bob has
maximum potential energy; at
equilibrium, this PE has been
converted to KE
 amplitude – the displacement from
equilibrium

13. Period and Frequency
 period (T) – the time, in seconds, to
execute one complete cycle of motion;
units are seconds per 1 cycle
 frequency (f) – the number of
complete cycles of motion that occur
in one second; units are cycles per 1
second (also called hertz)

14. Period and Frequency
 frequency is the reciprocal of period, so
 the period of a simple pendulum depends
on the length of the string and the value for
free-fall acceleration (in most cases, gravity)

15. Period of a Simple
Pendulum
 notice that only length of the string and the
value for free-fall acceleration affect the
period of the pendulum; period is
independent of the mass of the bob or the
amplitude

16. Period of a Mass-Spring
System
 period of a mass-spring system depends on
mass and the spring constant
 notice that only the mass and the spring
constant affect the period of a spring; period
is independent of amplitude (only for
springs that obey Hooke’s Law)

17. Comparison of a Pendulum
and an Oscillating Spring