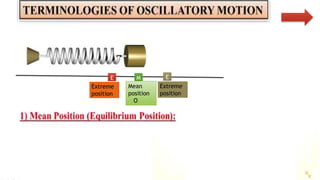
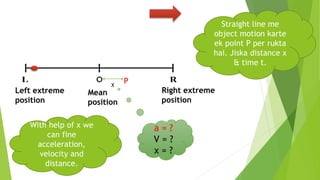
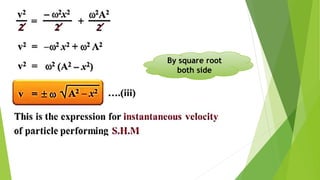
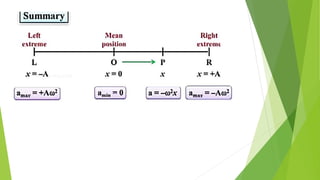
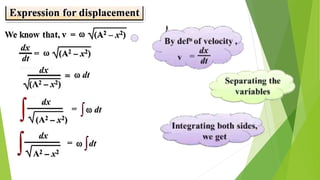
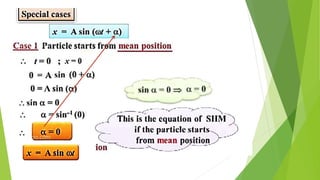
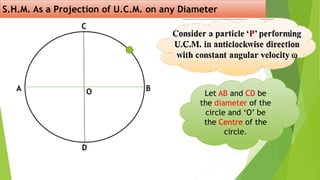
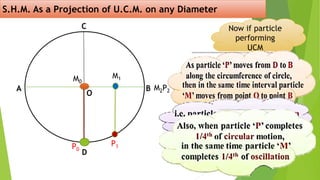
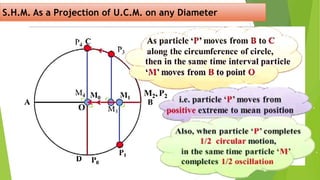
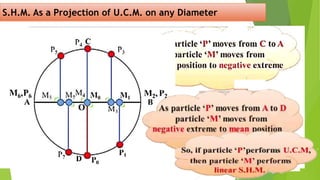
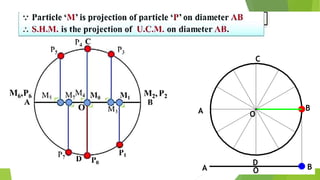
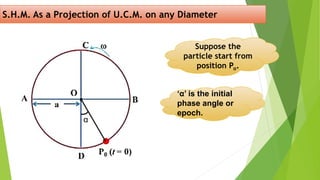
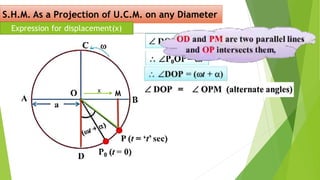
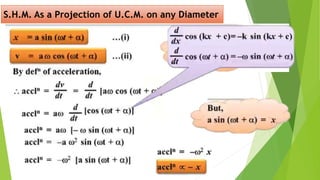
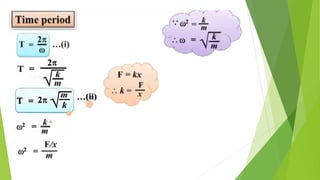
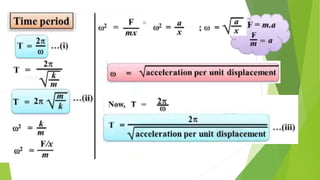
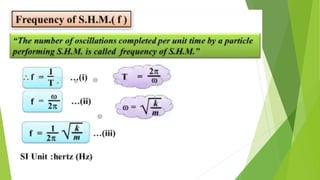
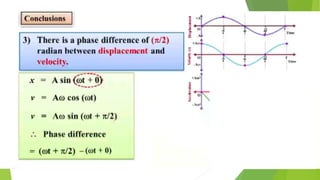
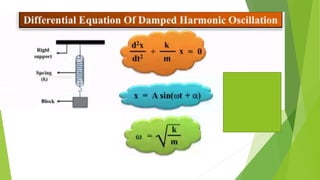
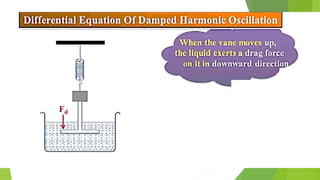
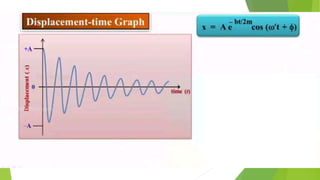
The document discusses concepts related to oscillatory motion, including oscillation types, harmonic motion, and simple harmonic motion (SHM). It covers the mechanics of linear and angular SHM, the relationship between displacement, velocity, and acceleration, and provides different equations and graphical representations to illustrate these concepts. Additionally, it introduces the simple pendulum, its motion, and relevant laws governing pendulum behavior.

1. Oscillation

7. Tuning
fork
Spring of
mass

8. Are oscillatory
motion is
periodic
motion?

10. Terminologies of Oscillatory
motion

11. E M E
Extreme
position
Mean
position
O
Extreme
position

13. Extreme
position
Mean
position
O
Extreme
position
E M E
Extreme
position
Mean
position
O
Extreme
position

14. AGAR ISE CARTESIAN SE
UNDERSTAND KARE TO EK
EXTREME POINT + AND –VE.
- +
P called left
extreme or –ve
extreme.
R called right
exteme or + ve
extreme.
R

15. Isme bhi 2 Type
displacement hoga
particle agar left side ka
distanct cover karega to
–ve displacement and
RHD + displacement.

16. Mean position se
extreme position
ke distance ko
amplidtude kehte
hai.
Isme bhi 2 type.
A+ and A-

17. Ek extreme se
dusre extreme ka
distance range or
path length hai.

18. One osclllation = mean positin se start and
cover right extreme then left exteme then
again come mean position.

20. Harmonic motion

21. Harmonic motion

22. Koi bhi spring jab
movement karta hai to
oske displacement,
velocitiy and
acceleration me time ke
based continuous
changes ata hai jise
graph se show kiya hai.
Jise meths ke zarie
show karte hai.

23. Simple Harmonic Motion

24. SHM me 2 type hai linear
and angular.
Linear means straight
motion and angular mean
making angle motion.

25. Linear simple Harmonic motion

26. F

29. Now remaining concept is
same because again
distance and force are in
opposite directin so same
forumula
F = -kx

32. Definition of linear SHM

34. F= restoring force.

35. Aise motion linear
nahi hosakte kynki
inka distance depend
hota rehta hai gravity
ki waha se.

36. Differential Equation of the linear S.H.M

37. F = ma
But Acc. to
newton second
law Force
formula is
F=ma.
But Acceleration is a = dv/dt
Velocity is v = dx/dt
Now put v ka value
in acceleration
forumula dv me.

38. Substituting equation (iii) in equation
(i)
Divide
by m

40. Expression for Acceleration
in linear S.H.M

41. Left extreme
position
Right extreme
position
Mean
position
PX
a = ?
V = ?
x = ?
Straight line me
object motion karte
ek point P per rukta
hai. Jiska distance x
& time t.
With help of x we
can fine
acceleration,
velocity and
distance.

42. We already found
a = d2x/dt2
- Sign indicate
acceleration and
displacement are in
opposite direction.
We know angular
velocity is const.
then…

43. Kya ho agar particle
mean position pe ho.
To displacement zero
hoga.

45. Expression for Velocity in
Linear S.H.M

46. Multiply and divide by dx
Separating the
variable

47. Where ‘c’ constant of integration.

50. By square root
both side

51. Expression for Maximum
and Minimum velocity
Expression for Displacement
in Linear S.H.M

57. Taking sin both
side,

60. S.H.M. As a Projection of U.C.M.
on any Diameter
S.H.M.

61. S.H.M. As a Projection of U.C.M. on any Diameter
A O B
C
D
Let AB and CD be
the diameter of the
circle and ‘O’ be
the Centre of the
circle.

62. S.H.M. As a Projection of U.C.M. on any Diameter
A
O
B
C
D
At time t=0,
the particle P0
is at point D
P0
From ‘P0’ draw
a perpendicular
on diameter AB
M0

63. S.H.M. As a Projection of U.C.M. on any Diameter
A
O
B
C
D
P0
M0
Now if particle
performing
UCM
P1
M1
M2P2

64. S.H.M. As a Projection of U.C.M. on any Diameter

65. S.H.M. As a Projection of U.C.M. on any Diameter

66. A O
B
C
D
A O B

67. A O
B
C
D
A O B

68. Derivation of S.H.M as a projection
of U.C.M on any diameter

69. S.H.M. As a Projection of U.C.M. on any Diameter
A O B
C
D
Consider, a particle
performing U.C.M
with an angular
velocity ω along a
circle of radius ‘a’.
a
ω

70. S.H.M. As a Projection of U.C.M. on any Diameter
Suppose the
particle start from
position Po.
α
‘α’ is the initial
phase angle or
epoch.

71. Let, in time ‘t’ the
particle reaches
point P
θ = ?
S.H.M. As a Projection of U.C.M. on any Diameter

72. S.H.M. As a Projection of U.C.M. on any Diameter
M
Expression for displacement(x)
x

73. S.H.M. As a Projection of U.C.M. on any Diameter
M
Expression for displacement(x)
x

74. S.H.M. As a Projection of U.C.M. on any Diameter
M
Expression for displacement(x)
x

75. S.H.M. As a Projection of U.C.M. on any Diameter
a = constant

76. S.H.M. As a Projection of U.C.M. on any Diameter

77. M

78. Phase of S.H.M 1

80. Magnitude matlab angle
, distance, a, v ka
measure asani se
karsakte hai. Aur saath
saath direction pata
karsakte hai motion
kidhar horaha hai.

81. Agar mujhe angle pata ho to me
easily x ki value find kar sakta
hoo.

82. If angle is 0 degree
iska matlab
displacement
particle mean
postion se start ho
rahe hai.

83. OB wala particle zero se start
hua hai. Isliye angle 0. and DB
wala object distance cover
karke 90 degree angle bana
raha hai.

84. Magnitude means
oscillation ki state
bataye mean a,v,t,x
etc.

85. INITIAL PHASE (EPOCH) OF S.H.M.

87. YEH wo phase hai jaha per
particle apni initial stage per
hai abhi movement start nahi
ki isliye angle 0 means mean
postion.

90. Expression fro time period and
frequency in linear S.H.M

91. x

92. Hamara
particle R
side hai.

96. Graphical Representation of
S.H.M- Mean position-1

102. A
0
0 -A 0

105. 0

115. Introduction to Simple pendulum

116. Simple pedulam me ek
heavy mass jise bob kehte
hai. String jisse bob tigh
kiya hai.
Pendulam ki length bob se
rigid ka distance hai.

118. Motion of Simple Pendulam as
S.H.M.

119. If pendulum is
displaced through a
angle θ

120. Motion of Simple Pendulum as a S.H.M.
mg

121. x

128. Expression for time period
Laws of simple pendulum
Second pendulum

133. If π =constant.

134. Damped Force

135. NO
Why?

140. Differential equation of Damped
Harmonic Oscillations

150. Displacement equation of dumped
harmonic oscillation