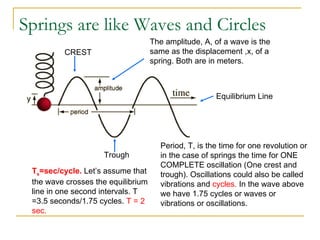
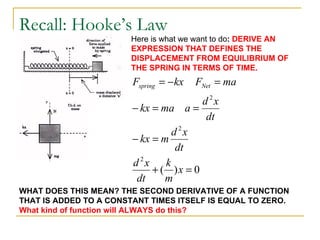
1) A spring with a spring constant of 110 N/m is displaced 1.5 m and released. 2) The system has a frequency of 0.75 Hz and a period of 1.34 seconds. 3) When released, the maximum velocity of the 5 kg mass is 7.05 m/s reached at the equilibrium position.

1. Harmonic Motion
AP Physics C

2. Springs are like Waves and Circles
The amplitude, A, of a wave is the
CREST same as the displacement ,x, of a
spring. Both are in meters.
Equilibrium Line
Period, T, is the time for one revolution or
Trough in the case of springs the time for ONE
COMPLETE oscillation (One crest and
Ts=sec/cycle. Let’s assume that trough). Oscillations could also be called
the wave crosses the equilibrium vibrations and cycles. In the wave above
line in one second intervals. T we have 1.75 cycles or waves or
=3.5 seconds/1.75 cycles. T = 2 vibrations or oscillations.
sec.

3. Frequency
The FREQUENCY of a wave is the inverse of the
PERIOD. That means that the frequency is the
#cycles per sec. The commonly used unit is
HERTZ(HZ).
seconds 3.5s
Period = T = = = 2s
cycles 1.75cyc
cycles 1.75cyc
Frequency = f = = = 0.5 c = 0.5 Hz
seconds 3.5 sec s
1 1
T= f =
f T

4. Recall: Hooke’s Law
Here is what we want to do: DERIVE AN
EXPRESSION THAT DEFINES THE
DISPLACEMENT FROM EQUILIBRIUM OF
THE SPRING IN TERMS OF TIME.
Fspring = −kx FNet = ma
d 2x
− kx = ma a =
dt
d 2x
− kx = m
dt
d 2x k
+ ( )x = 0
dt m
WHAT DOES THIS MEAN? THE SECOND DERIVATIVE OF A FUNCTION
THAT IS ADDED TO A CONSTANT TIMES ITSELF IS EQUAL TO ZERO.
What kind of function will ALWAYS do this?

5. A SINE FUNCTION!

6. Putting it all together: The bottom line
Since all springs exhibit properties of circle
motion we can use these expressions to
derive the formula for the period of a
spring.

7. The simple pendulum
Fr sin θ = τ = Iα
− mg sin θ ( L) = (mL2 )α
− g sin θ = Lα ifθ <<<, sin θ = θ
g
α + ( )θ = 0 If the angle is small,
L
mgcosθ
the “radian” value for
θ g 2π theta and the sine of
ω= , ω=
L T the theta in degrees
mg will be equal.
l
mgsinθ Tpendulum = 2π
g
A simple pendulum is one where a
mass is located at the end of string.
Once again, using our sine function
The string’s length represents the
model we can derive using circular
radius of a circle and has negligible
motion equations the formula for the
mass.
period of a pendulum.

8. The Physical Pendulum
A physical pendulum is an oscillating body that
rotates according to the location of its center of
mass rather than a simple pendulum where all the
mass is located at the end of a light string.
Fr sin θ = τ = Iα
− mg sin θd = Iα , d = L
2
− mgd = Iα ifθ <<<, sin θ = θ
mgd
α +( )θ = 0
I
It is important to understand
that “d” is the lever arm mgd 2π
ω= , ω=
distance or the distance from I T
the COM position to the point of I
rotation. It is also the same “d” in Tphysical pendulum = 2π
mgd
the Parallel Axes theorem.

9. Example
A spring is hanging from the ceiling. You know that if you
elongate the spring by 3.0 meters, it will take 330 N of force
to hold it at that position: The spring is then hung and a
5.0-kg mass is attached. The system is allowed to reach
equilibrium; then displaced an additional 1.5 meters and
released. Calculate the:
Spring Constant Fs = kx 330 = (k )(3)
k= 110 N/m
k k 110
Angular frequency
ω =
2
ω= = = 4.7 rad/s
m m 5

10. Example
A spring is hanging from the ceiling. You know that if you
elongate the spring by 3.0 meters, it will take 330 N of
force to hold it at that position: The spring is then hung
and a 5.0-kg mass is attached. The system is allowed to
reach equilibrium; then displaced an additional 1.5
meters and released. Calculate the:
Amplitude Stated in the question as 1.5 m
2π
ω = 2πf =
T
Frequency and Period ω 4.7
f = = = 0.75 Hz
2π 2π
2π 2π
T= = = 1.34 s
ω 4.7

11. Example
A spring is hanging from the ceiling. You know that if you
elongate the spring by 3.0 meters, it will take 330 N of
force to hold it at that position: The spring is then hung
and a 5.0-kg mass is attached. The system is allowed to
reach equilibrium; then displaced an additional 1.5
meters and released. Calculate the:
U s = 1 kx 2 = 1 kA2
Total Energy 2 2
U = 1 (110)(1.5) 2 = 123.75 J
2
Maximum velocity v = Aω = (1.5)(4.7) = 7.05 m/s

12. Example
A spring is hanging from the ceiling. You know that if you
elongate the spring by 3.0 meters, it will take 330 N of
force to hold it at that position: The spring is then hung
and a 5.0-kg mass is attached. The system is allowed to
reach equilibrium; then displaced an additional 1.5
meters and released. Calculate the:
Position of mass at maximum velocity At the equilibrium position
Maximum acceleration of the mass
a = ω 2 A = (4.7) 2 (1.5) = 33.135 m/s/s
Position of mass at maximum acceleration
At maximum amplitude, 1.5 m