An introduction to the basics of Simple Harmonic Motion, designed for NCEA level 3 students.

1. Introduction Key features Applications Simple Harmonic Motion

2. Simple Harmonic Motion is a type of periodic or oscillatory motion The object moves back and forth over the same path, like a mass on a spring or a pendulum We’re interested in it because we can use it to generalise about and predict the behaviour of a variety of repetitive motions What is SHM?

3. Period is the time taken for the motion to repeat one cycle Frequency is the number of cycles in a second Example: a cork bobbing on water is observed to move up and down twelve times in one minute. Find the frequency and the period T = 60/12 = 5.7s f = 1/T = 1/5.7 = 0.18Hz Definitions and vocabulary – 1

4. An important concept in SHM is equilibrium – this is the point in the middle of the motion Amplitude is the maximum displacement from the equilibrium Definitions and vocabulary - 2 Equilibrium position Amplitude – pendulum at maximum displacement

5. In SHM, we consider displacement, velocity, acceleration, force and energy Definitions and vocabulary - 3

6. The key to SHM (compared to other kinds of repetitive motion) is the way that force and acceleration change during each cycle Consider these two situations. Each one shows displacement from the equilibrium. In what direction will they move when released? How do I know something is SHM?

7. The mass on the spring and the pendulum will both move back towards the equilibrium when released Considering forces shows us that there will be a force acting towards the equilibrium Restoring force

8. Restoring force for a pendulum The weight force and the tension force are not equal and opposite If we resolve the forces we see that there is an inward-acting unbalanced force. This is the restoring force, and it causes an inward acceleration

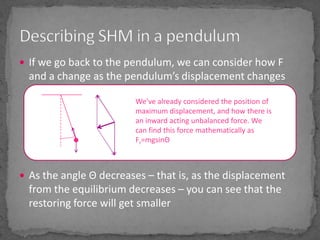
9. For motion to be Simple Harmonic Motion: there must be a restoring force acting towards the equilibrium the force is larger when the displacement is larger, and is a maximum at maximum displacement the force is zero at the equilibrium position Restoring force

10. We can also state the conditions for SHM using acceleration For motion to be Simple Harmonic Motion: The acceleration is directly proportional to the displacement from the equilibrium position The acceleration is always directed towards the equilibrium position Acceleration

11. We can express the acceleration mathematically a = - c y Where c is a positive constant. The value of c depends on the situation being considered Acceleration

12. If we go back to the pendulum, we can consider how F and a change as the pendulum’s displacement changes As the angle Θ decreases – that is, as the displacement from the equilibrium decreases – you can see that the restoring force will get smaller Describing SHM in a pendulum We’ve already considered the position of maximum displacement, and how there is an inward acting unbalanced force. We can find this force mathematically as Fr=mgsinΘ

13. Since we know that the restoring force is unbalanced, we know, via Newton’s First Law, that there will be acceleration. If the force gets smaller as the displacement gets closer to equilibrium, the acceleration must get smaller too At equilibrium, the weight force and the tension force are balanced, so the restoring force is zero and so, therefore, is the acceleration Describing SHM in a pendulum