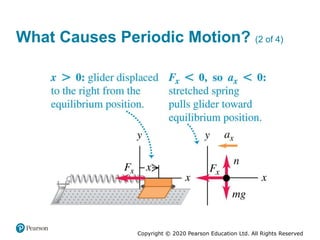
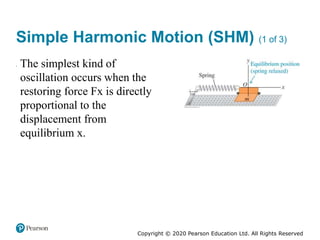
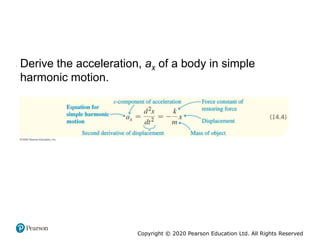
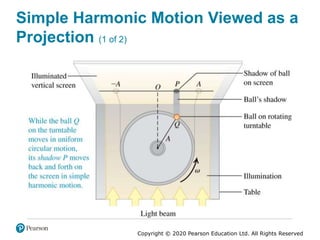
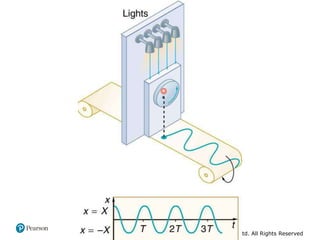
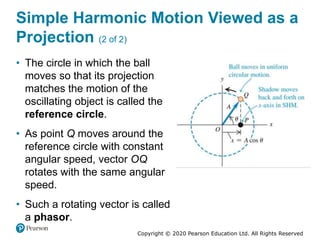
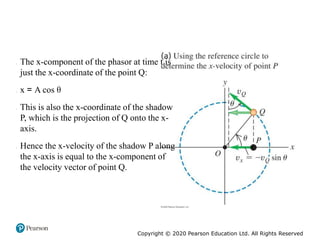
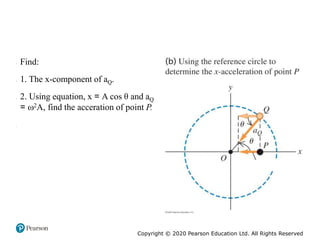
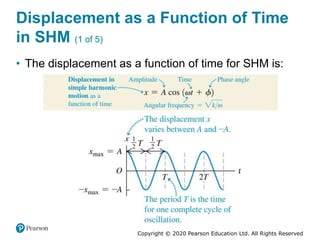
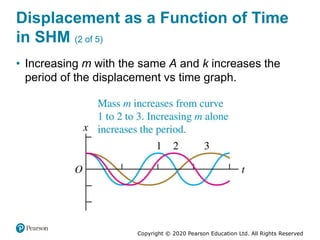
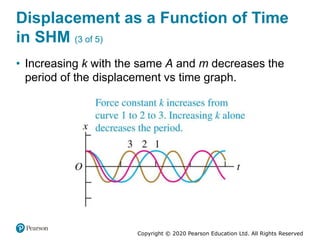
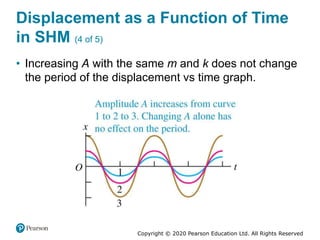
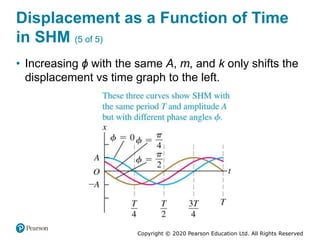
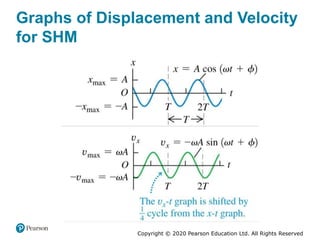
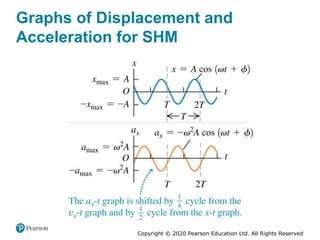
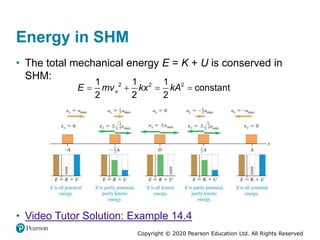
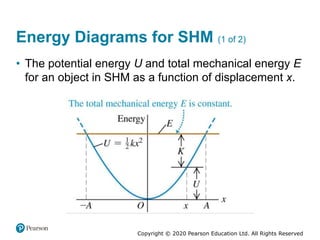
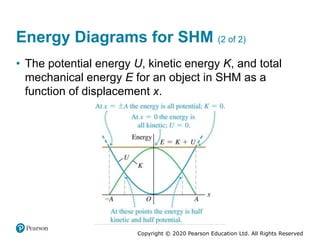
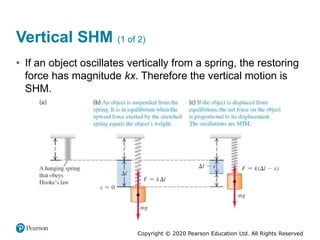
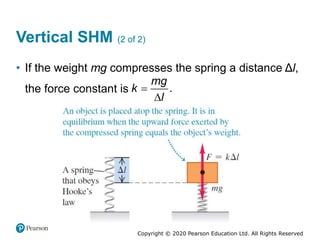
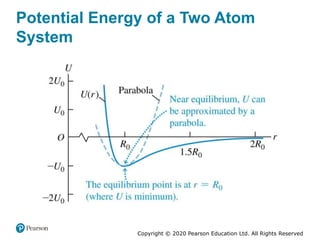
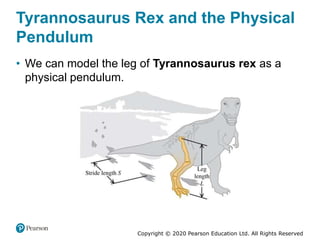
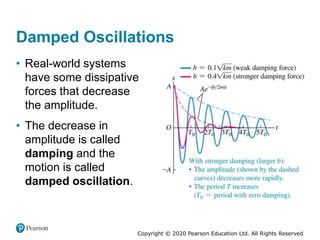
This document provides an overview of periodic motion and oscillations. It discusses key characteristics like amplitude, period, frequency, and angular frequency. Specific topics covered include simple harmonic motion, the behavior of springs, pendulums, molecular vibrations, damped oscillations, and forced oscillations. Examples are provided to illustrate concepts like calculating angular frequency from oscillation rate. The document also explores energy transfers and diagrams in oscillating systems.