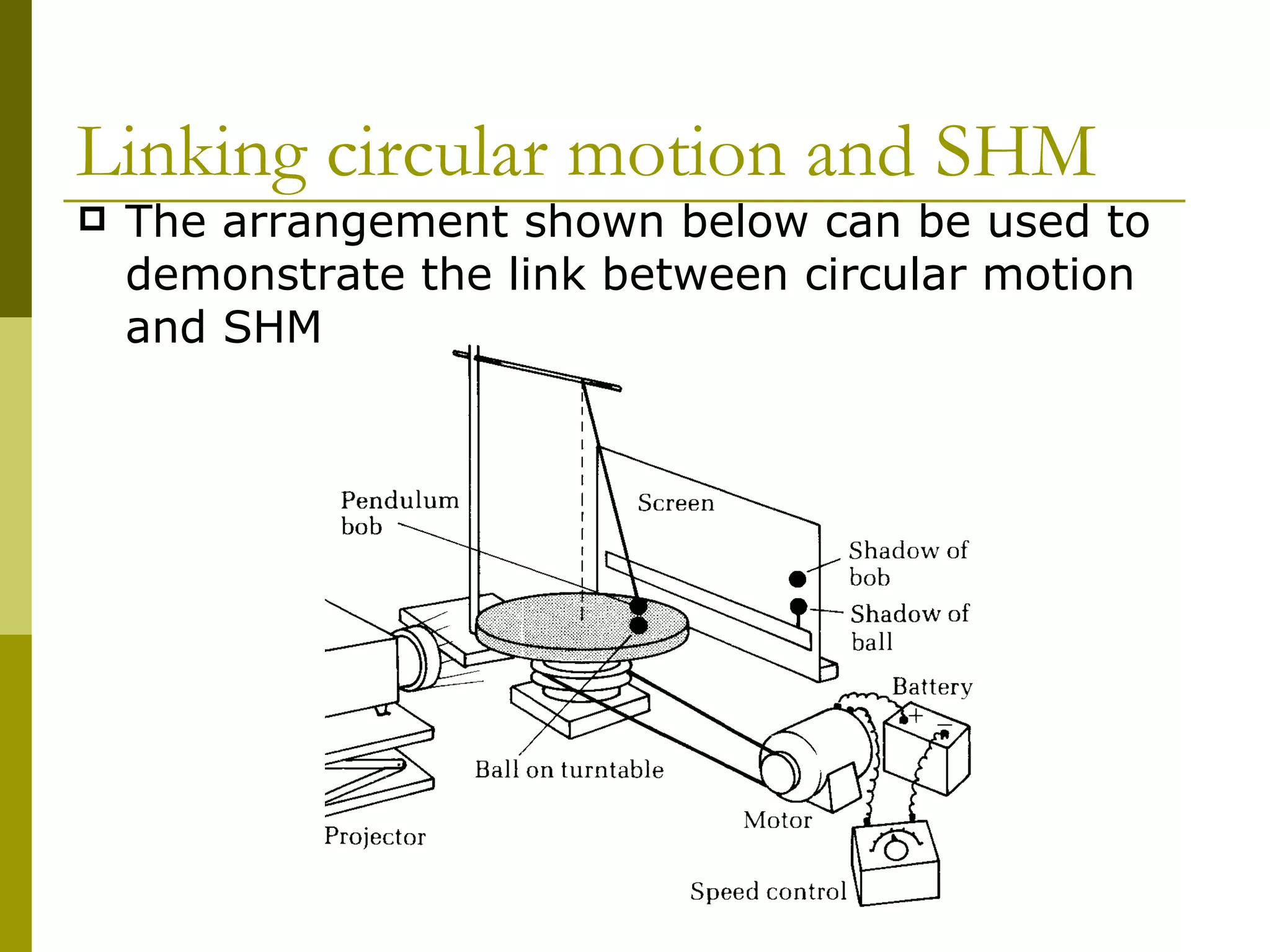
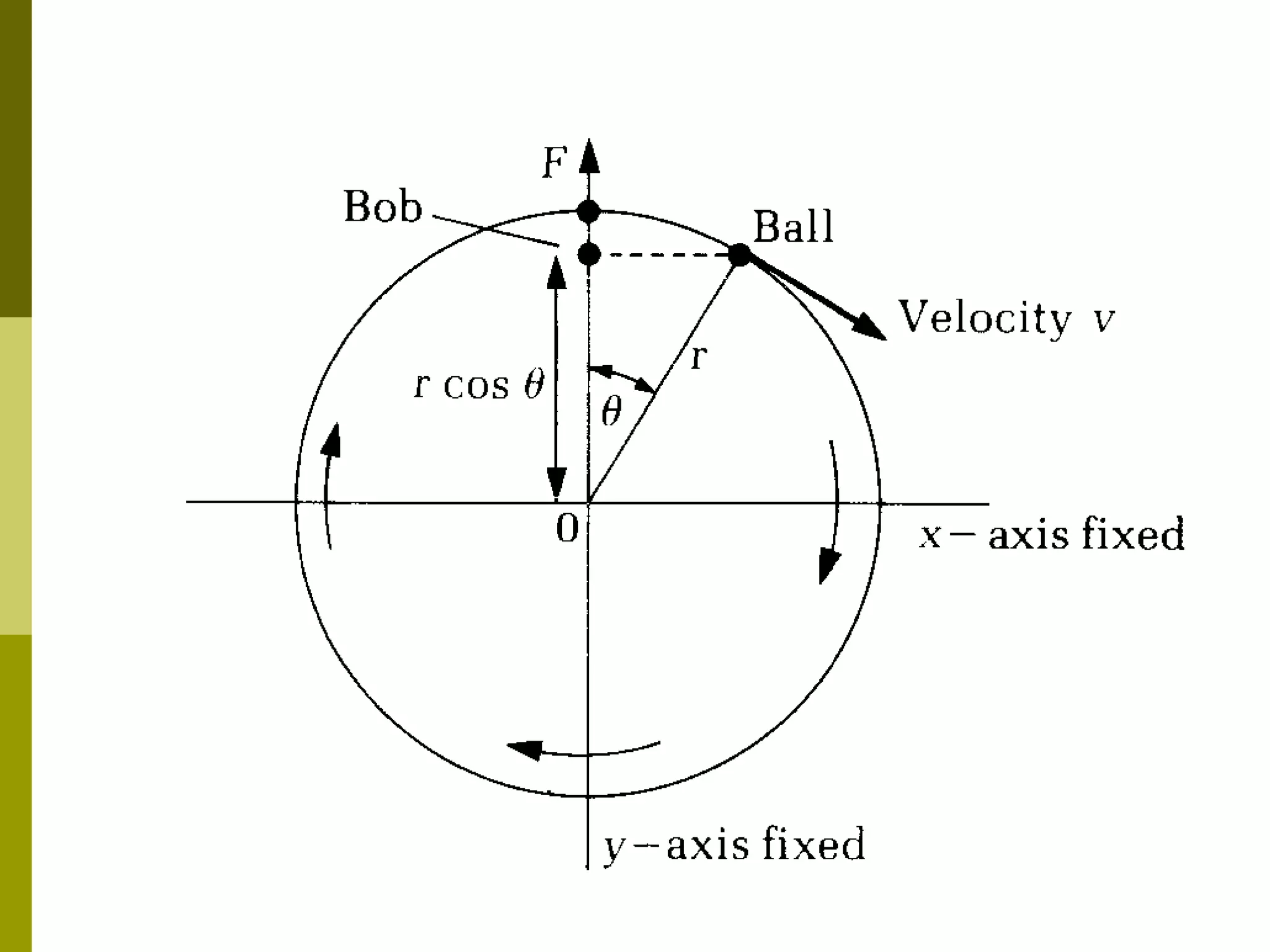
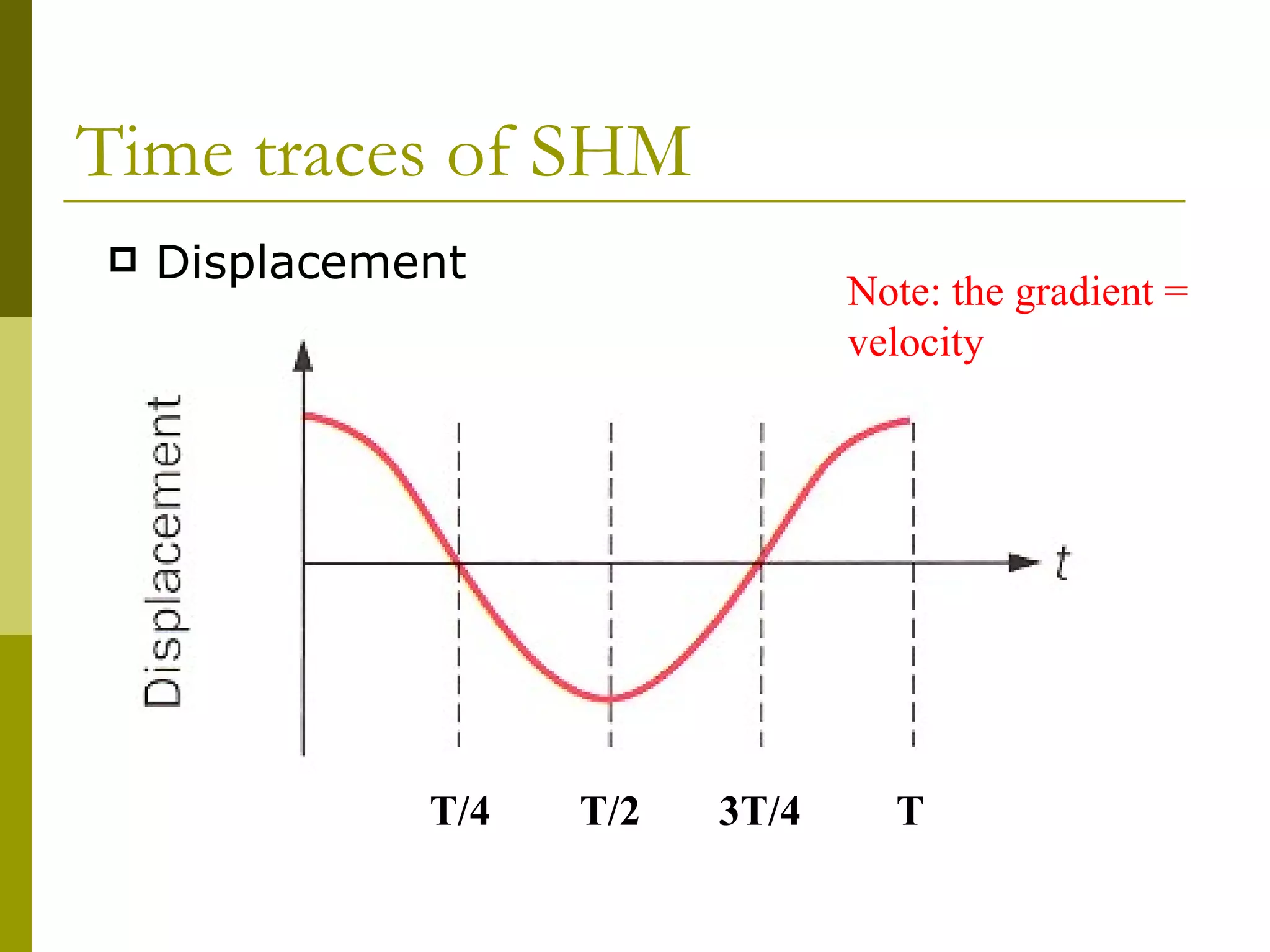
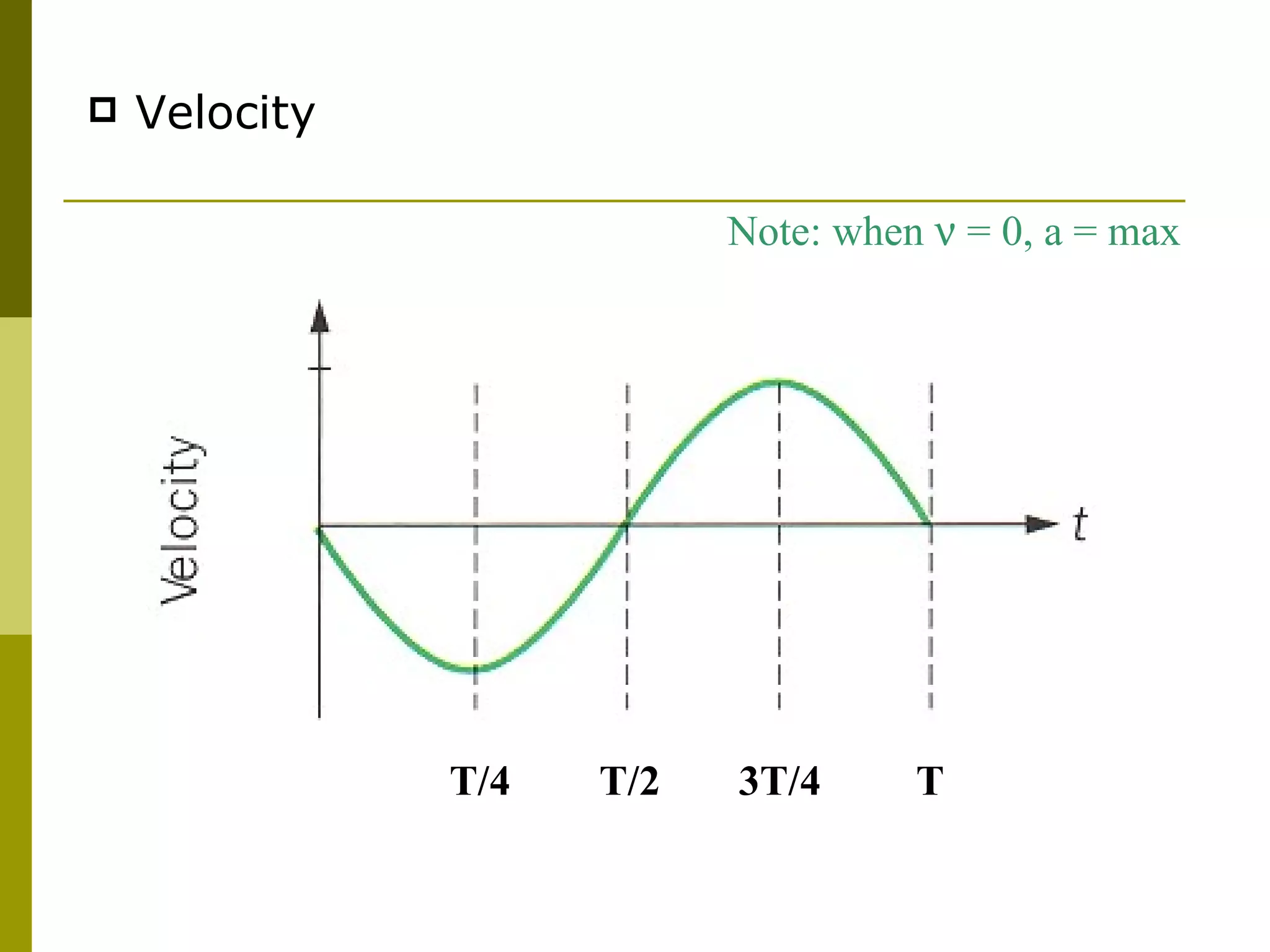
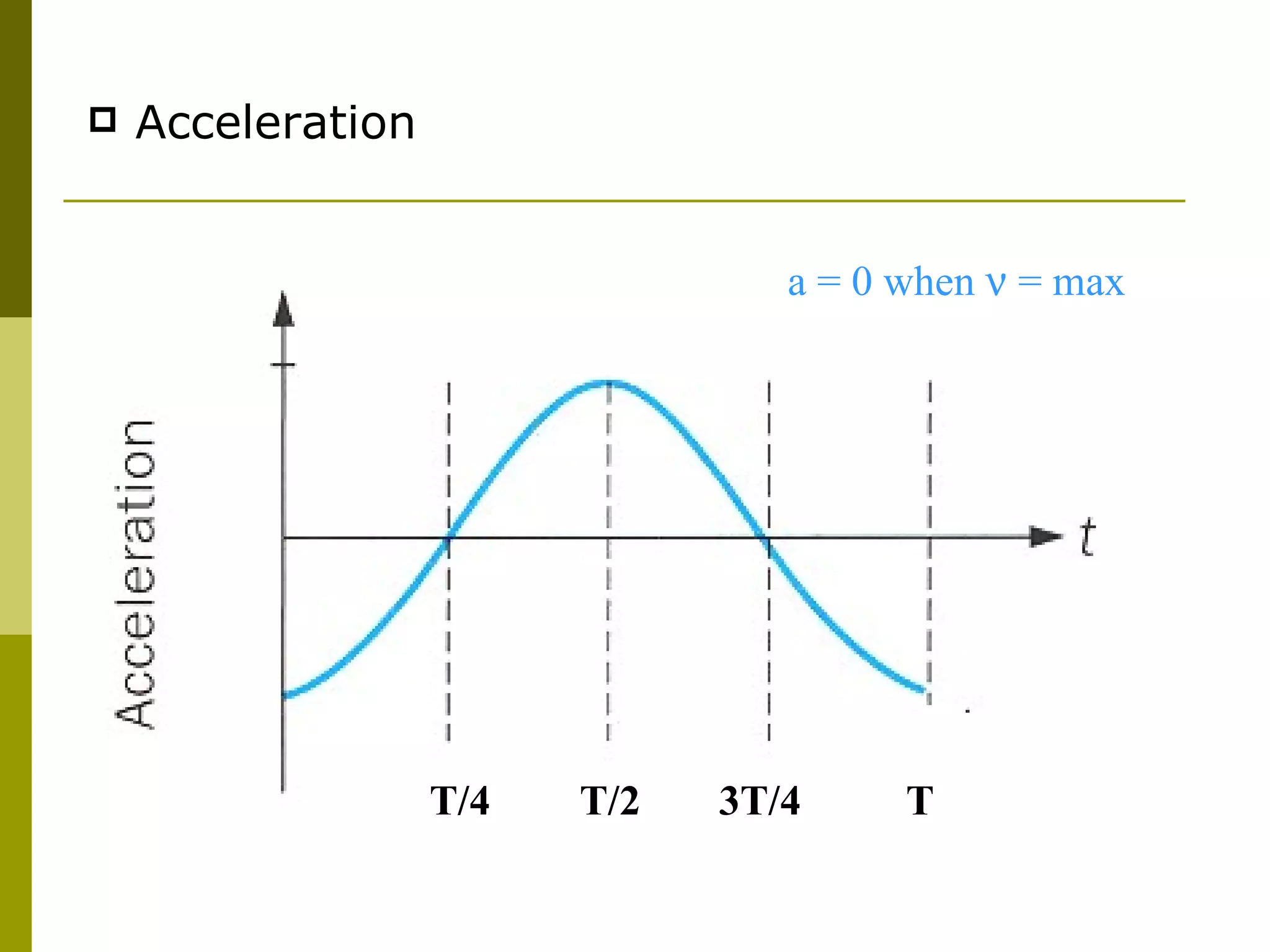
The document links circular motion to simple harmonic motion (SHM) by using the motion of a ball rotating on a turntable to represent circular motion, and the shadow of a pendulum attached to the ball to represent SHM. It derives the equations for displacement, velocity, and acceleration of the pendulum's SHM from the ball's uniform circular motion. The displacement is described by a cosine function, the velocity is described by the square root of a quantity minus the displacement squared, and the acceleration is directly proportional to and opposite in direction from the displacement. All properties vary sinusoidally with time for SHM.

1. 13.1.1 simple harmonic motion Part 2: translating circular motion to simple harmonic

2. Simple harmonic motion Linear motion: a - constant in size + direction Circular motion: a - constant in size only Oscillatory motion: a changes periodically in size + direction (like x and  ) SHM is a special form of oscillating motion Pendulums and masses on springs exhibit SHM A body oscillates with SHM if the displacement changes sinusodially

3. Linking circular motion and SHM The arrangement shown below can be used to demonstrate the link between circular motion and SHM

4. Adjusting the speed of the turntable will allow both shadows to have the same motion (i.e. move in phase) The shadows are the components of each motion parallel to the screen and are sinusoidal Let N represent the sinusoidal motion of one shadow It oscillates about O (equilibrium point) in a straight line between A and B O N A B

5. Displacement and velocity When N is left of O: - x is left -  is left when moving away from O and right when moving towards O When N is right of O: - x is right -  is right when moving away from O and left when moving towards O

6. The size of the restoring force increases with x BUT always acts towards equilibrium point (O) F  - x  resulting acceleration must behave likewise, since F = ma and m is constant i.e. a increases with x but acts towards O a  - x In oscillations a and x always have opposite signs

7. Definition “ If the acceleration of a body is directly proportional to the distance from a fixed point, and is always directed toward that point, then the motion is simple harmonic” a  - x or a = -(+ve constant) x Many mechanical oscillations are nearly simple harmonic, especially at small amplitudes Any system obeying Hooke’s law will exhibit SHM when vibrating

8. Equations of SHM Consider the ball rotating on the turntable The ball moves in a circle of radius r It has uniform angular velocity  The speed, v around the circumference will be constant and equal to  r ( v =  r) At time t the ball (and hence the bob of the pendulum) are in the positions shown:

10. Displacement Angle  =  t (since  =  /t) The displacement of the ball along OF from O is given by: x = r cos  = r cos  t For the pendulum (and masses on springs), the radius of the circle is equal to the amplitude of its oscillation i.e. r = A Hence x = A cos  t But  = 2  f x = A cos 2  f t  r x

12. Velocity The velocity of the pendulum bob is equal to the component of the ball’s velocity parallel to the screen (i.e. along y-axis) Bob Ball  v =  r O  r  velocity = - v sin  Ball Bob

13. Velocity of bob = - v sin  = -  r sin   =  /t   =  t Velocity of pendulum bob,  = -  r sin  t Sin  is +ve when 0 °    180° (i.e. bob or ball moving down) Sin  is –ve when 180 °    360° (bob or ball moving up) Negative sign ensures velocity is negative when moving down and positive when moving up!

14. Variation of velocity with displacement sin 2  + cos 2  = 1  sin  =  (1- cos 2  )  = ±  r sin    = ±  r  (1- cos 2  ) From earlier x = r cos  , so x /r = cos   ( x /r) 2 = cos 2 

15. By substituting: Velocity = ±  r  (1- cos 2  ) = ±  r  (1 - ( x /r) 2 ) = ±   (r 2 – x 2 ) Recall  = 2  f Hence velocity of pendulum in SHM of amplitude A is given by:  = ± 2  f  (A 2 – x 2 )

16. Acceleration The acceleration of the bob is equal to the component of the acceleration of the ball parallel to the screen The acceleration of the ball, a =  2 r towards O So the component of a along OF =  2 r cos   Bob Ball a =  2 /r a =  2 r cos  O  O

17. Hence, the acceleration of the bob is given by: a = -  2 r cos  (-ve since moving down) Since x = r cos  and  = 2  f a = -(2  f ) 2 x Since (2  f ) 2 or  2 is a +ve constant, equation states that acceleration of the bob towards the equilibrium point O is proportional to the displacement x from O The acceleration is zero at O and maximum when the bob is at the limits of its motion when the direction and motion changes

18. Time period Period T is time taken for the bob to complete one oscillation In the same time the ball has made one revolution of the turntable  T = circumference of circle speed of ball T = 2  r 

19. Since  = r  T = 2   For a particular SHM  is constant and independent of the amplitude (or radius) of the oscillation If the amplitude increases, the body travels faster  T is unchanged A motion with constant T, whatever the amplitude, is isochronous - this is an important characteristic of SHM

20. Time traces of SHM Displacement T/4 T/2 3T/4 T Note: the gradient = velocity

21. Velocity T/4 T/2 3T/4 T Note: when  = 0, a = max

22. Acceleration T/4 T/2 3T/4 T a = 0 when  = max

23. All graphs are sinusoidal When the velocity is zero, the acceleration is a maximum and vice versa There is a phase difference between them Between  and a phase difference = T/4 Between x and a phase difference = T/2

24. Summary: equations of SHM Frequency f =  /2  Period T = 2  /  Displacement x = A cos  t = A cos 2  f t Velocity  =    A 2 – x 2 =  2  f  A 2 – x 2 Acceleration a = -(2  f ) 2 x