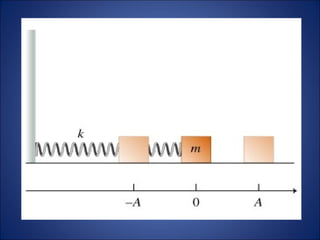
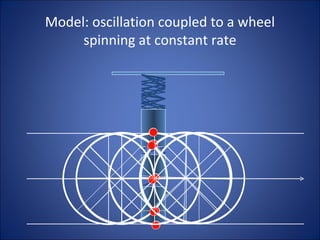
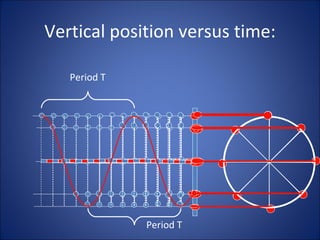
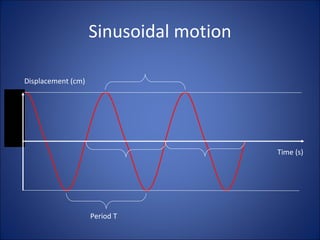
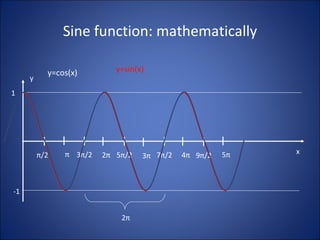
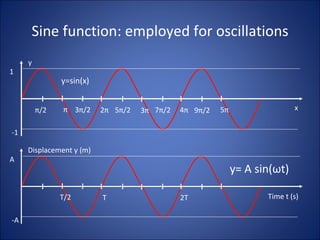
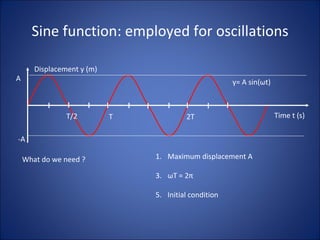
Simple harmonic motion (SHM) describes the motion of an object undergoing displacement from an equilibrium position due to a restoring force proportional to the displacement. The motion is periodic and sinusoidal, with the displacement following the equation x=A sin(ωt+φ), where A is the amplitude, ω is the angular frequency, t is time, and φ is the phase. Examples of SHM include a mass attached to a spring and the pendular motion of a mass hanging from a fixed point by a string.

1. Presented By : Himanshu K. Khanna FAITH ACADEMY

3. where, x  Displacement A  Amplitude of the oscillation f  Frequency t  Elapsed time ф  Phase of oscillation If there is no displacement at time t = 0, the phase is ф = π /2

12. A mass is oscillating on a spring Position in equal time intervals:

15. Model: oscillation coupled to a wheel spinning at constant rate

16. Vertical position versus time: Period T Period T

17. Sinusoidal motion Time (s) Displacement (cm) Period T

18. Sine function: mathematically x y 2 π -1 1 y=sin(x) y=cos(x) π /2 π 3 π /2 2 π 5 π /2 3 π 7 π /2 4 π 9 π /2 5 π

19. Sine function: employed for oscillations Time t (s) Displacement y (m) -A A y= A sin( ω t) x y π /2 π 3 π /2 2 π 5 π /2 3 π 7 π /2 4 π 9 π /2 5 π -1 1 y=sin(x) T/2 T 2T