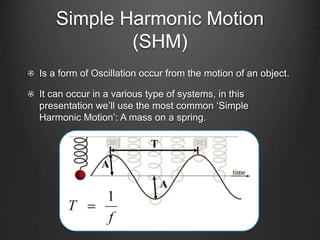
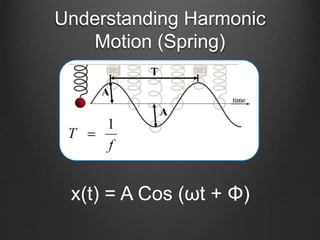
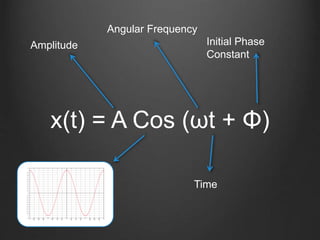
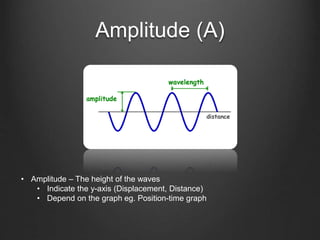
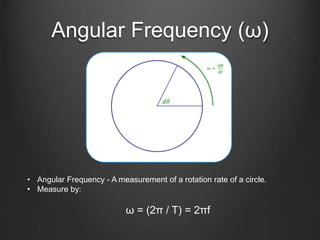
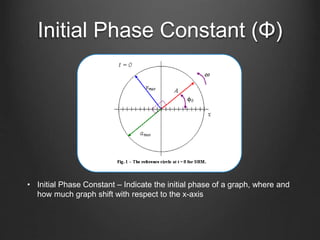
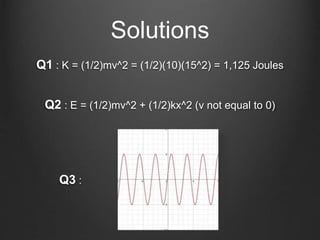
This document discusses energy conservation in simple harmonic motion using a mass on a spring as an example. It explains that the total energy in the system remains constant and is equal to the sum of kinetic and potential energy. Three cases are presented where the mass is at different positions on the spring: initially held at a stretched position x=X, after being released from x=X, and initially held at a compressed position x=-X. The expression for simple harmonic motion x(t)=Acos(ωt+Φ) is also defined, where A is amplitude, ω is angular frequency, and Φ is the initial phase constant. Three sample questions are provided to test understanding.

1. Energy Conservation – Spring

2. Simple Harmonic Motion
(SHM)
Is a form of Oscillation occur from the motion of an object.
It can occur in a various type of systems, in this
presentation we’ll use the most common ‘Simple
Harmonic Motion’: A mass on a spring.

3. Energy Conservation
Ideal Condition : Absent of friction
Total Energy (E) = Kinetic Energy (K) + Potential Energy
(U)
Kinetic Energy = (1/2)mv^2
Potential Energy of the spring = (1/2)kx^2
Therefore, E = (1/2)mv^2 + (1/2)kX^2

4. 1st Case
• Considering these following
cases, where x = 0 is the initial
point.
• The object mass (m) is held
stationary at the position x = X
• By doing so the work has
been done on the object and
stored as a potential energy
(U)
• Because V = 0 (Object is
stationary)
• Kinetic energy (K) = 0
E = K + U = (1/2)mv^2 + (1/2)kX^2
K = 0
Therefore,
E = 0 + (1/2)kX^2

5. 2nd Case
• After the object mass (m) get
released the object move due
to the force stored in the
potential energy (U)
• Since the object is moving
the energy is converted
from potential energy (U)
to kinetic energy (K)
• Therefore, Potential
Energy (U) = 0
E = K + U = (1/2)mv^2 + (1/2)kX^2
U = 0
Therefore,
E = (1/2)m(-v^2) + 0
E = (1/2)mv^2 + 0

6. 3rd Case
• The object mass (m) is
stationary at the position x = -X
• By doing so the work has
been done on the object and
stored as a potential energy
(U)
• Because V = 0 (Object is
stationary)
• Kinetic energy (K) = 0
E = K + U = (1/2)mv^2 + (1/2)kX^2
K = 0
Therefore,
E = 0 + (1/2)k(-X^2)
E = 0 + (1/2)kX^2

7. Understanding Harmonic
Motion (Spring)
x(t) = A Cos (ωt + Φ)

8. x(t) = A Cos (ωt + Φ)
Amplitude
Angular Frequency
Initial Phase
Constant
Time

9. Amplitude (A)
• Amplitude – The height of the waves
• Indicate the y-axis (Displacement, Distance)
• Depend on the graph eg. Position-time graph

10. Angular Frequency (ω)
• Angular Frequency - A measurement of a rotation rate of a circle.
• Measure by:
ω = (2π / T) = 2πf

11. Initial Phase Constant (Φ)
• Initial Phase Constant – Indicate the initial phase of a graph, where and
how much graph shift with respect to the x-axis

12. Q1 : A mass of 10 kg oscillating on a spring passes
through its equilibrium point with a velocity of 15 m/s.
What is the energy of the system at this point?
Questions
Q2 : A box mass of m kg is moving to the left at a
velocity of v m/s due to the force from the spring. The
spring is not fully stretched. Express this in a formula.
Q3 : Sketch a graph of f where Amplitude = 5, Angular
Frequency = 2 and Initial Phase constant = 5

13. Q1 : K = (1/2)mv^2 = (1/2)(10)(15^2) = 1,125 Joules
Solutions
Q2 : E = (1/2)mv^2 + (1/2)kx^2 (v not equal to 0)
Q3 :