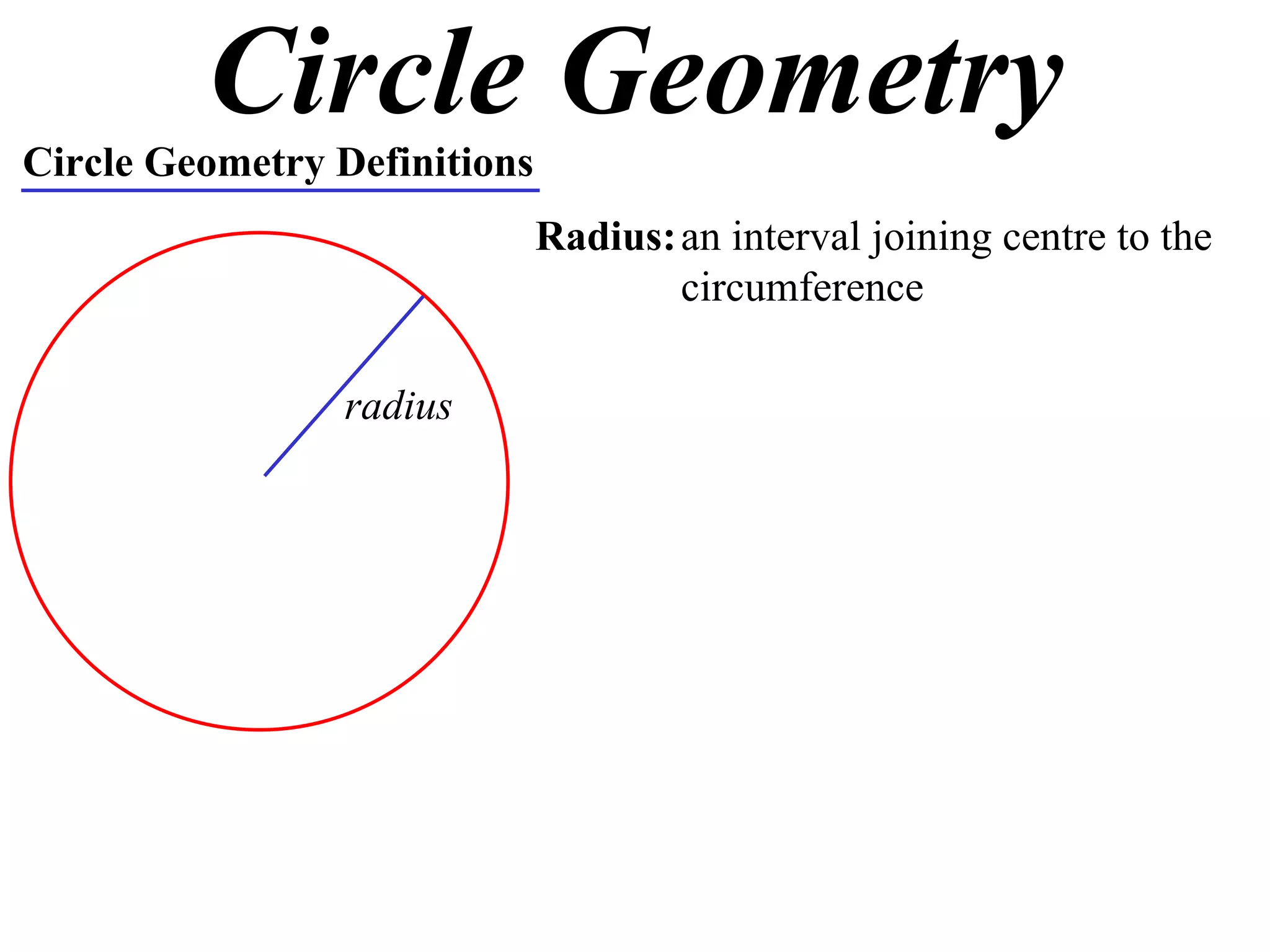
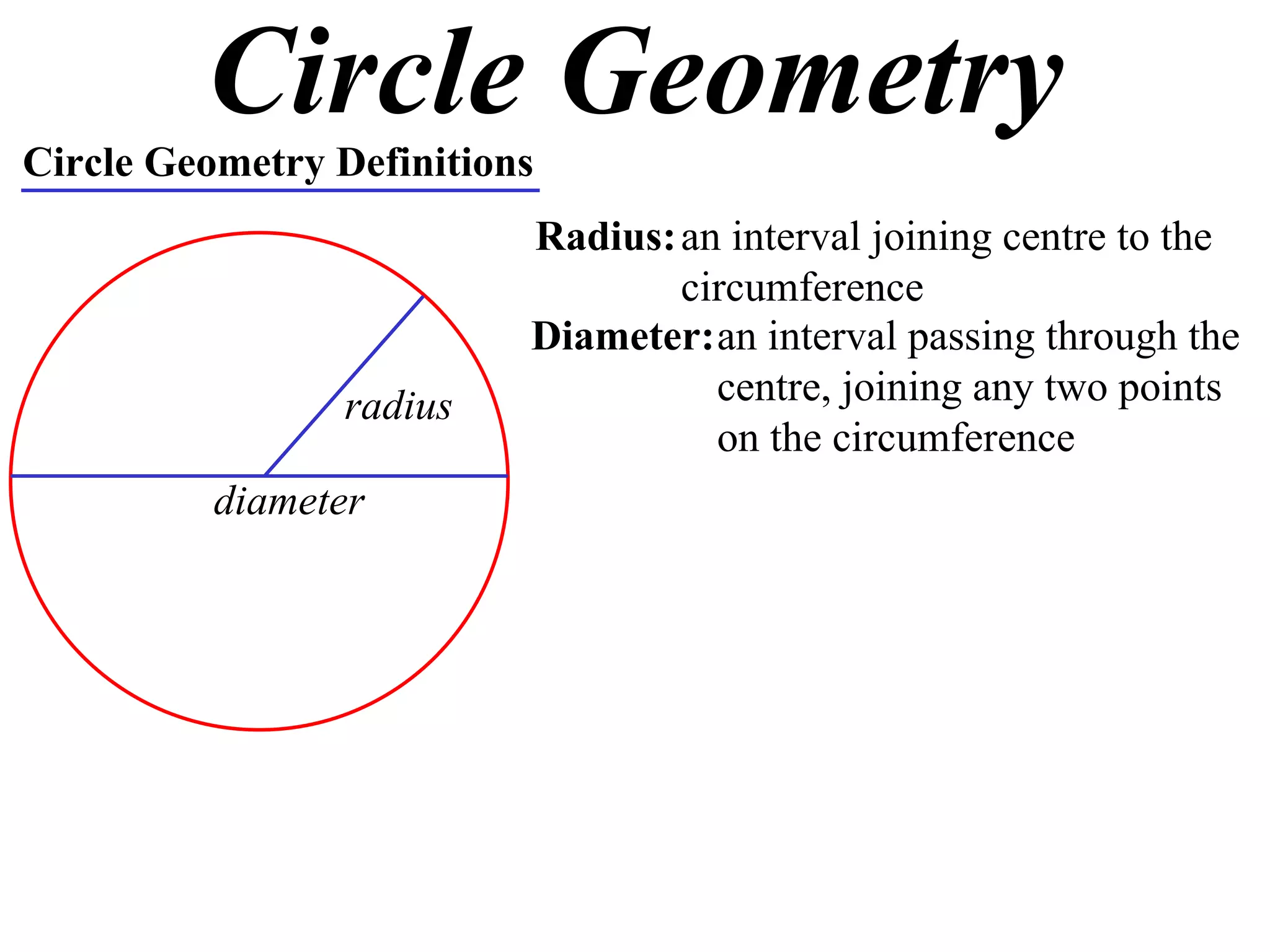
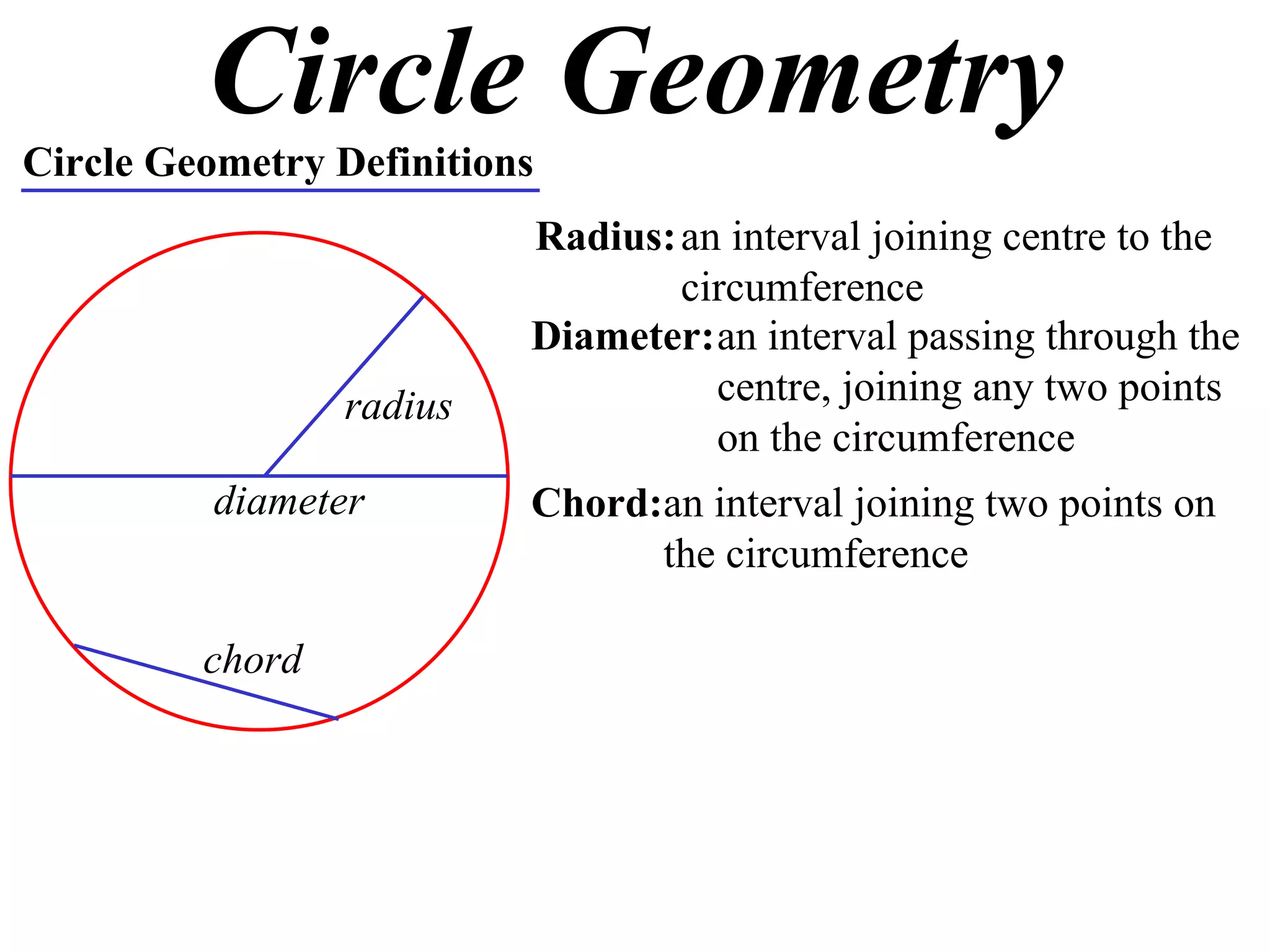
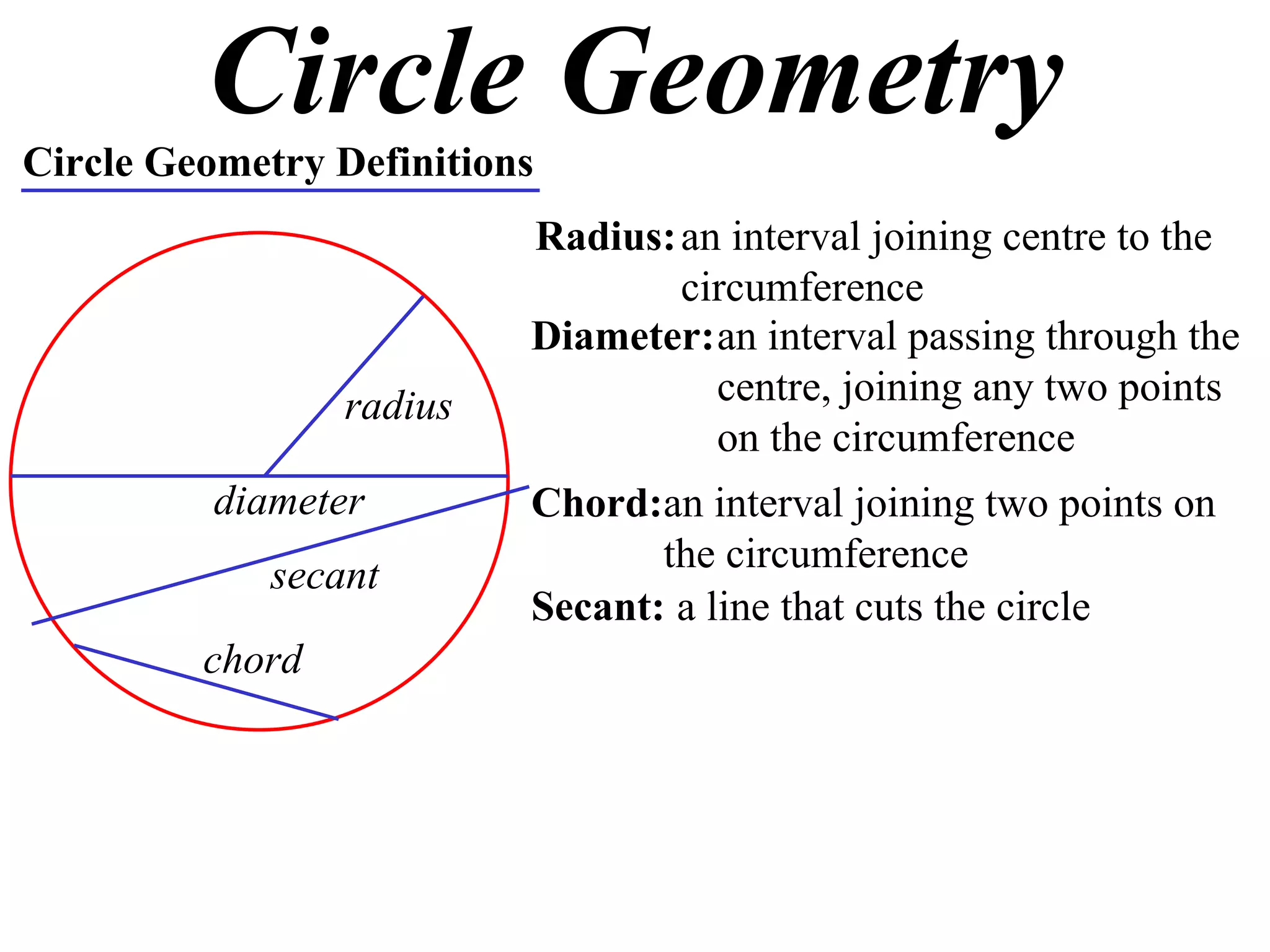
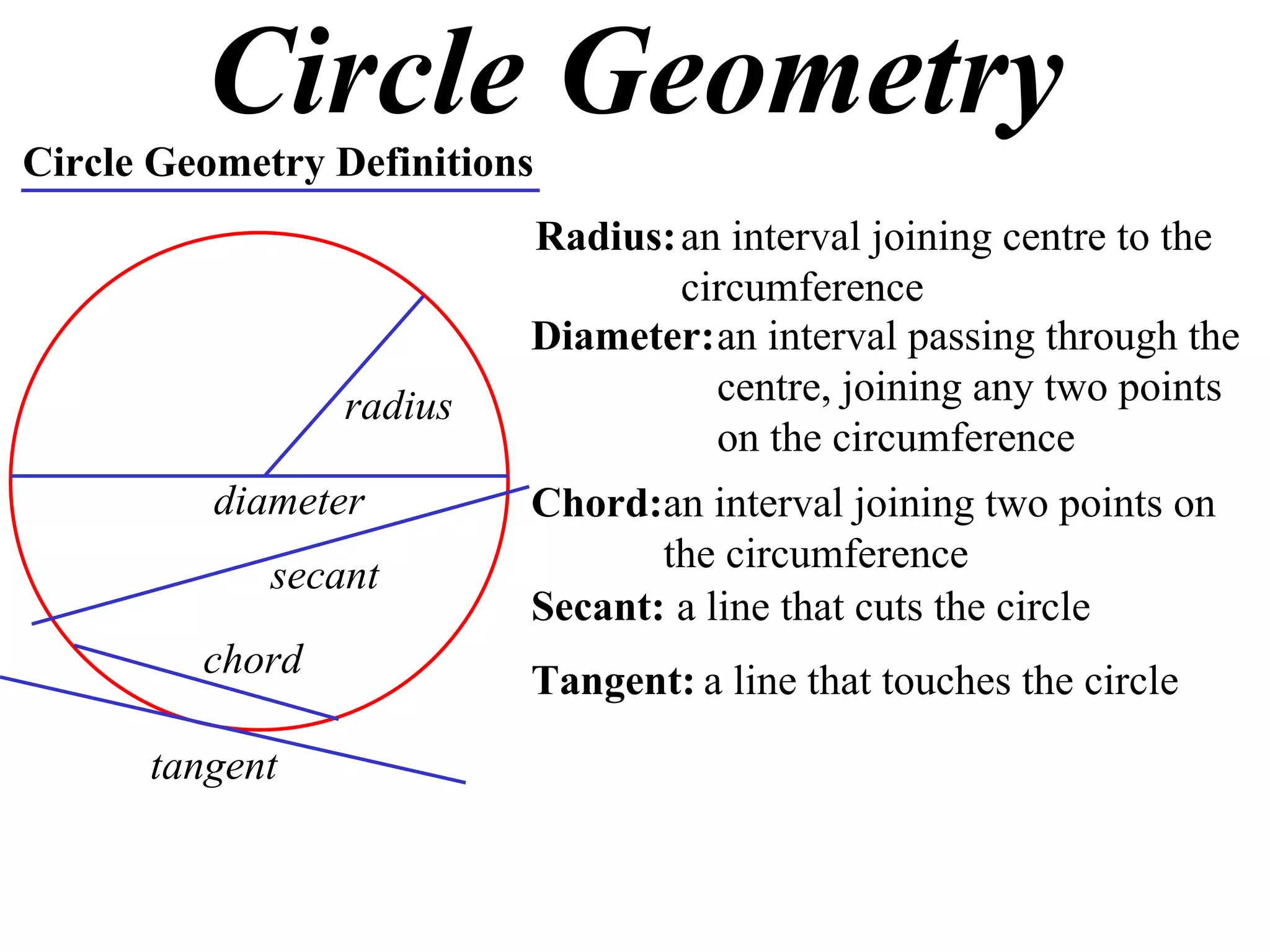
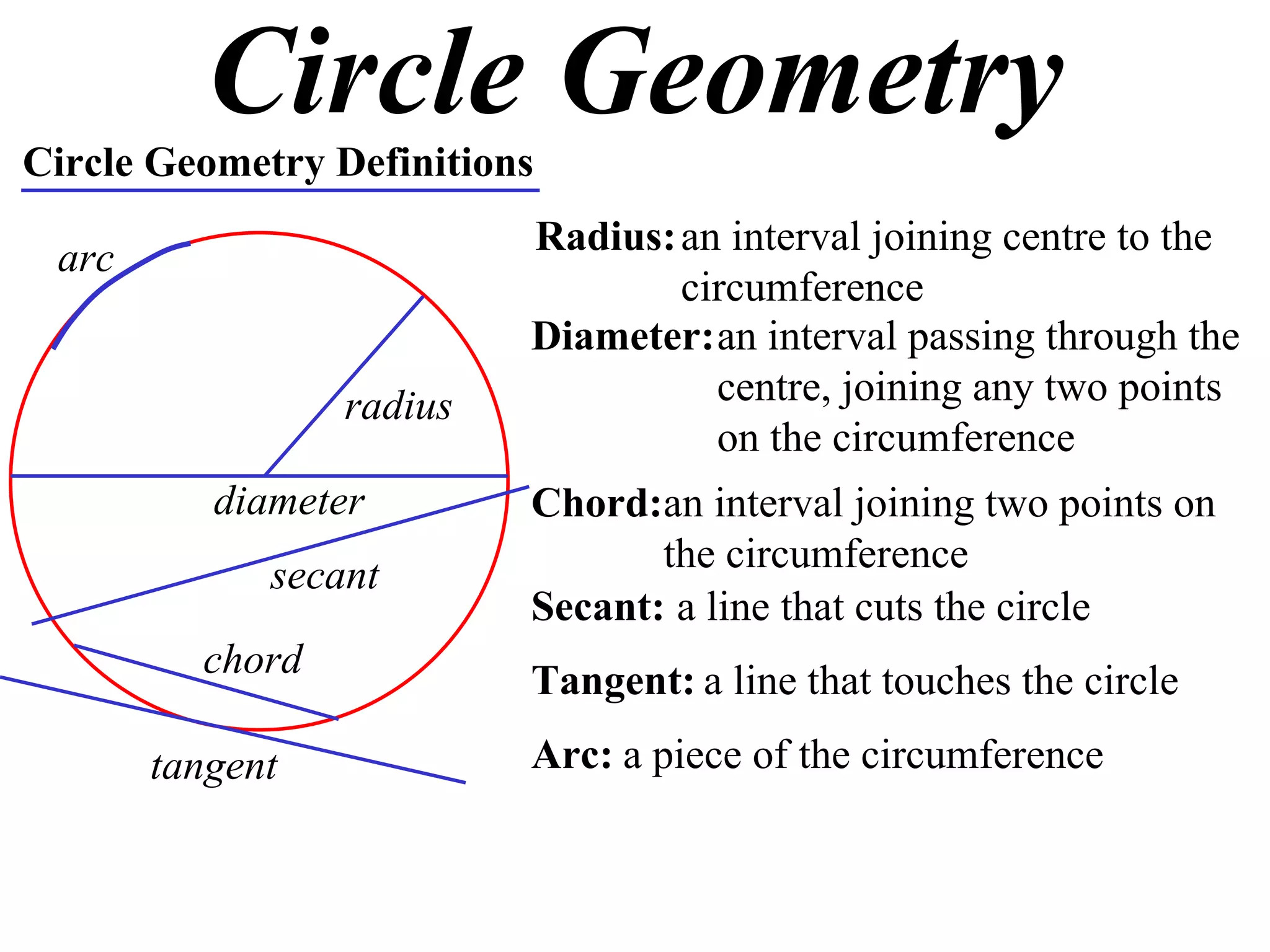
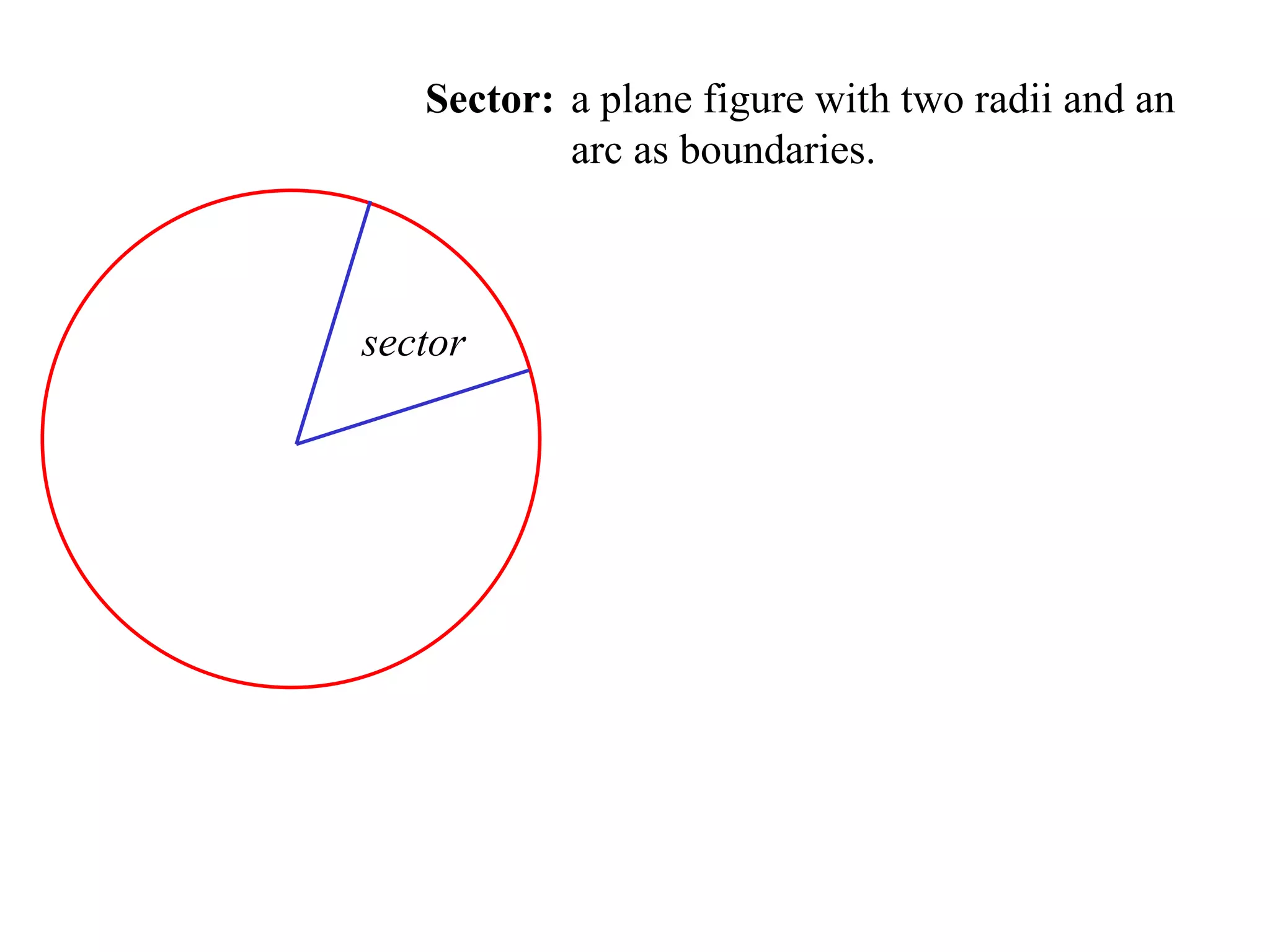
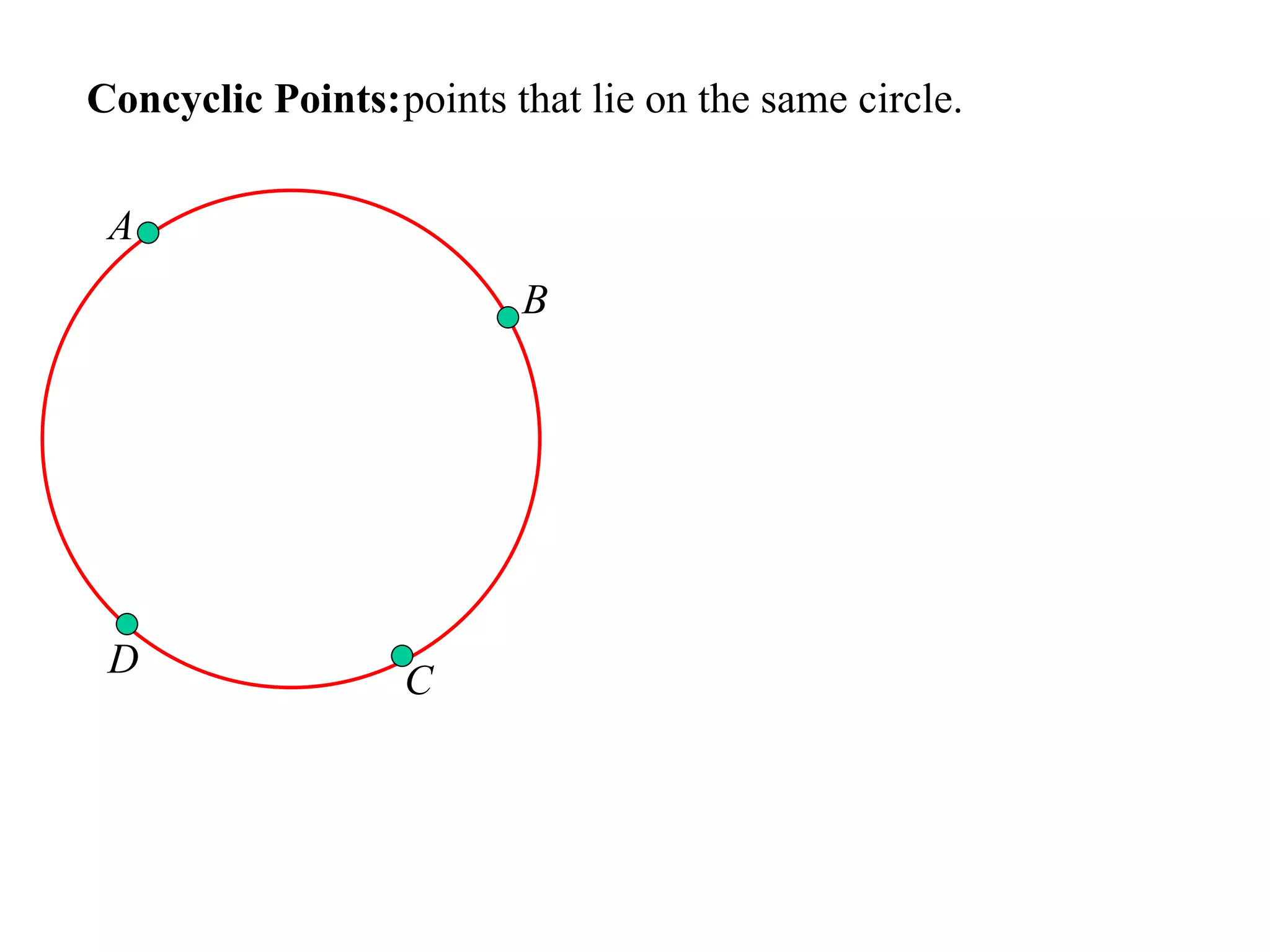
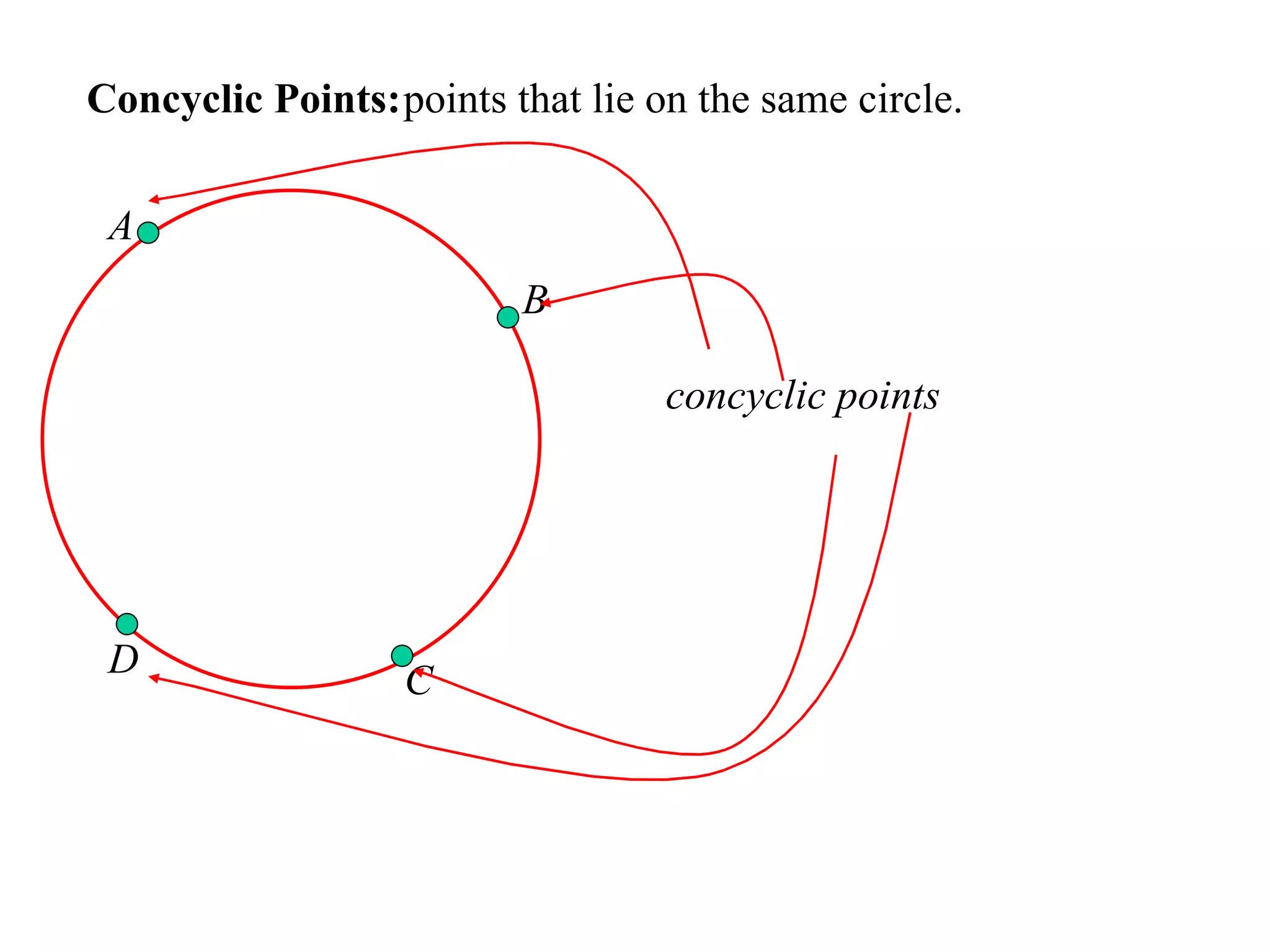
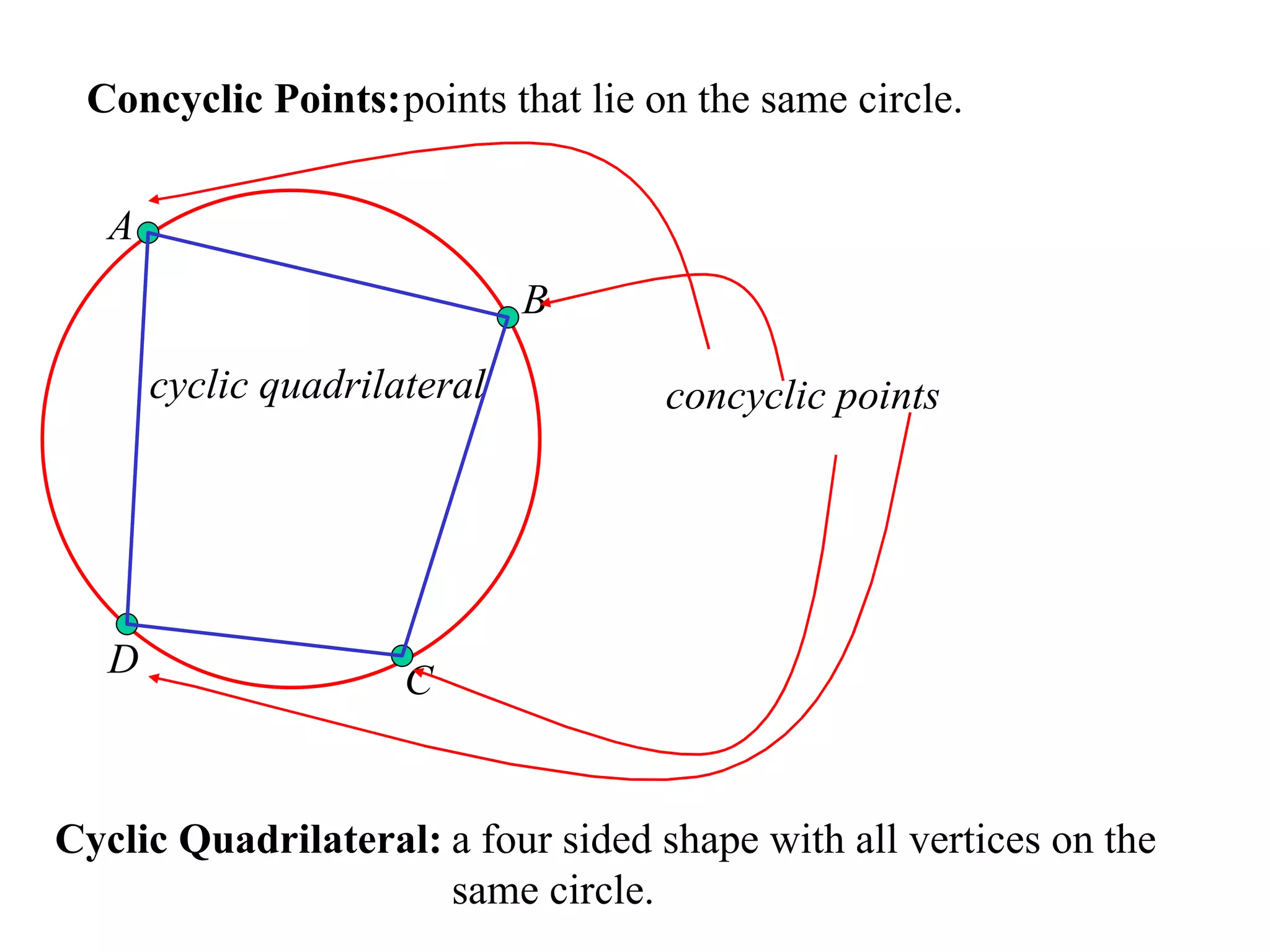
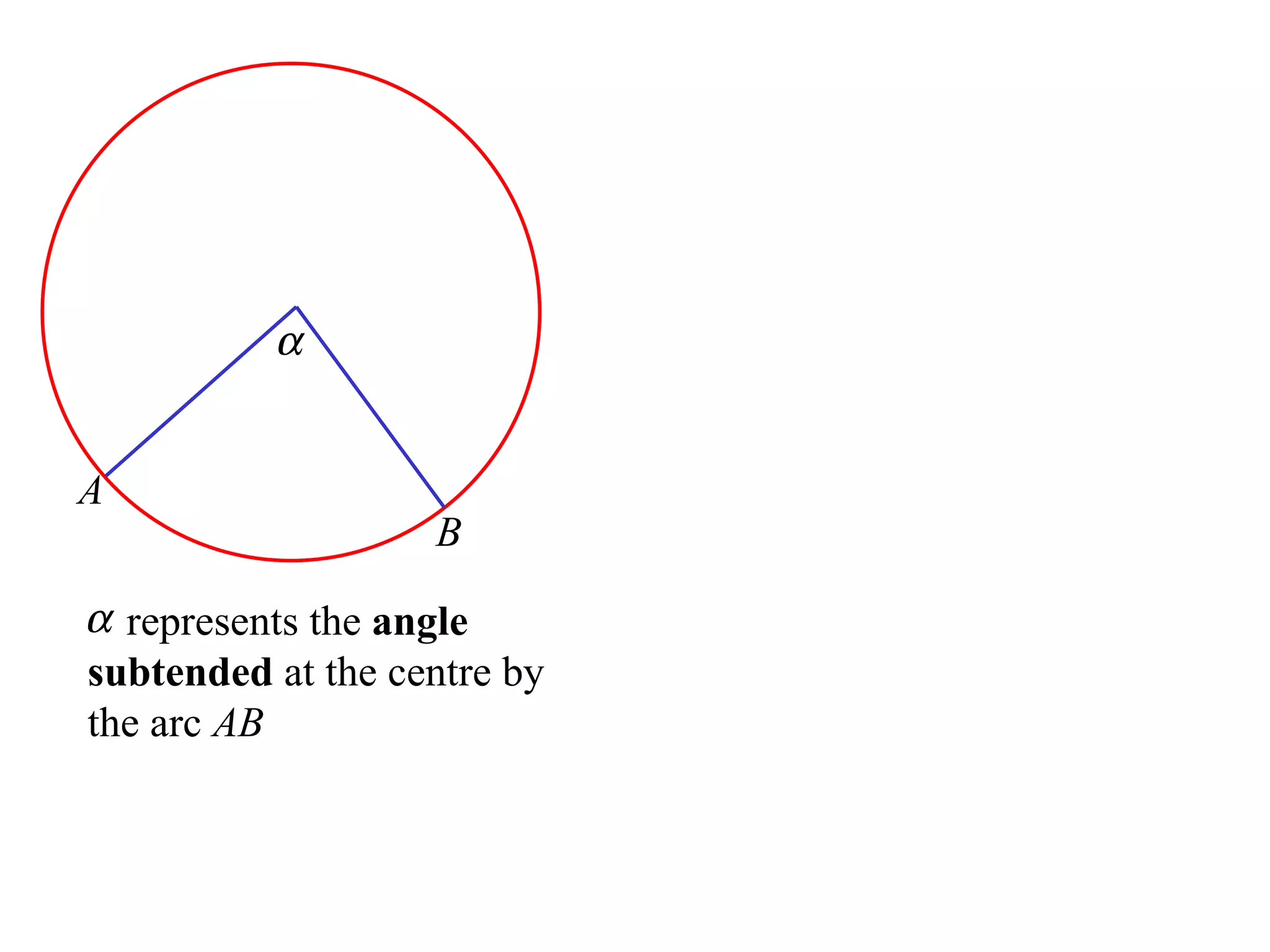
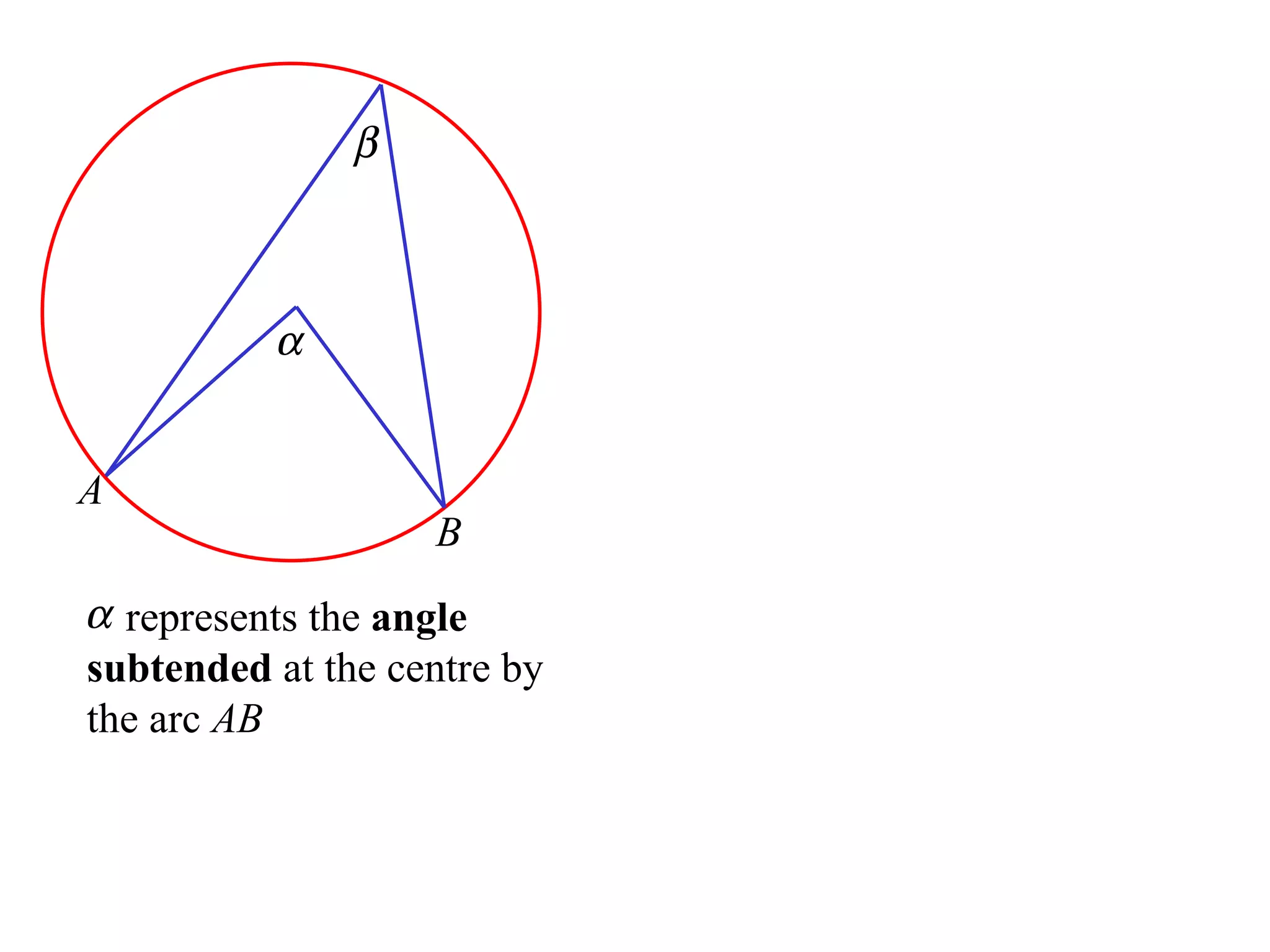
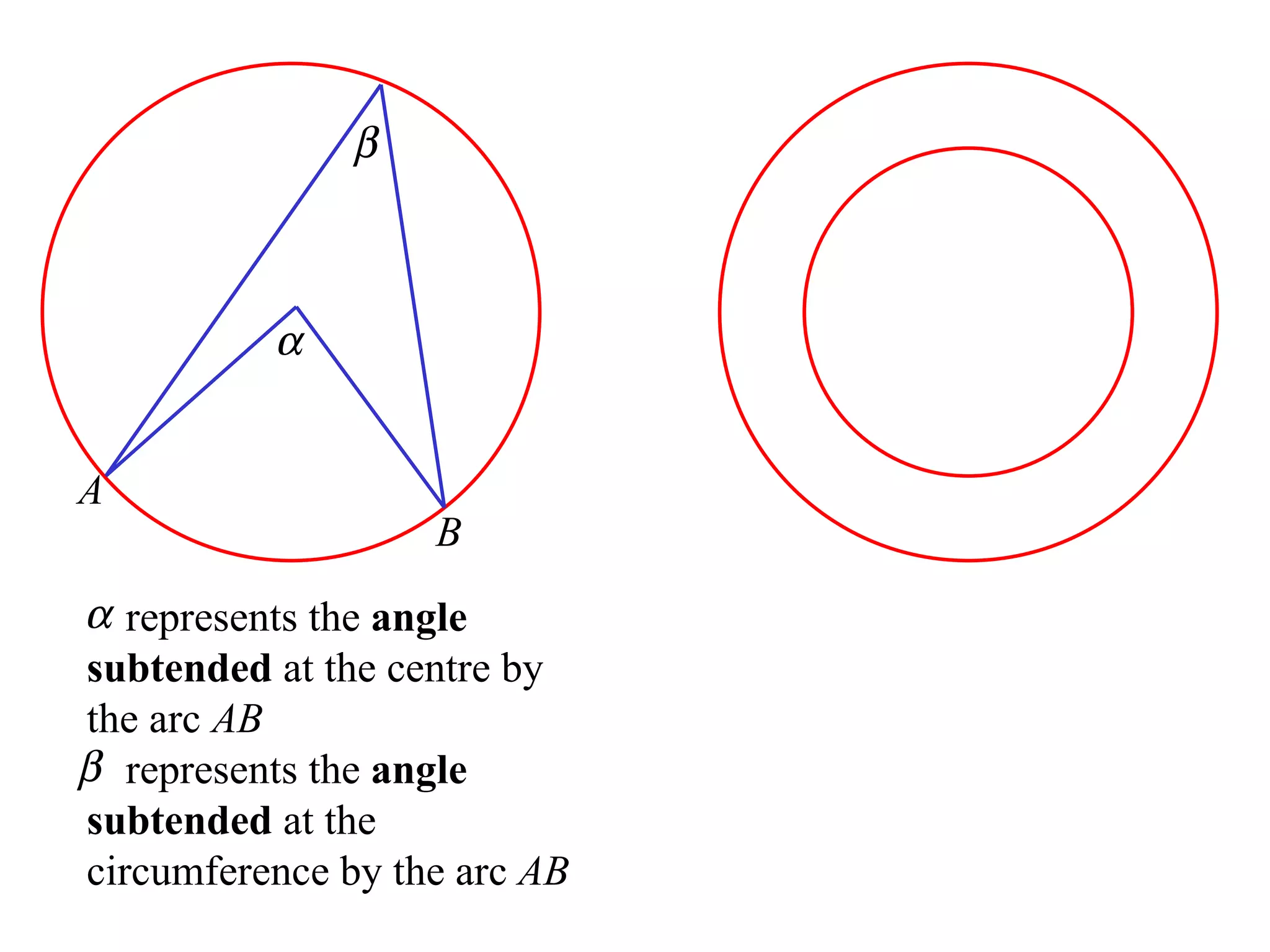
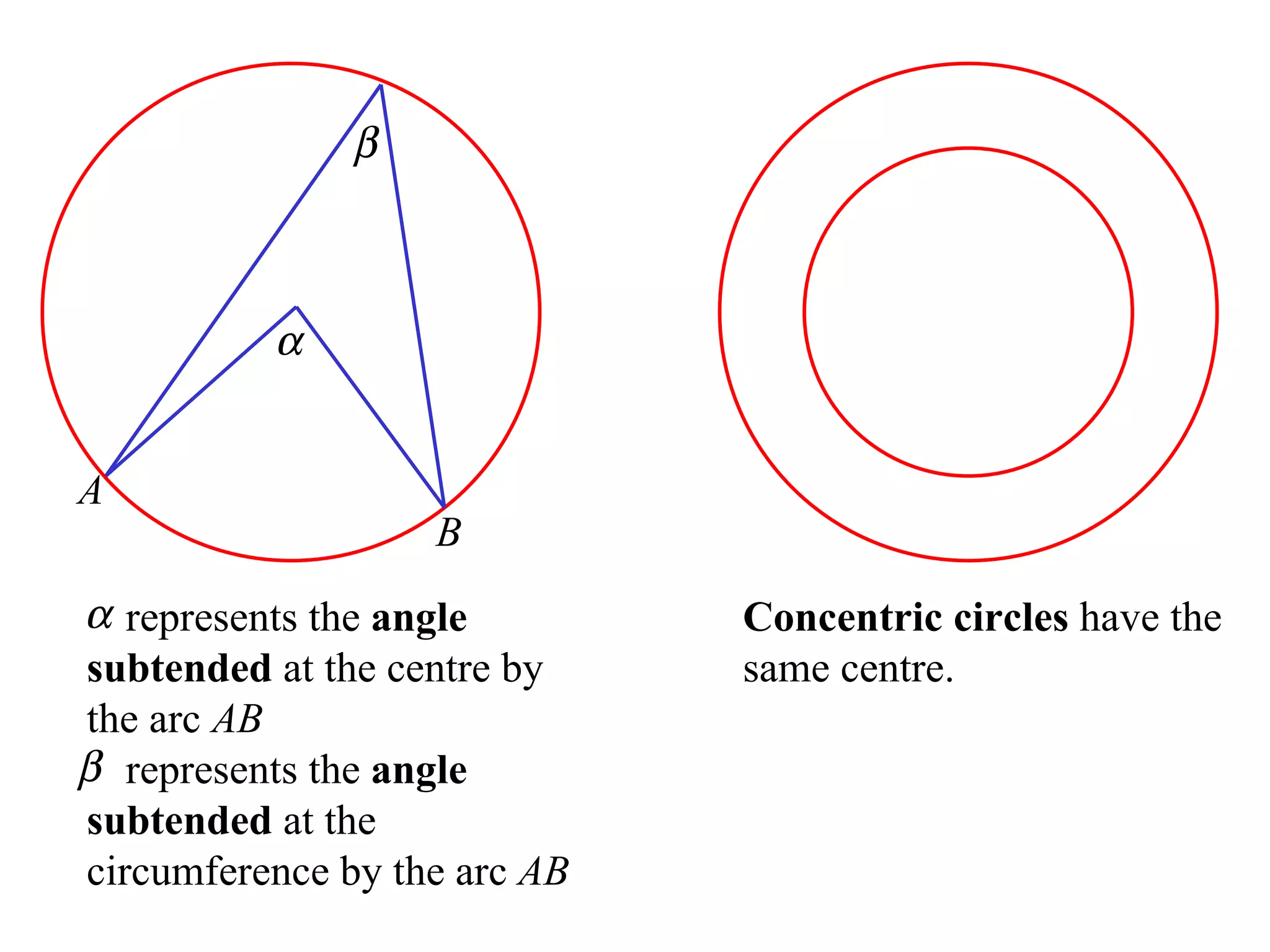
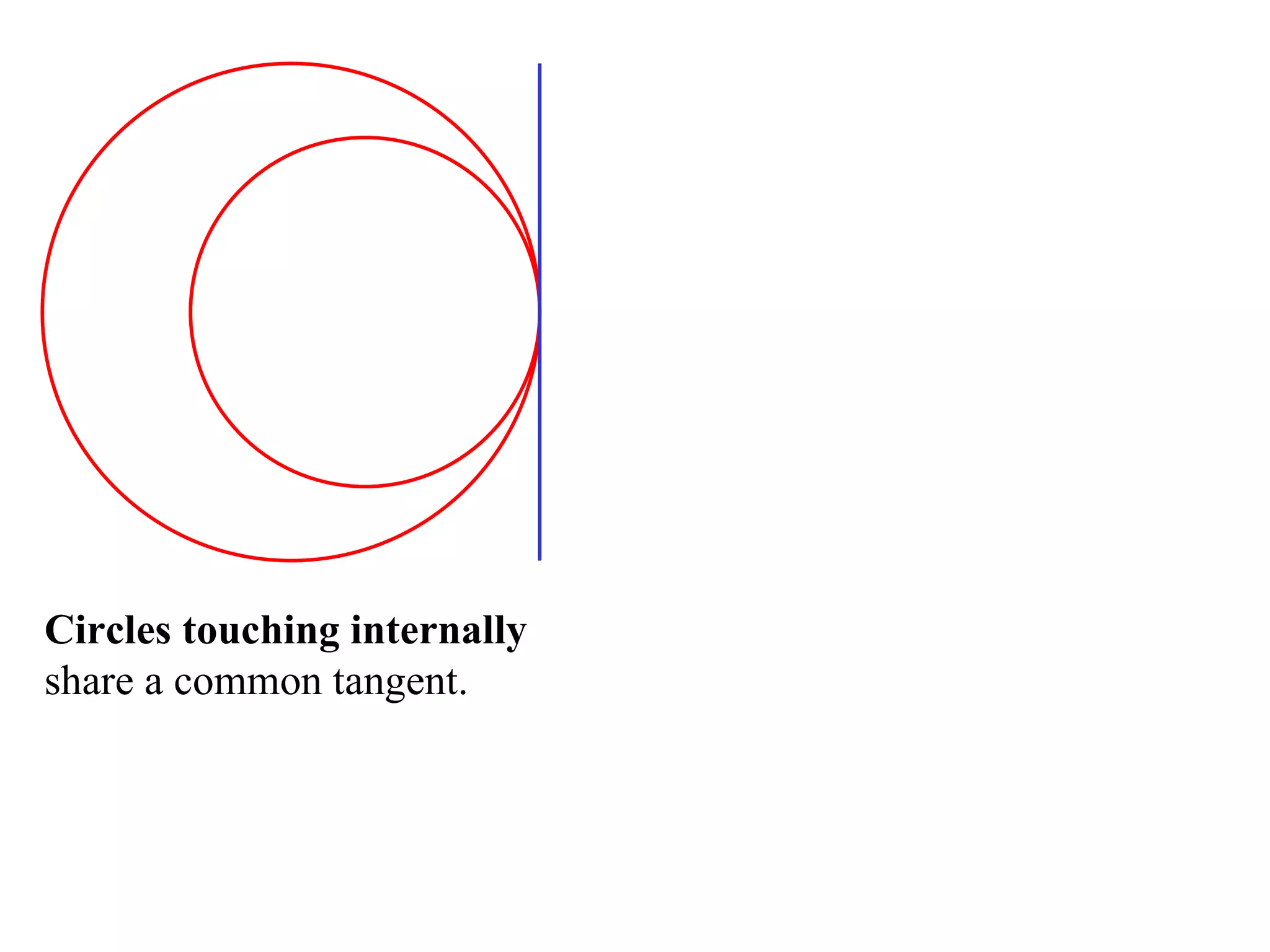
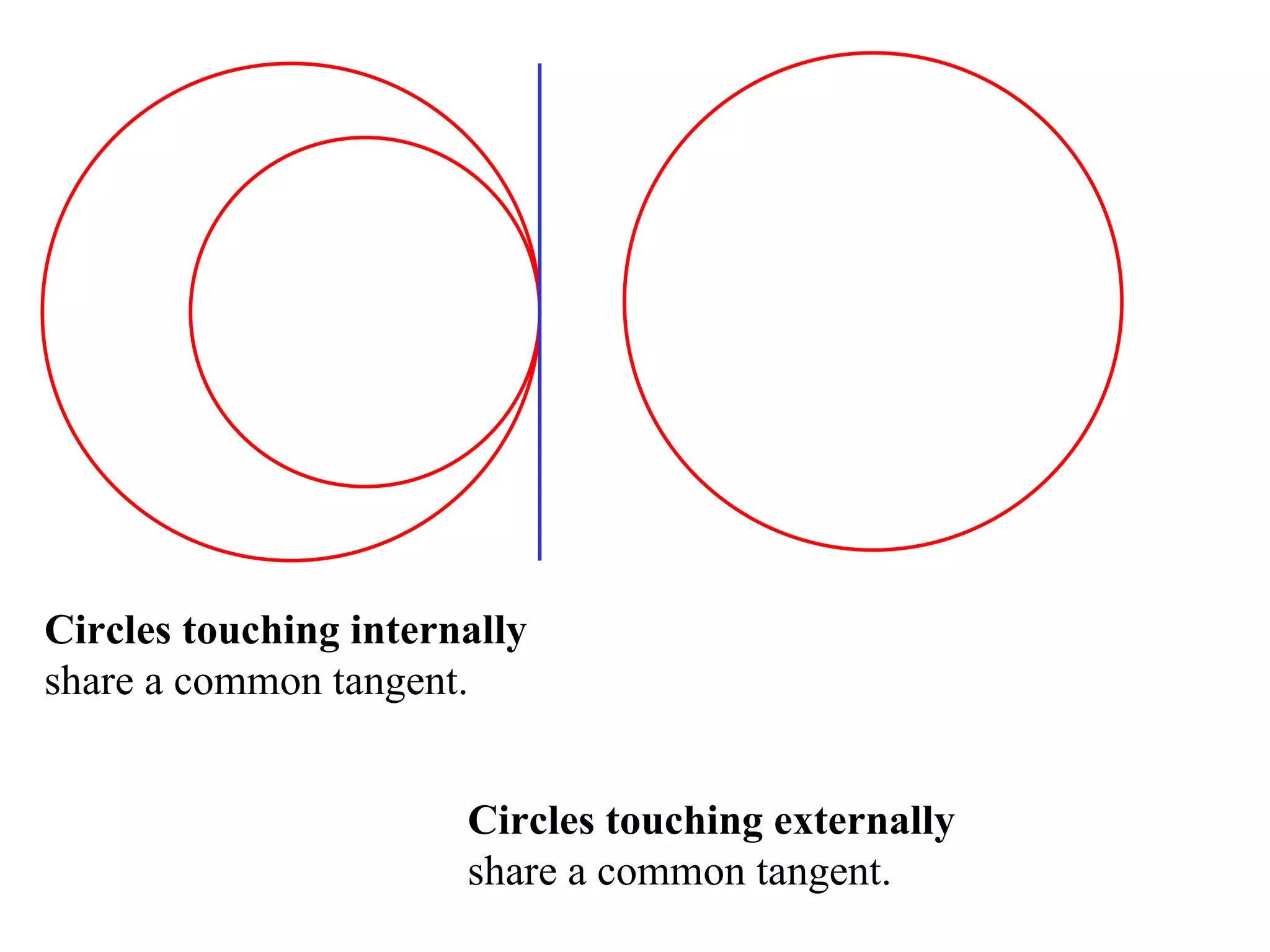
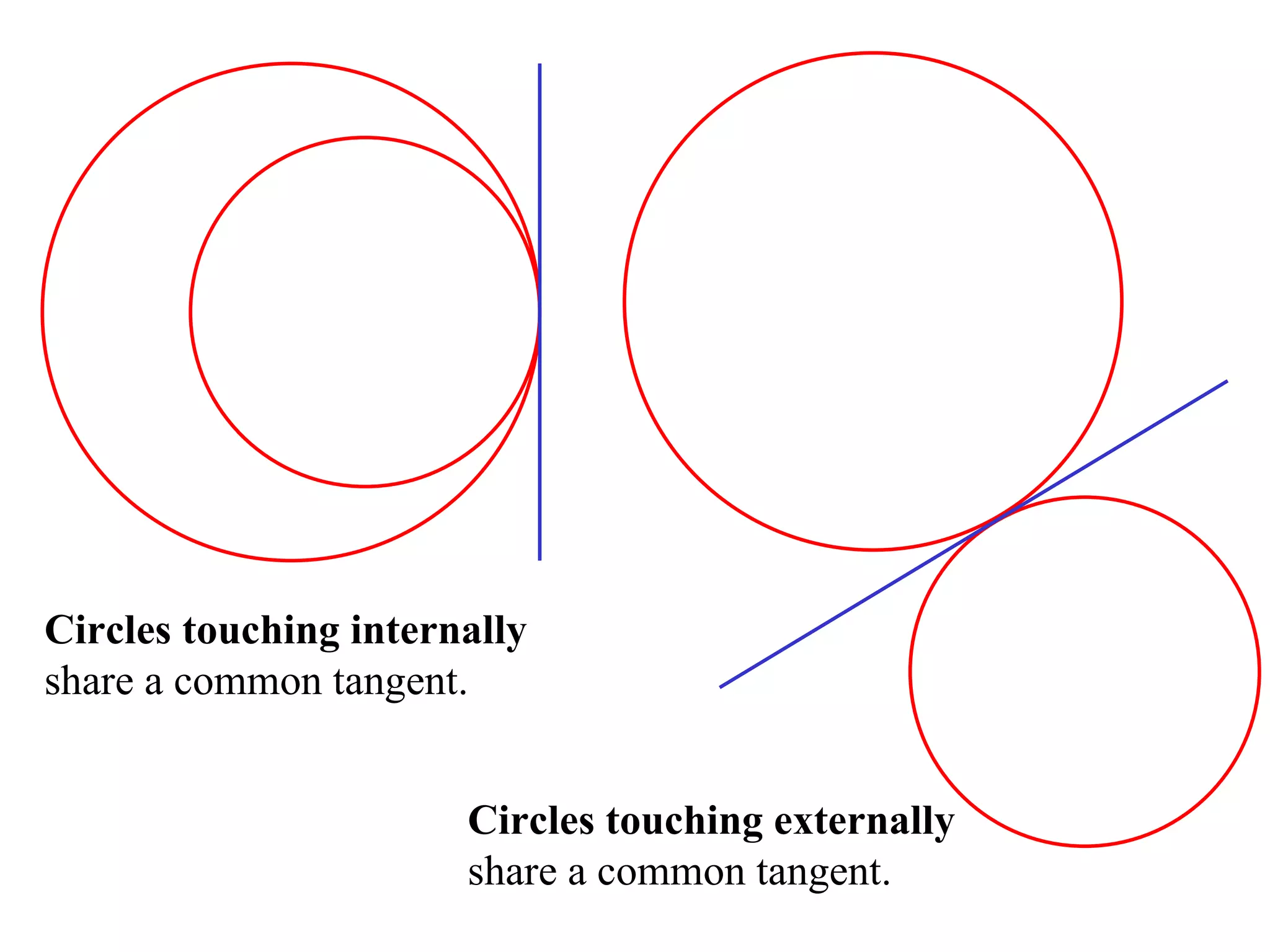
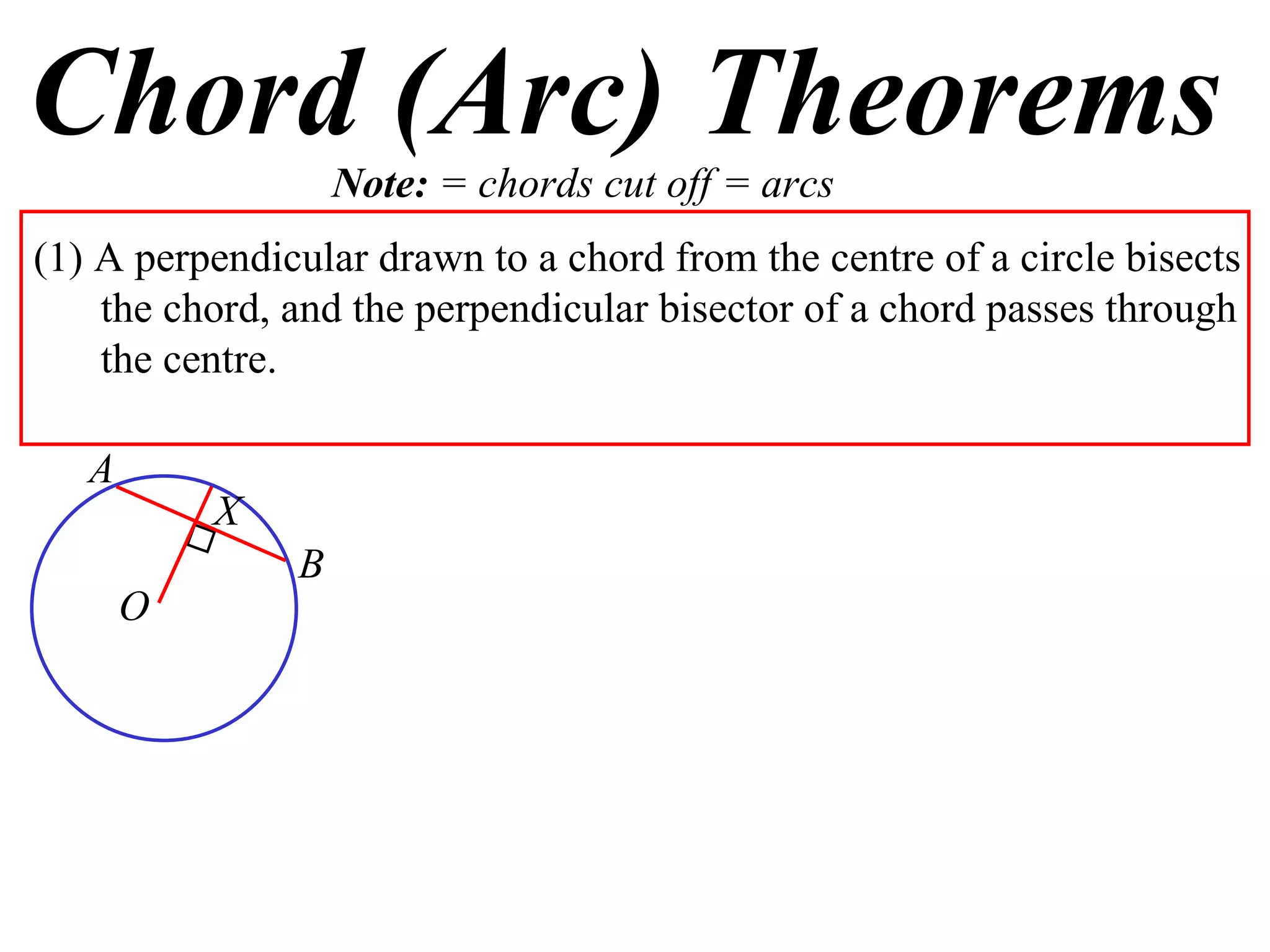
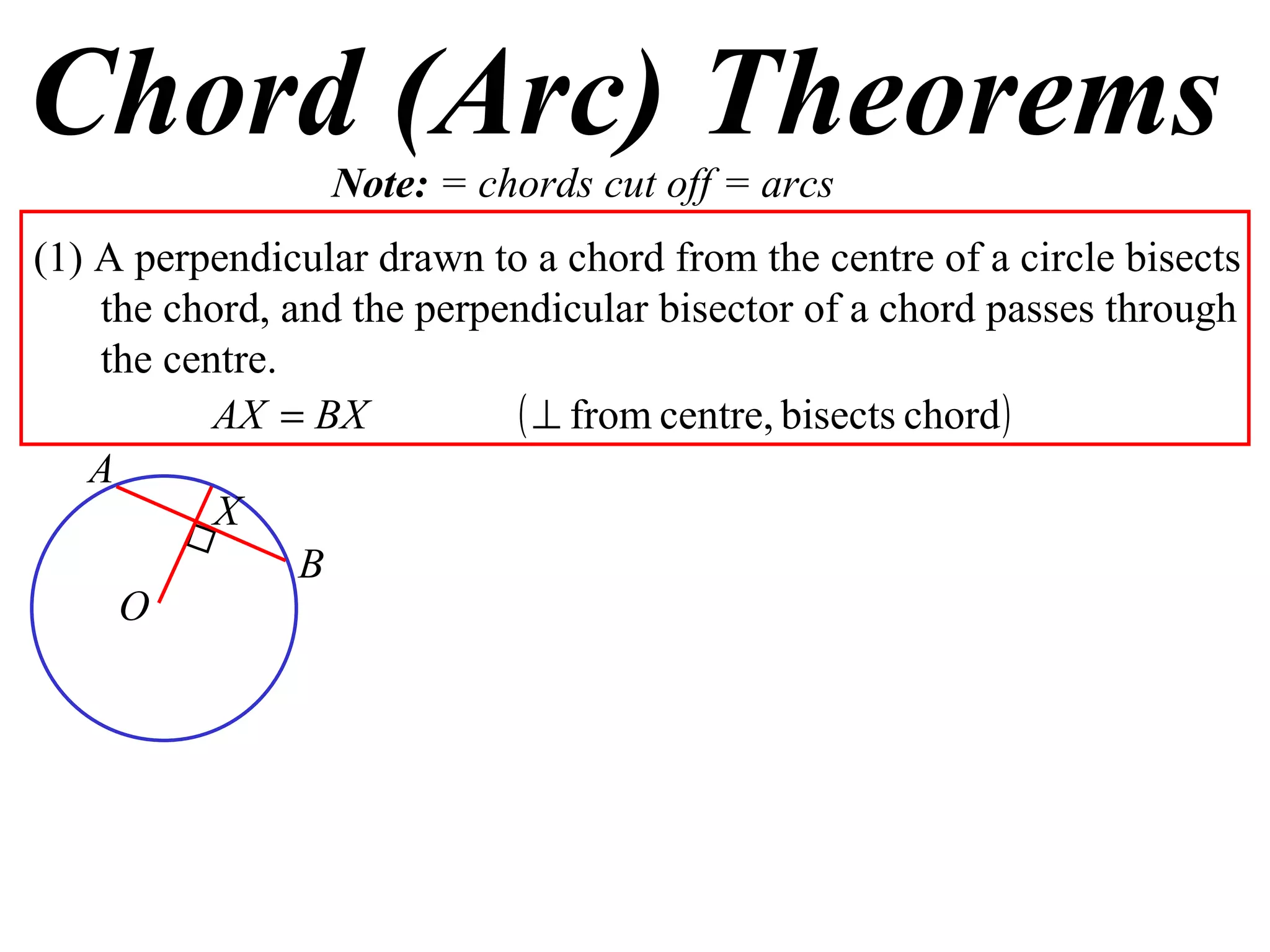
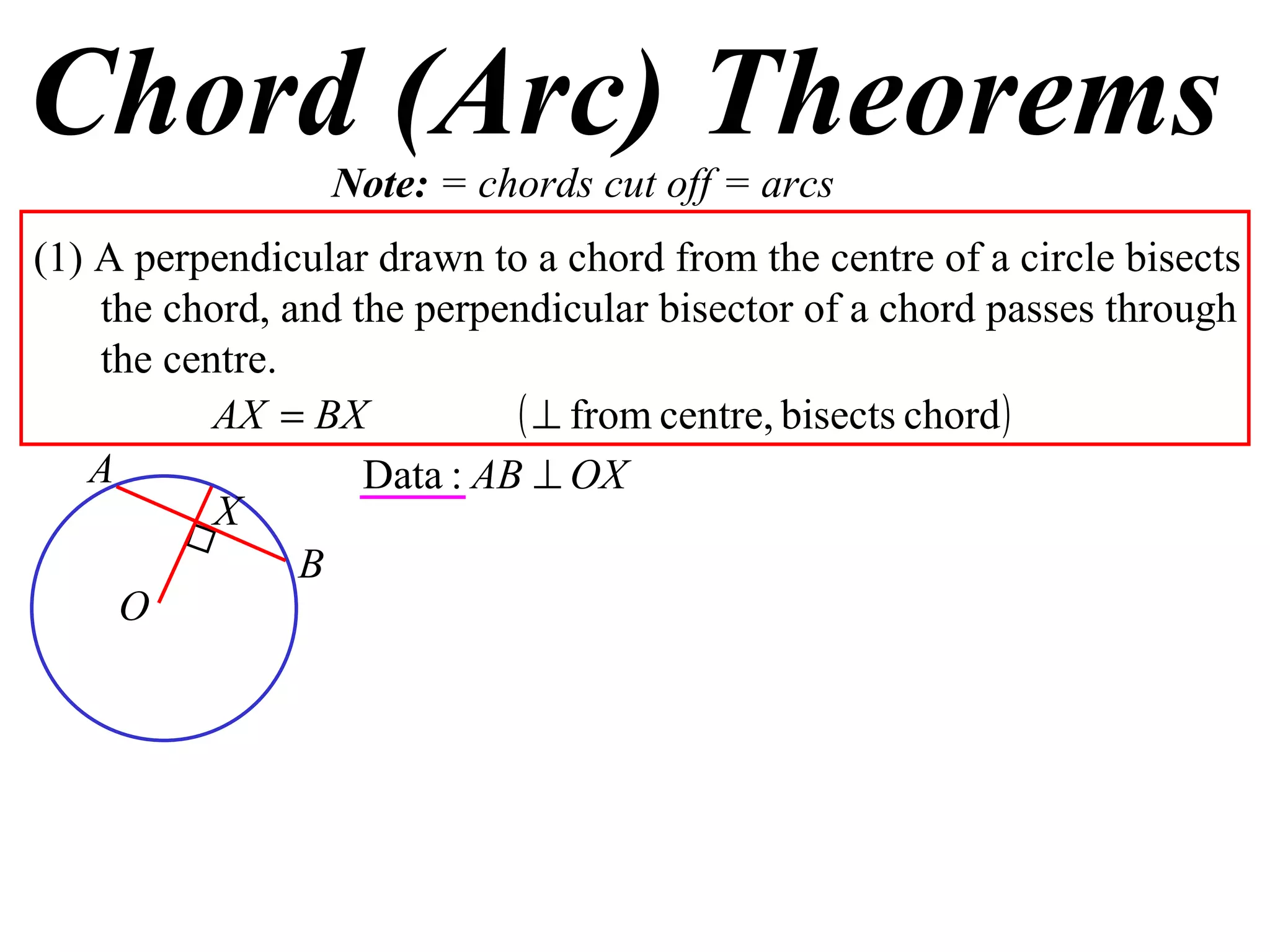
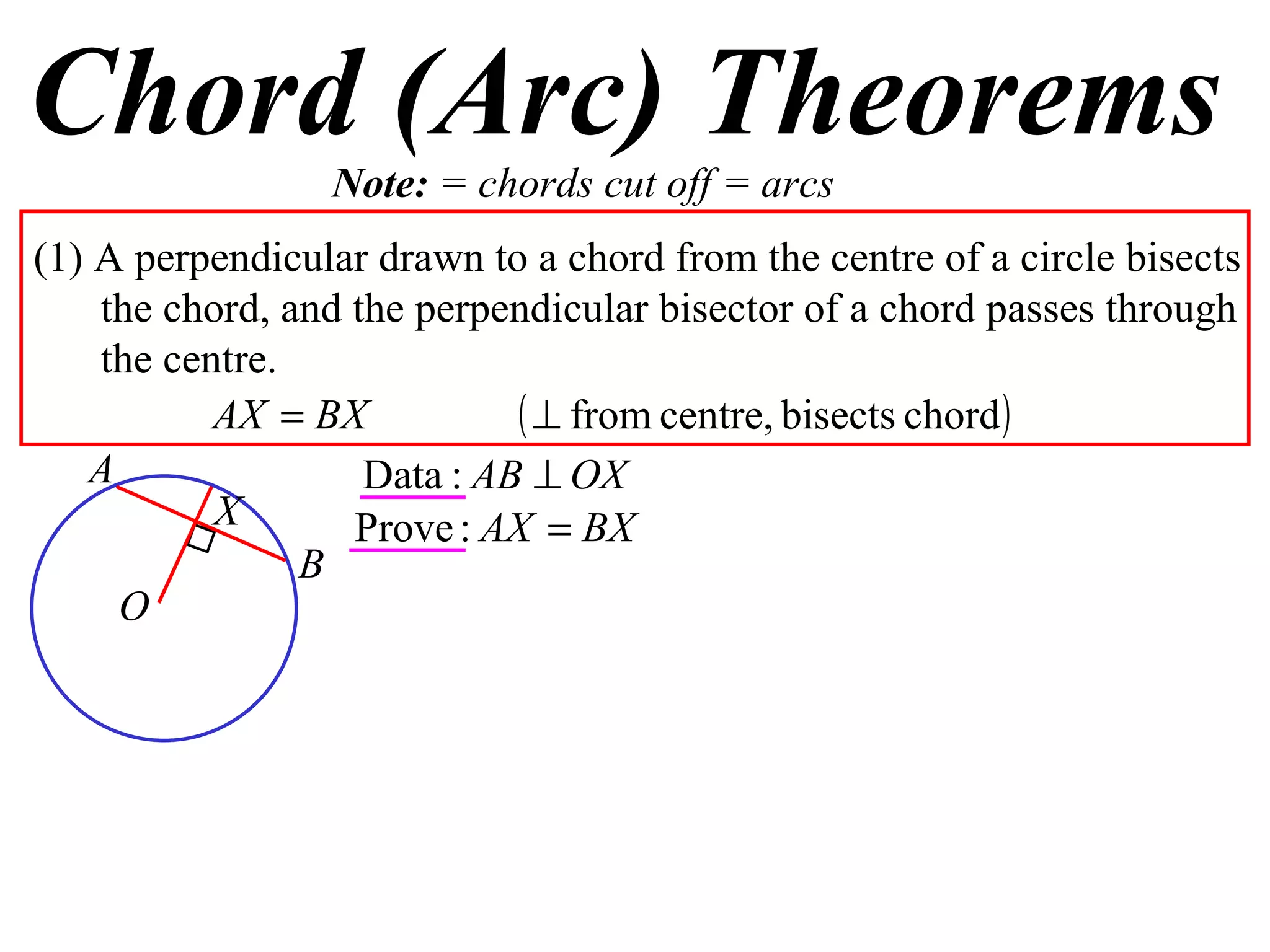
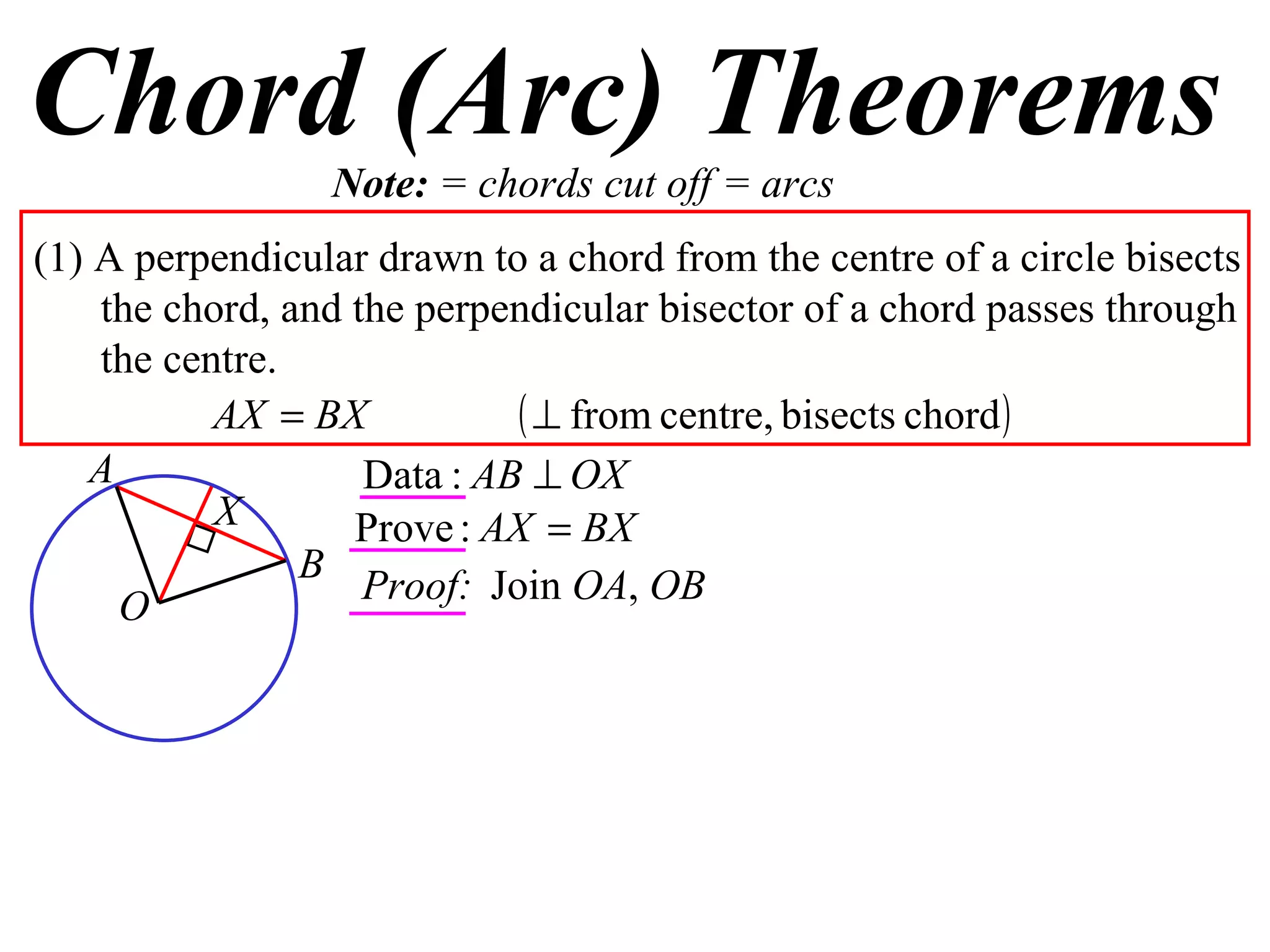
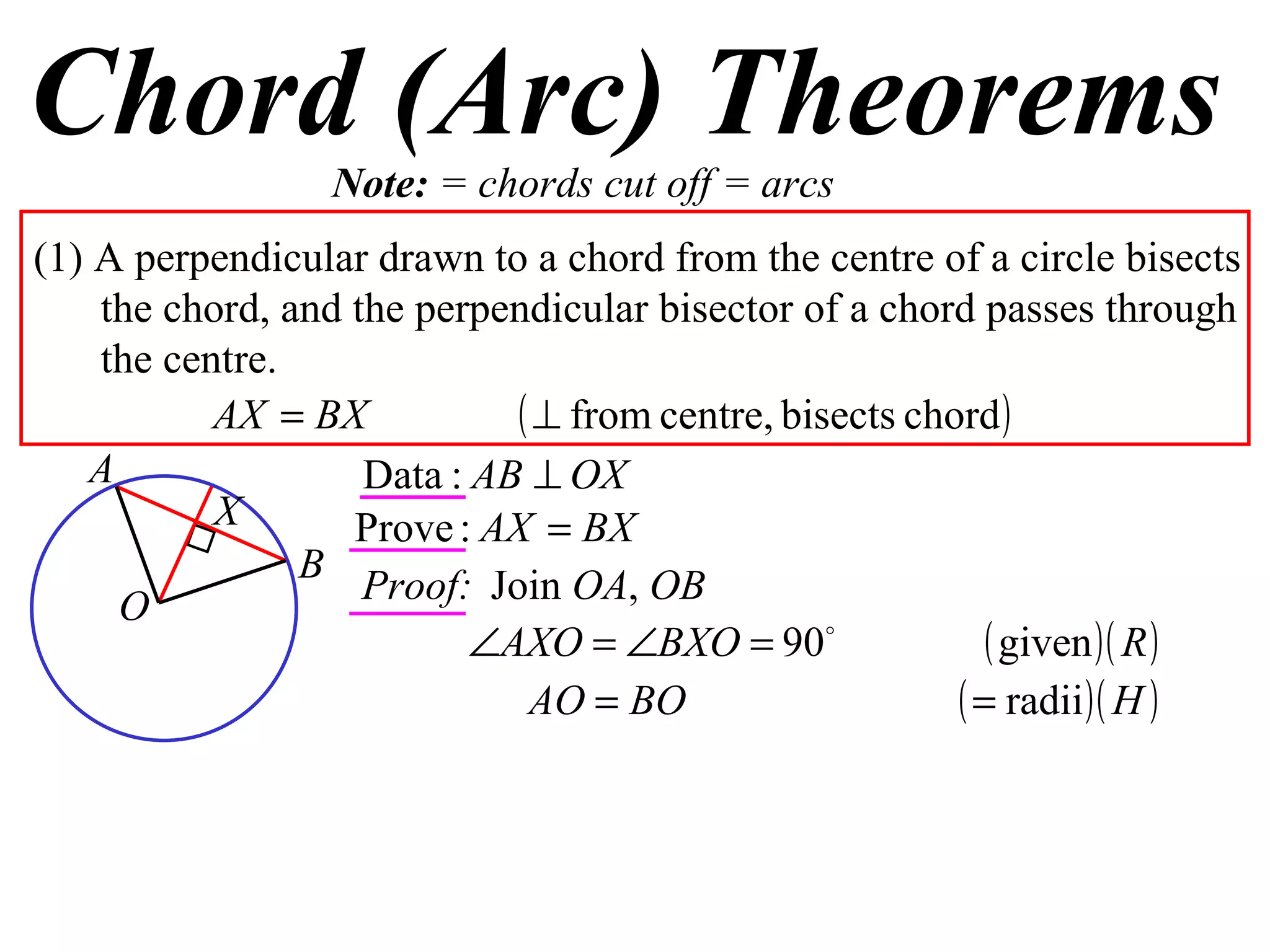
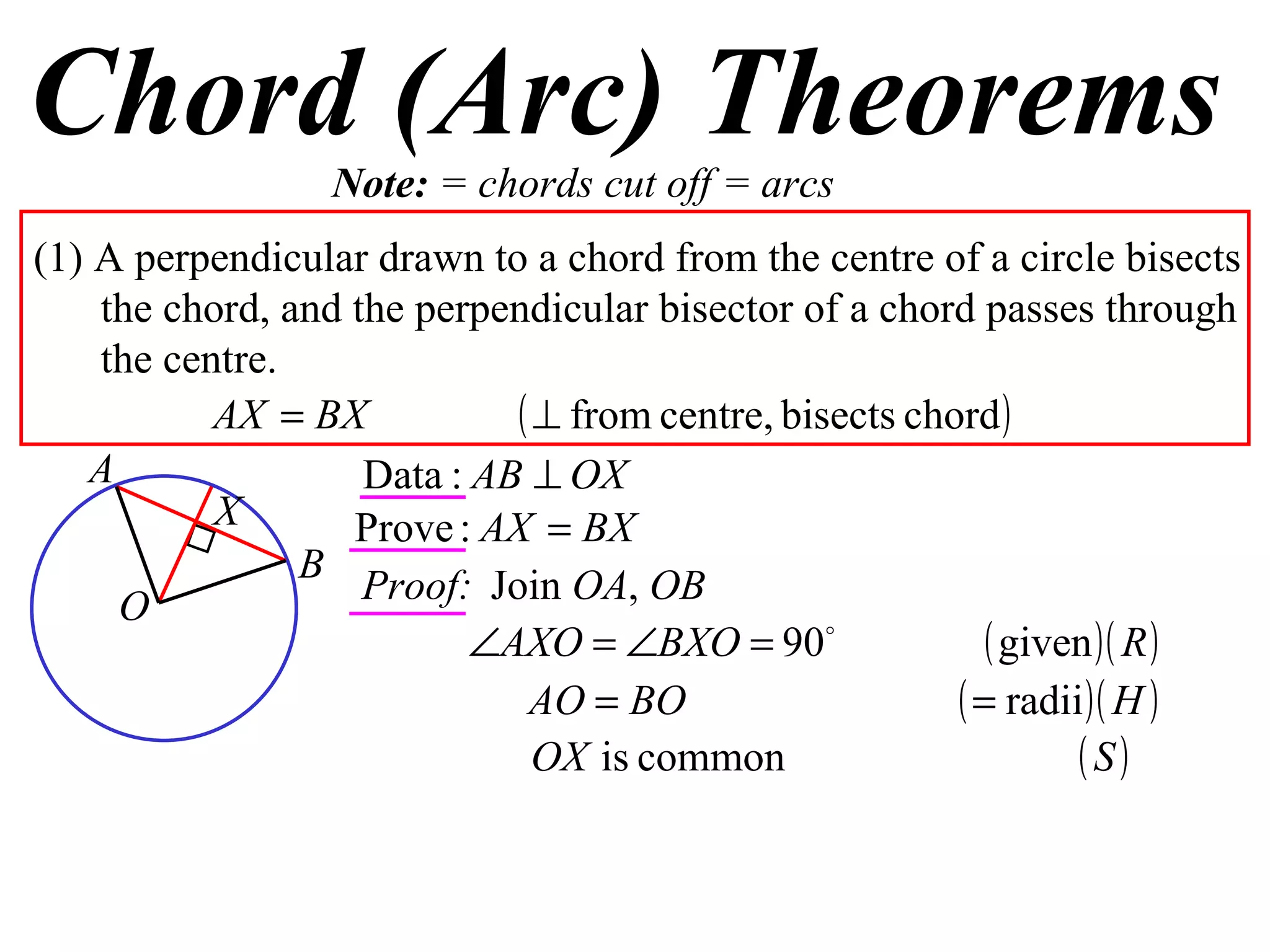
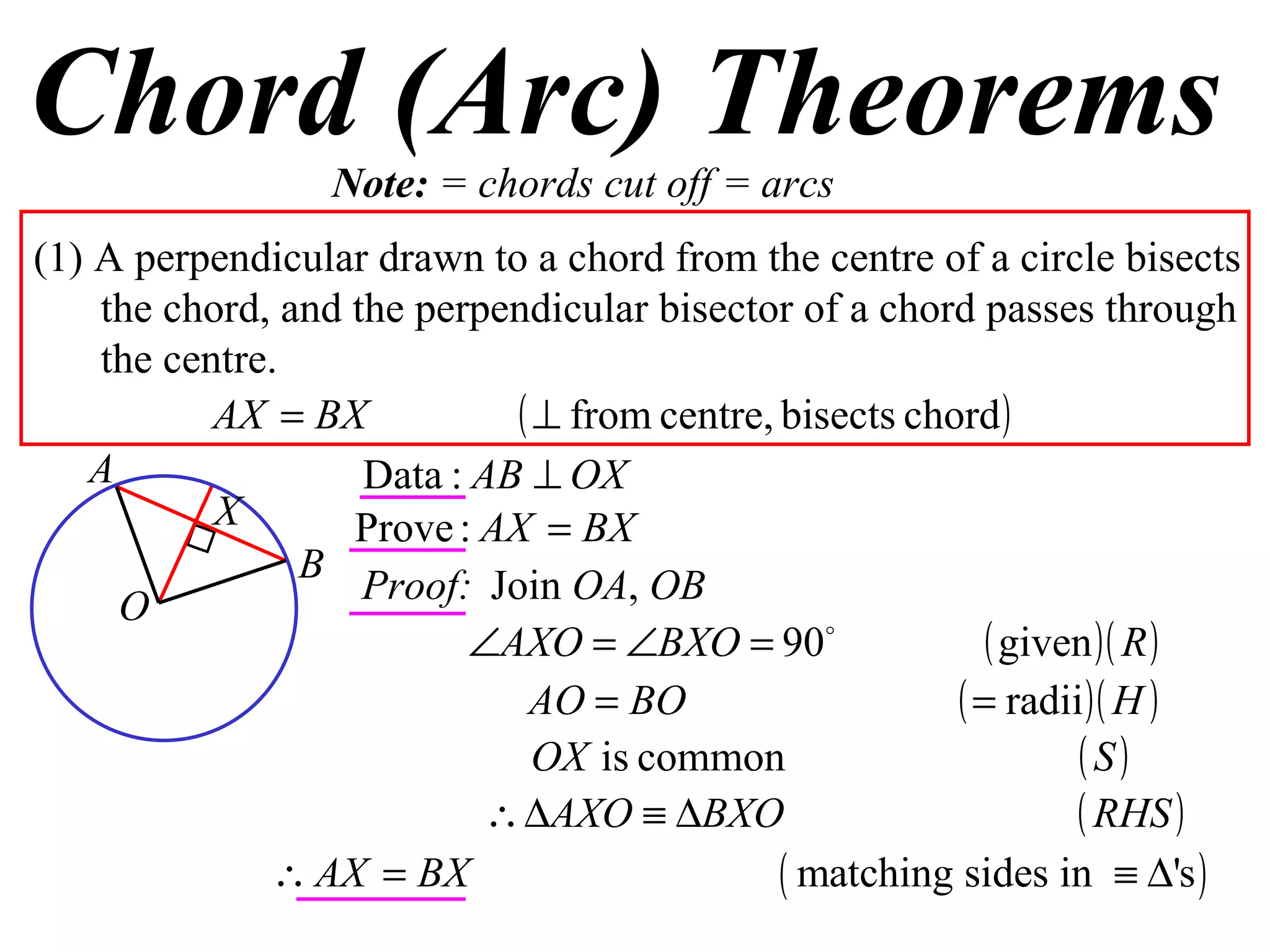
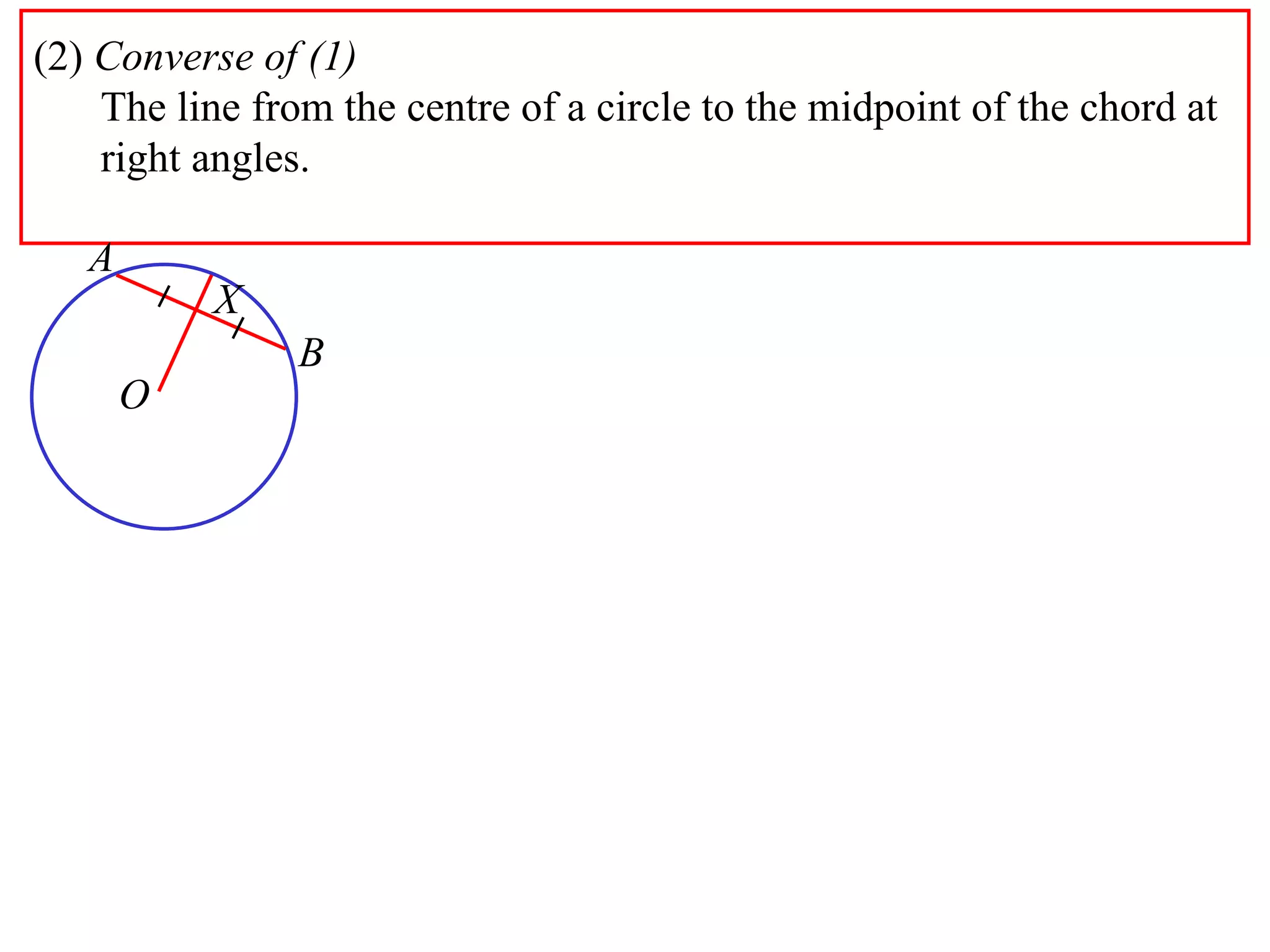
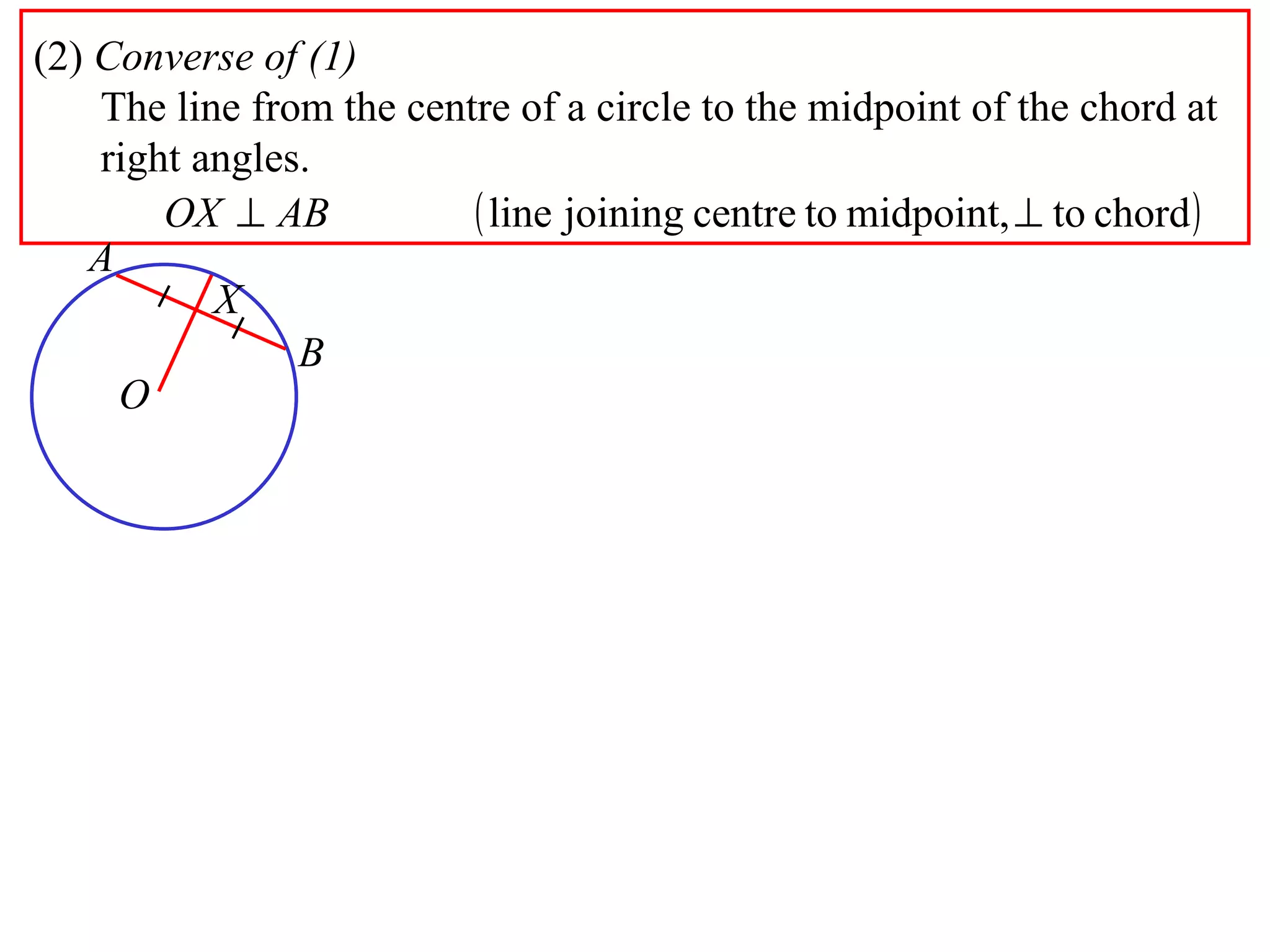
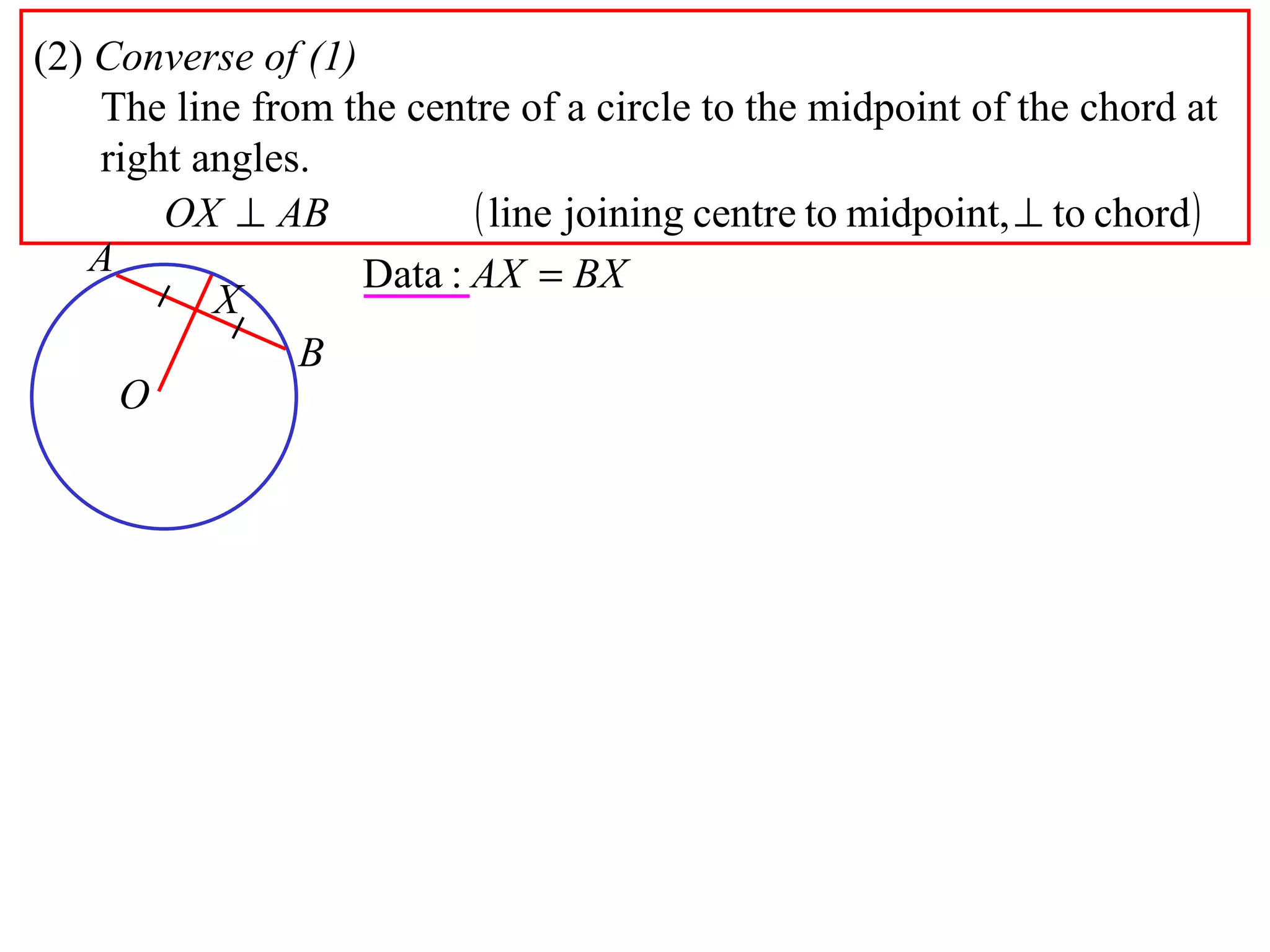
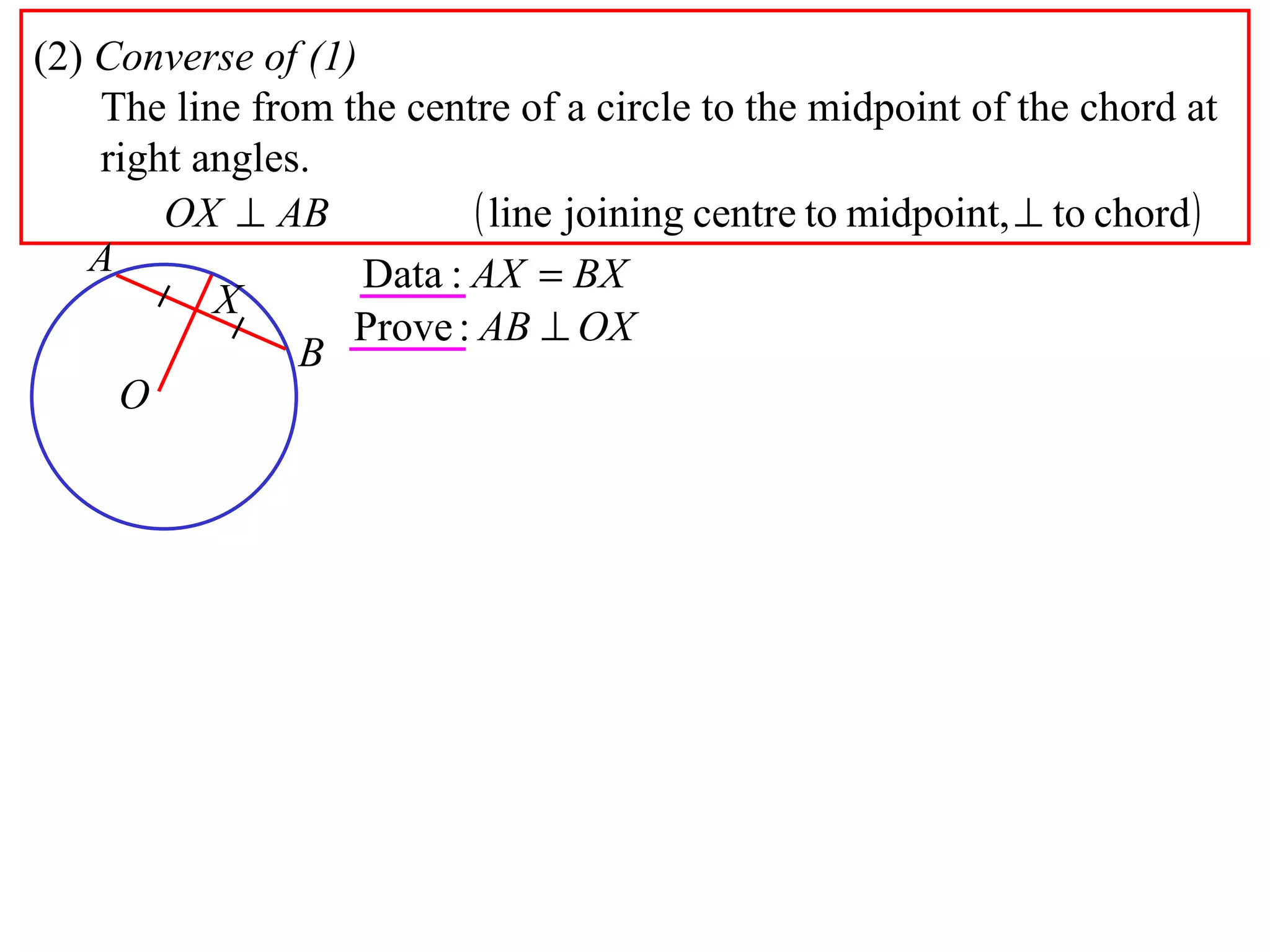
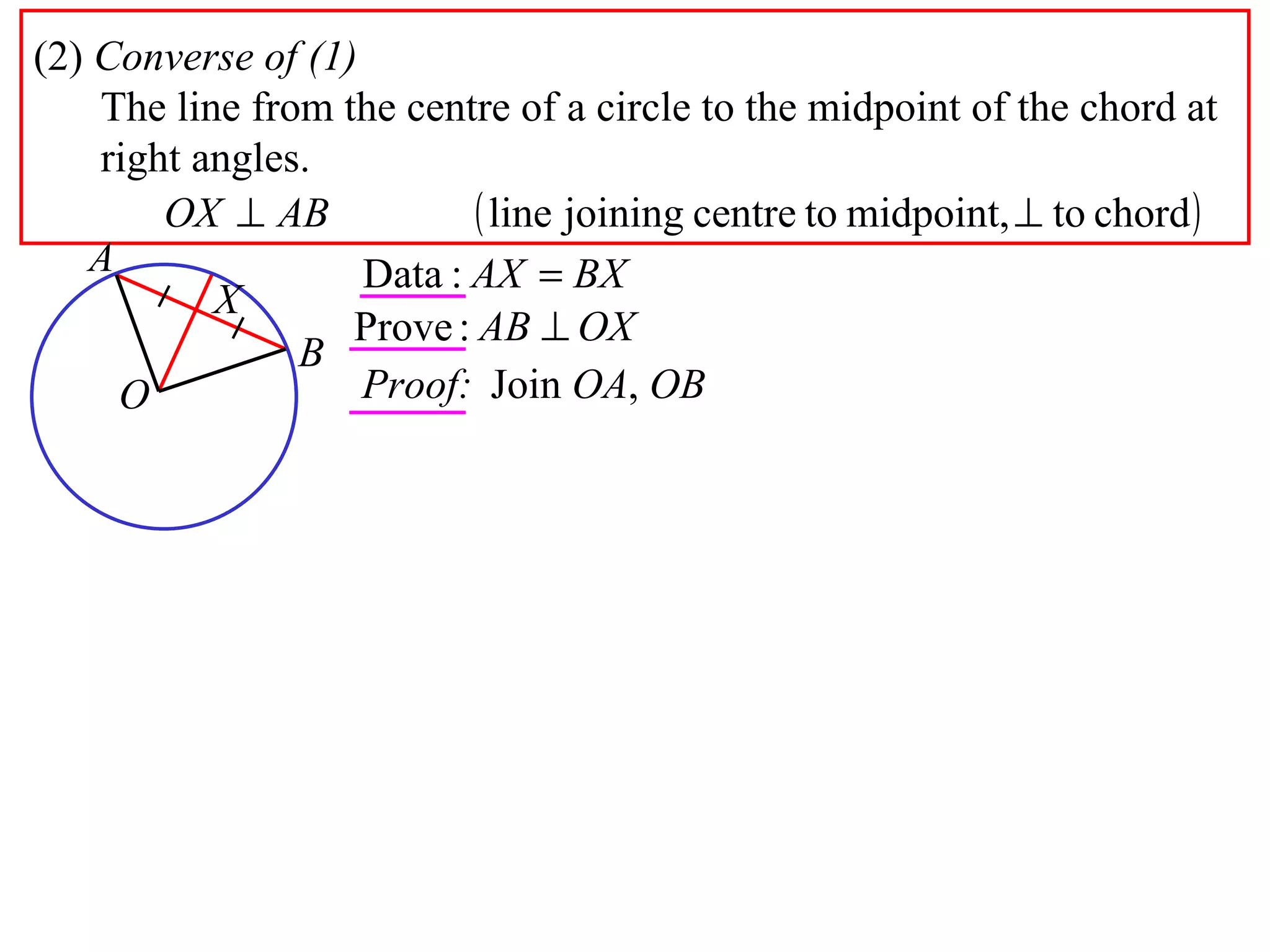
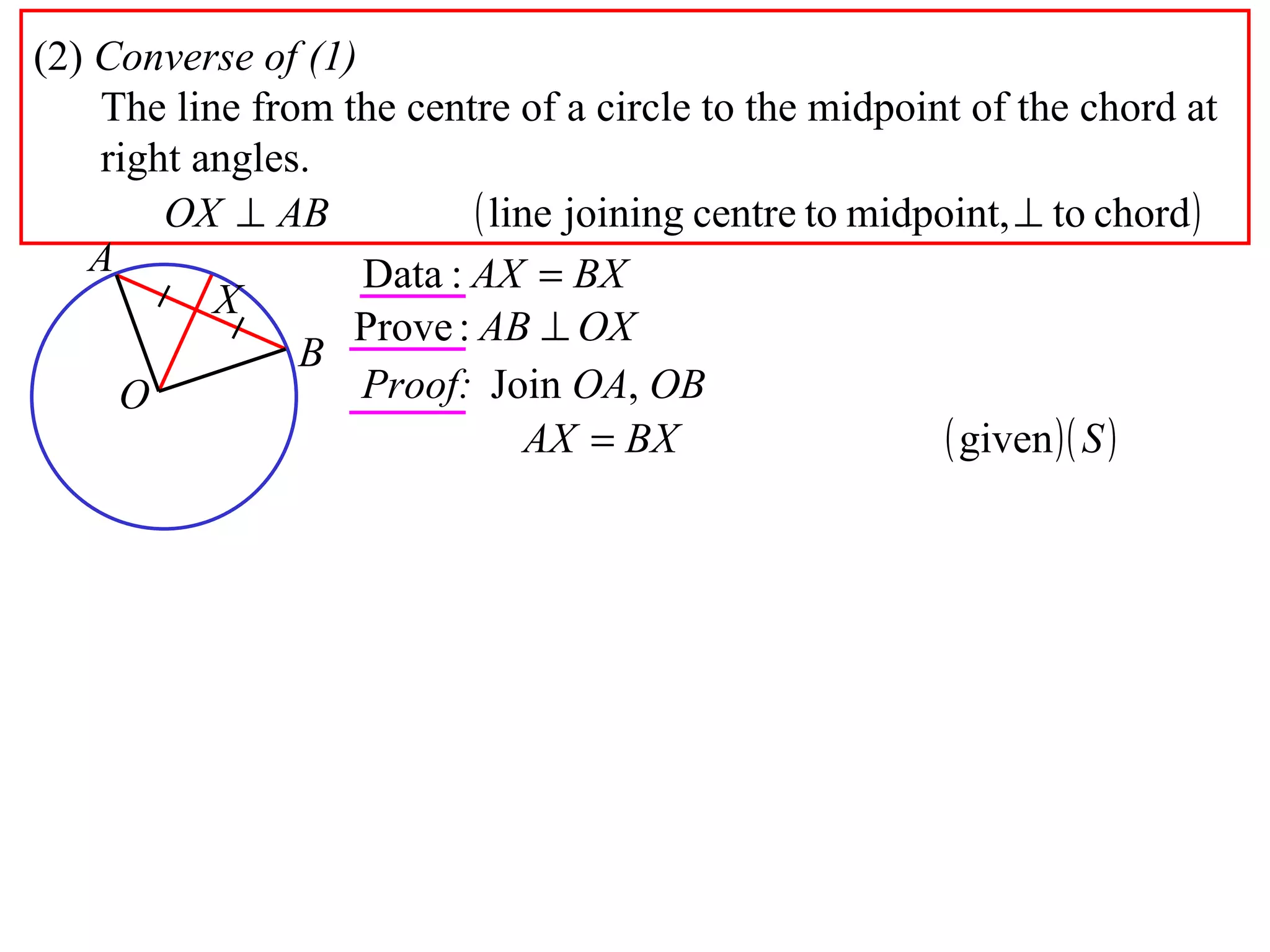
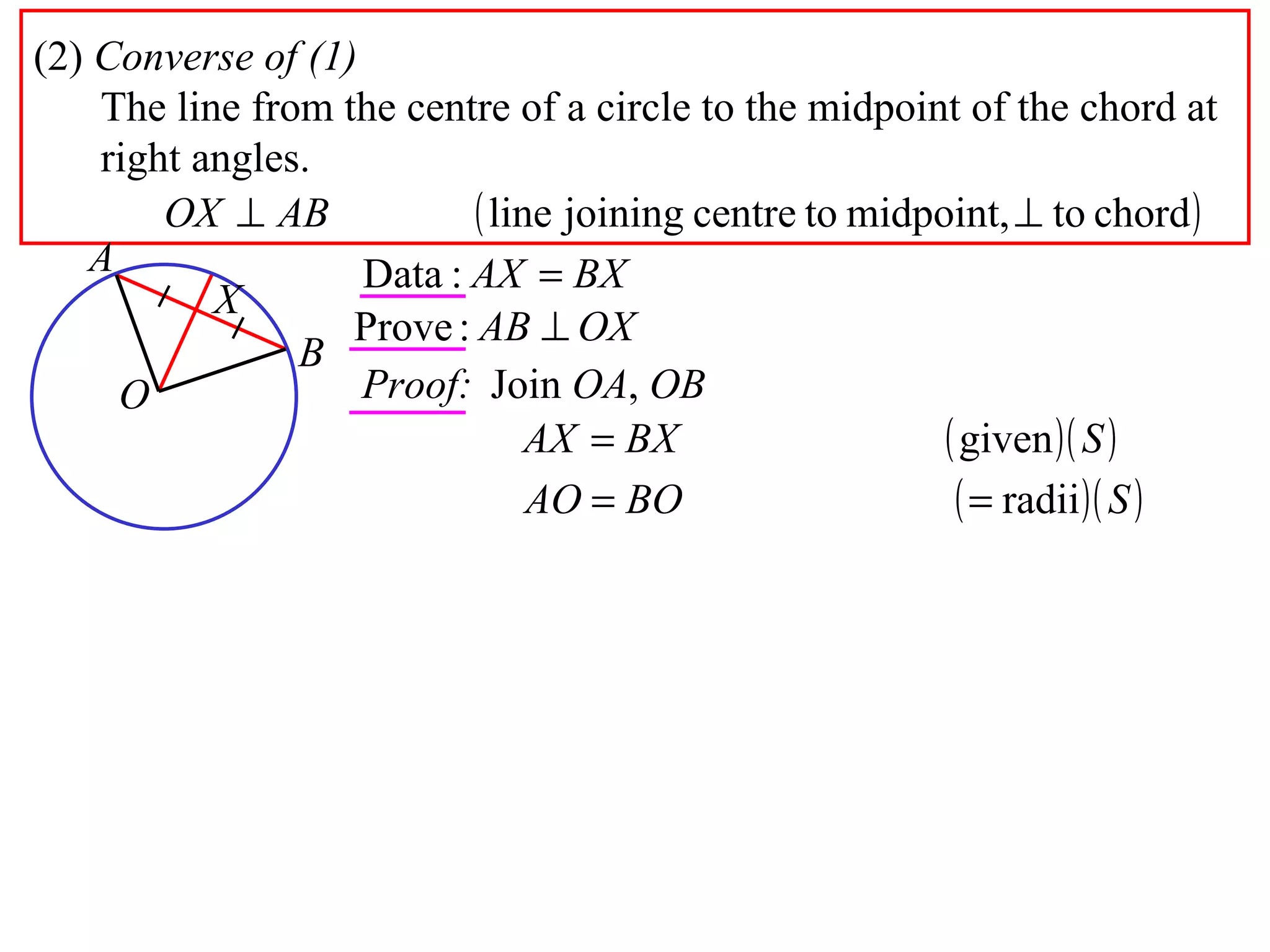
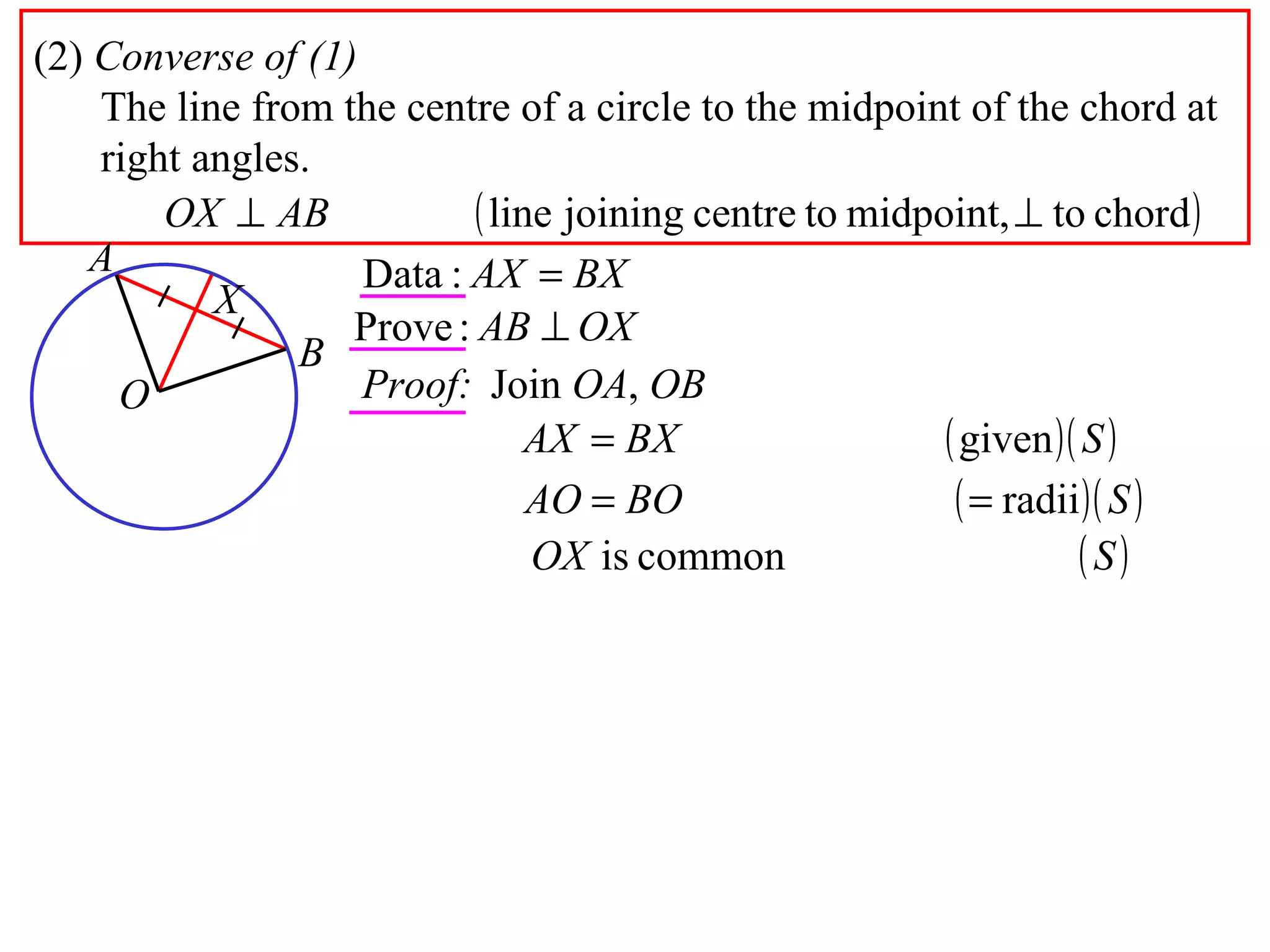
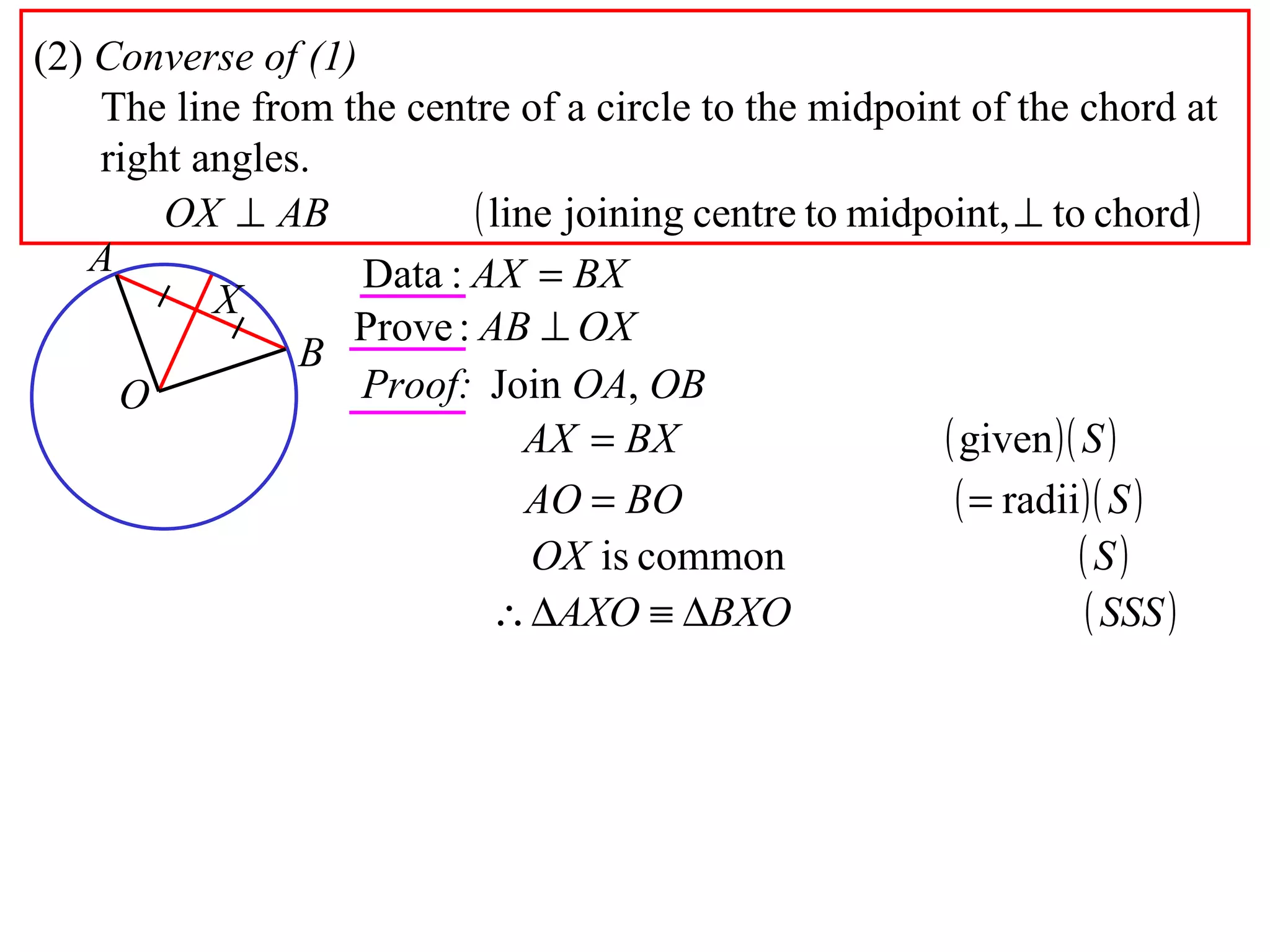
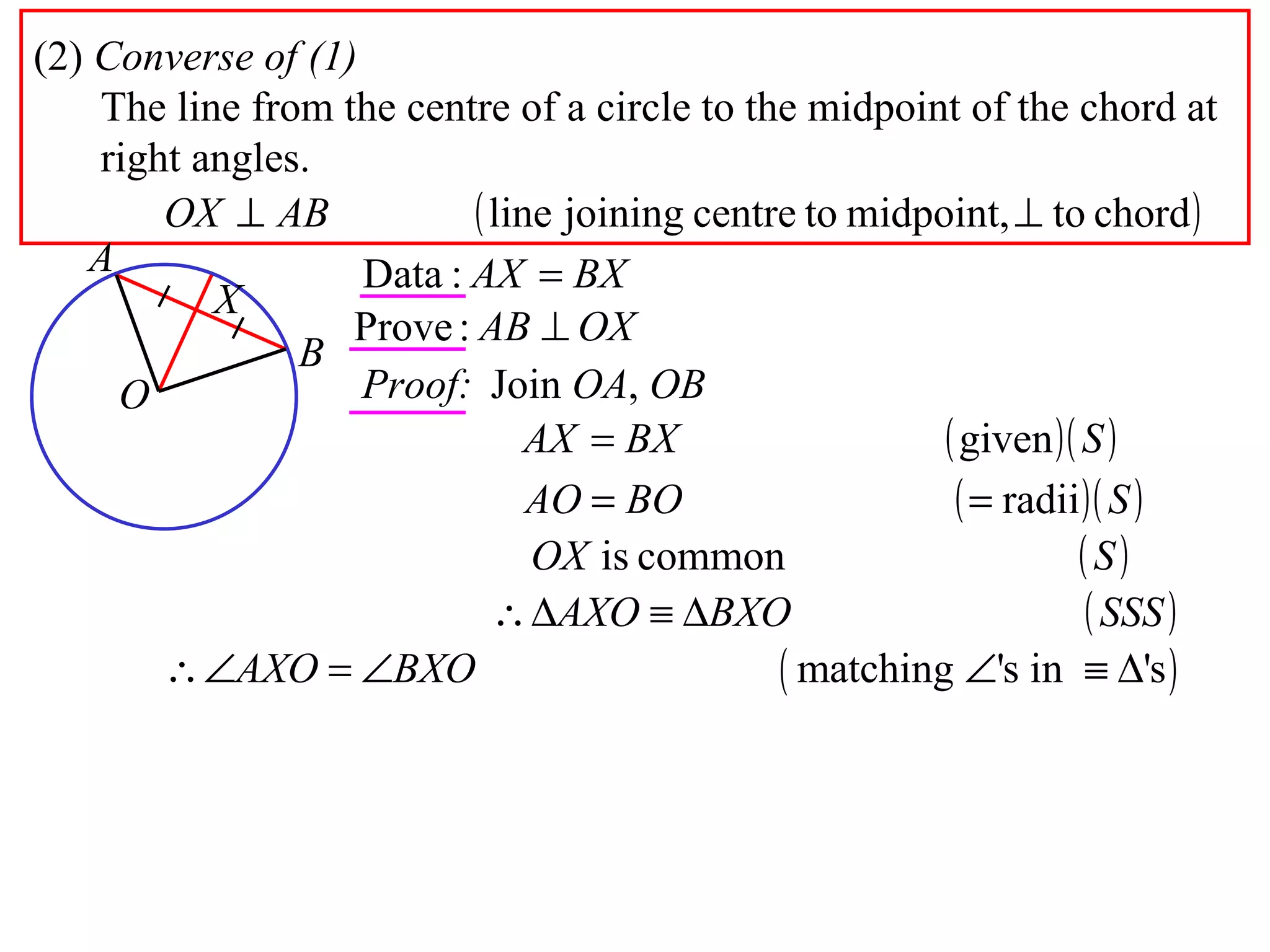
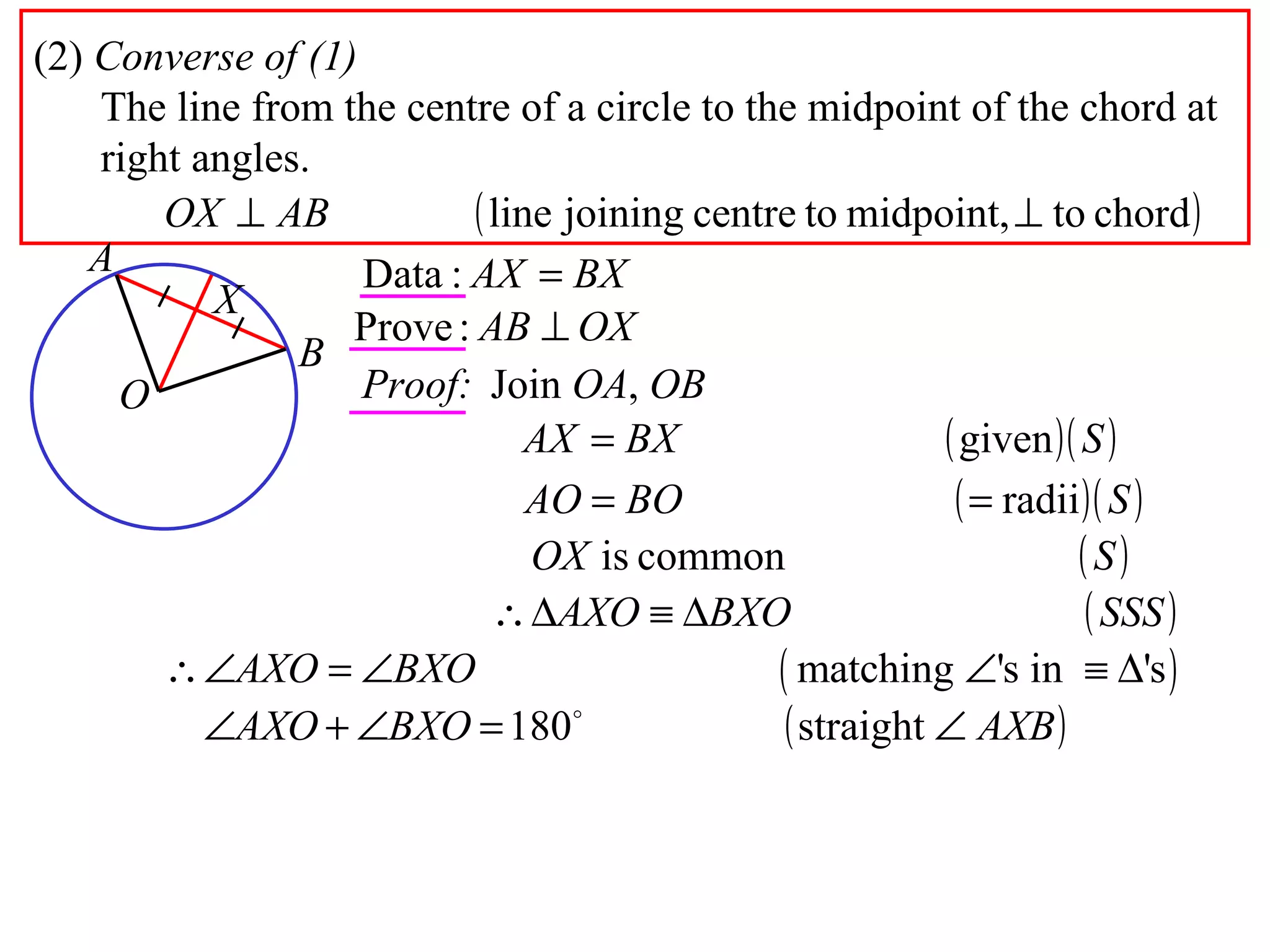
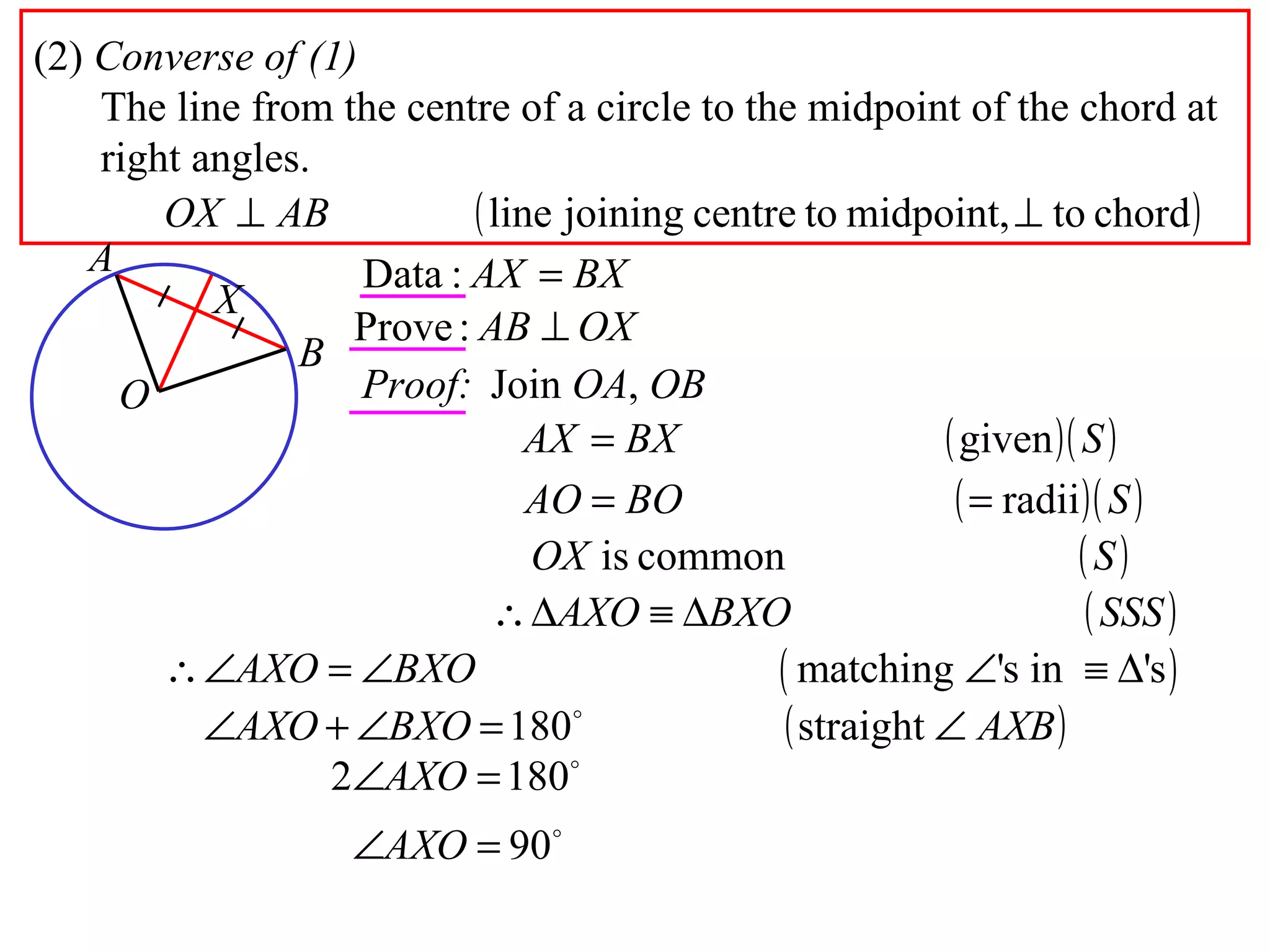
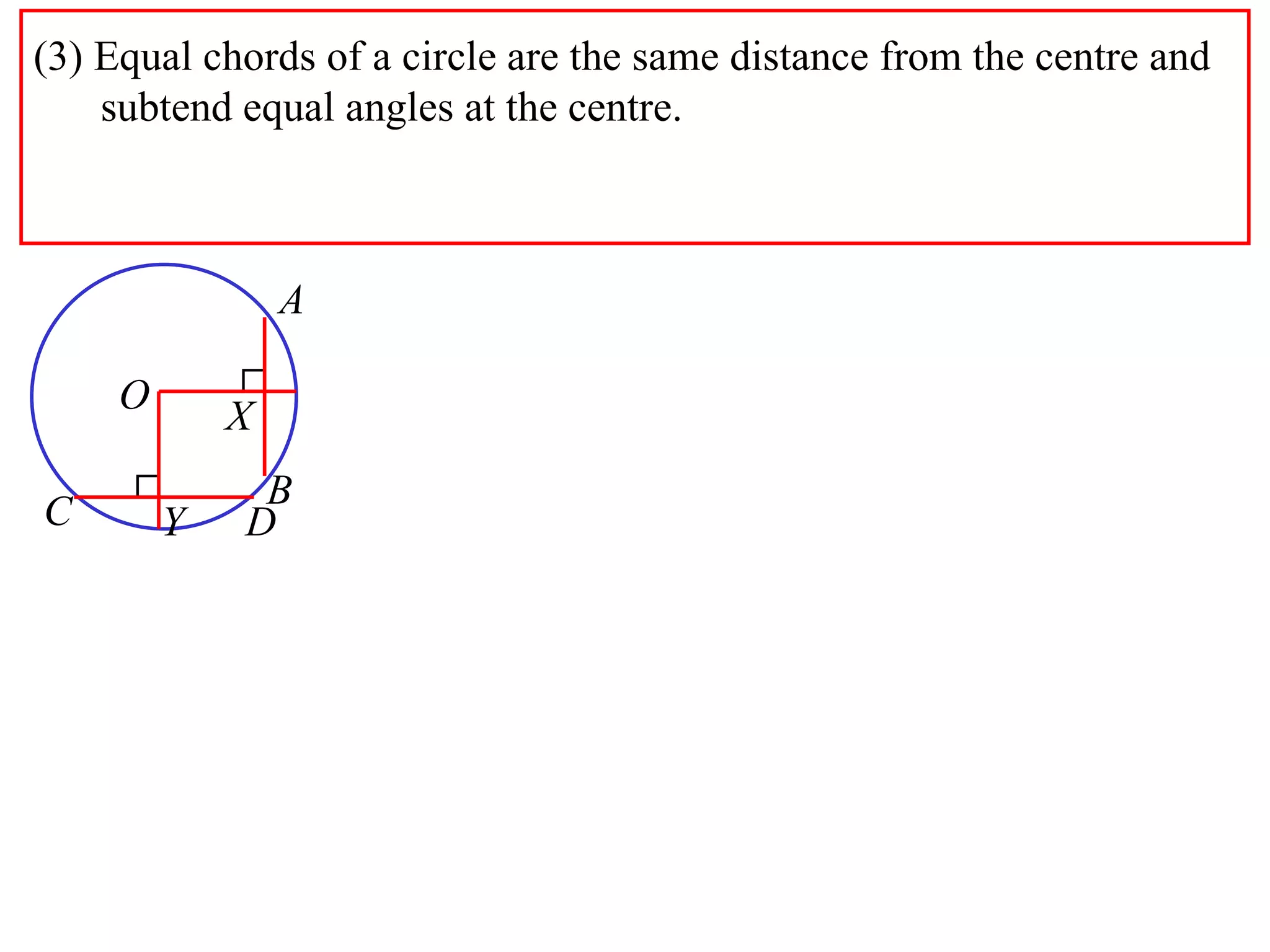
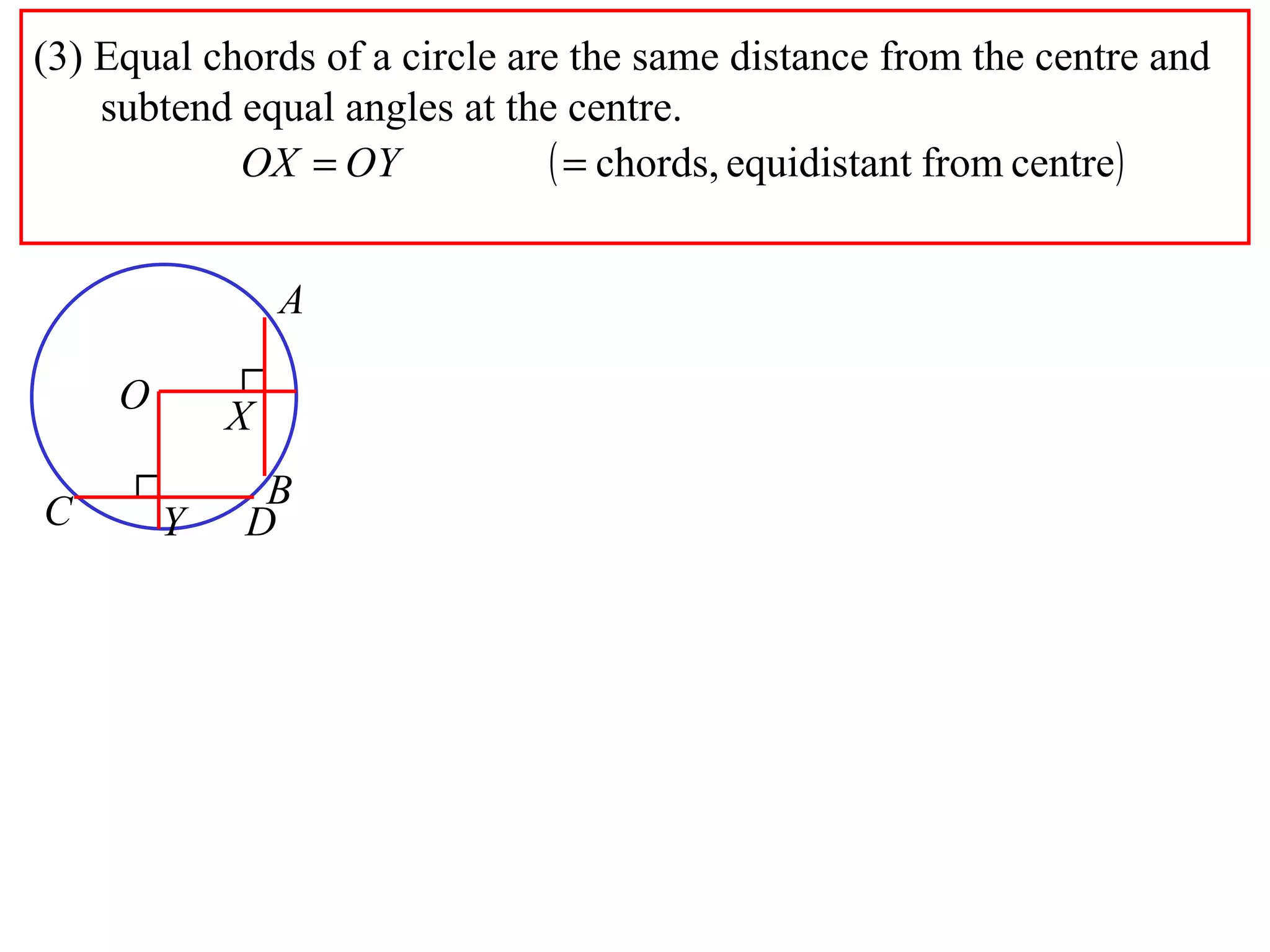
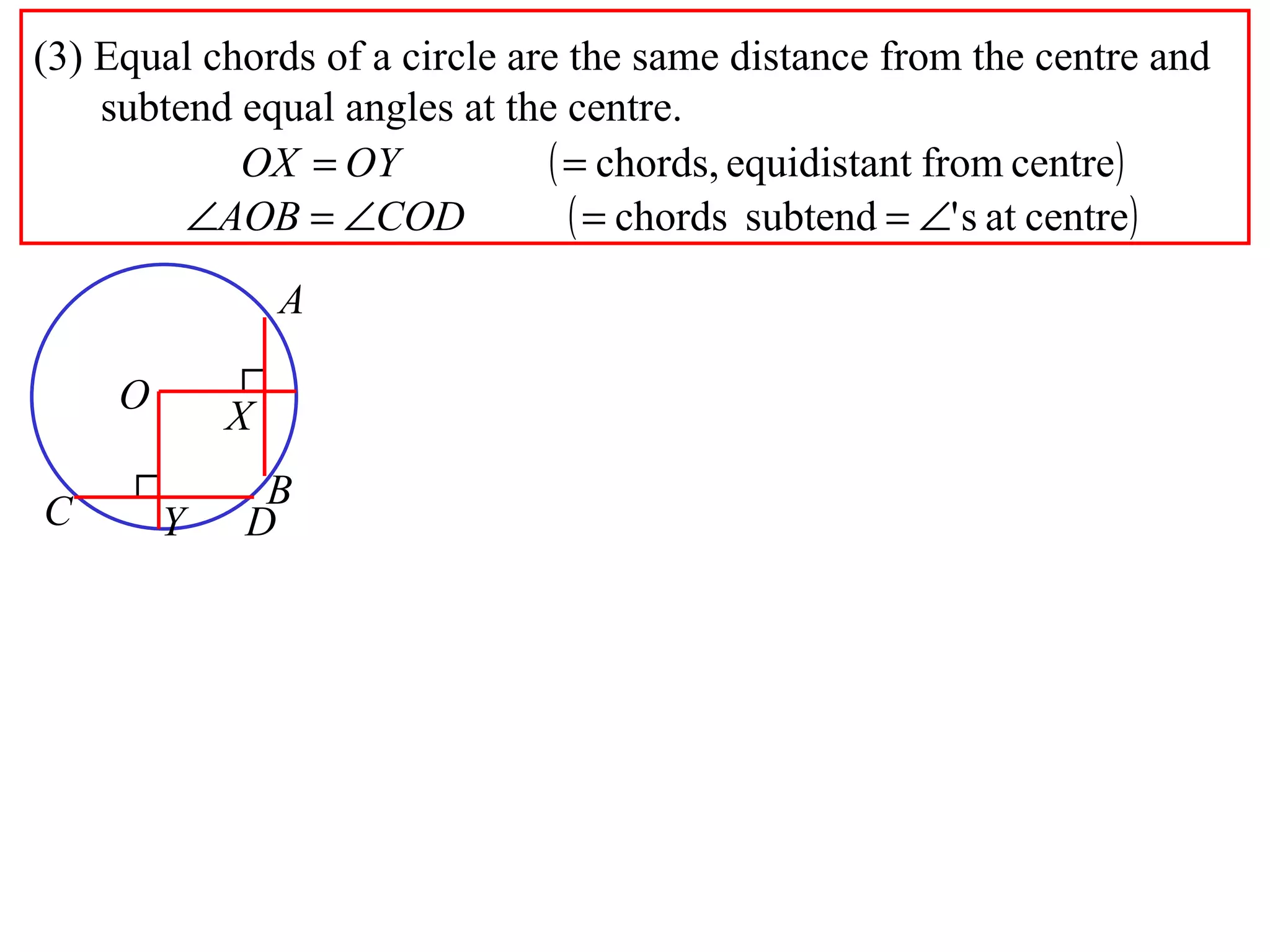
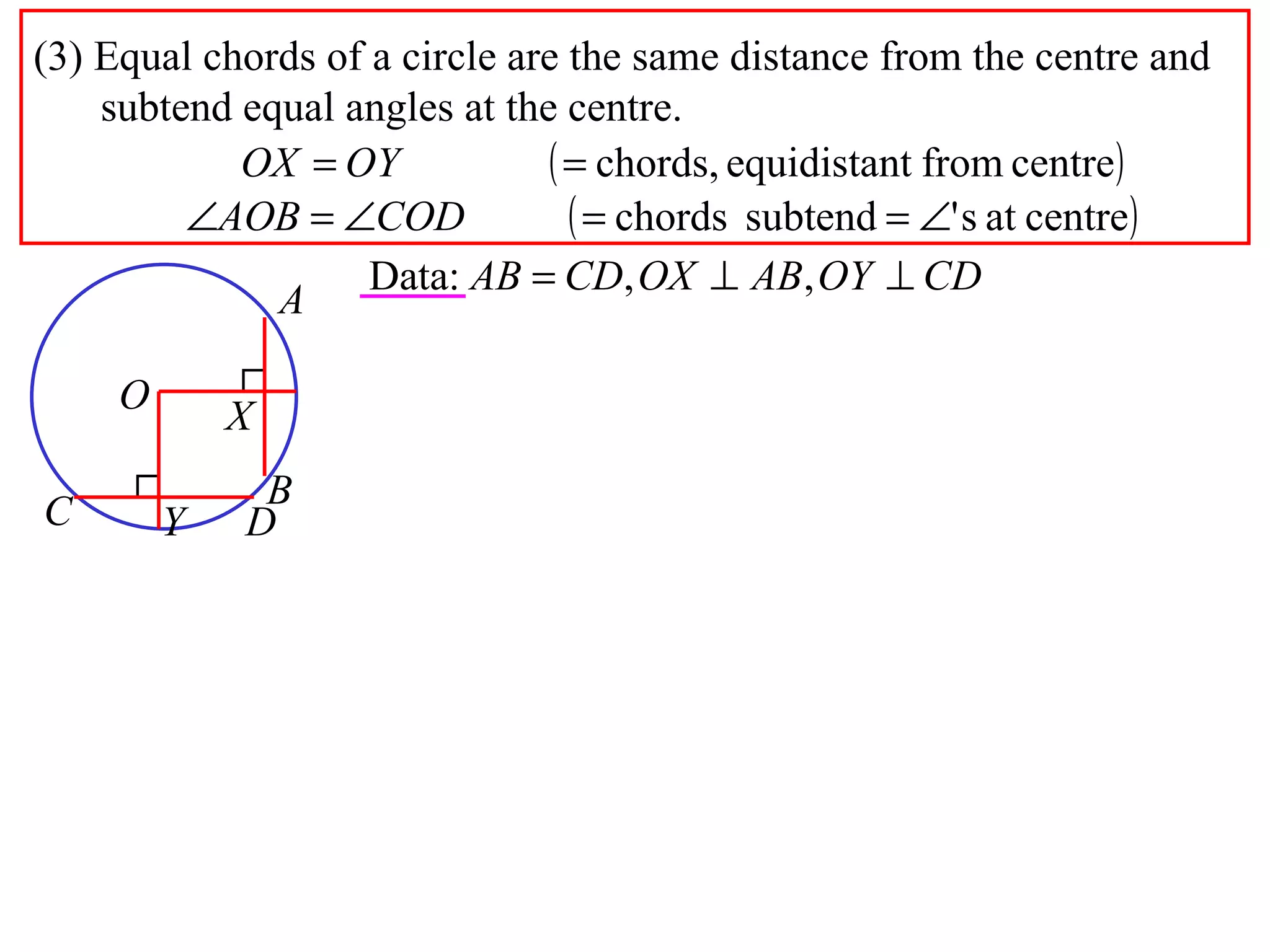
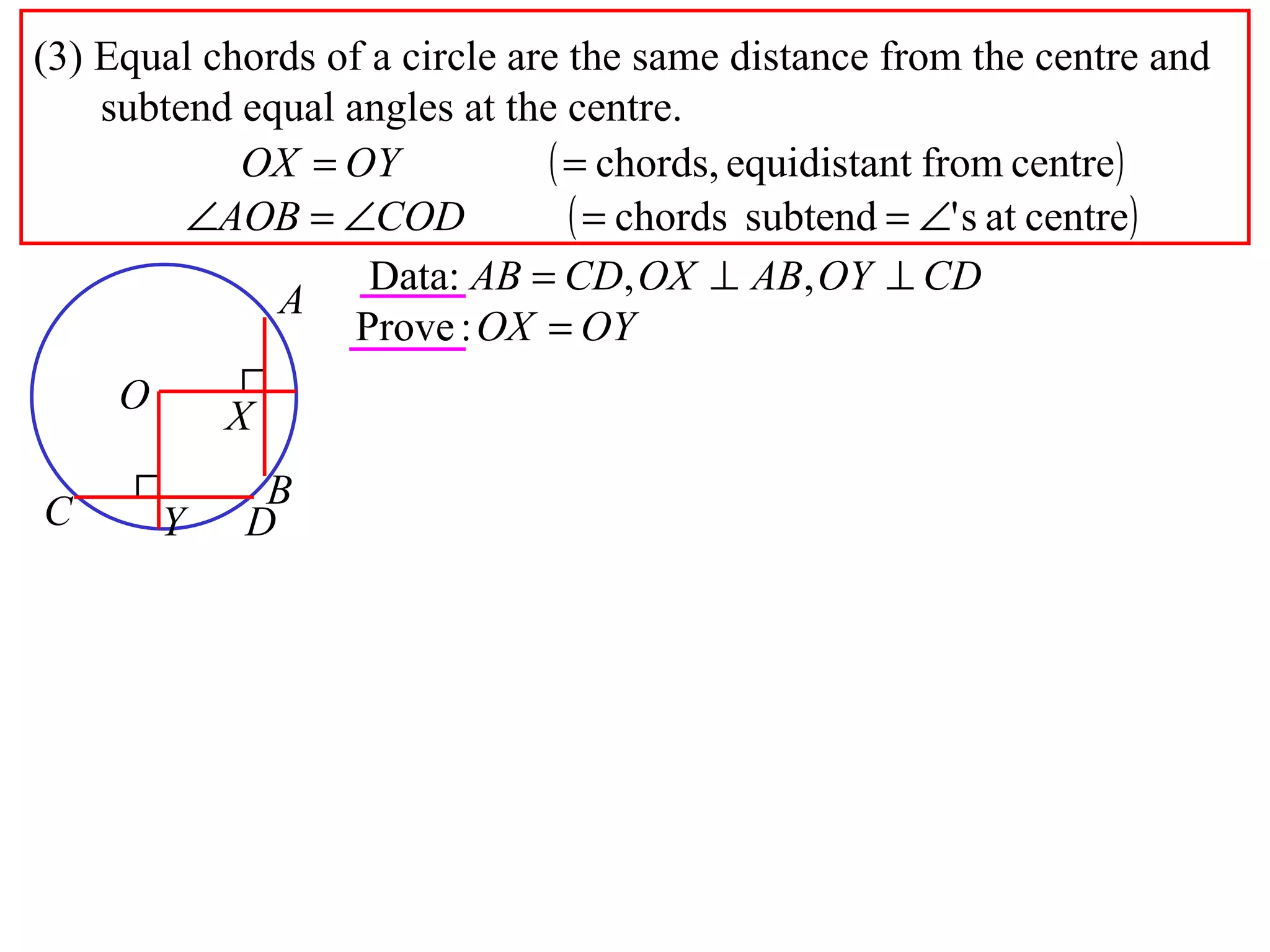
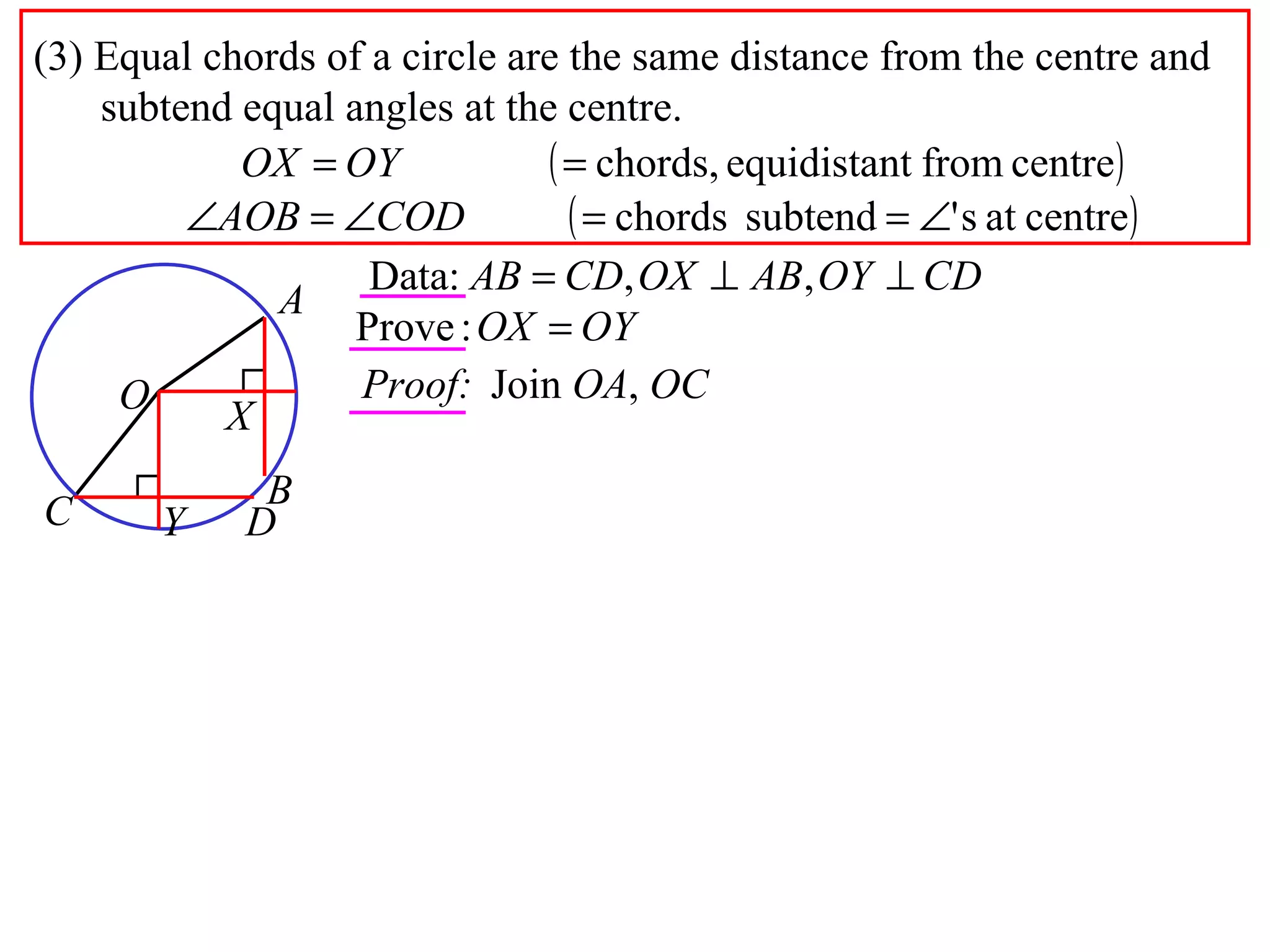
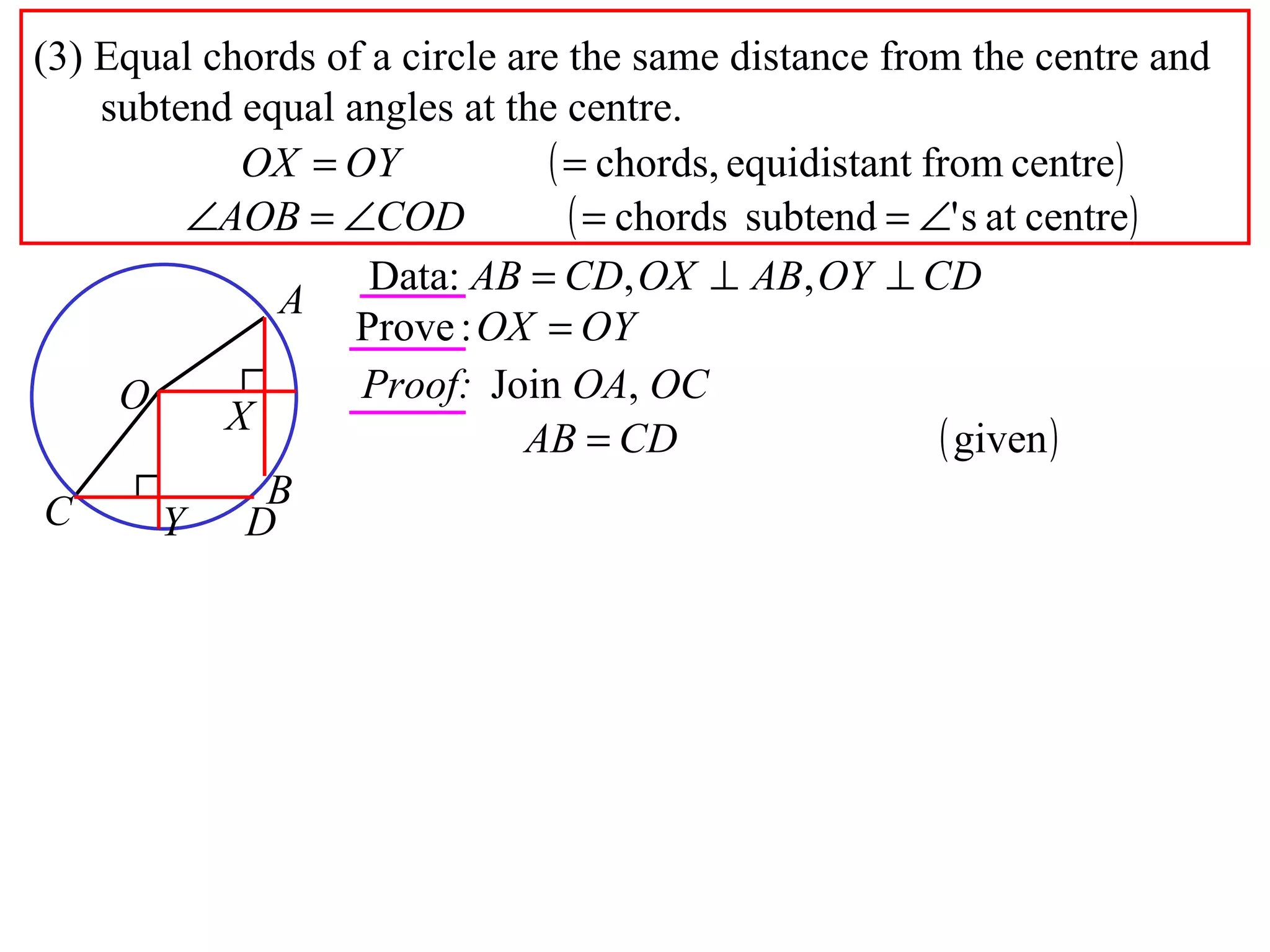
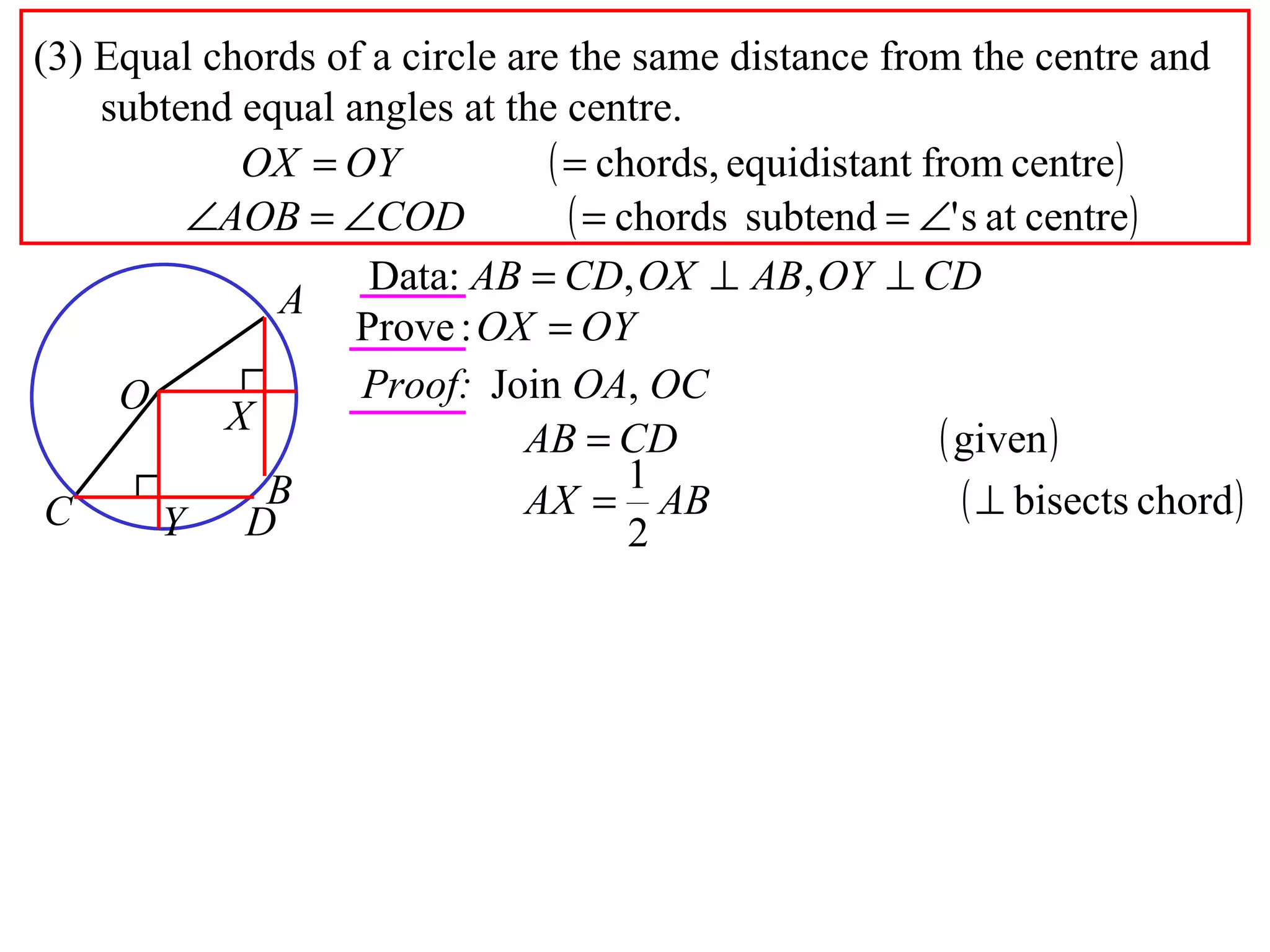
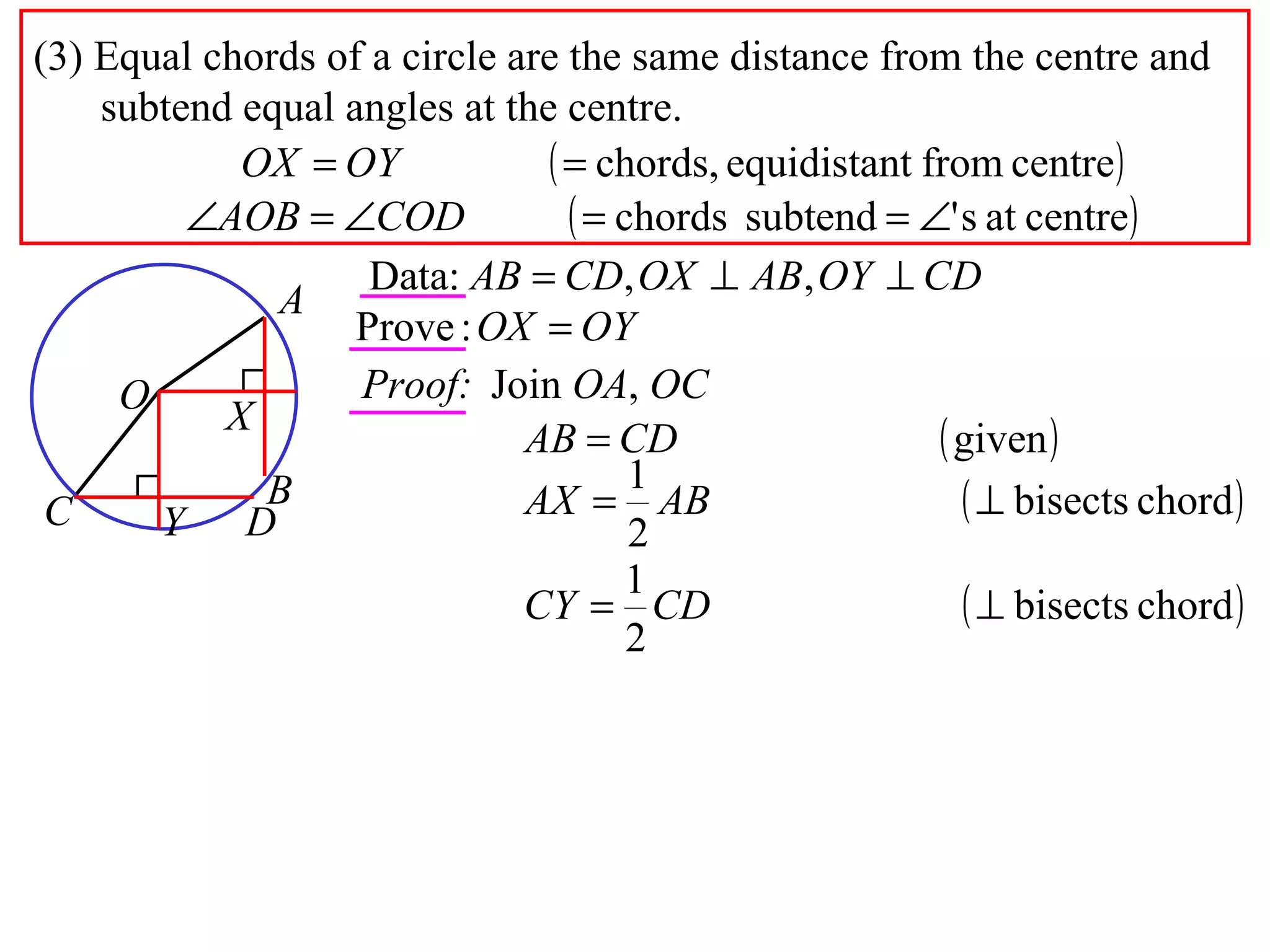
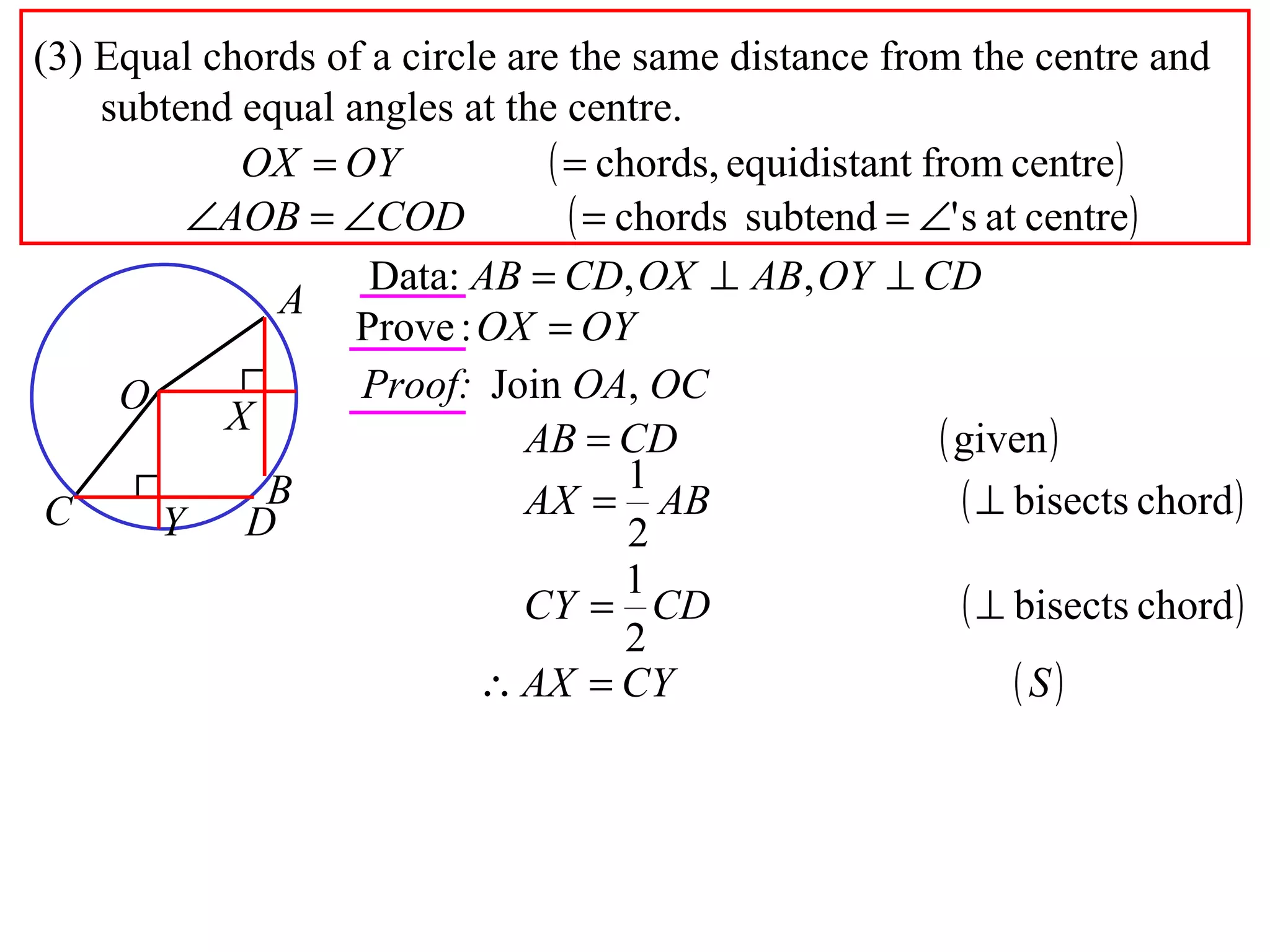
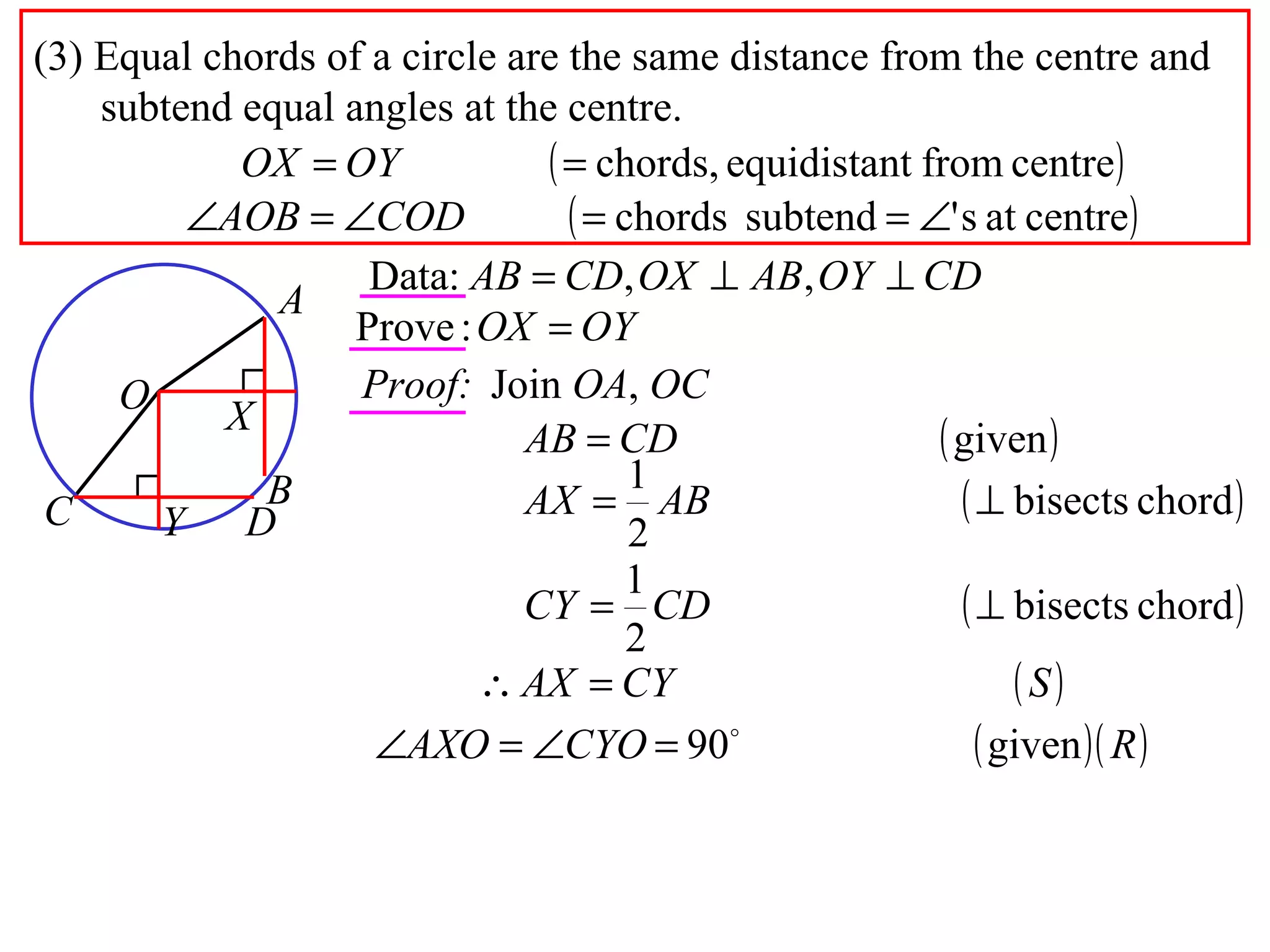
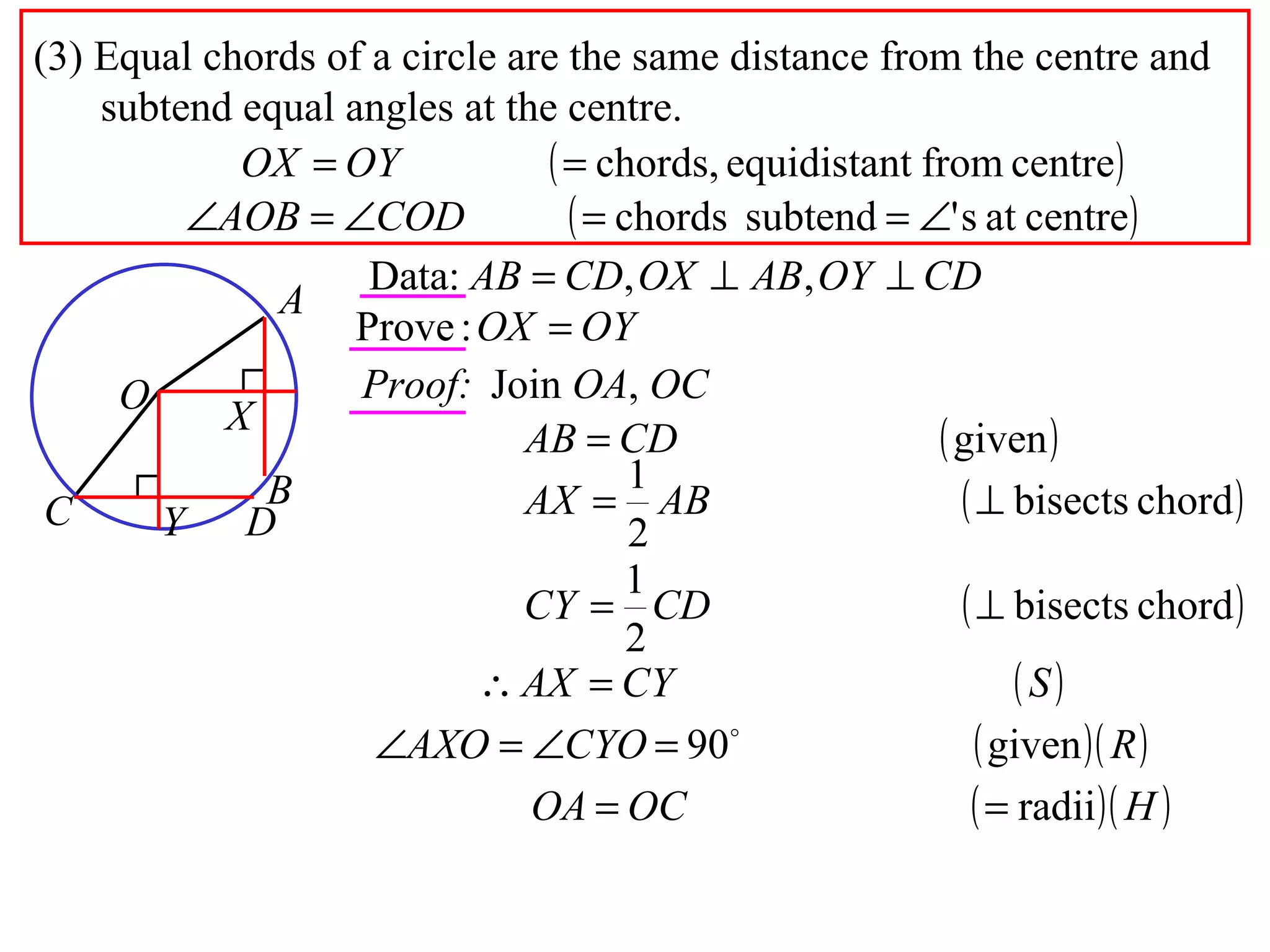
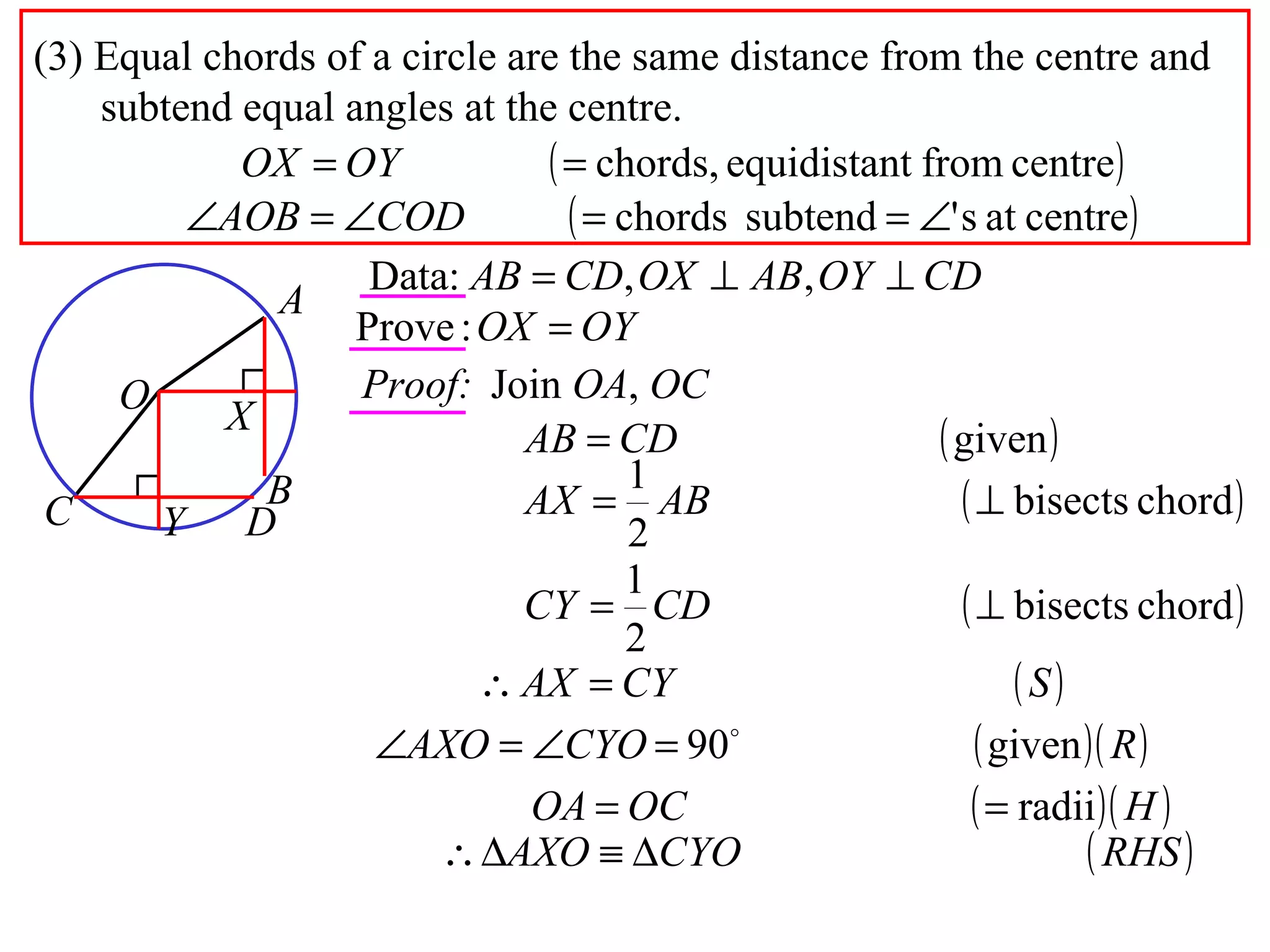
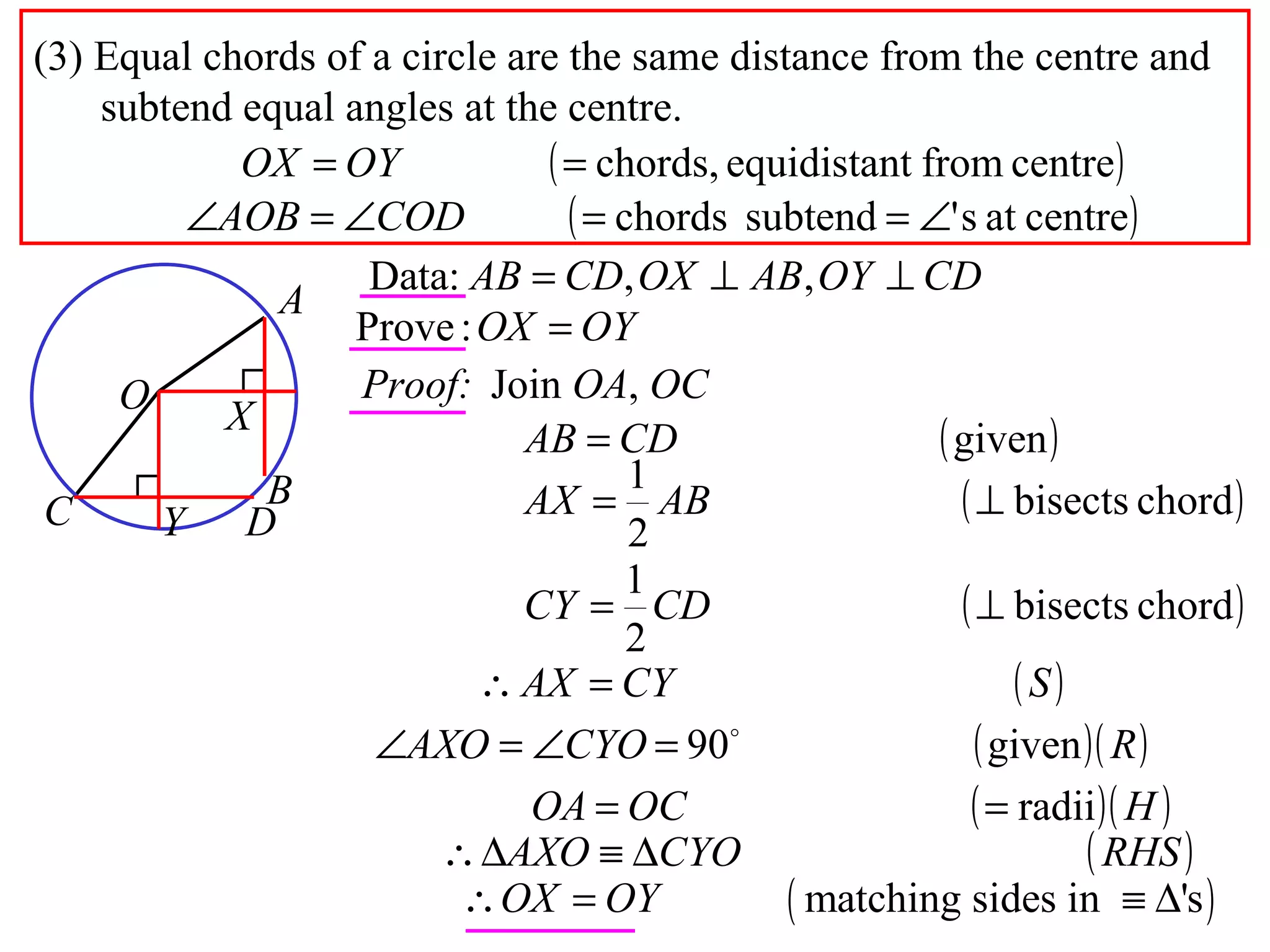
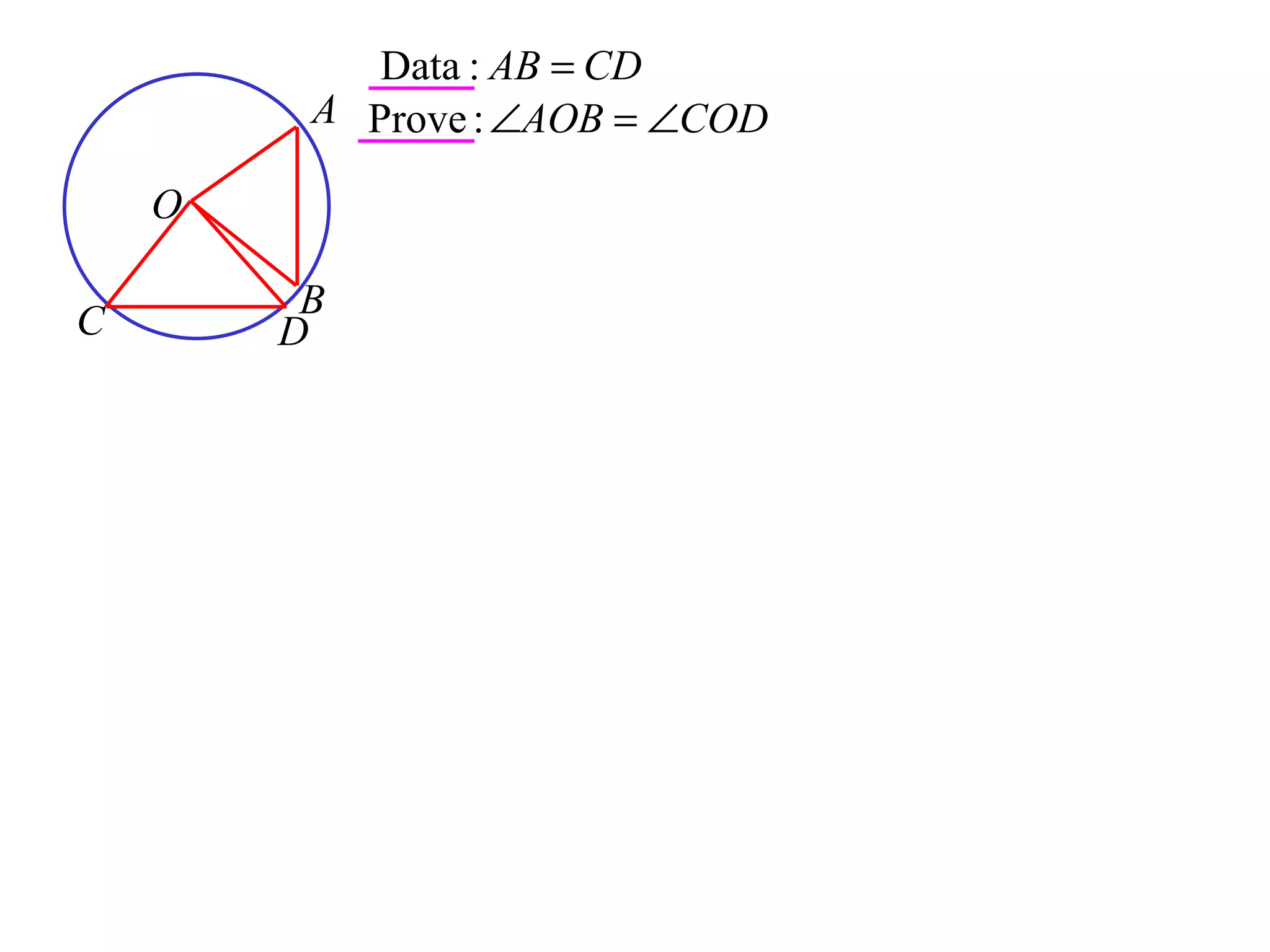
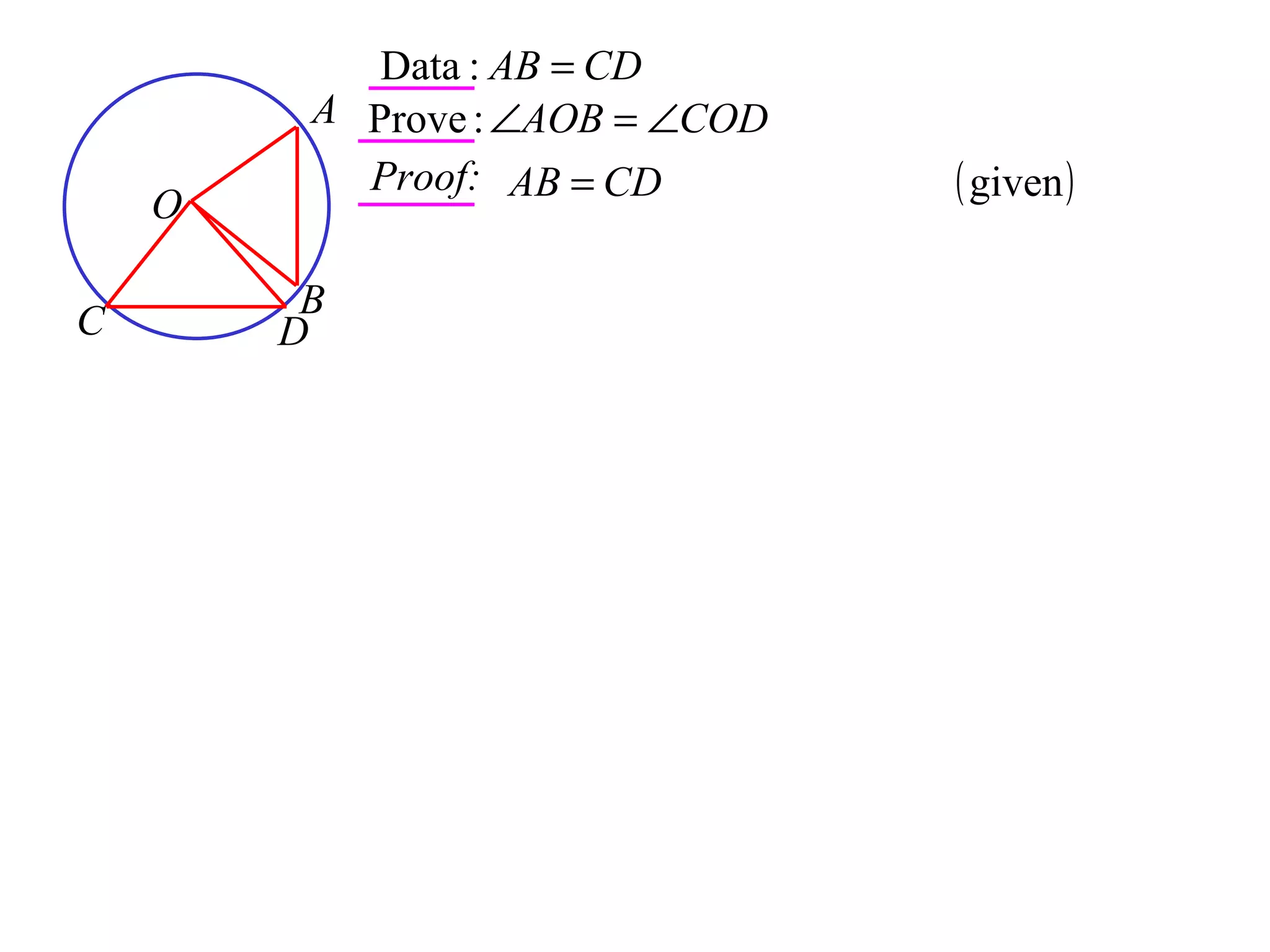
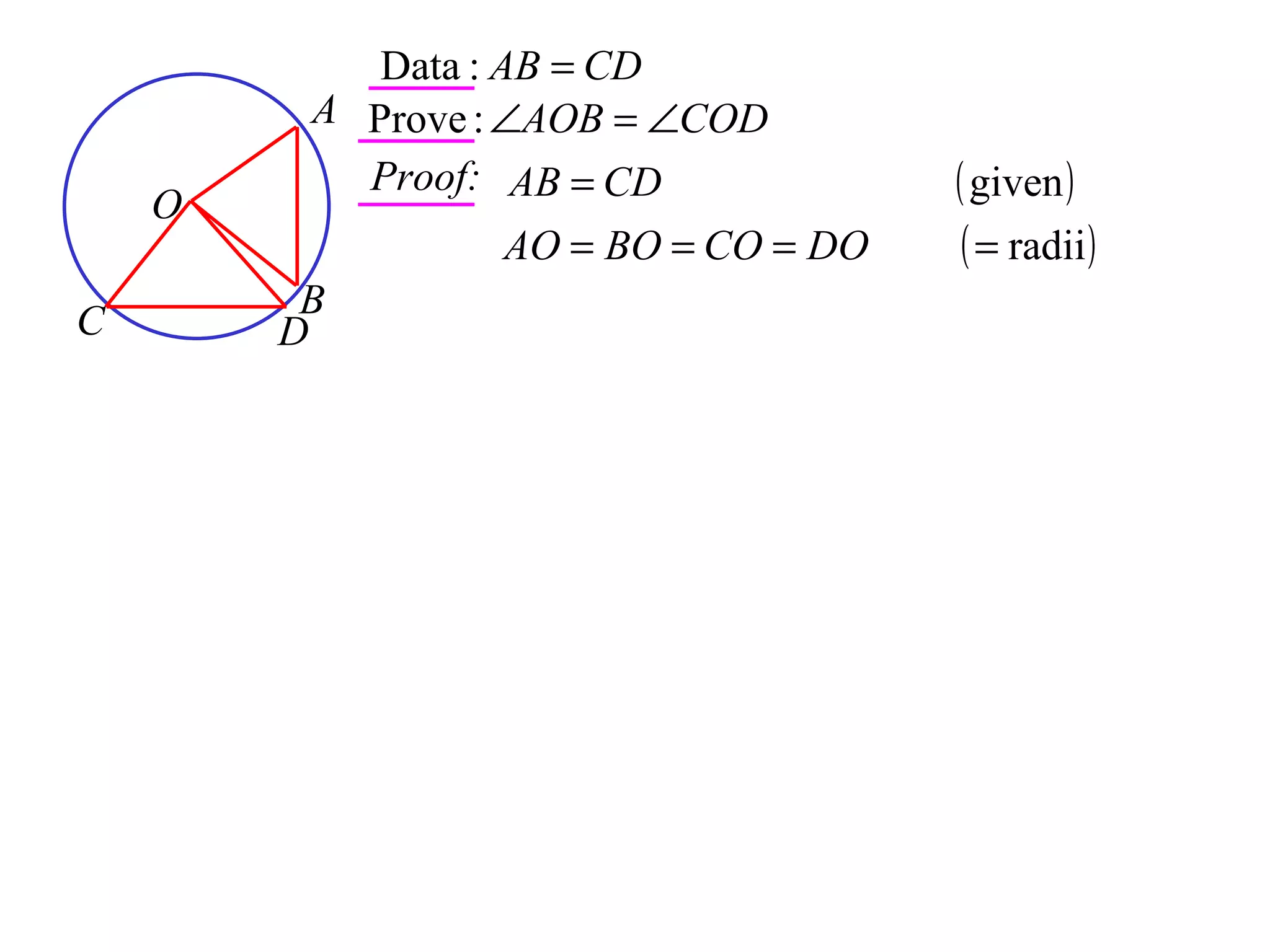
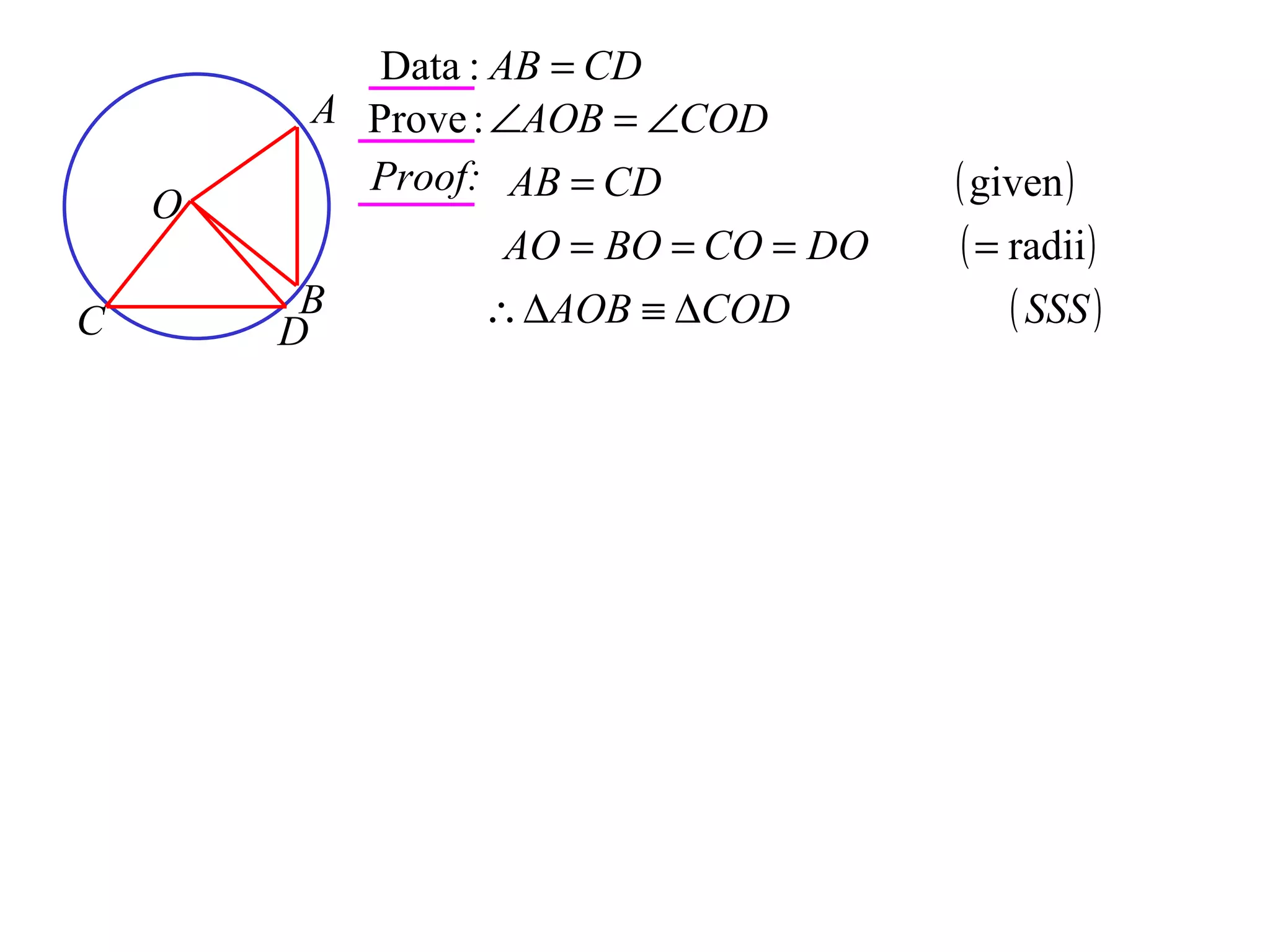
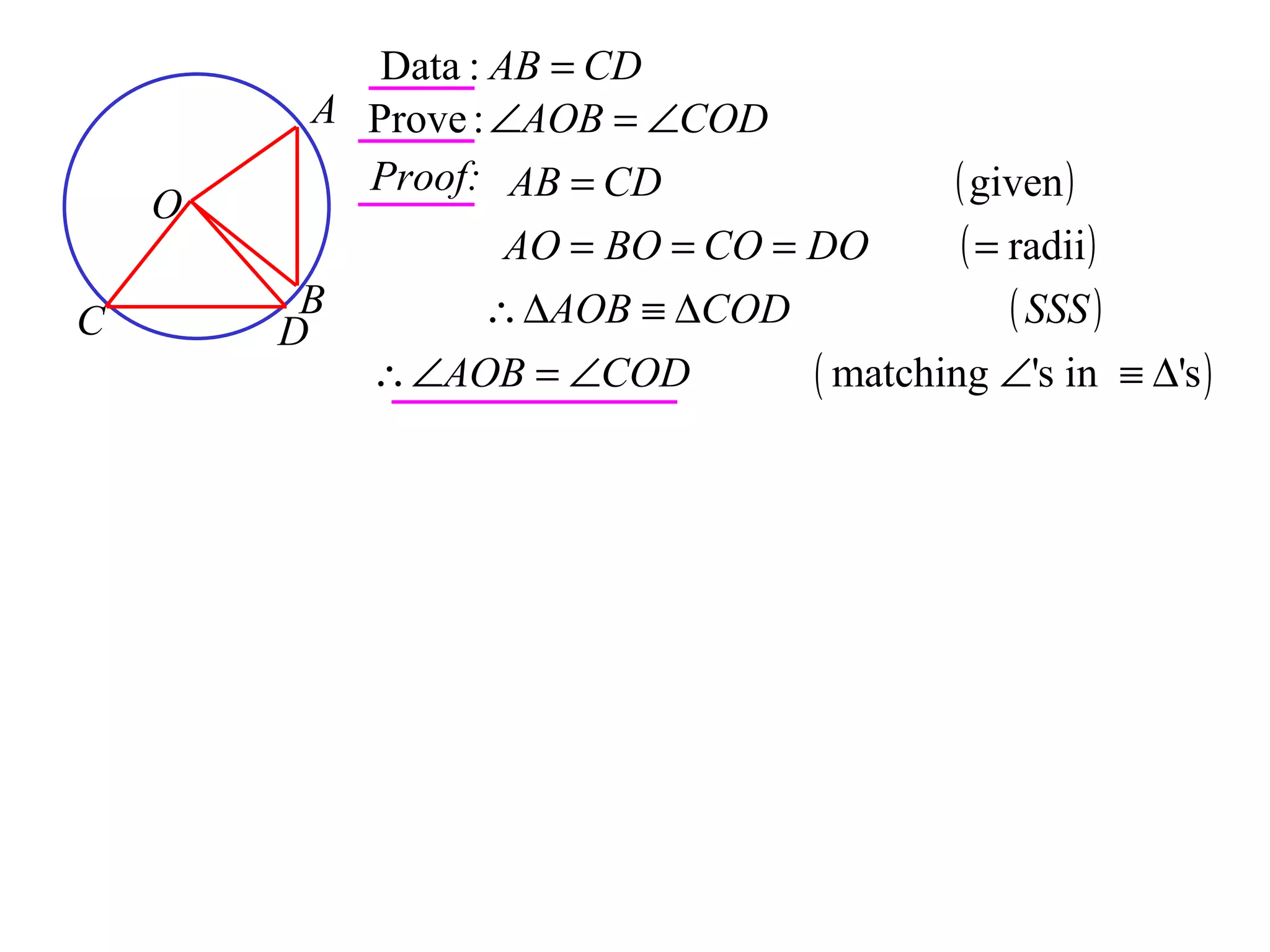
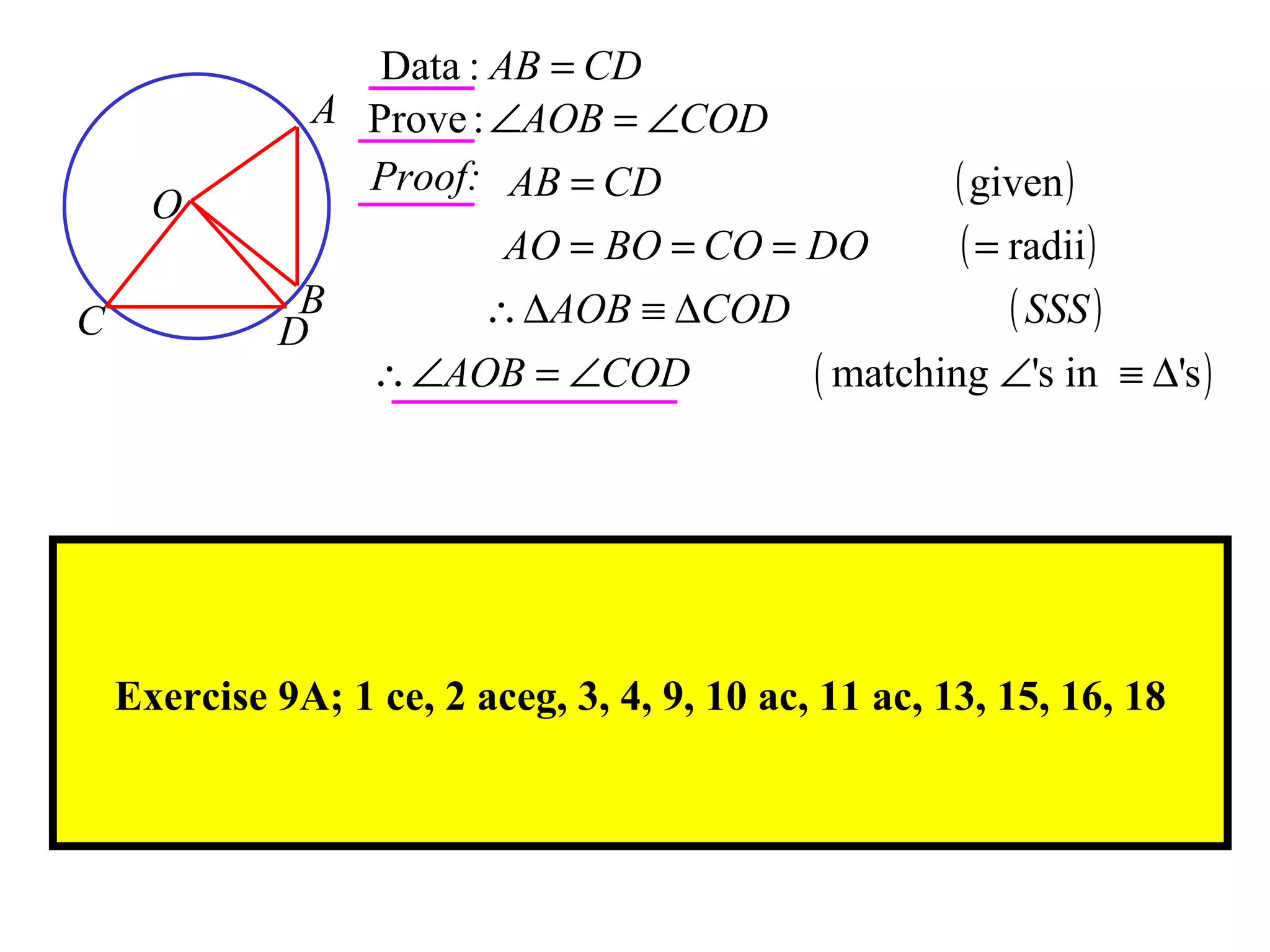
The document defines various terms related to circle geometry, including radius, diameter, chord, secant, tangent, arc, sector, segment, and more. It also presents several theorems regarding chords and arcs, such as a perpendicular from the circle's center bisects a chord, equal chords subtend equal angles at the center, and more. Diagrams with proofs are provided.

1. Circle Geometry

2. Circle Geometry Circle Geometry Definitions

3. Circle Geometry Circle Geometry Definitions

4. Circle Geometry Circle Geometry Definitions Radius: an interval joining centre to the circumference radius

5. Circle Geometry Circle Geometry Definitions Radius: an interval joining centre to the circumference radius Diameter: an interval passing through the centre, joining any two points on the circumference diameter

6. Circle Geometry Circle Geometry Definitions Radius: an interval joining centre to the circumference radius Diameter: an interval passing through the centre, joining any two points on the circumference diameter Chord: an interval joining two points on the circumference chord

7. Circle Geometry Circle Geometry Definitions Radius: an interval joining centre to the circumference radius Diameter: an interval passing through the centre, joining any two points on the circumference diameter Chord: an interval joining two points on the circumference chord Secant: a line that cuts the circle secant

8. Circle Geometry Circle Geometry Definitions Radius: an interval joining centre to the circumference radius Diameter: an interval passing through the centre, joining any two points on the circumference diameter Chord: an interval joining two points on the circumference chord Secant: a line that cuts the circle secant Tangent: a line that touches the circle tangent

9. Circle Geometry Circle Geometry Definitions Radius: an interval joining centre to the circumference radius Diameter: an interval passing through the centre, joining any two points on the circumference diameter Chord: an interval joining two points on the circumference chord Secant: a line that cuts the circle secant Tangent: a line that touches the circle tangent Arc: a piece of the circumference arc

11. Sector: a plane figure with two radii and an arc as boundaries. sector

12. Sector: a plane figure with two radii and an arc as boundaries. sector The minor sector is the small “piece of the pie”, the major sector is the large “piece”

13. Sector: a plane figure with two radii and an arc as boundaries. sector The minor sector is the small “piece of the pie”, the major sector is the large “piece” A quadrant is a sector where the angle at the centre is 90 degrees

14. Sector: a plane figure with two radii and an arc as boundaries. sector The minor sector is the small “piece of the pie”, the major sector is the large “piece” A quadrant is a sector where the angle at the centre is 90 degrees Segment: a plane figure with a chord and an arc as boundaries. segment

15. Sector: a plane figure with two radii and an arc as boundaries. sector The minor sector is the small “piece of the pie”, the major sector is the large “piece” A quadrant is a sector where the angle at the centre is 90 degrees Segment: a plane figure with a chord and an arc as boundaries. segment A semicircle is a segment where the chord is the diameter, it is also a sector as the diameter is two radii.

17. Concyclic Points: points that lie on the same circle. A B C D

18. Concyclic Points: points that lie on the same circle. concyclic points A B C D

19. Concyclic Points: points that lie on the same circle. concyclic points Cyclic Quadrilateral: a four sided shape with all vertices on the same circle. cyclic quadrilateral A B C D

21. A B

22. A B represents the angle subtended at the centre by the arc AB

23. A B represents the angle subtended at the centre by the arc AB

24. A B represents the angle subtended at the centre by the arc AB represents the angle subtended at the circumference by the arc AB

25. A B represents the angle subtended at the centre by the arc AB represents the angle subtended at the circumference by the arc AB

26. A B represents the angle subtended at the centre by the arc AB represents the angle subtended at the circumference by the arc AB Concentric circles have the same centre.

29. Circles touching internally share a common tangent.

30. Circles touching internally share a common tangent. Circles touching externally share a common tangent.

31. Circles touching internally share a common tangent. Circles touching externally share a common tangent.

32. Circles touching internally share a common tangent. Circles touching externally share a common tangent.

33. Chord (Arc) Theorems

34. Chord (Arc) Theorems Note: = chords cut off = arcs

35. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre.

36. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. A B O X

37. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. A B O X

38. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. A B O X

39. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. A B O X

40. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. Proof: Join OA , OB A B O X

41. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. Proof: Join OA , OB A B O X

42. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. Proof: Join OA , OB A B O X

43. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. Proof: Join OA , OB A B O X

44. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. Proof: Join OA , OB A B O X

45. Chord (Arc) Theorems Note: = chords cut off = arcs (1) A perpendicular drawn to a chord from the centre of a circle bisects the chord, and the perpendicular bisector of a chord passes through the centre. Proof: Join OA , OB A B O X

46. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles.

47. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. A B O X

48. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. A B O X

49. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. A B O X

50. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. A B O X

51. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

52. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

53. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

54. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

55. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

56. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

57. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

58. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

59. (2) Converse of (1) The line from the centre of a circle to the midpoint of the chord at right angles. Proof: Join OA , OB A B O X

60. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre.

61. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. A B O X C D Y

62. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. A B O X C D Y

63. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. A B O X C D Y

64. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. A B O X C D Y

65. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. A B O X C D Y

66. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

67. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

68. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

69. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

70. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

71. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

72. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

73. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

74. (3) Equal chords of a circle are the same distance from the centre and subtend equal angles at the centre. Proof: Join OA , OC A B O X C D Y

75. A B O C D

76. A B O C D

77. A B O C D

78. Proof: A B O C D

79. Proof: A B O C D

80. Proof: A B O C D

81. Proof: A B O C D

82. Proof: Exercise 9A; 1 ce, 2 aceg, 3, 4, 9, 10 ac, 11 ac, 13, 15, 16, 18 A B O C D