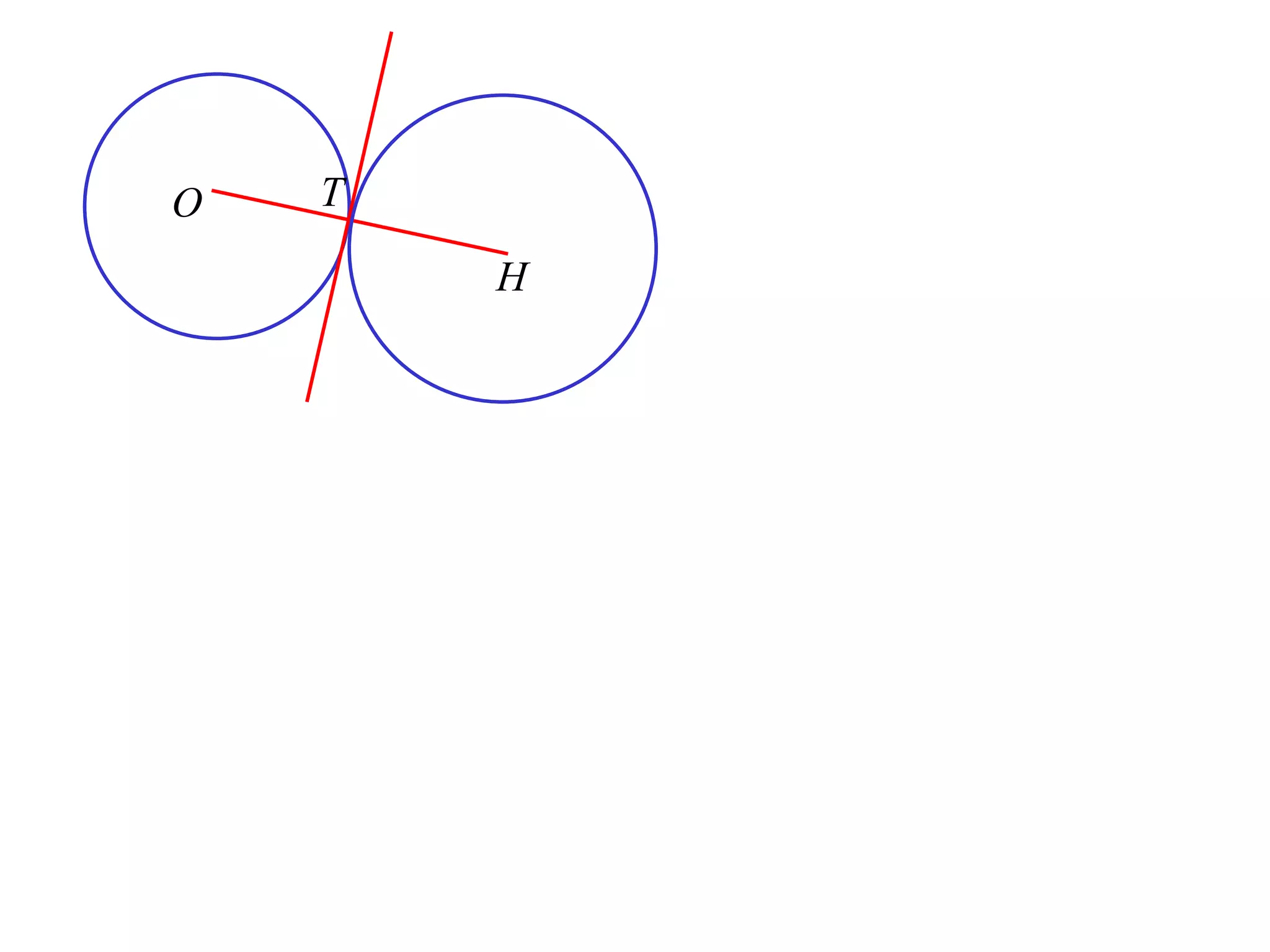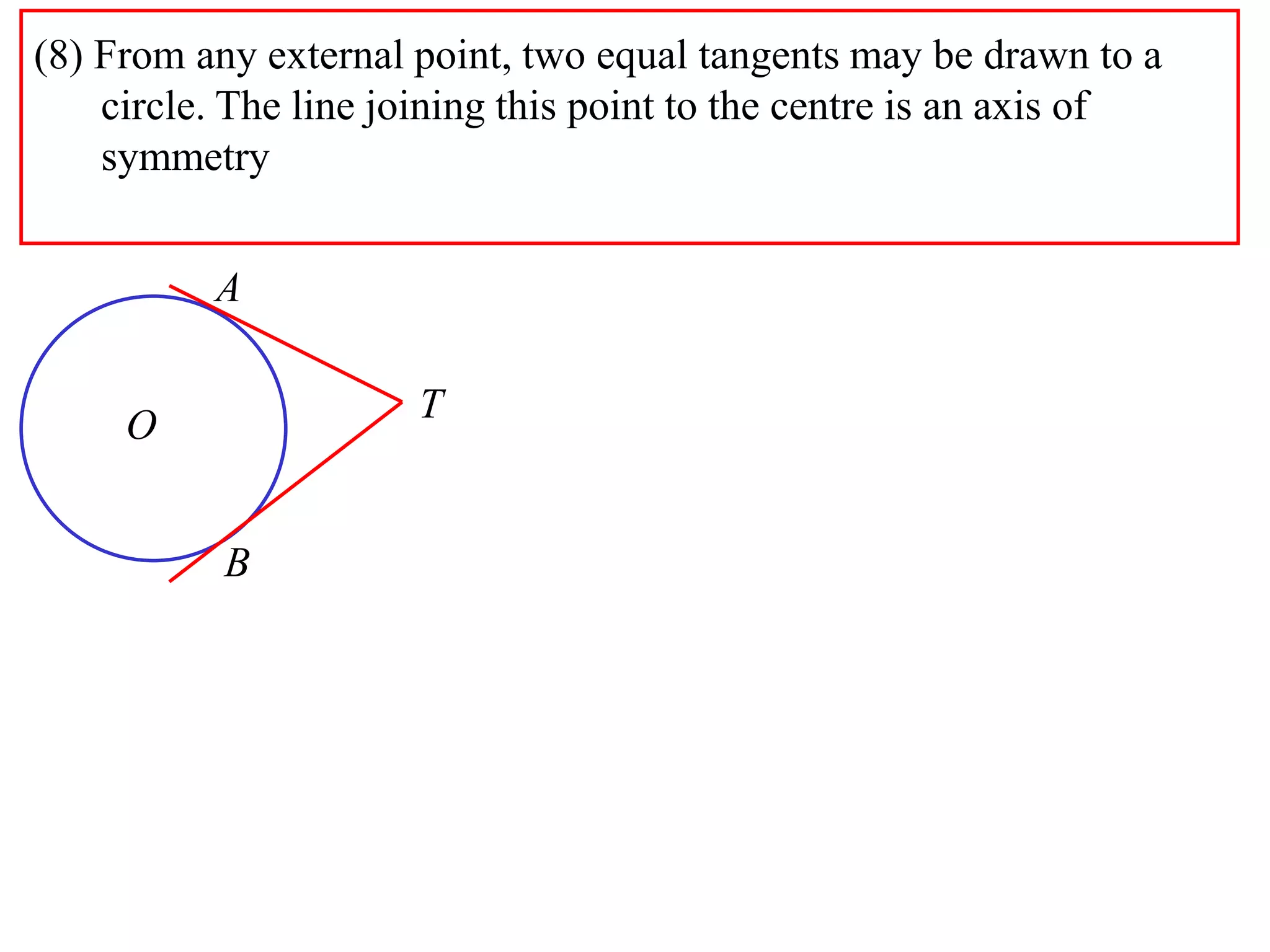
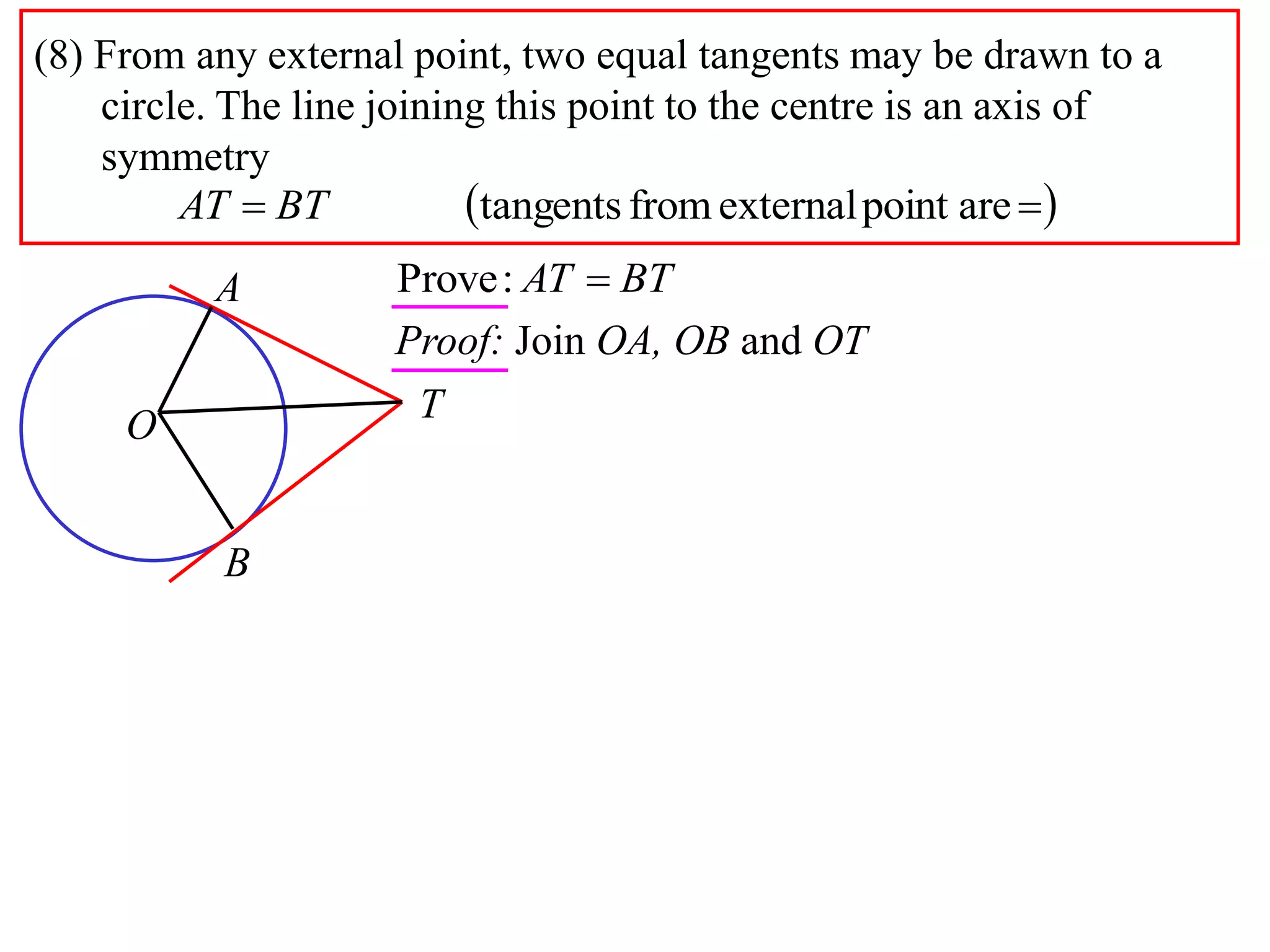
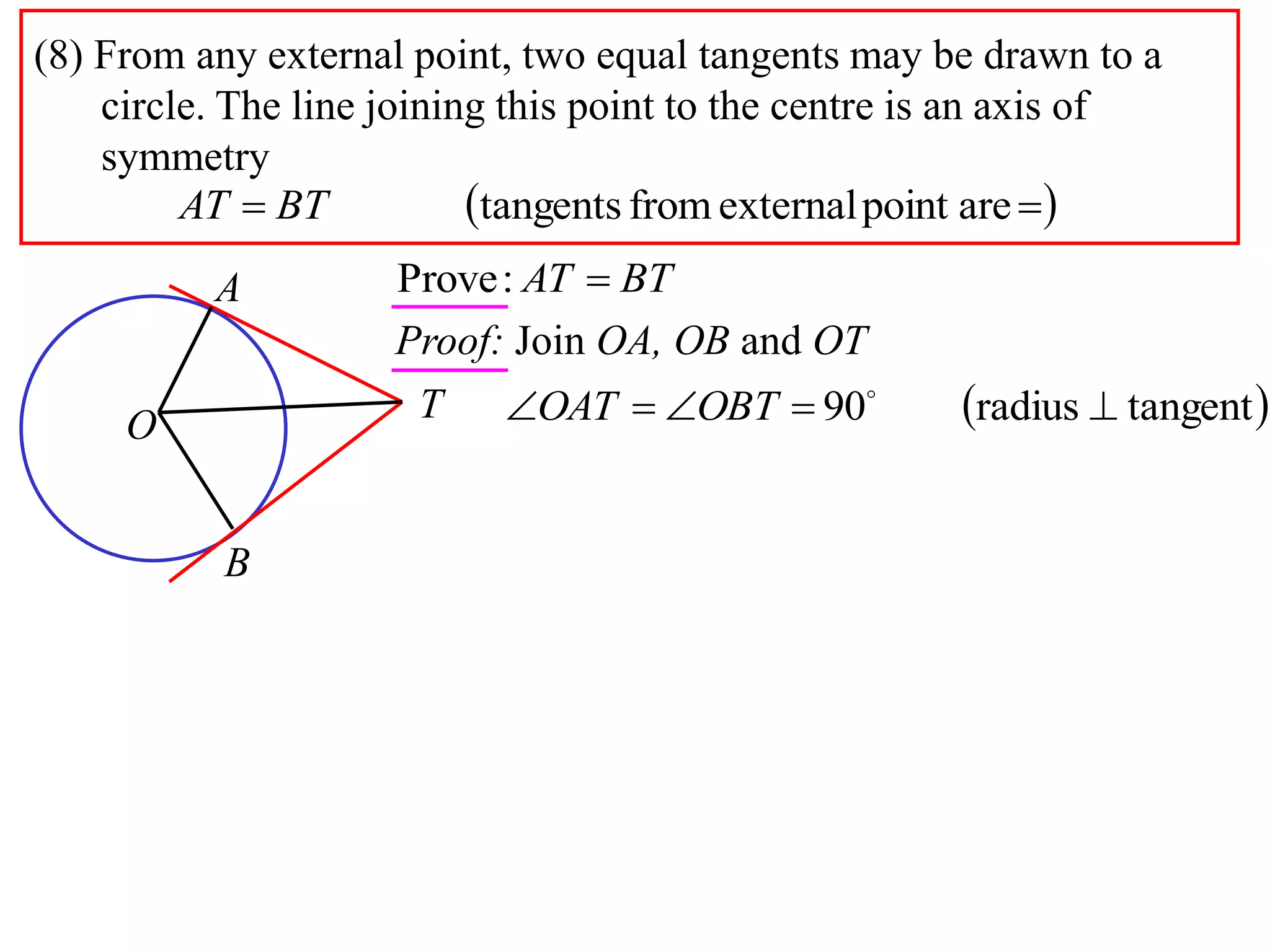
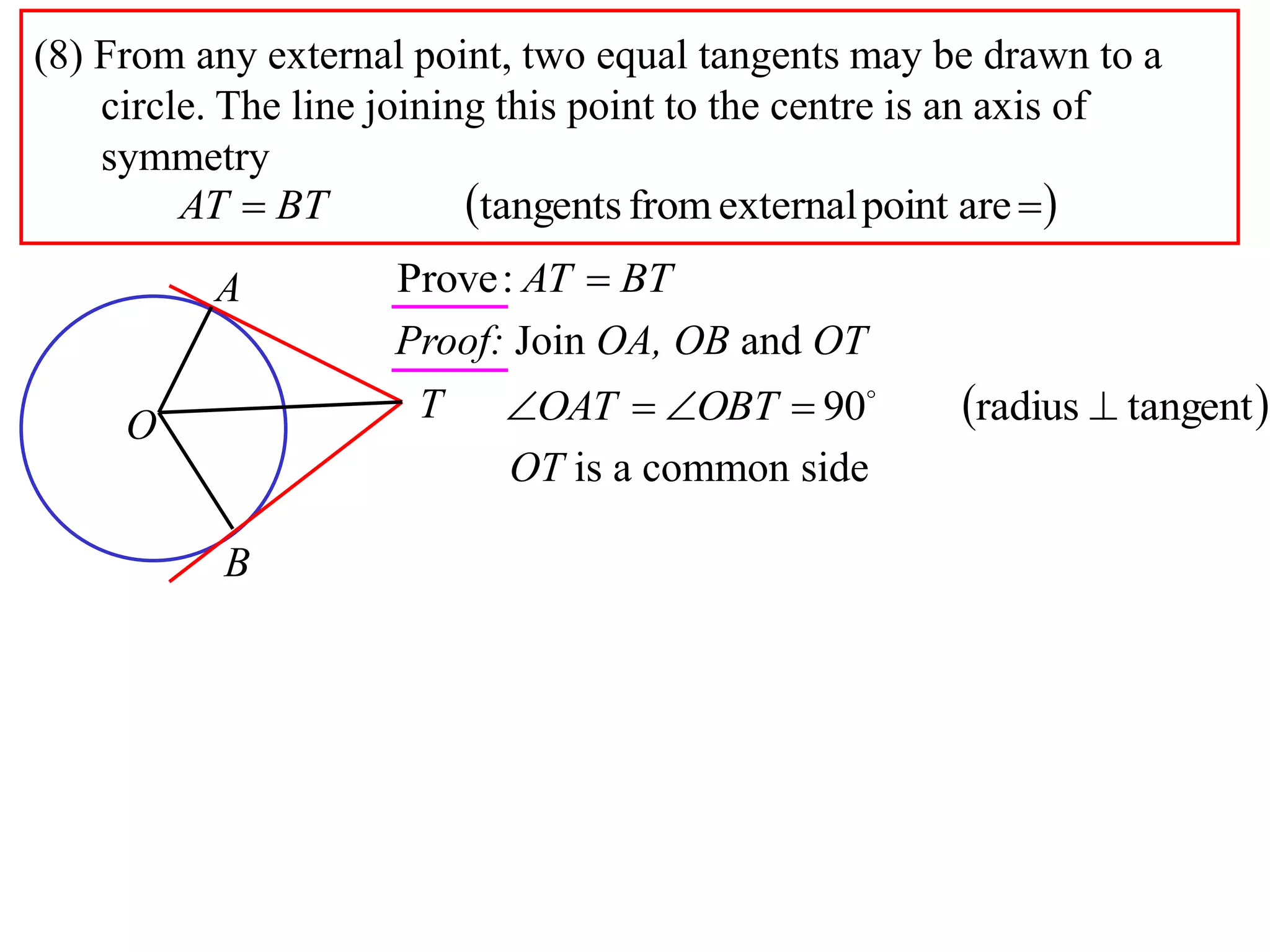
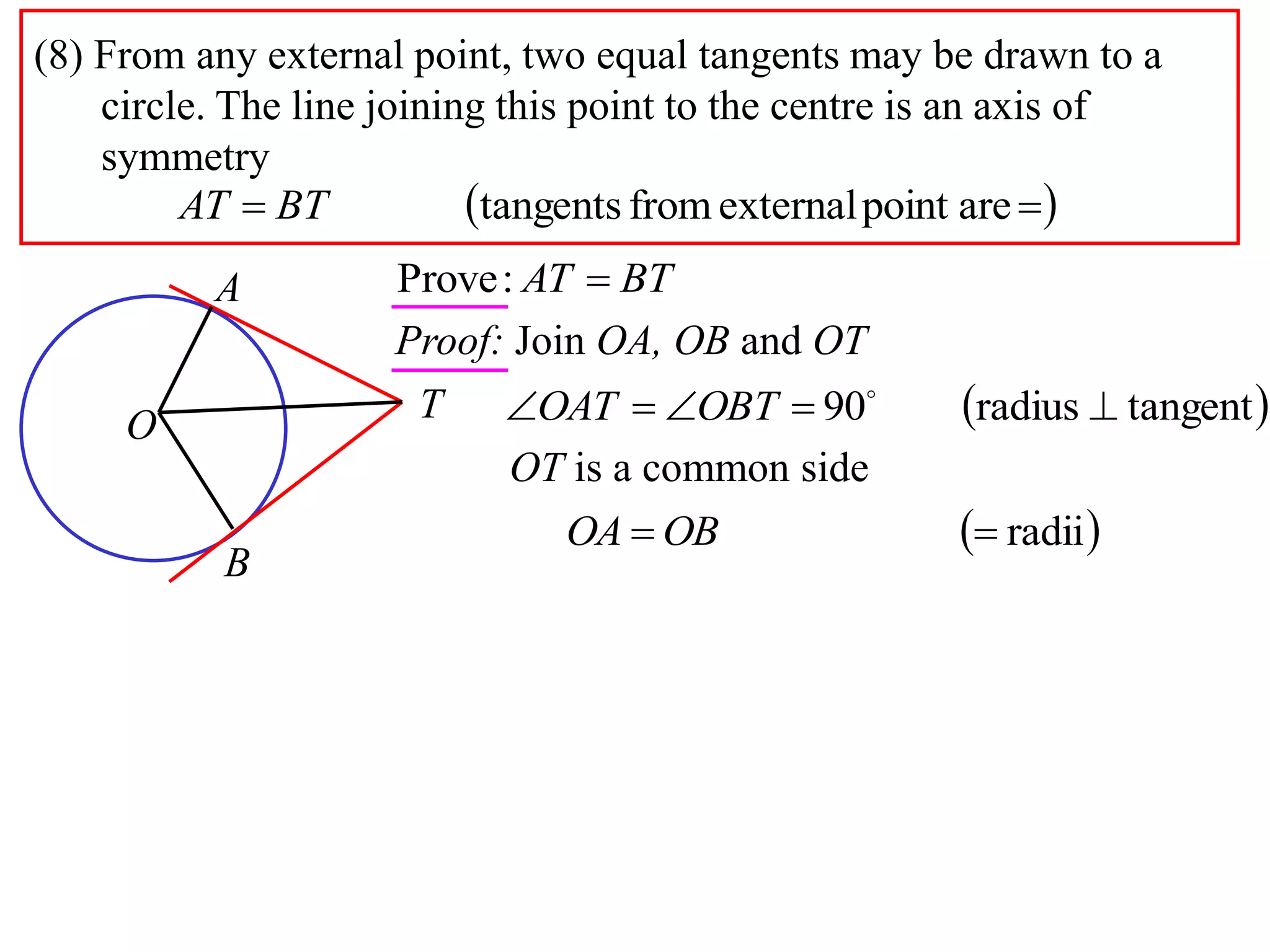
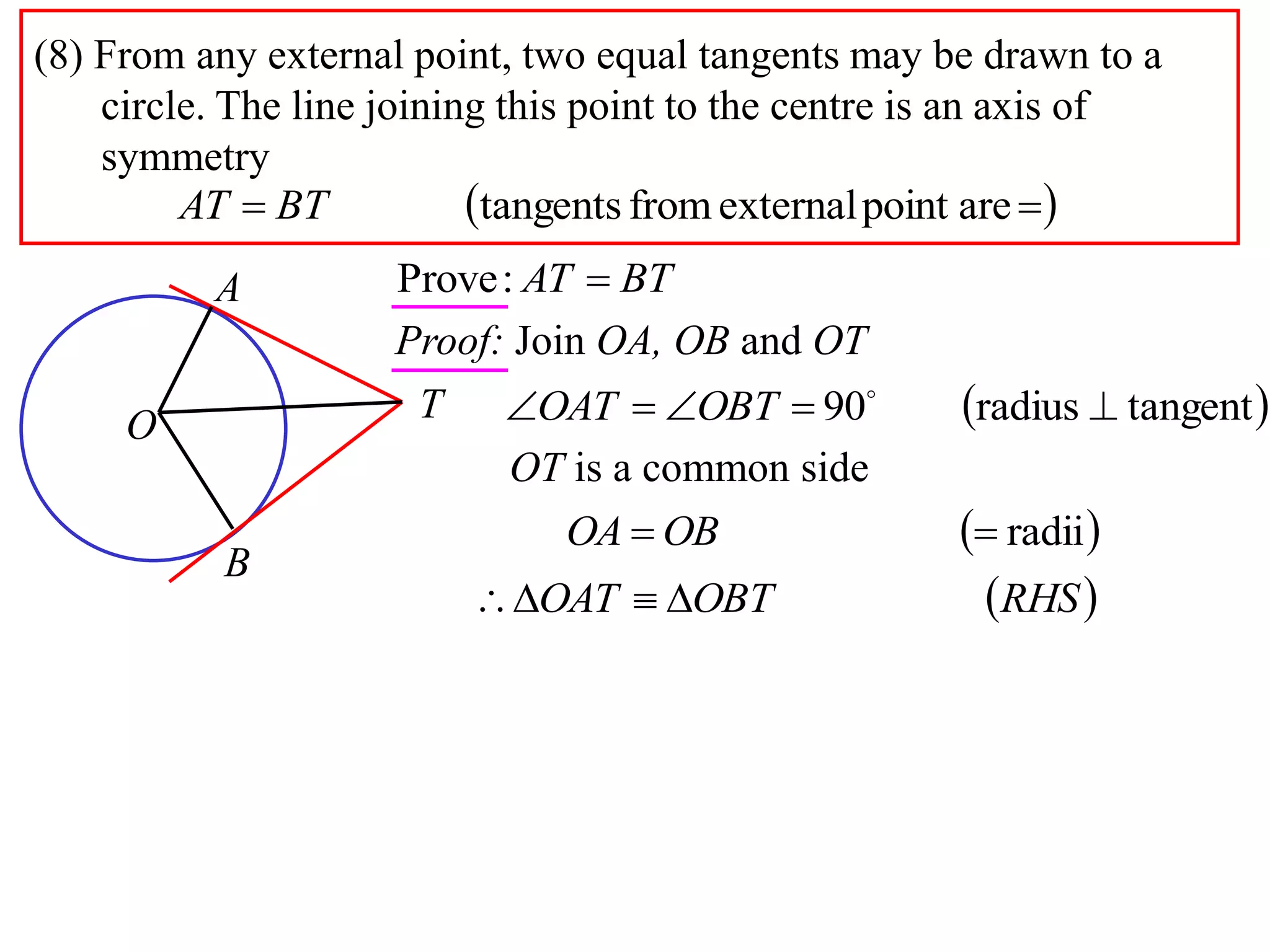
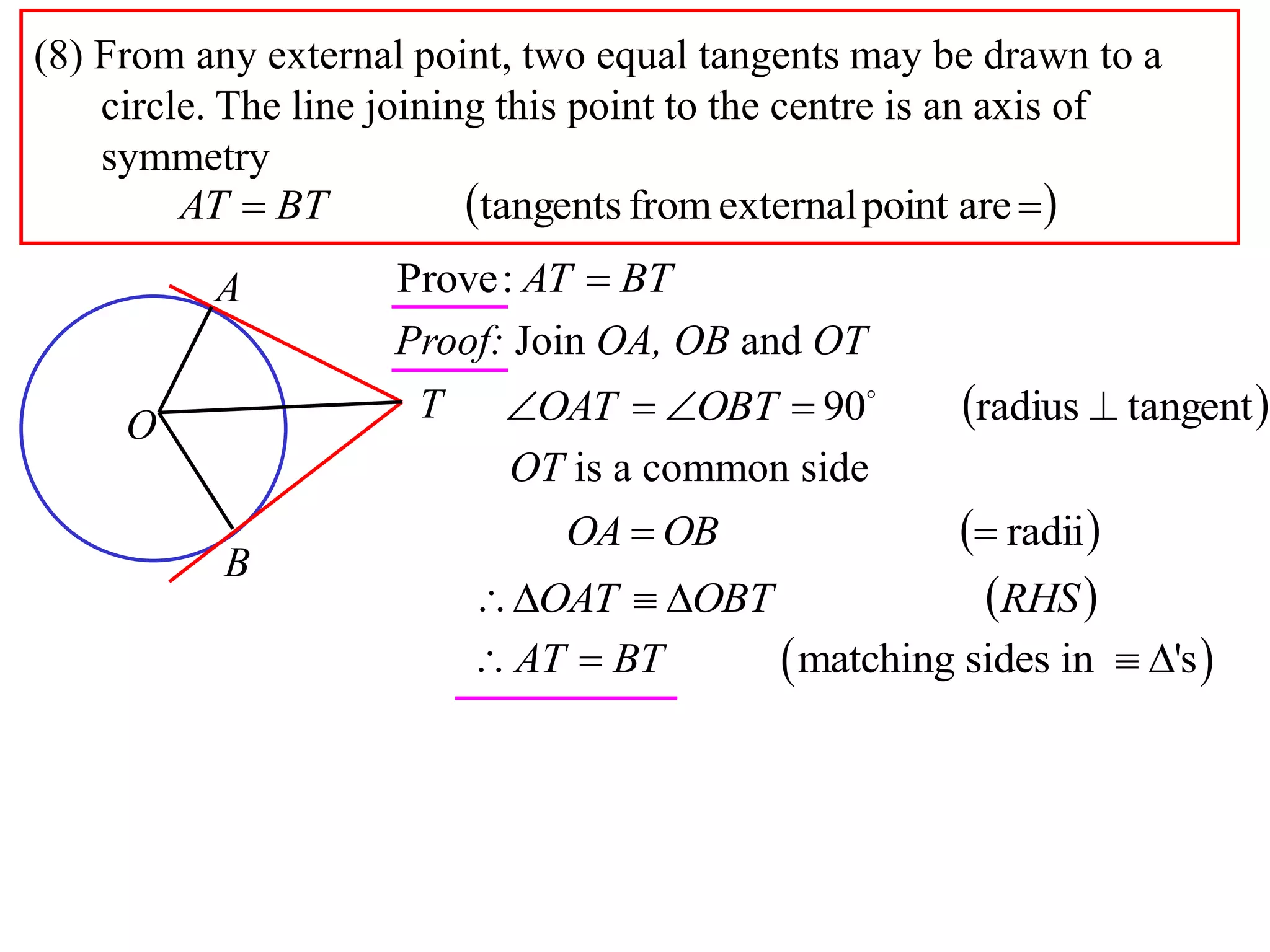
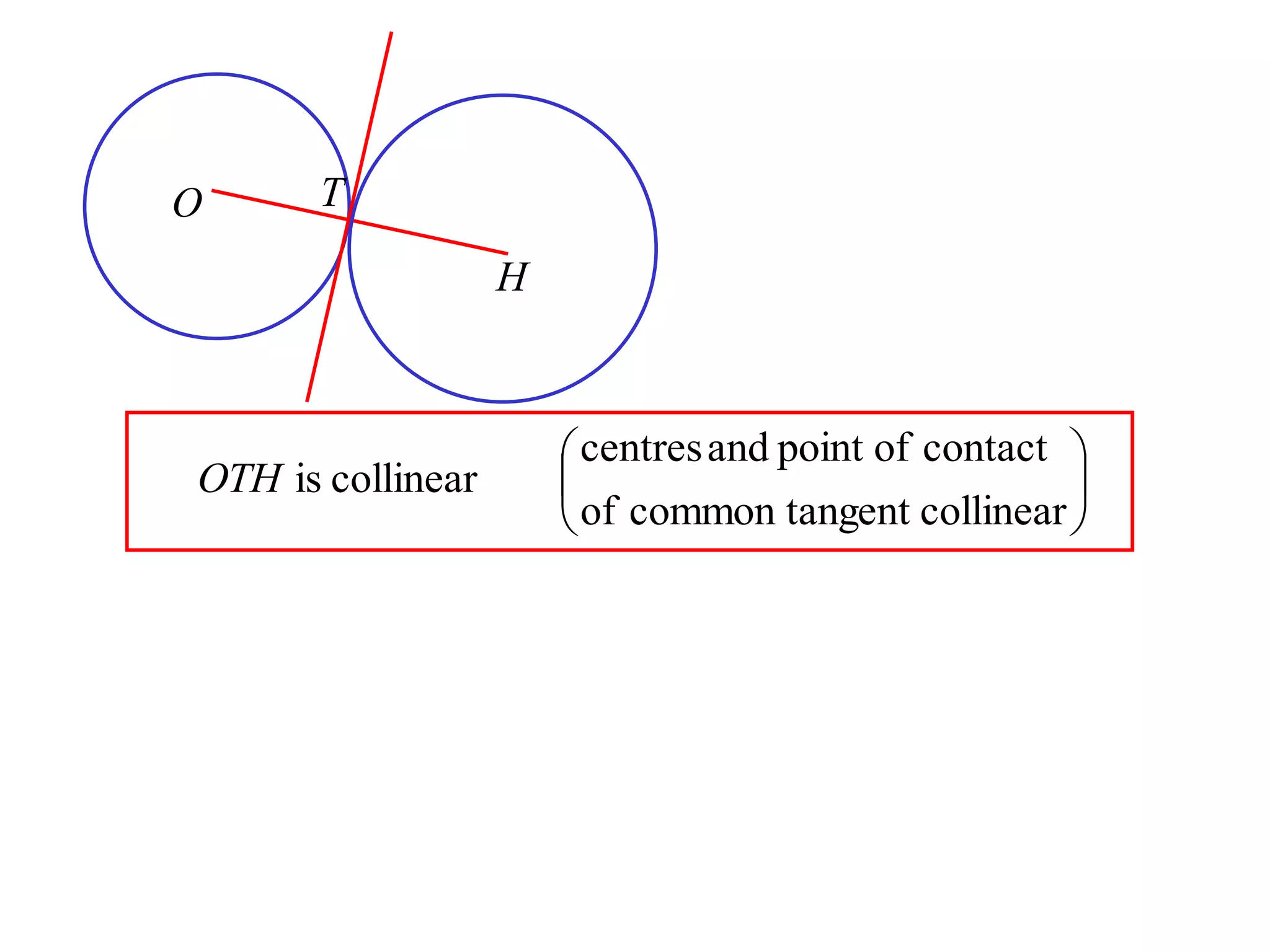
The document discusses several theorems related to tangents of circles: 1) The angle between a tangent line and radius drawn to the point of contact is 90 degrees. 2) Equal tangents can be drawn from any external point to a circle, and the line joining the point to the center is an axis of symmetry. 3) If two circles share a common tangent, the centers and point of contact must be collinear.

1. Tangent Theorems

2. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.

3. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 

4. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Z Let x be the distance of the chord from
the centre.
O x X
Y

5. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Z Let x be the distance of the chord from
the centre.
y Let 2y be the length of the chord.
O x X
y
Y

6. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Z Let x be the distance of the chord from
the centre.
y Let 2y be the length of the chord.
O x X
 line joining centre to 
y OX  YZ  
 midpoint,  to chord 
Y

7. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Z Let x be the distance of the chord from
the centre.
y Let 2y be the length of the chord.
O x X
 line joining centre to 
y OX  YZ  
 midpoint,  to chord 
Y As x  radius
y0

8. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Let x be the distance of the chord from
Z the centre.
y Let 2y be the length of the chord.
O x X
 line joining centre to 
y OX  YZ  
 midpoint,  to chord 
Y
As x  radius
y0

9. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Let x be the distance of the chord from
Z the centre.
y Let 2y be the length of the chord.
O xy X
 line joining centre to 
OX  YZ  
 midpoint,  to chord 
Y
As x  radius
y0

10. Tangent Theorems
(7) Assumption:
The size of the angle between a tangent and the radius drawn to the
point of contact is 90 degrees.
OX  XY radius  tangent 
Let x be the distance of the chord from
Z the centre.
Let 2y be the length of the chord.
O x X
 line joining centre to 
OX  YZ  
 midpoint,  to chord 
Y
As x  radius
y0

11. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry

12. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
A
T
O
B

13. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A
T
O
B

14. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
T
O
B

15. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
Proof: Join OA, OB and OT
T
O
B

16. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
Proof: Join OA, OB and OT
O T OAT  OBT  90 radius  tangent 
B

17. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
Proof: Join OA, OB and OT
O T OAT  OBT  90 radius  tangent 
OT is a common side
B

18. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
Proof: Join OA, OB and OT
O T OAT  OBT  90 radius  tangent 
OT is a common side
OA  OB  radii 
B

19. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
Proof: Join OA, OB and OT
O T OAT  OBT  90 radius  tangent 
OT is a common side
OA  OB  radii 
B
 OAT  OBT RHS 

20. (8) From any external point, two equal tangents may be drawn to a
circle. The line joining this point to the centre is an axis of
symmetry
AT  BT tangents from external point are 
A Prove : AT  BT
Proof: Join OA, OB and OT
O T OAT  OBT  90 radius  tangent 
OT is a common side
OA  OB  radii 
B
 OAT  OBT RHS 
 AT  BT  matching sides in  's 

21. O T
H

22. O T
H
 centres and point of contact 
OTH is collinear  
 of common tangent collinear 

23. O T
H
 centres and point of contact 
OTH is collinear  
 of common tangent collinear 
Exercise 9E; 1aceg, 2bdfh, 3ac, 4bd, 6bc, 9, 10ac, 12b, 14, 16a