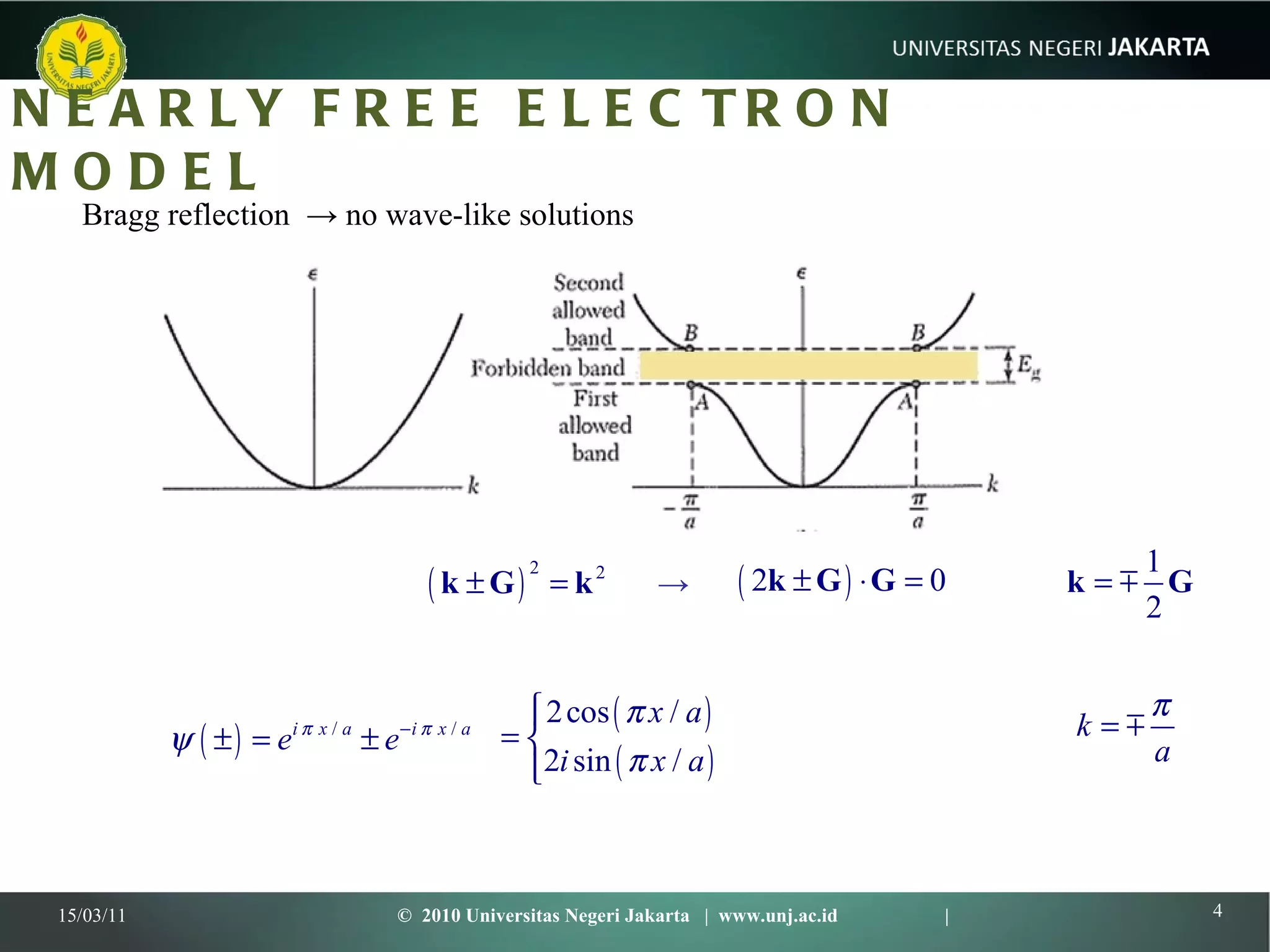
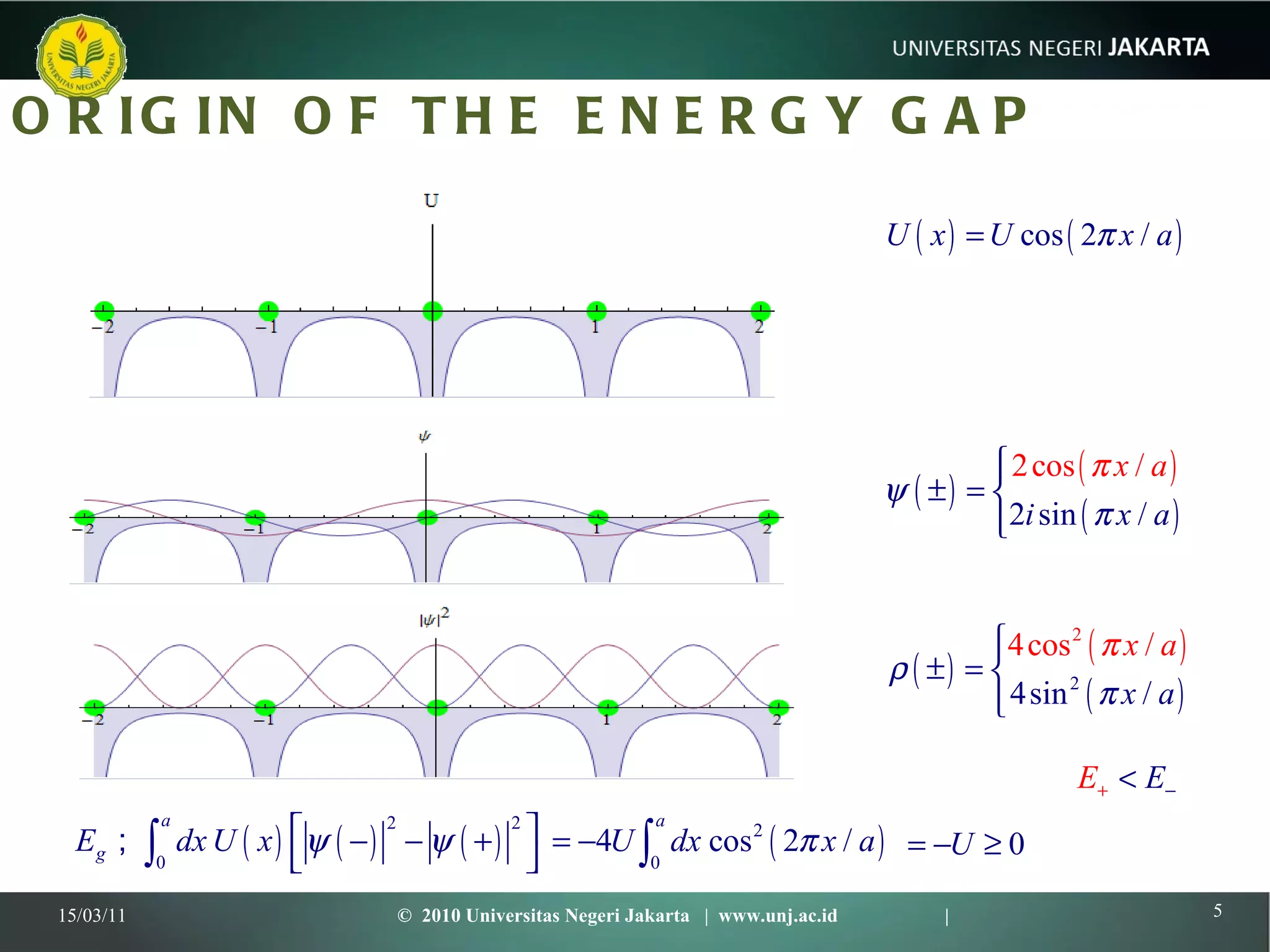
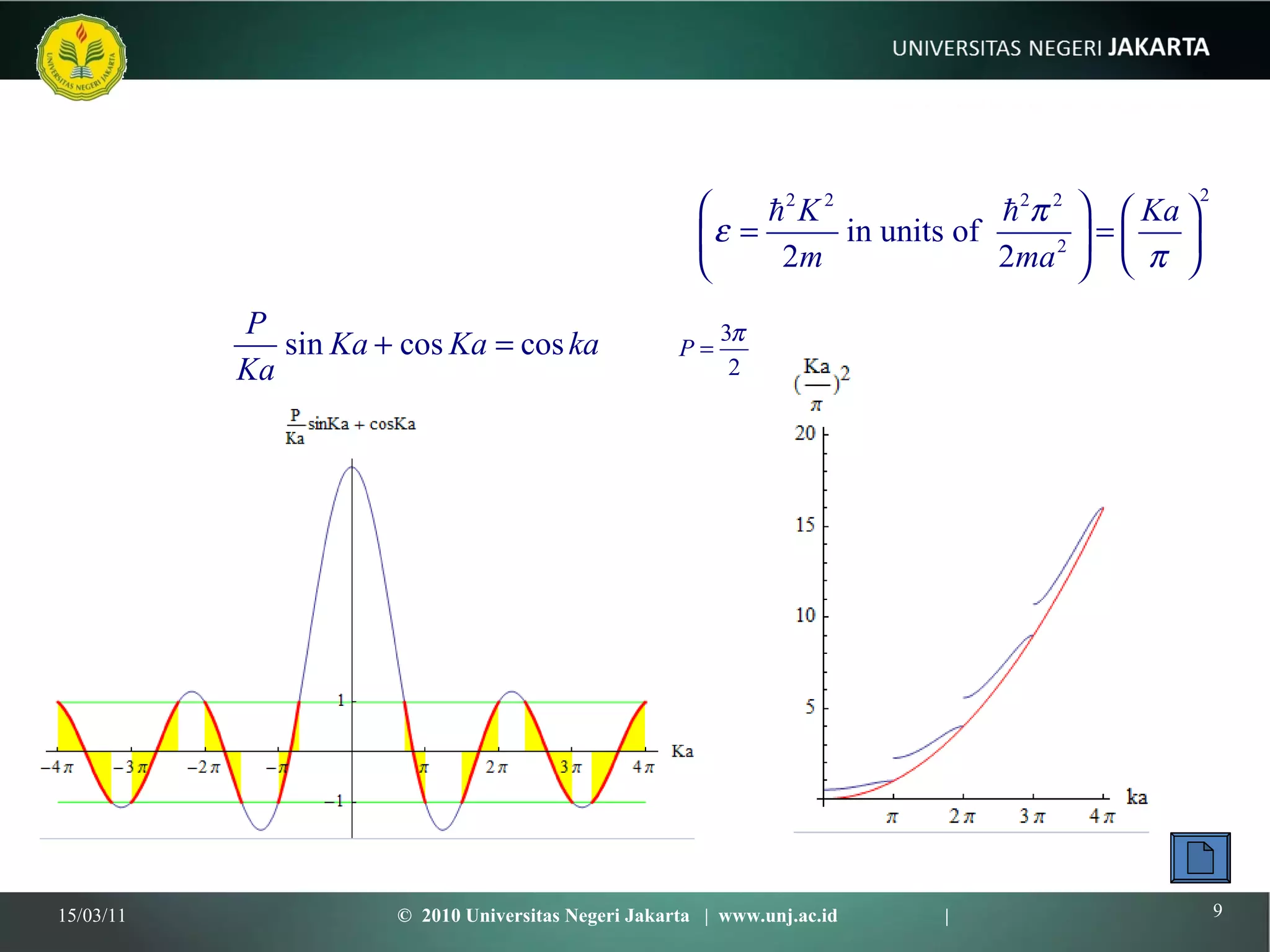
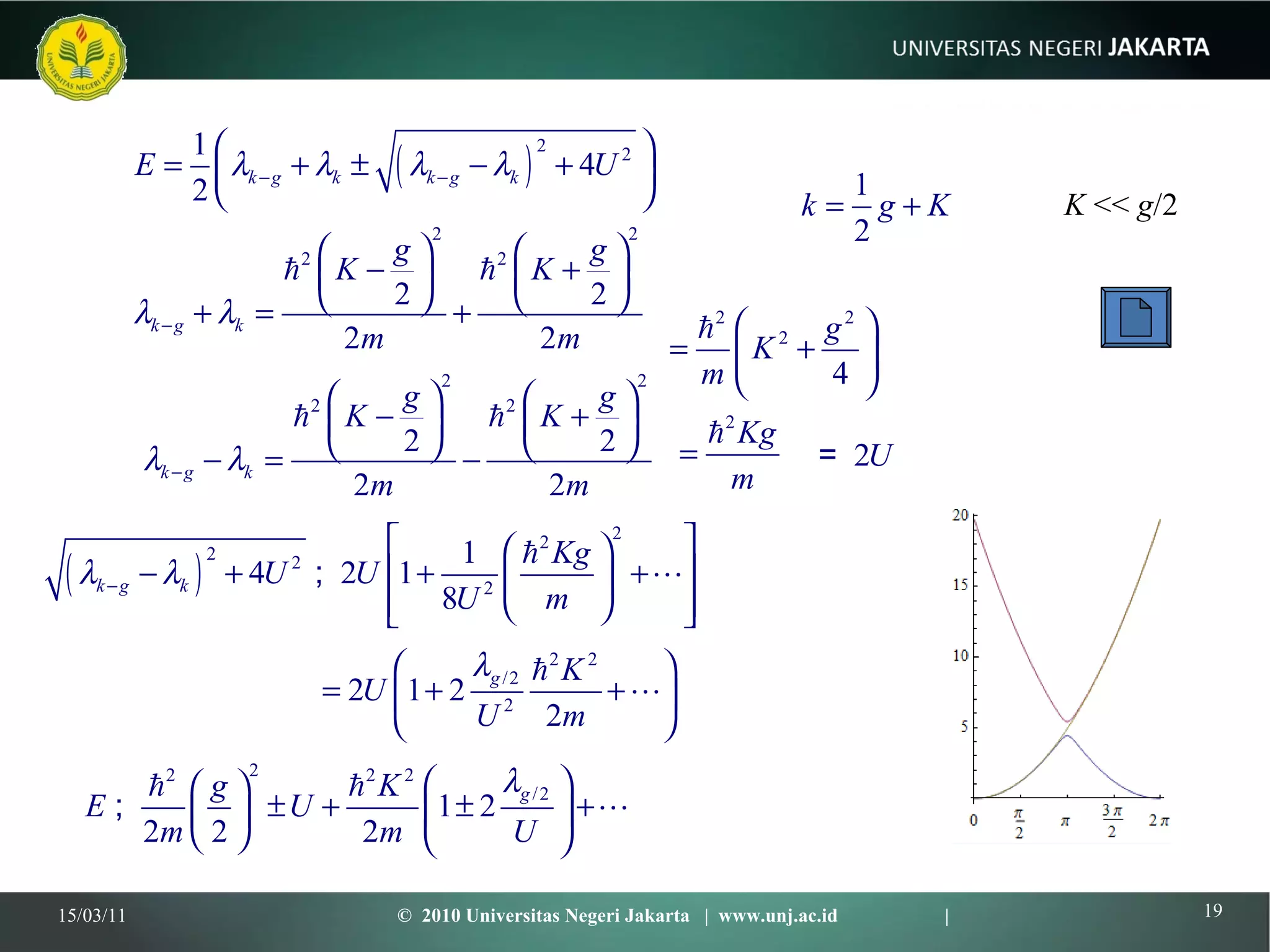
This document discusses several models for describing the band structure of solids, including the nearly free electron model, Kronig-Penney model, and Bloch theorem. It outlines the successes and limitations of the free electron model in explaining properties of metals, semiconductors, and insulators. The band model was developed to address these limitations through concepts like effective mass and energy gaps between bands. Specific models like Kronig-Penney use periodic potentials to understand the formation of energy bands and gaps.

1. Pertemuan 1 - 4 FISIKA ZAT PADAT Iwan Sugihartono, M.Si Jurusan Fisika Fakultas Matematika dan Ilmu Pengetahuan Alam

2. Outline Bloch Functions Nearly Free Electron Model Kronig-Penney Model Wave Equation of Electron in a Periodic Potential Number of Orbitals in a Band 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

3. Some successes of the free electron model: C, κ , σ , χ , … Some failures of the free electron model: Distinction between metals, semimetals, semiconductors & insulators. Positive values of Hall coefficent. Relation between conduction & valence electrons. Magnetotransport. Band model New concepts: Effective mass Holes finite T impurities 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

4. NEARLY FREE ELECTRON MODEL 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Bragg reflection -> no wave-like solutions -> energy gap Bragg condition: ->

5. ORIGIN OF THE ENERGY GAP 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

6. BLOCH FUNCTIONS 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Periodic potential -> Translational symmetry -> Abelian group T = { T ( R l )} k -representation of T ( R l ) is Corresponding basis function for the Schrodinger equation must satisfy This can be satisfied by the Bloch function where or -> representative values of k are contained inside the Brillouin zone. Basis =

7. KRONIG-PENNEY MODEL 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Bloch theorem: ψ  (0) continuous: ψ  ( a ) continuous: ψ (0) continuous: ψ ( a ) continuous:

8. -> Delta function potential: Thus so that 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

9. 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

10. MATRIX MECHANICS 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Ansatz Secular equation: Matrix equation Orthonormal basis: Eigen-problem

11. FOURIER SERIES OF THE PERIODIC POTENTIAL 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | ->  = Volume of crystal   volume of unit cell For a lattice with atomic basis at positions ρ α in the unit cell is the structural factor ->

12. PLANE WAVE EXPANSION 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Bloch function  = Volume of crystal Matrix form of the Schrodinger equation: (central equation) n = 0:

13. CRYSTAL MOMENTUM OF AN ELECTRON 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Properties of k : -> U = 0 -> Selection rules in collision processes -> crystal momentum of electron is  k . Eq., phonon absorption:

14. SOLUTION OF THE CENTRAL EQUATION 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | 1-D lattice, only

15. KRONIG-PENNEY MODEL IN RECIPROCAL SPACE 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Eigen-equation: -> (only s = 0 term contributes)

16. -> (Kronig-Penney model) with 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

17. EMPTY LATTICE APPROXIMATION 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Free electron in vacuum: Free electron in empty lattice: Simple cubic

18. APPROXIMATE SOLUTION NEAR A ZONE BOUNDARY 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | k near zone right boundary: Weak U , λ k  2 g >> U -> for E near λ k

19. K << g /2 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

20. 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

21. NUMBER OF ORBITALS IN A BAND 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Linear crystal of length L composed of of N cells of lattice constant a . Periodic boundary condition: -> -> N inequivalent values of k Generalization to 3-D crystals: Number of k points in 1 st BZ = Number of primitive cells -> Each primitive cell contributes one k point to each band. Crystals with odd numbers of electrons in primitive cell must be metals, e.g., alkali & noble metals metal semi-metal insulator

22. THANK YOU 15/03/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |