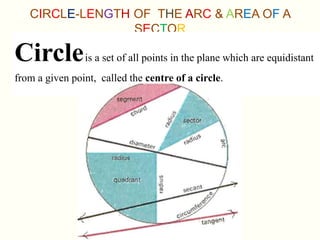
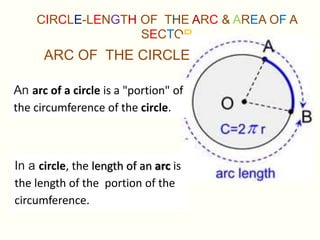
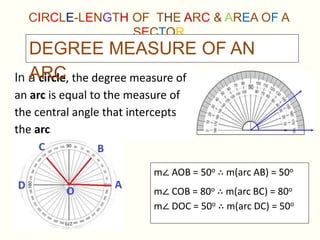
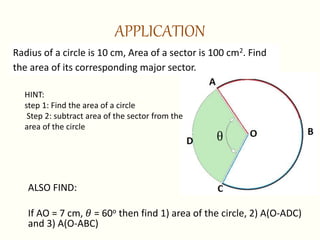
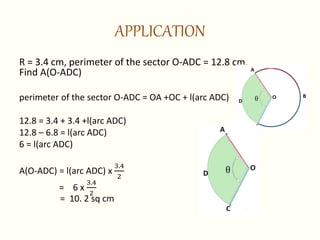
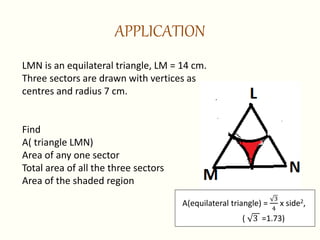
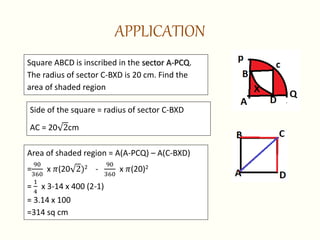
This document discusses circles, arcs, sectors, and how to calculate their properties. It defines a circle as all points equidistant from a center point, and an arc as a portion of a circle's circumference. The length of an arc is calculated by taking the ratio of the arc's central angle measure to 360 degrees and multiplying by 2πr. Similarly, the area of a sector is calculated by taking the ratio of its central angle measure to 360 degrees and multiplying by πr^2. Several examples are provided to demonstrate calculating arc lengths and sector areas.

1. MENSURATION-sk
CIRCLE-LENGTH OF THE ARC & AREA OF A SECTOR
STD X
MAHARASHTRA STATE BOARD OF EDUCATION,
MUMBAI

2. CIRCLE-LENGTH OF THE ARC & AREA OF A
SECTOR
Circleis a set of all points in the plane which are equidistant
from a given point, called the centre of a circle.

3. CIRCLE-LENGTH OF THE ARC & AREA OF A
SECTOR
An arc of a circle is a "portion" of
the circumference of the circle.
In a circle, the length of an arc is
the length of the portion of the
circumference.
ARC OF THE CIRCLE

4. CIRCLE-LENGTH OF THE ARC & AREA OF A
SECTOR
In a circle, the degree measure of
an arc is equal to the measure of
the central angle that intercepts
the arc.
DEGREE MEASURE OF AN
ARC
m∠ AOB = 50o ∴ m(arc AB) = 50o
m∠ COB = 80o ∴ m(arc BC) = 80o
m∠ DOC = 50o ∴ m(arc DC) = 50o

5. CIRCLE-LENGTH OF THE ARC & AREA OF A SECTOR
LENGTH OF THE ARC
Measure of
the arc (𝜃)
𝜃
360
Length of the
arc
360o 360
360
=1 1 x 2𝜋r
180o 180
360
=
1
2
1
2
x 2𝜋r
900 90
360
=
1
4
1
4
x 2𝜋r
60o 60
360
=
1
6
1
6
x 2𝜋r
45O 45
360
=
1
8
1
8
x 2𝜋r
𝜃o 𝜃
360
𝜃
360
x 2𝜋r
LENGTH (ARC) =
𝜃
360
x 2𝜋r

6. CIRCLE-LENGTH OF THE ARC & AREA OF A
SECTOR
A circular sector or circle sector, is the
portion of a circle enclosed by two radii
and an arc.
SECTOR of a circle

7. CIRCLE-LENGTH OF THE ARC & AREA OF A
SECTOR
Measure of
the arc (𝜃)
𝜃
360
Area of the
sector
360o 360
360
=1 1 x 𝜋r2
180o 180
360
=
1
2
1
2
x 𝜋r2
900 90
360
=
1
4
1
4
x 𝜋r2
60o 60
360
=
1
6
1
6
x 𝜋r2
45O 45
360
=
1
8
1
8
x 𝜋r2
𝜃o 𝜃
360
𝜃
360
x 𝜋r2
A (sector) =
𝜃
360
x 𝜋r2
AREA OF A SECTOR

8. CIRCLE-LENGTH OF THE ARC &
AREA OF A SECTOR
A (sector) =
𝜃
360
x 𝜋r2
LENGTH (ARC) =
𝜃
360
x 2𝜋r
A(SECTOR) = l(ARC) X
𝑅
2

9. APPLICATION
Radius of a circle is 10 cm. Measure of an arc
of the circle is 54o. Find the l(arc) and area of
the sector.
R = 10cm, 𝜃 =54o
l (arc)=
𝜃
360
x 2𝜋r
=
54
360
x 2 x 3.14 x 10 = 9.42 cm

10. Radius of a circle is 10 cm, Area of a sector is 100 cm2. Find
the area of its corresponding major sector.
APPLICATION
ALSO FIND:
If AO = 7 cm, 𝜃 = 60o then find 1) area of the circle, 2) A(O-ADC)
and 3) A(O-ABC)
HINT:
step 1: Find the area of a circle
Step 2: subtract area of the sector from the
area of the circle

11. APPLICATION
R = 3.4 cm, perimeter of the sector O-ADC = 12.8 cm.
Find A(O-ADC)
perimeter of the sector O-ADC = OA +OC + l(arc ADC)
12.8 = 3.4 + 3.4 +l(arc ADC)
12.8 – 6.8 = l(arc ADC)
6 = l(arc ADC)
A(O-ADC) = l(arc ADC) x
3.4
2
= 6 x
3.4
2
= 10. 2 sq cm

12. APPLICATION
PQ = 14cm, QR = 21 cm. PQRS is a rectangle
Find area of X,Y and Z regions.
Hint: step 1: find a(rectangle)
step 2: Find radius of sector X and Y region.
step 3: find area of sectors X and Y
step 4: subtract the sum of the area of
sectors X and Y from area of rectangle.

13. APPLICATION
LMN is an equilateral triangle, LM = 14 cm.
Three sectors are drawn with vertices as
centres and radius 7 cm.
Find
A( triangle LMN)
Area of any one sector
Total area of all the three sectors
Area of the shaded region
A(equilateral triangle) =
3
4
x side2,
( 3 =1.73)

14. APPLICATION
A (circle) = 𝜋r2= 36 𝜋 sq cm
A(sector) =
𝜃
360
x 𝜋r2
15𝜋 x 360= 𝜃 x 36 𝜋
𝜃 =1500
R = 6cm, A(sector) = 15𝜋 sq cm. Find: measure of the
arc(𝜃) and length of the arc corresponding to the sector
A(sector) = l(arc) x
𝑟
2
15𝜋 = l(arc) x 3
5𝜋 cm = l(arc)

15. APPLICATION
Square ABCD is inscribed in the sector A-PCQ.
The radius of sector C-BXD is 20 cm. Find the
area of shaded region
Side of the square = radius of sector C-BXD
AC = 20 2cm
Area of shaded region = A(A-PCQ) – A(C-BXD)
=
90
360
x 𝜋(20 2)2 -
90
360
x 𝜋(20)2
=
1
4
x 3-14 x 400 (2-1)
= 3.14 x 100
=314 sq cm

16. THANK YOU