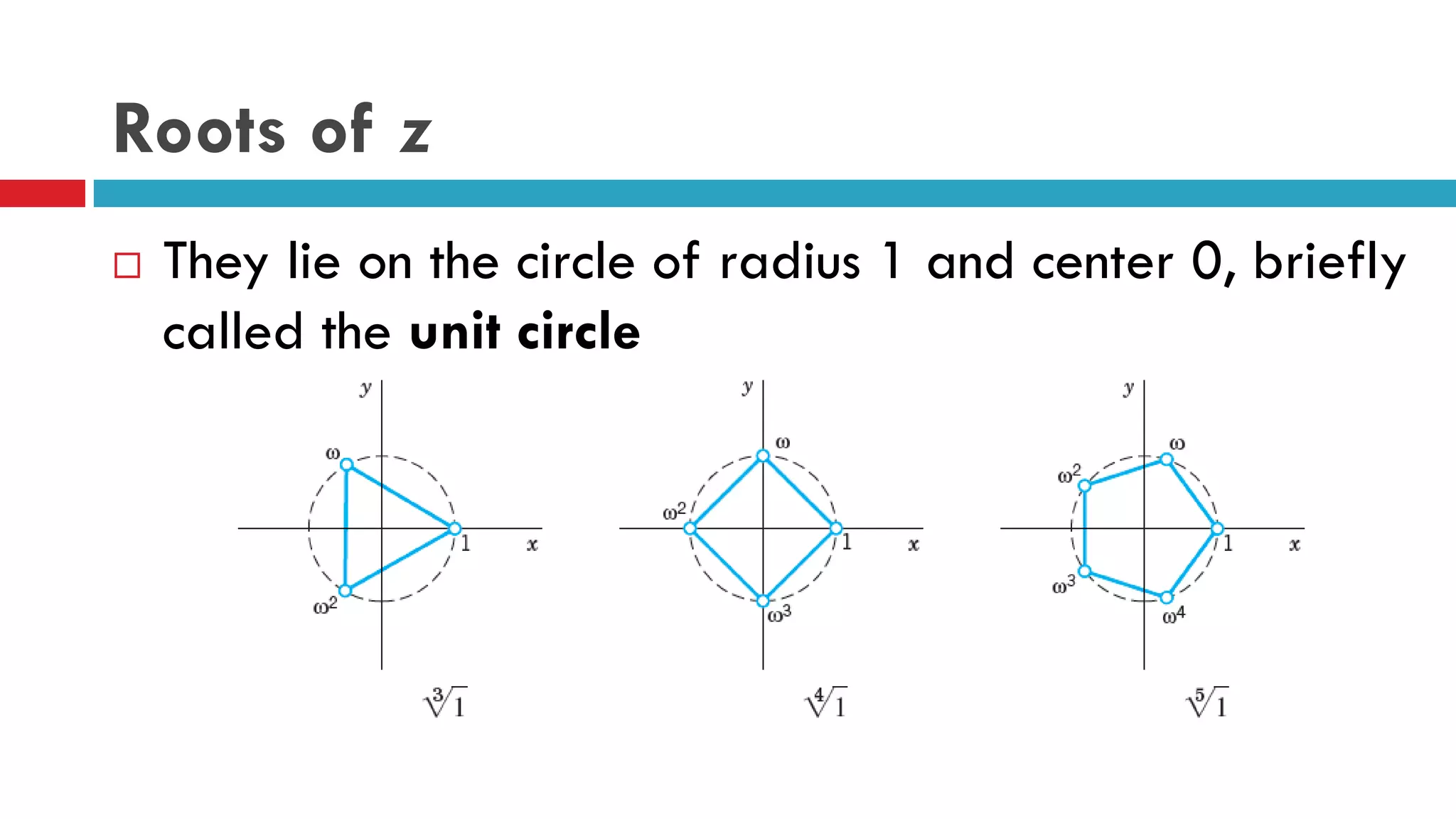
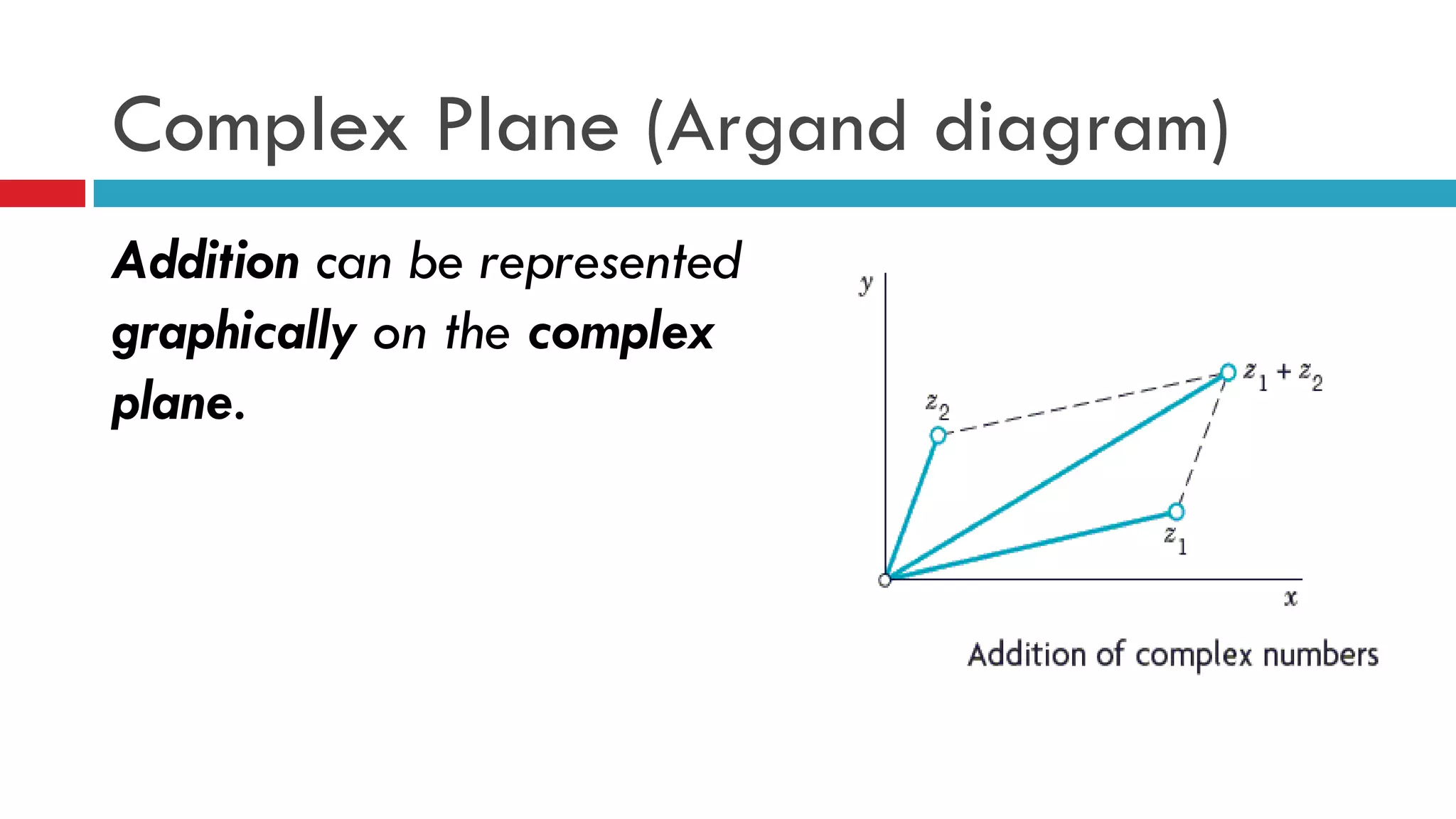
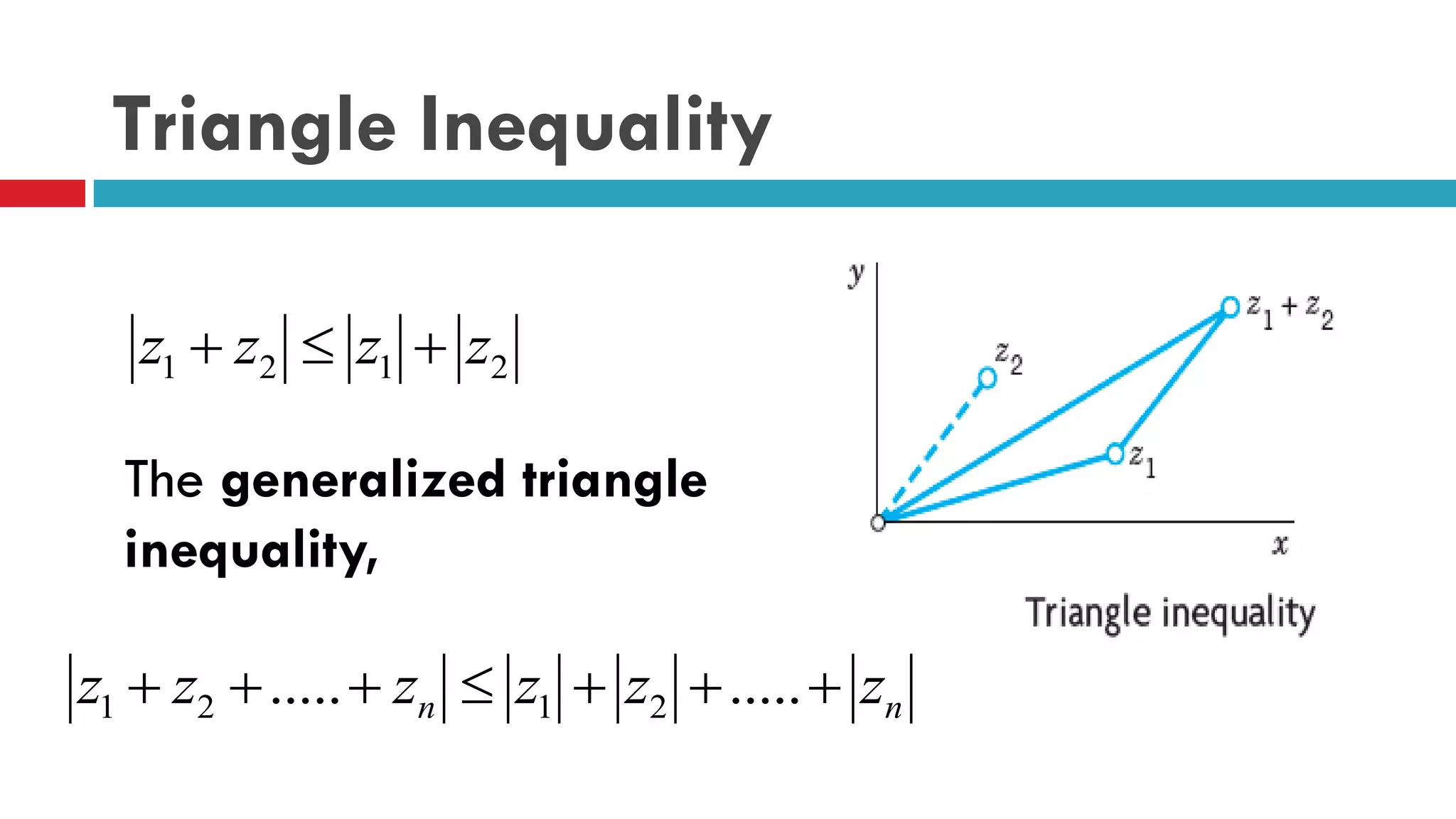
The document discusses complex numbers, their geometric representation, and operations such as addition, subtraction, multiplication, and division. It introduces the polar form of complex numbers and explores concepts such as limits, continuity, and derivatives in complex functions. Additionally, the text covers properties of open and closed sets in the complex plane, as well as analytic functions.
























![Multiplication and Division in Polar Form
Let,
Then ,
the absolute value of a product equals the product of
the absolute values of the factors,
),sin(cos 1111 irz )sin(cos 2222 irz
)]sin()[cos( 21212121 irrzz
2121 zzzz ](https://image.slidesharecdn.com/presentation13final-171227231129/75/Complex-Numbers-and-Functions-Complex-Differentiation-27-2048.jpg)
![Multiplication and Division in Polar Form
the argument of a product equals the sum of the
arguments of the factors,
Division.
2121 argarg)arg( zzzz
)]sin()[cos( 2121
2
1
2
1
i
r
r
z
z](https://image.slidesharecdn.com/presentation13final-171227231129/75/Complex-Numbers-and-Functions-Complex-Differentiation-28-2048.jpg)

![Integer Powers of z
De Moivre’s Formula
If n is an integer,
Then,
),sin(cos ninrz nn
,)]sin(cos[ nn
irz ](https://image.slidesharecdn.com/presentation13final-171227231129/75/Complex-Numbers-and-Functions-Complex-Differentiation-30-2048.jpg)