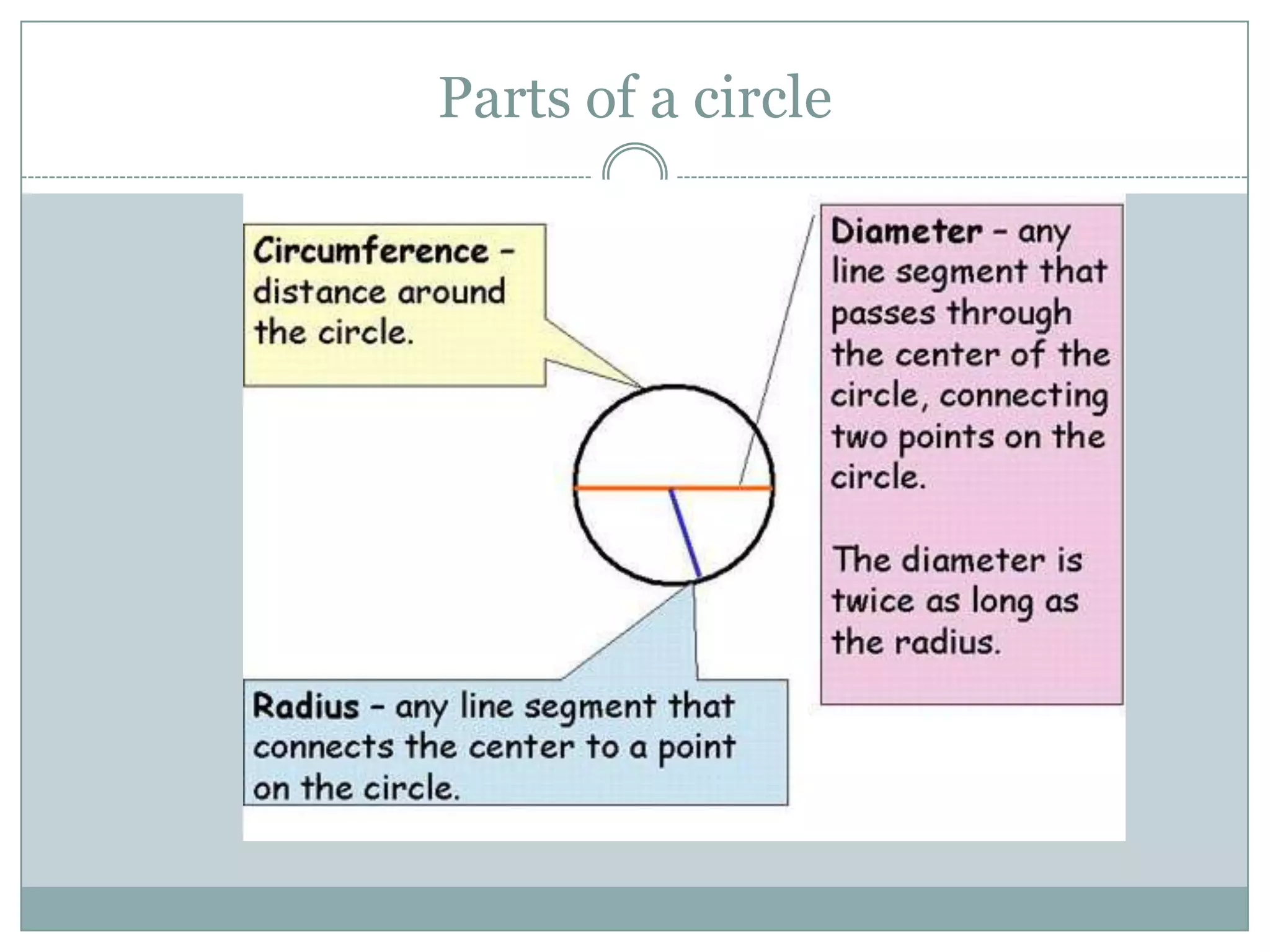
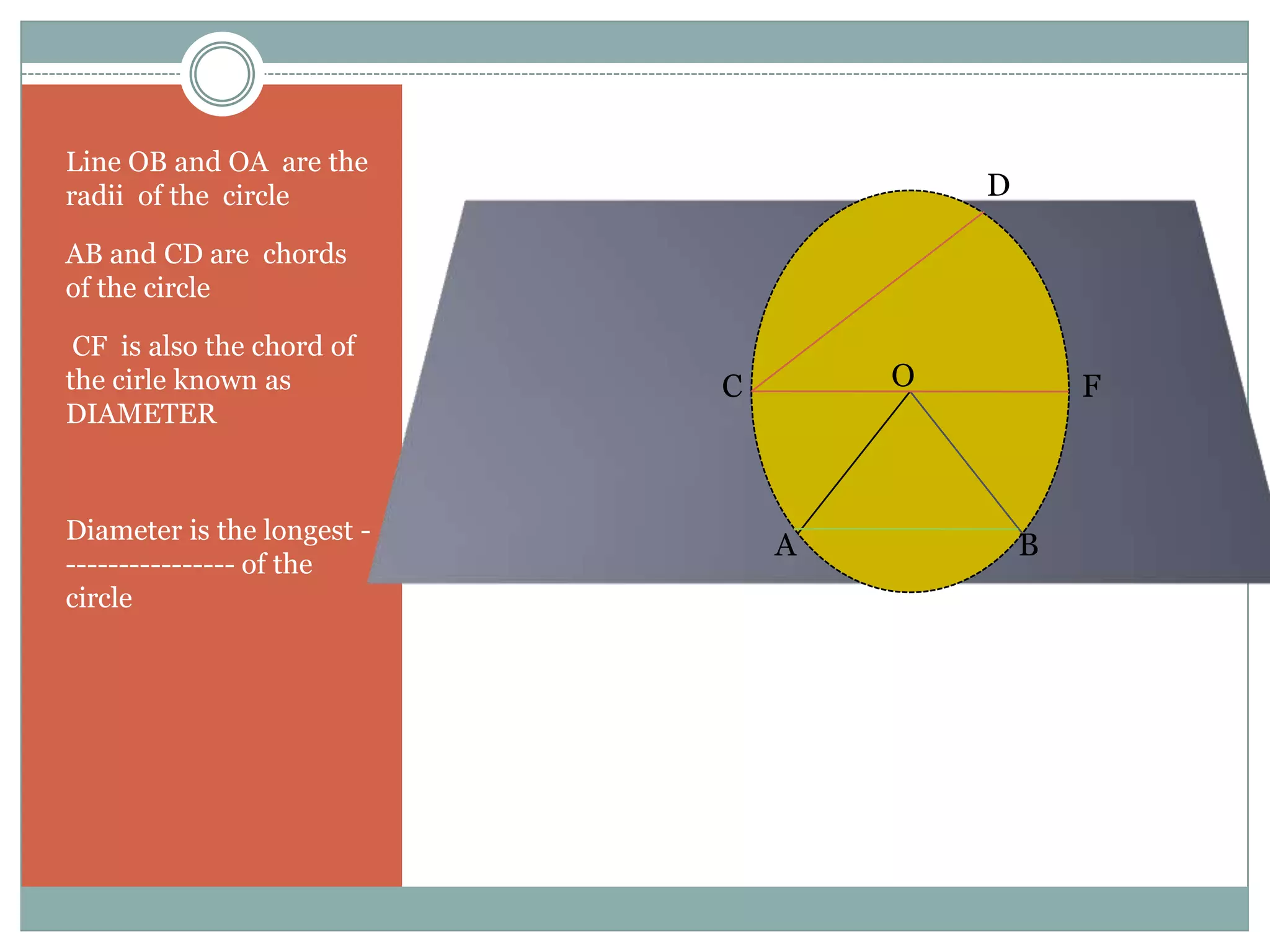
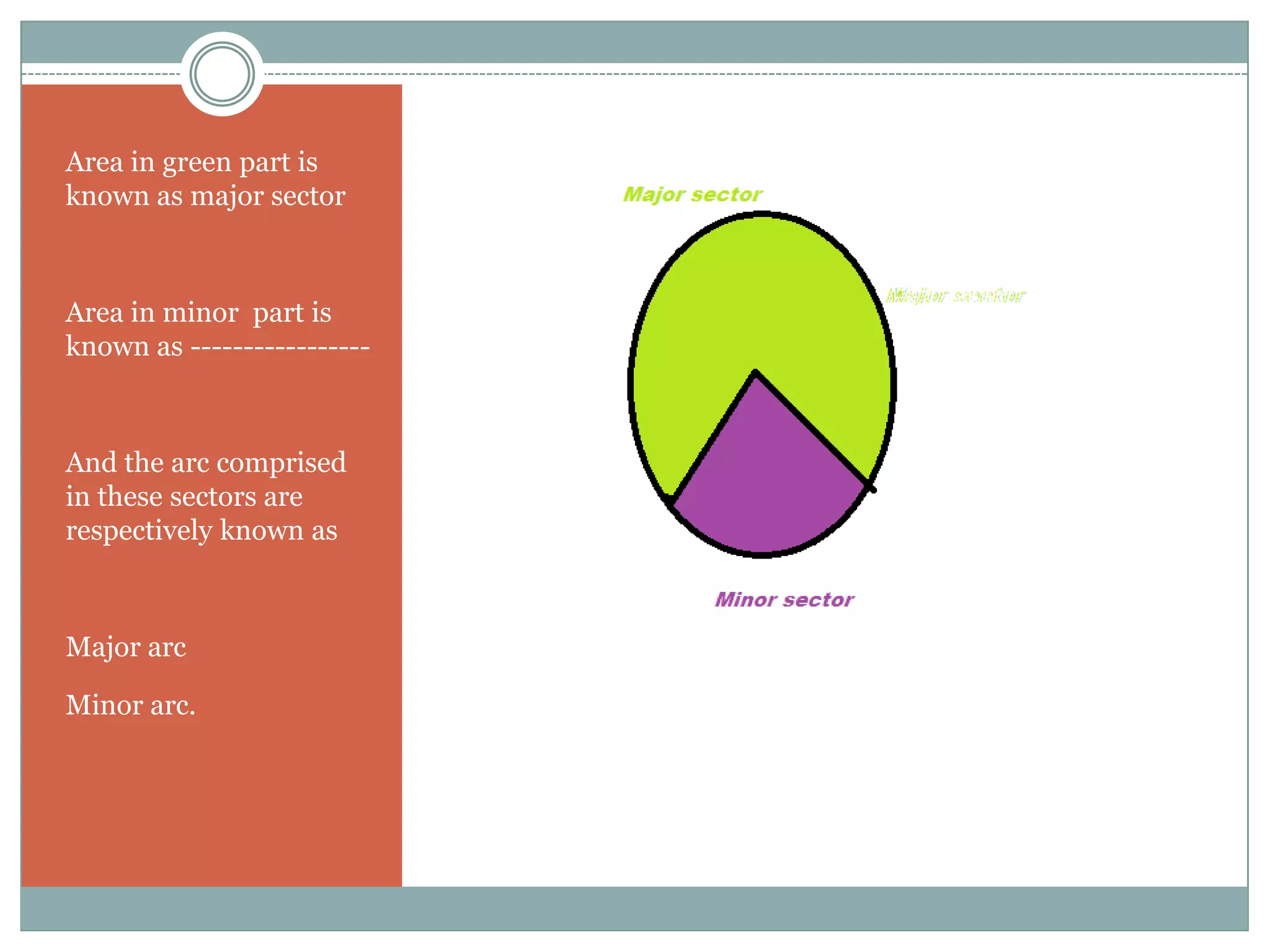
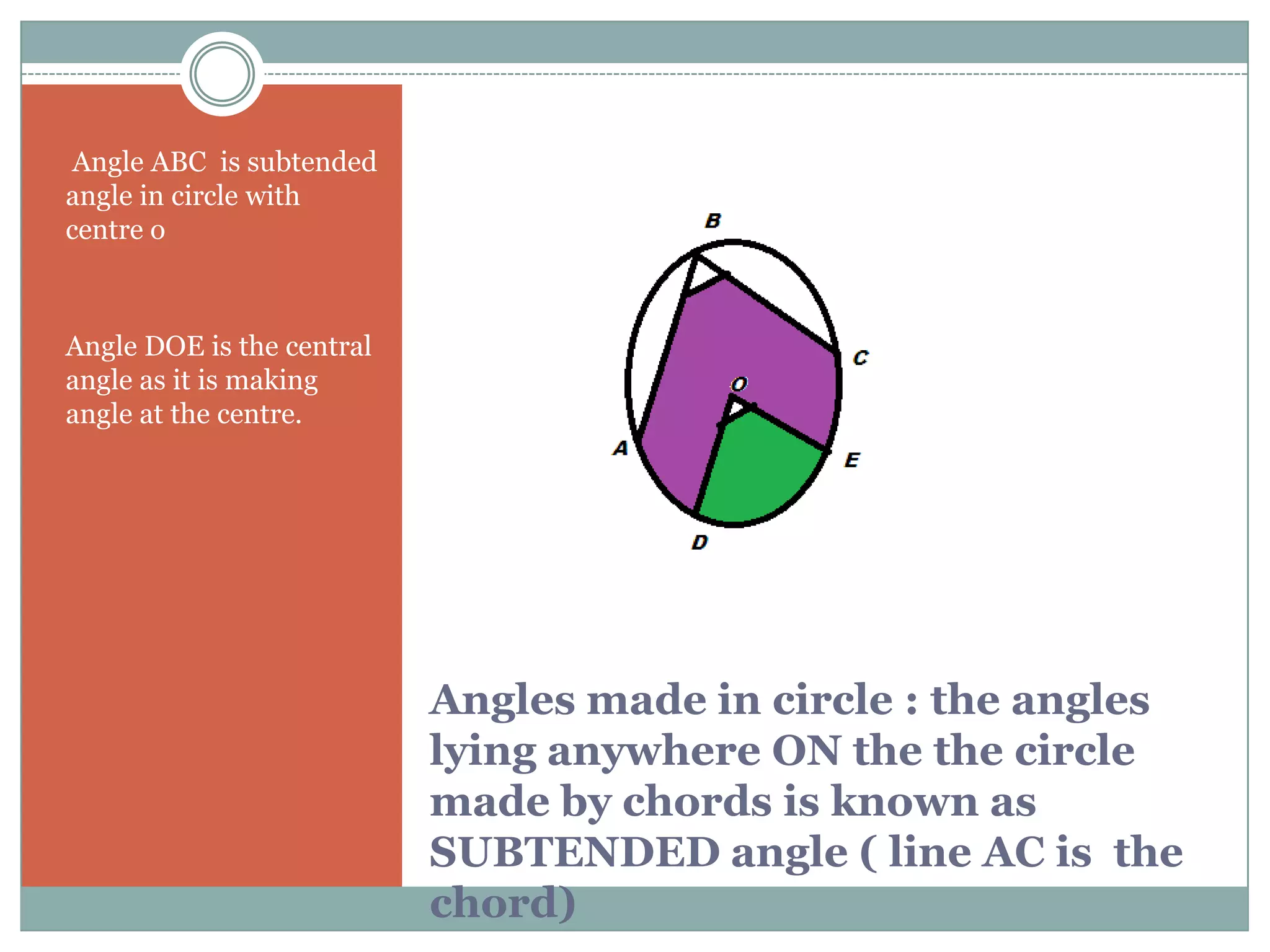
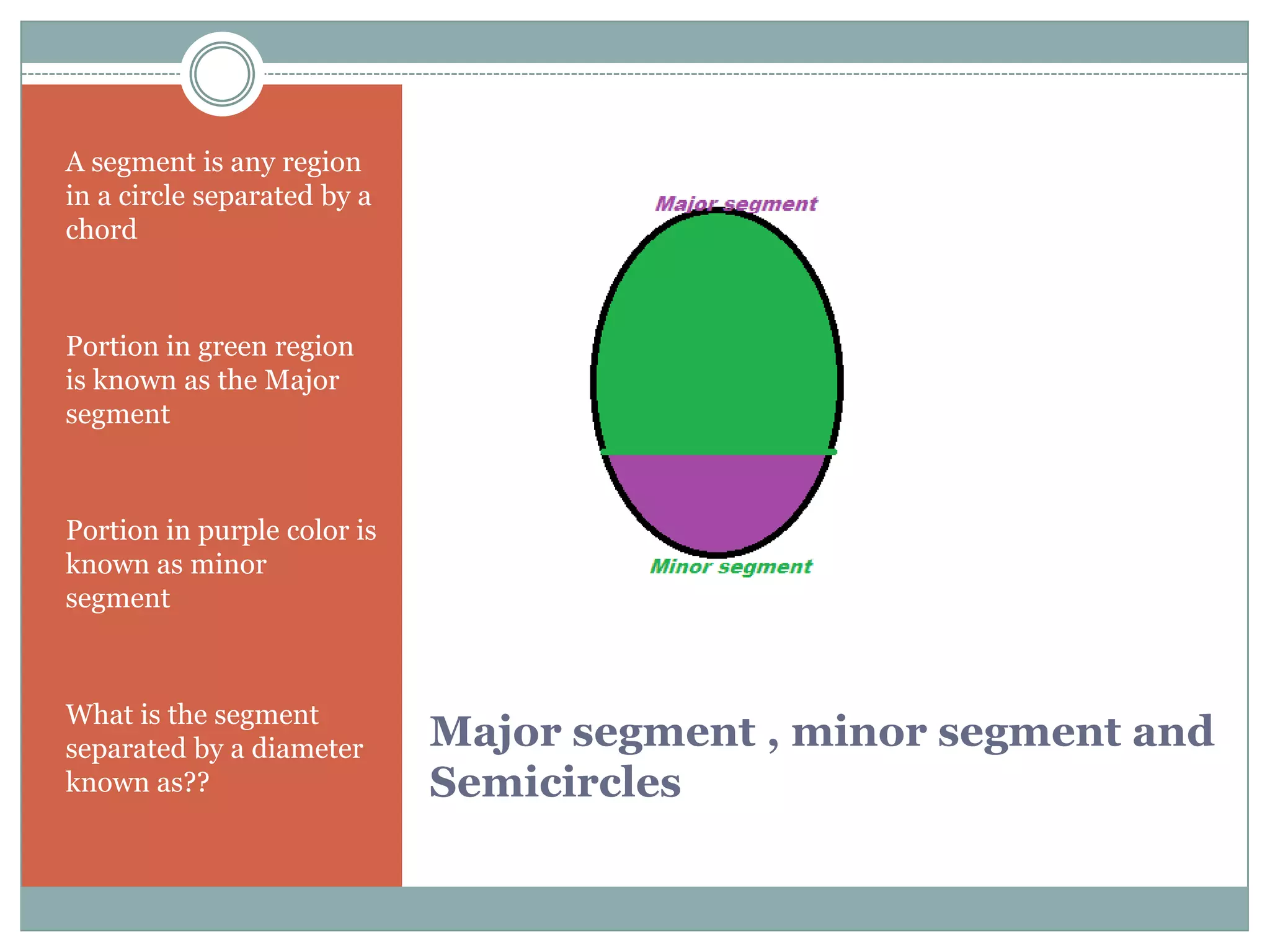
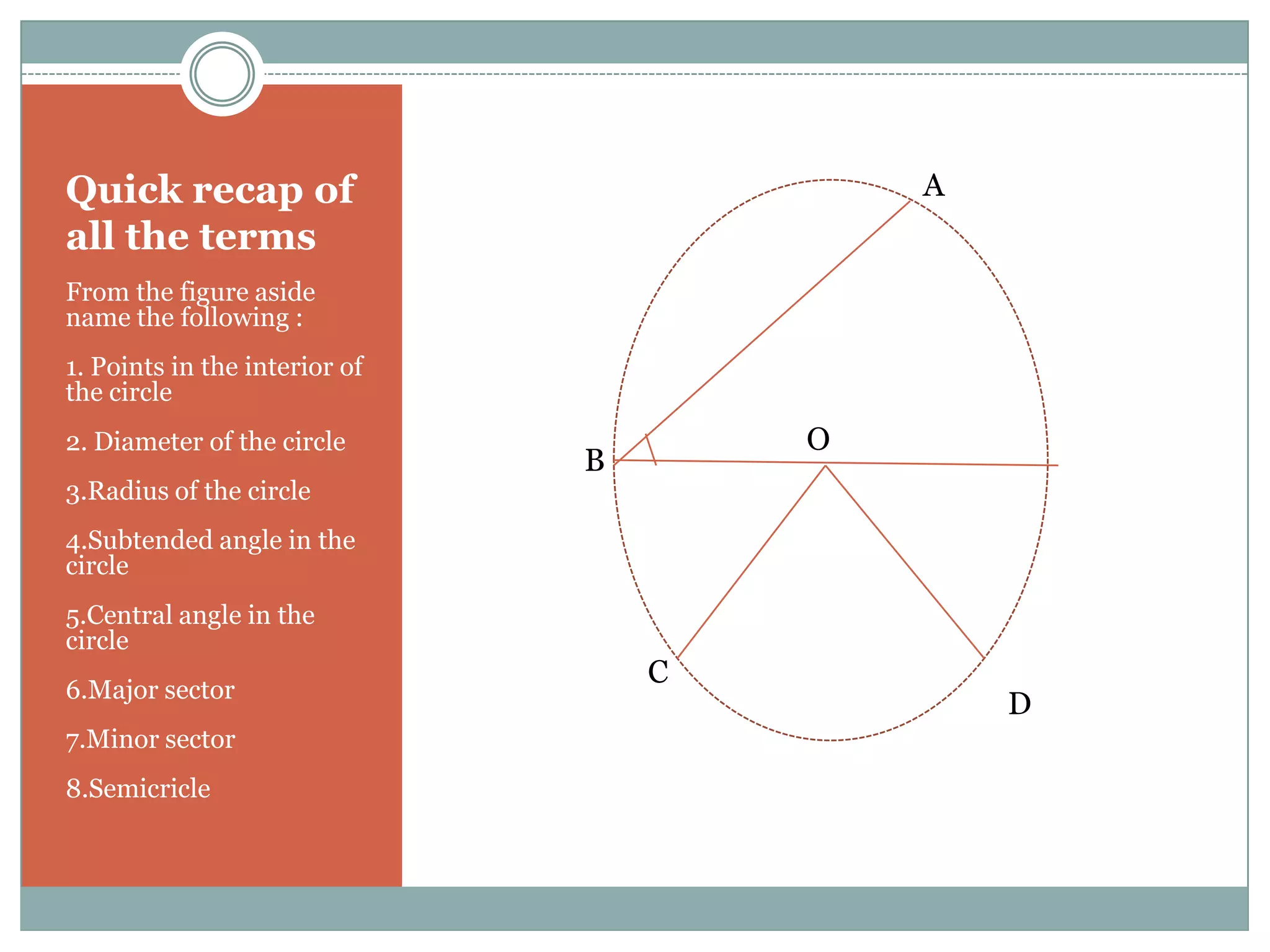
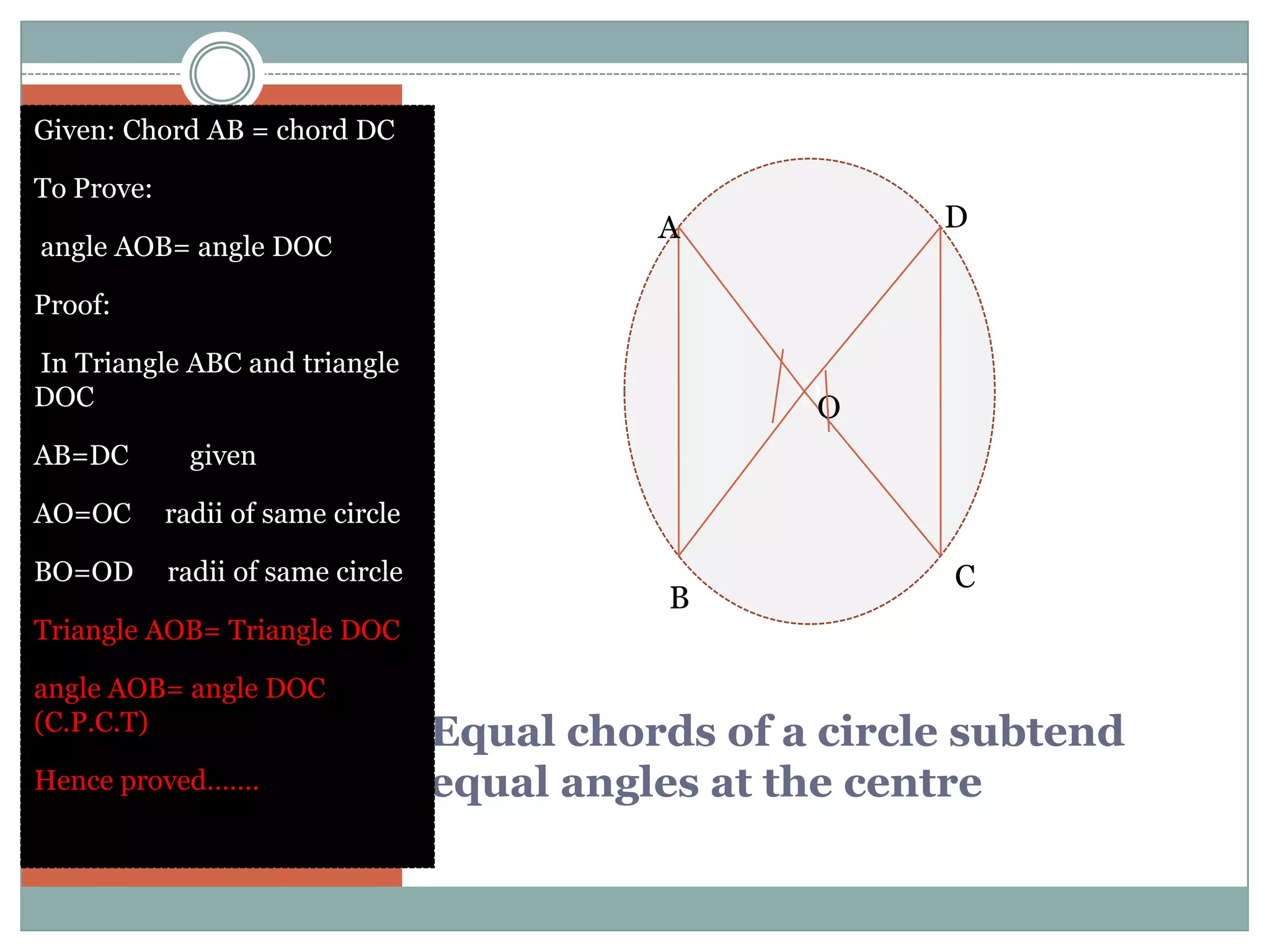
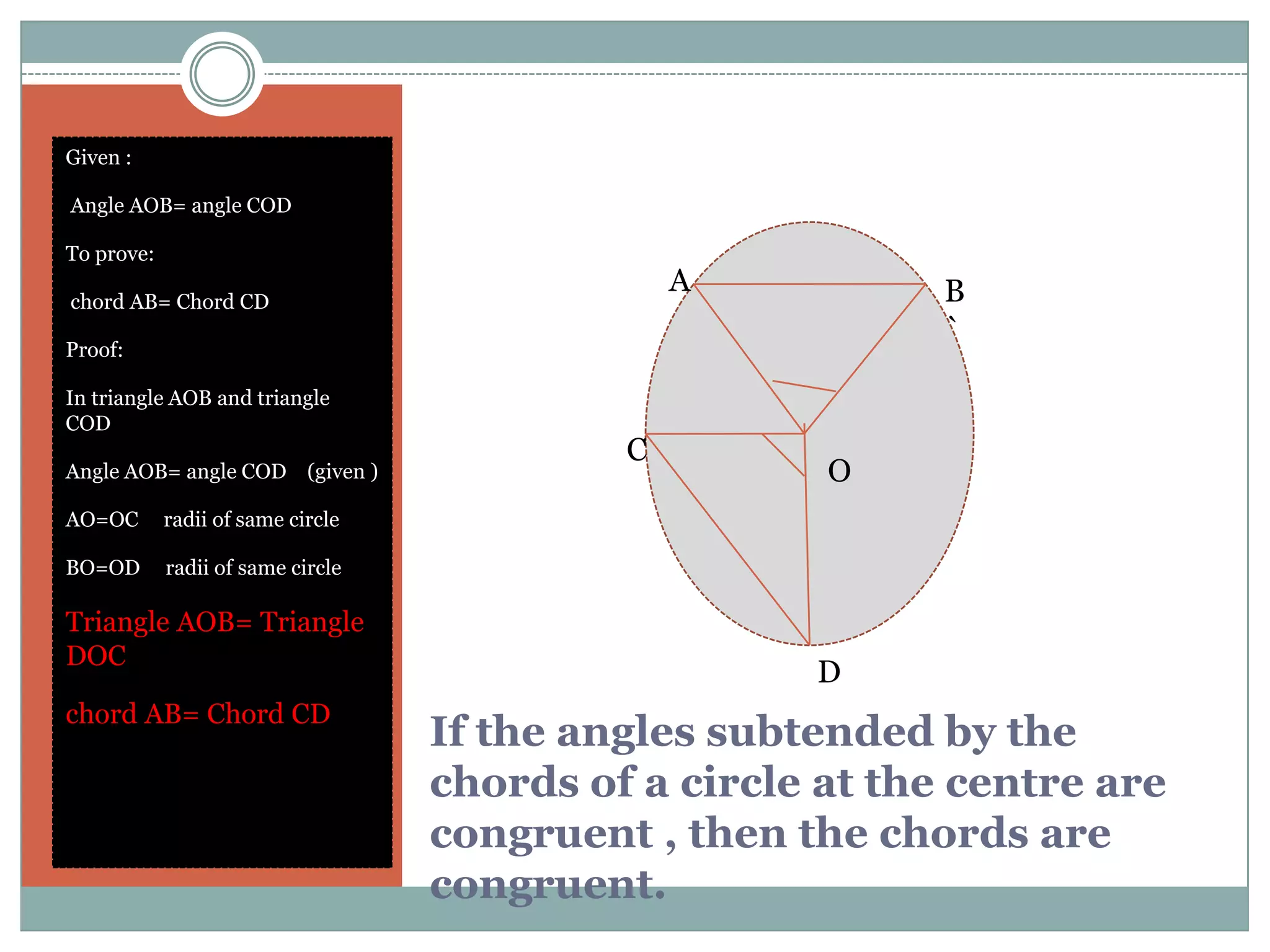
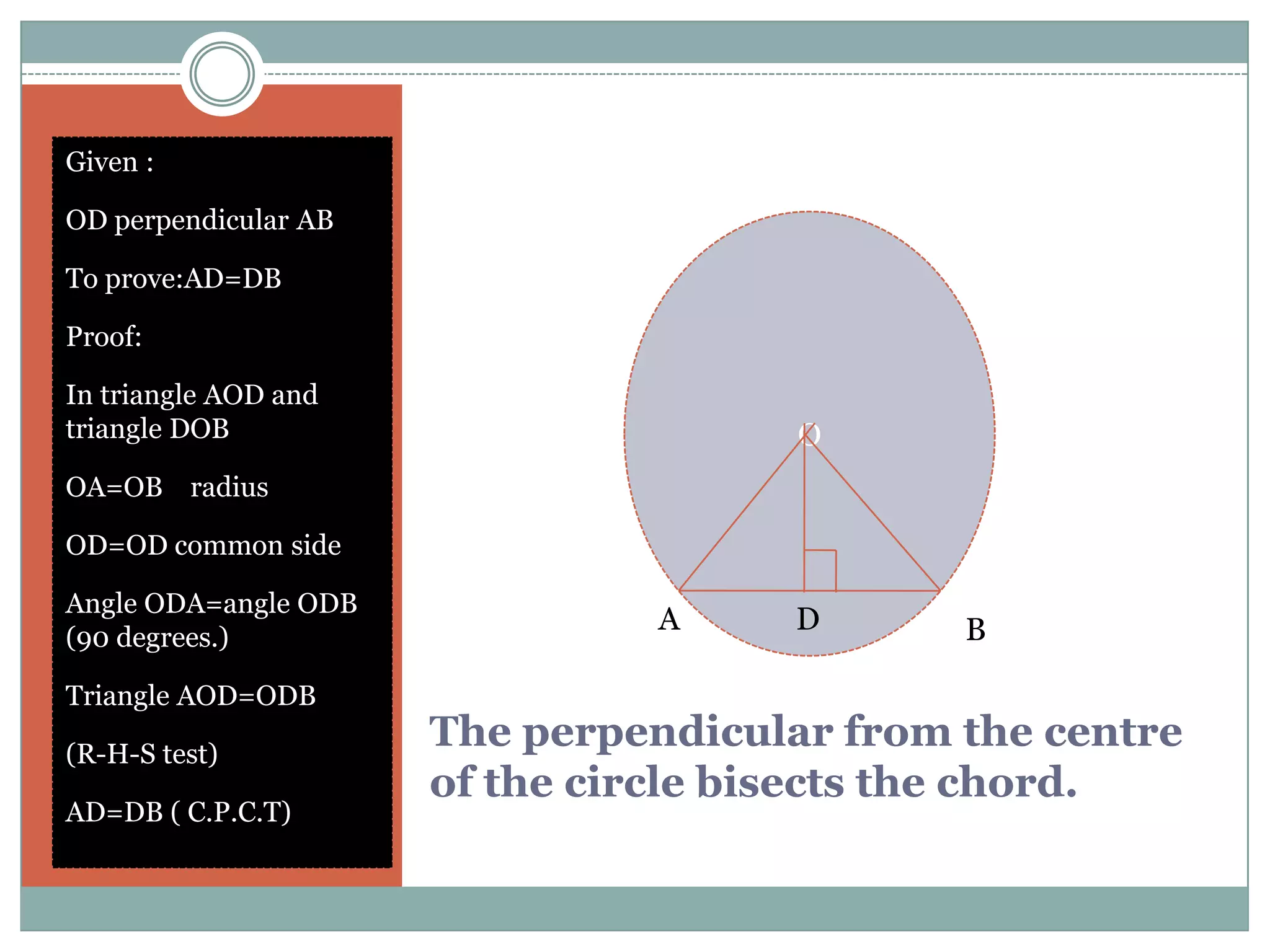
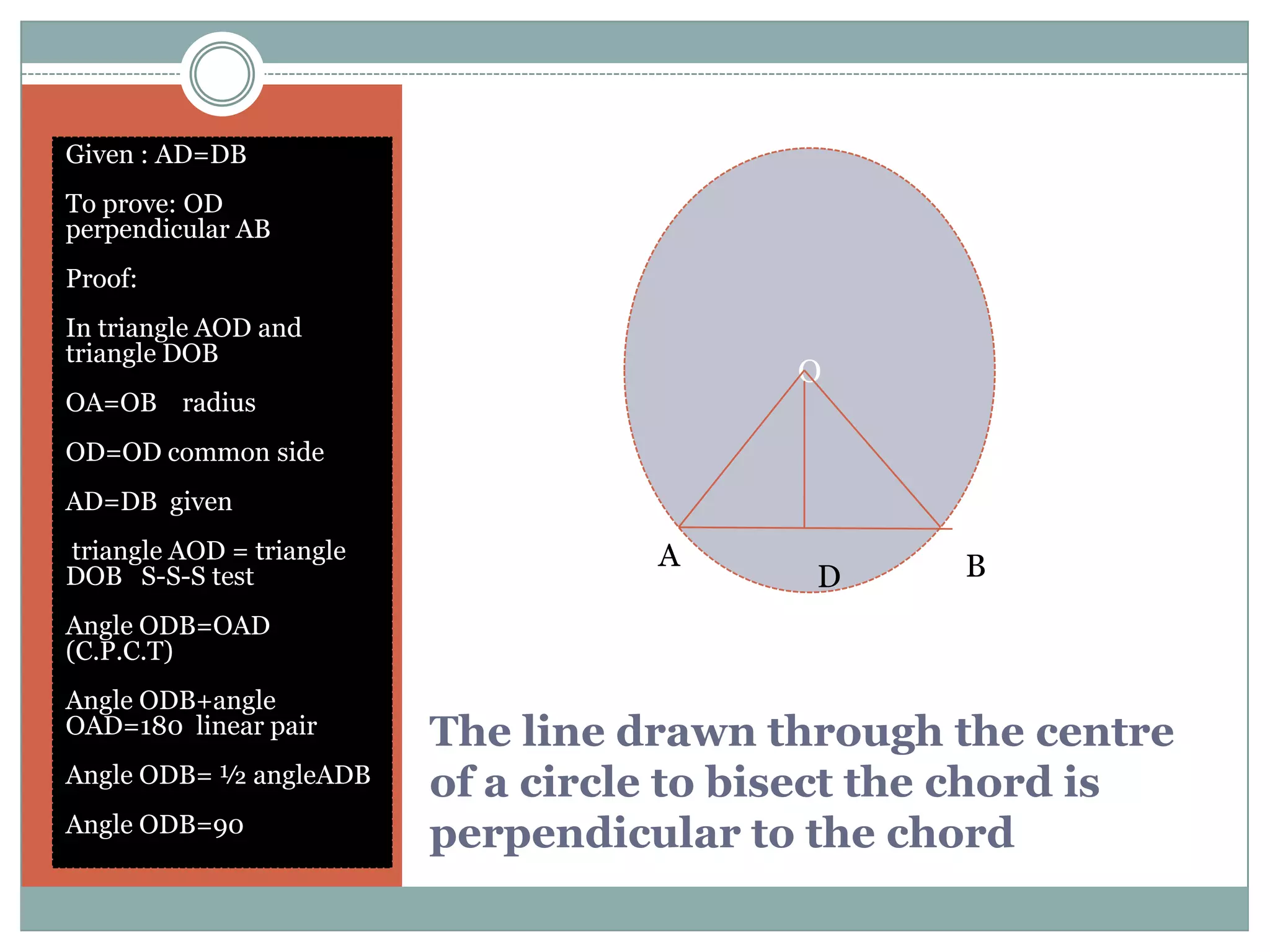
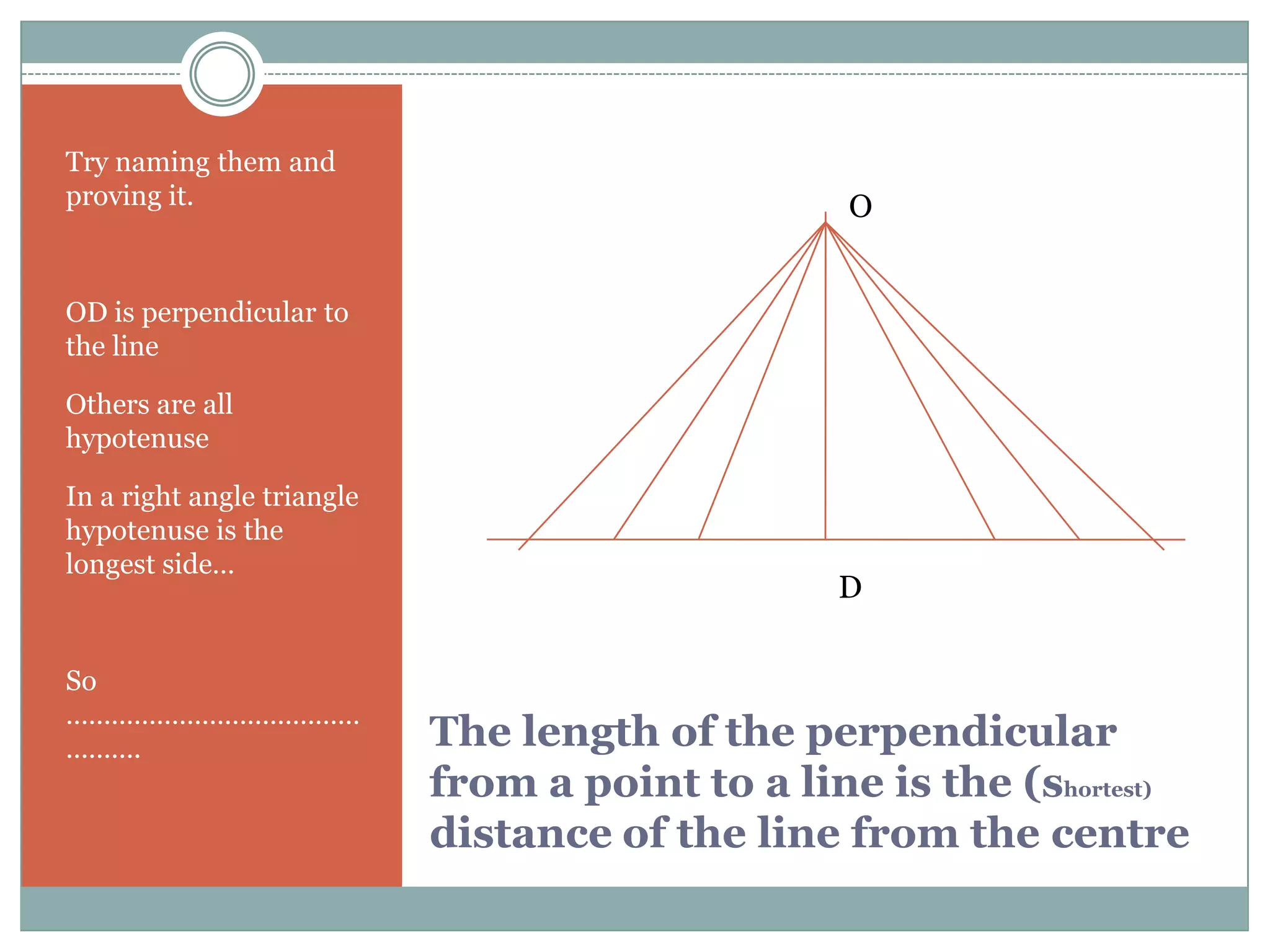
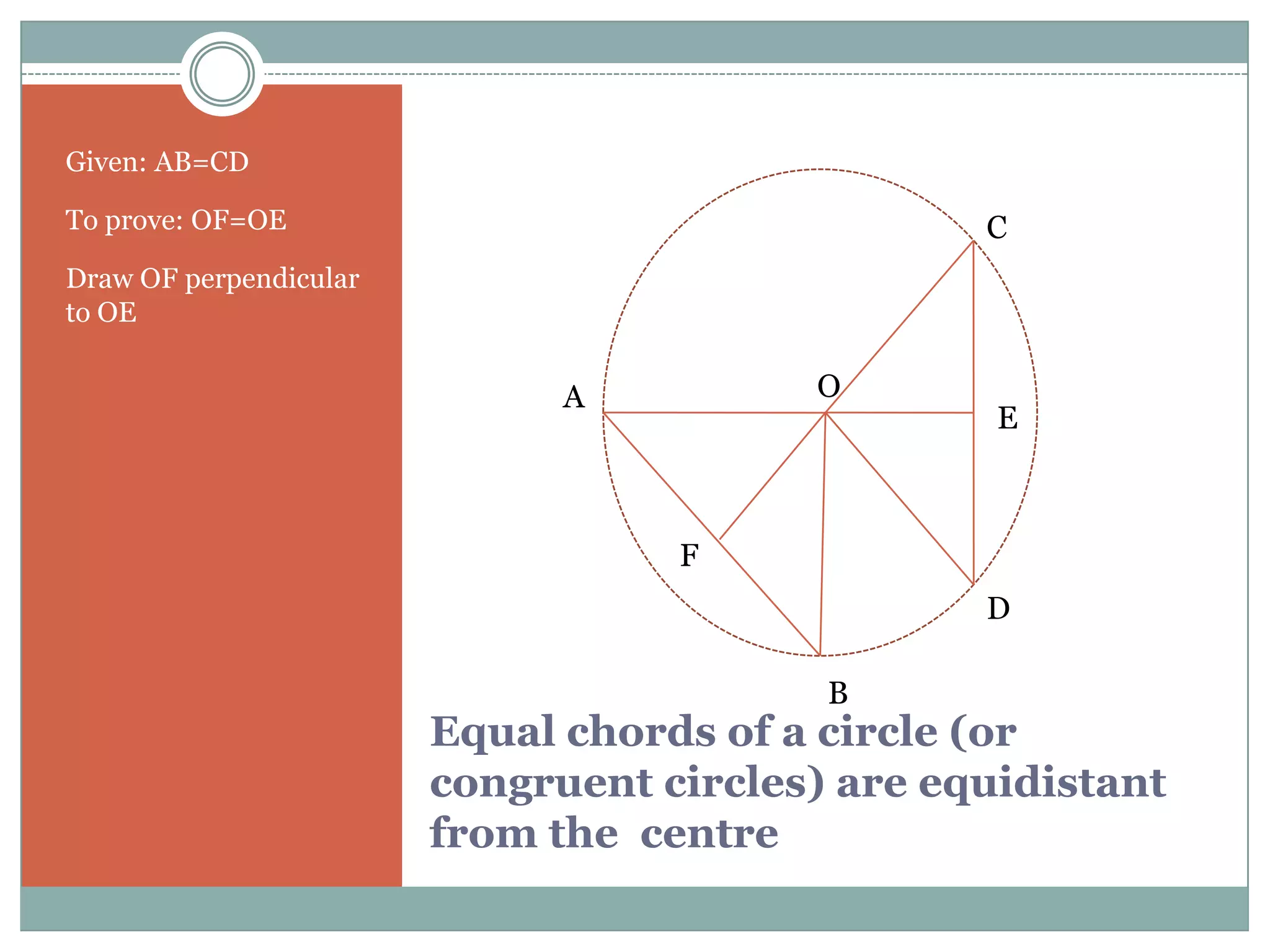
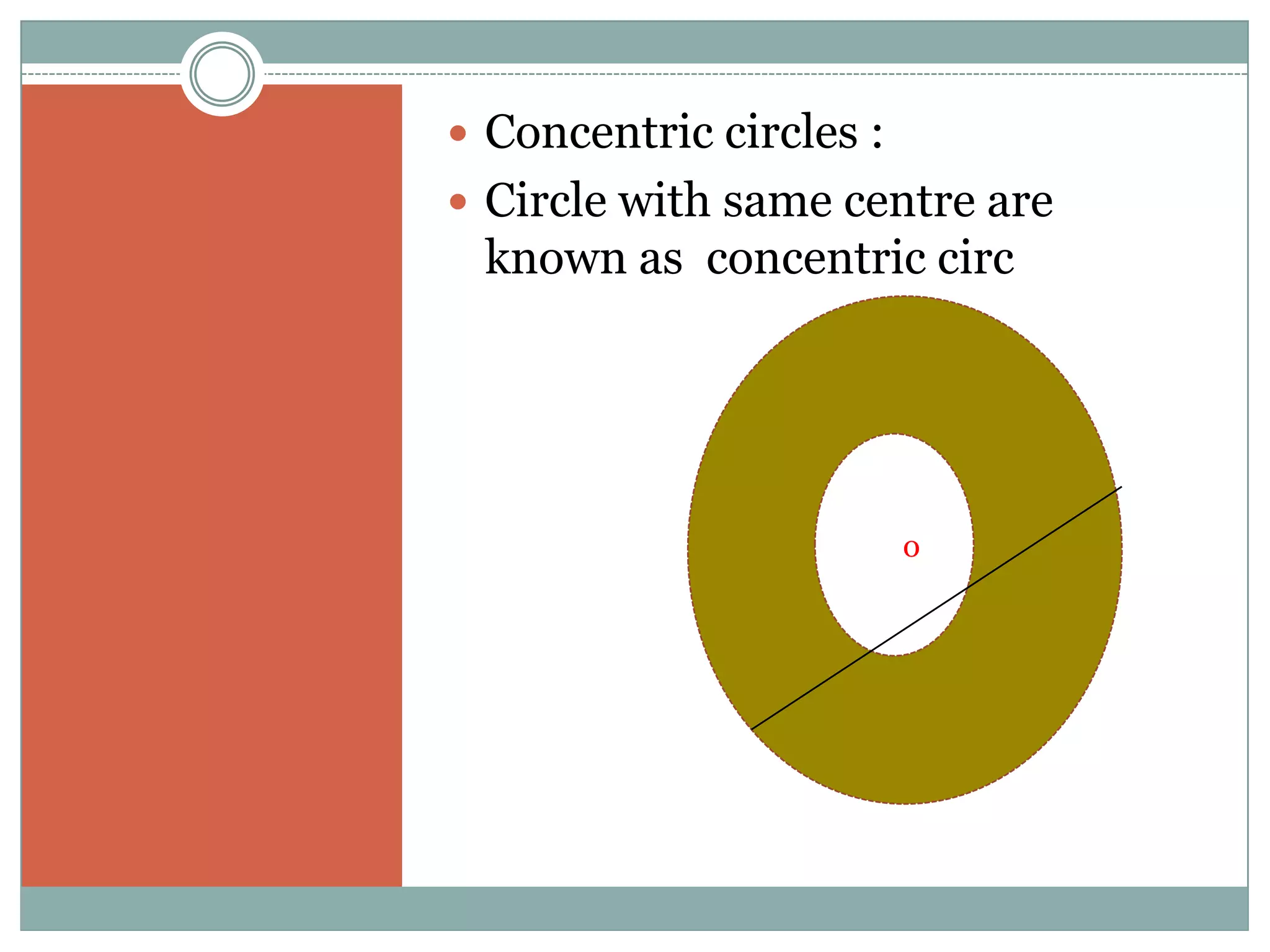
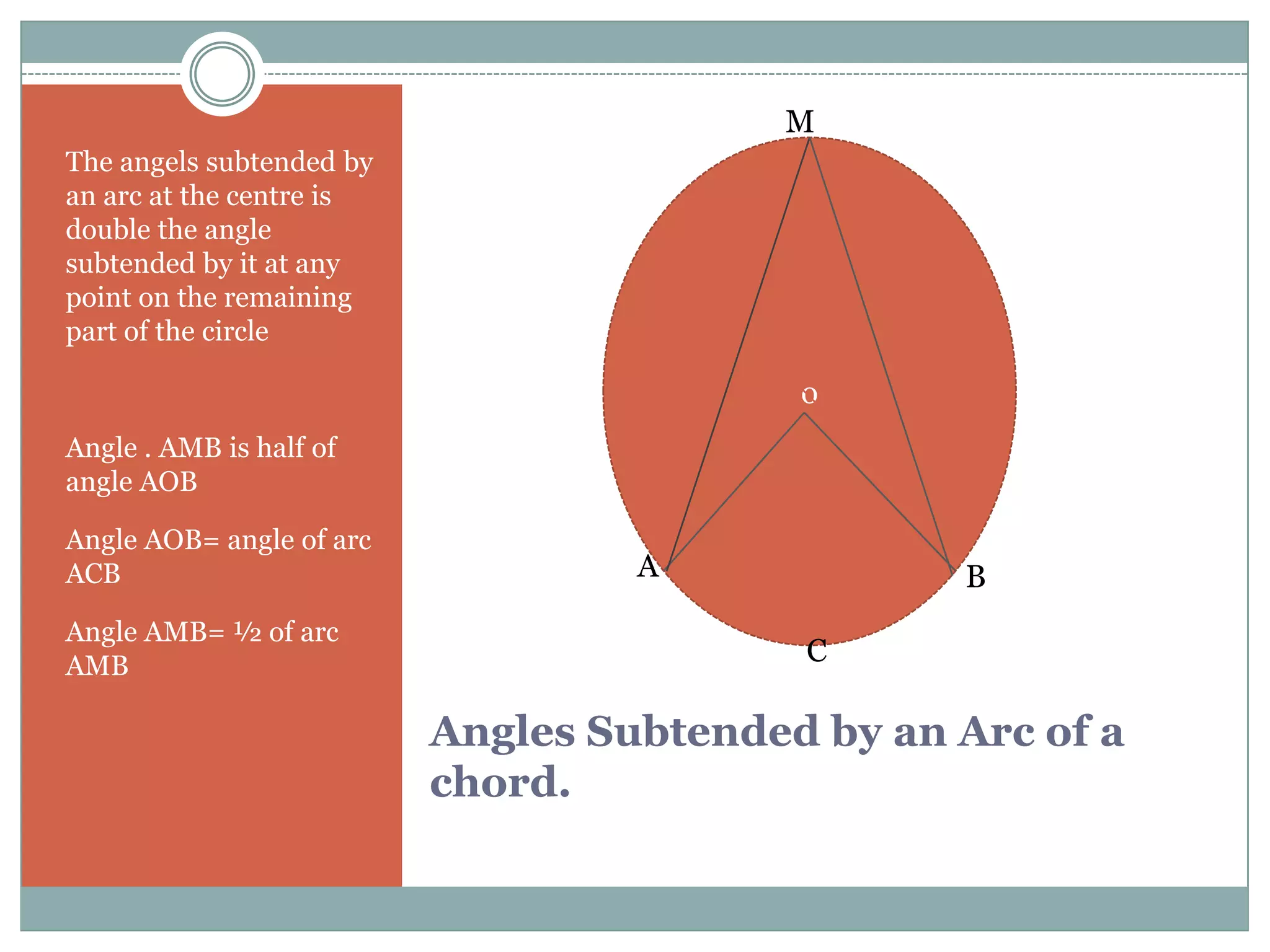
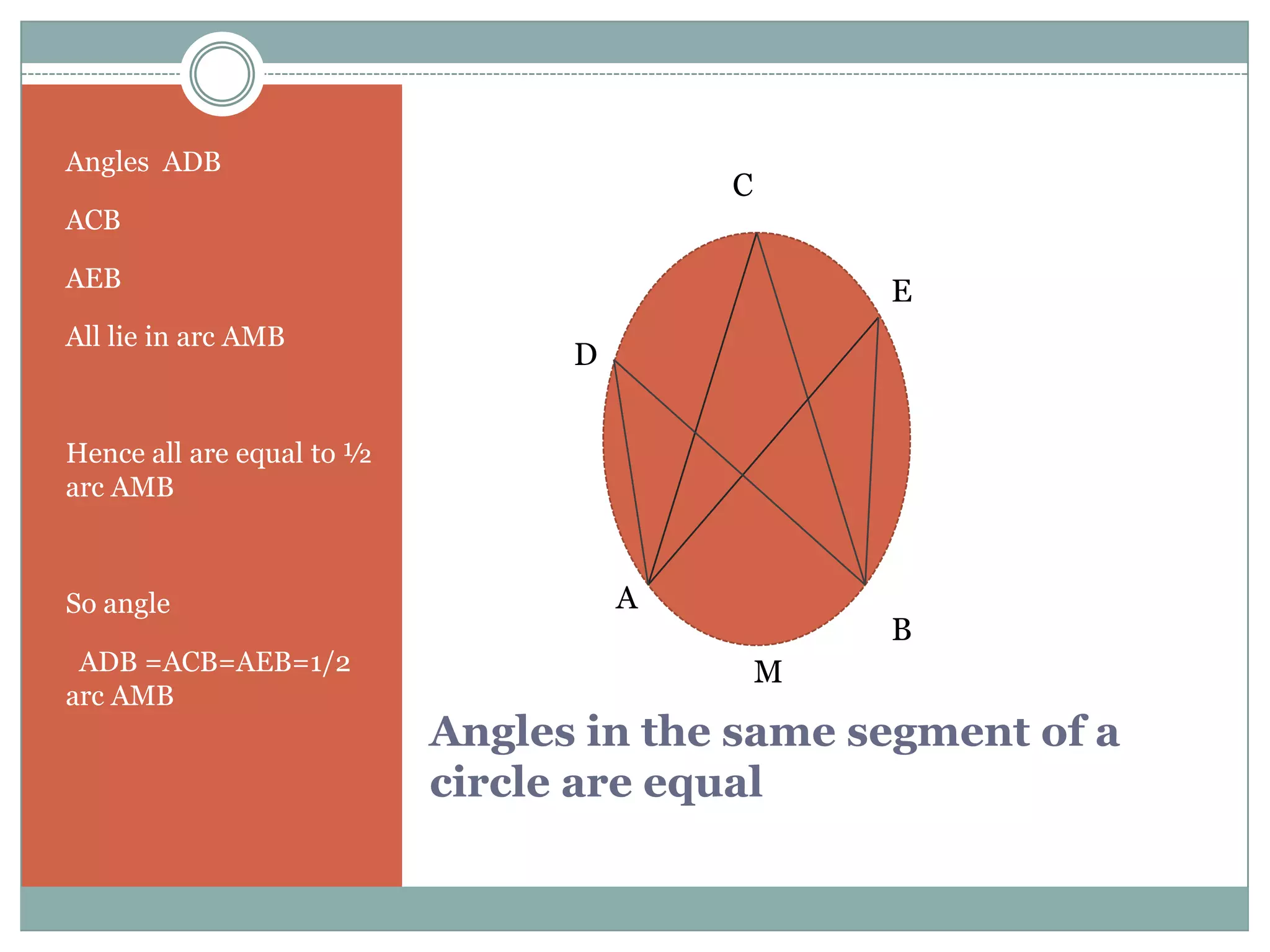
The document defines key terms related to circles such as radius, diameter, chord, arc, sector, segment, and central angle. It also presents several theorems about circles: (1) Equal chords of a circle subtend equal angles at the center; (2) If the angles subtended by the chords of a circle at the centre are congruent, then the chords are congruent; (3) The perpendicular from the centre of the circle bisects the chord. It also defines concentric circles and cyclic quadrilaterals.

1. Know all about a Circle
THE COLLECTION OF ALL THE POINTS IN A
PLANE , WHICH ARE AT A FIXED DISTANCE
FROM A FIXED POINT IN A PLANE, IS
CALLED A CIRCLE

2. Parts of a circle

3. Line OB and OA are the
radii of the circle D
AB and CD are chords
of the circle
CF is also the chord of
the cirle known as C O F
DIAMETER
Diameter is the longest -
A B
---------------- of the
circle

4. Area in green part is
known as major sector
Area in minor part is
known as -----------------
And the arc comprised
in these sectors are
respectively known as
Major arc
Minor arc.

5. Angle ABC is subtended
angle in circle with
centre o
Angle DOE is the central
angle as it is making
angle at the centre.
Angles made in circle : the angles
lying anywhere ON the the circle
made by chords is known as
SUBTENDED angle ( line AC is the
chord)

6. A segment is any region
in a circle separated by a
chord
Portion in green region
is known as the Major
segment
Portion in purple color is
known as minor
segment
What is the segment
separated by a diameter Major segment , minor segment and
known as?? Semicircles

7. Quick recap of A
all the terms
From the figure aside
name the following :
1. Points in the interior of
the circle
2. Diameter of the circle O
B
3.Radius of the circle
4.Subtended angle in the
circle
5.Central angle in the
circle
C
6.Major sector
D
7.Minor sector
8.Semicricle

8. Equal chords of a circle subtend equal angles at
the centre

9. Given: Chord AB = chord DC
To Prove:
A D
angle AOB= angle DOC
Proof:
In Triangle ABC and triangle
DOC OO
AB=DC given
AO=OC radii of same circle
BO=OD radii of same circle C
B
Triangle AOB= Triangle DOC
angle AOB= angle DOC
(C.P.C.T)
Equal chords of a circle subtend
Hence proved……. equal angles at the centre

10. Given :
Angle AOB= angle COD
To prove:
A B
chord AB= Chord CD
`
Proof:
In triangle AOB and triangle
COD
C
Angle AOB= angle COD (given ) O
AO=OC radii of same circle
BO=OD radii of same circle
Triangle AOB= Triangle
DOC
D
chord AB= Chord CD
If the angles subtended by the
chords of a circle at the centre are
congruent , then the chords are
congruent.

11. Given :
OD perpendicular AB
To prove:AD=DB
Proof:
In triangle AOD and
triangle DOB O
OA=OB radius
OD=OD common side
Angle ODA=angle ODB
A D B
(90 degrees.)
Triangle AOD=ODB
(R-H-S test)
The perpendicular from the centre
of the circle bisects the chord.
AD=DB ( C.P.C.T)

12. Given : AD=DB
To prove: OD
perpendicular AB
Proof:
In triangle AOD and
triangle DOB
O
OA=OB radius
OD=OD common side
AD=DB given
triangle AOD = triangle A
DOB S-S-S test D B
Angle ODB=OAD
(C.P.C.T)
Angle ODB+angle
OAD=180 linear pair The line drawn through the centre
Angle ODB= ½ angleADB of a circle to bisect the chord is
Angle ODB=90
perpendicular to the chord

13. Circle through 1,2,3, points
 On a sheet of paper try drawing circle through one
point
 Two points
 Three points
 What do you see?

14. Answers
 Many circles can be drawn from one point
 Many circles can be drawn from two points
 But one and only one circle can be drawn from three
points.

15. Try naming them and
proving it. O
OD is perpendicular to
the line
Others are all
hypotenuse
In a right angle triangle
hypotenuse is the
longest side…
D
So
…………………………………
………. The length of the perpendicular
from a point to a line is the (shortest)
distance of the line from the centre

16. Given: AB=CD
To prove: OF=OE C
Draw OF perpendicular
to OE
A O
OOO E
F
D
B
Equal chords of a circle (or
congruent circles) are equidistant
from the centre

17. Pick statements in proper order to prove the
theorem and match the reasons
 Statements  Reasons
 AF=FB  Radii of same circle
 AF=1/2AB  C.P.C.T
 CE=ED  Given
 CE=1/2CD  Radii of same circle
 CE=AF  S-S-S test
 Chord AF=chord CE  S-A-S test
 OA =OC  Each 90 degrees
 OB=OD
 In triangles AOF and OCE
 Triangles congruent by
 Angle F= Angle E
 OF=OE

18.  Chords Equidistant from the
centre of a circle are equal in
length
 (converse of the earlier theorem)
 Try proving this…………………..
 Have fun

19.  Concentric circles :
 Circle with same centre are
known as concentric circ
ooo

20. M
The angels subtended by
an arc at the centre is
double the angle
subtended by it at any
point on the remaining
part of the circle
o
Angle . AMB is half of
angle AOB
Angle AOB= angle of arc
ACB A B
Angle AMB= ½ of arc
AMB C
Angles Subtended by an Arc of a
chord.

21. Angles ADB
C
ACB
AEB E
All lie in arc AMB
D
Hence all are equal to ½
arc AMB
So angle A
B
ADB =ACB=AEB=1/2 M
arc AMB
Angles in the same segment of a
circle are equal

22. Cyclic
Quadrilaterals
A Quadrilateral whose
4 corners are on sides of
the circle is known as
cyclic Quadrilateral

23. Properties of  1. the sum of either pair of
Cyclic opposite angles of a cyclic
Quadrilateral quadrilateral is 180 degrees
 If the sum of opposite angles of a
quadrilateral is 180 degrees its
cyclic quadrilateral.