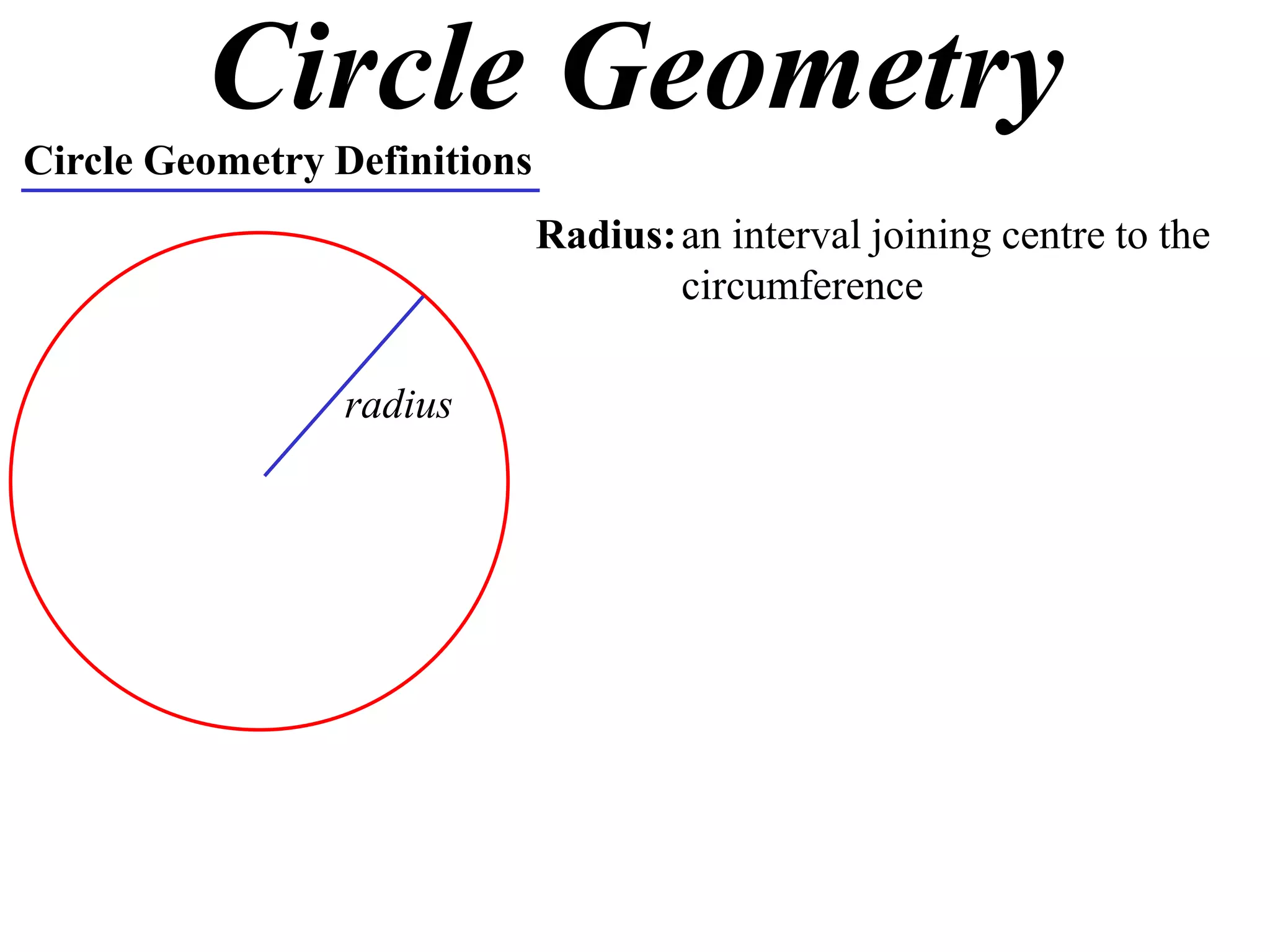
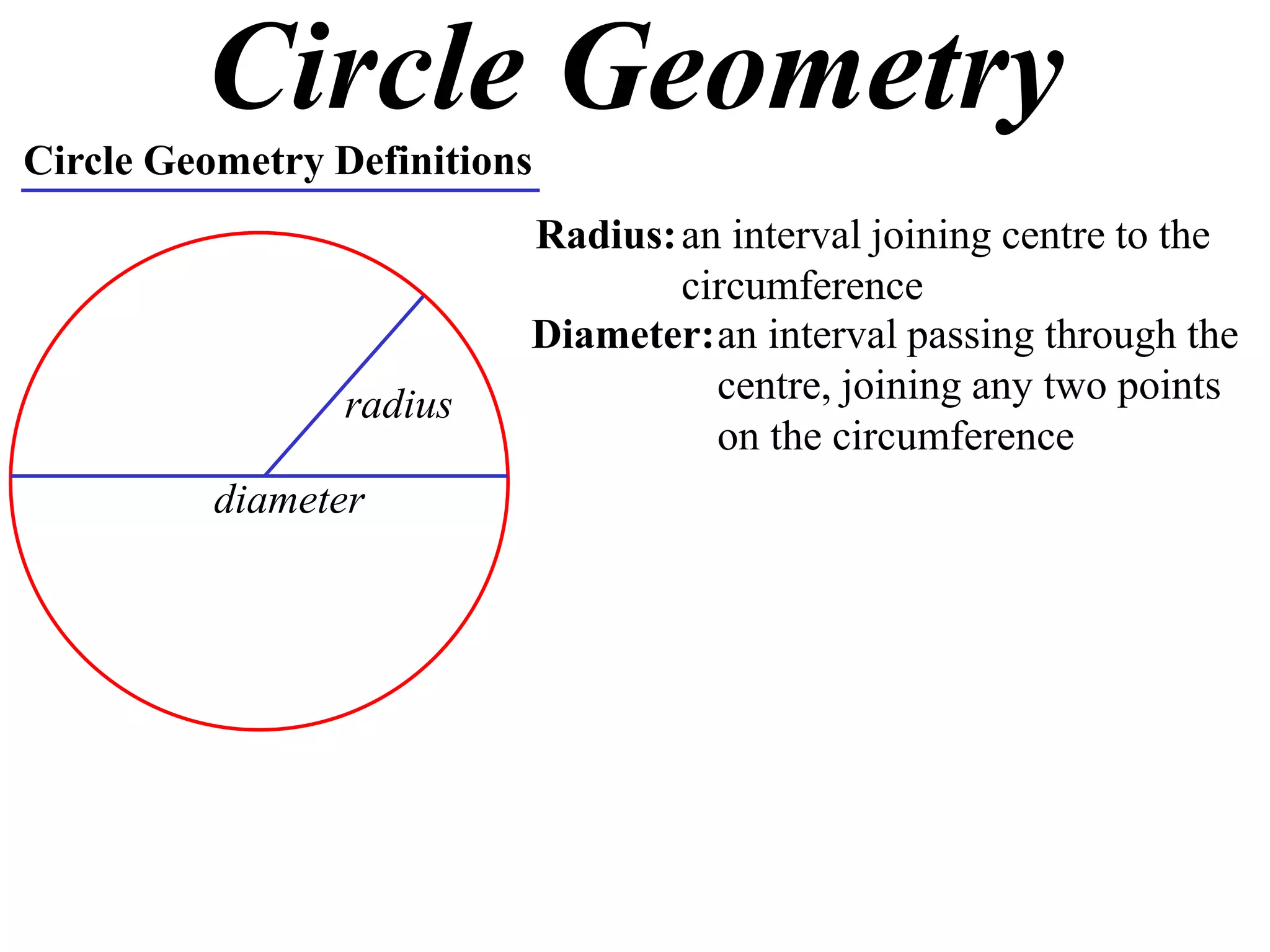
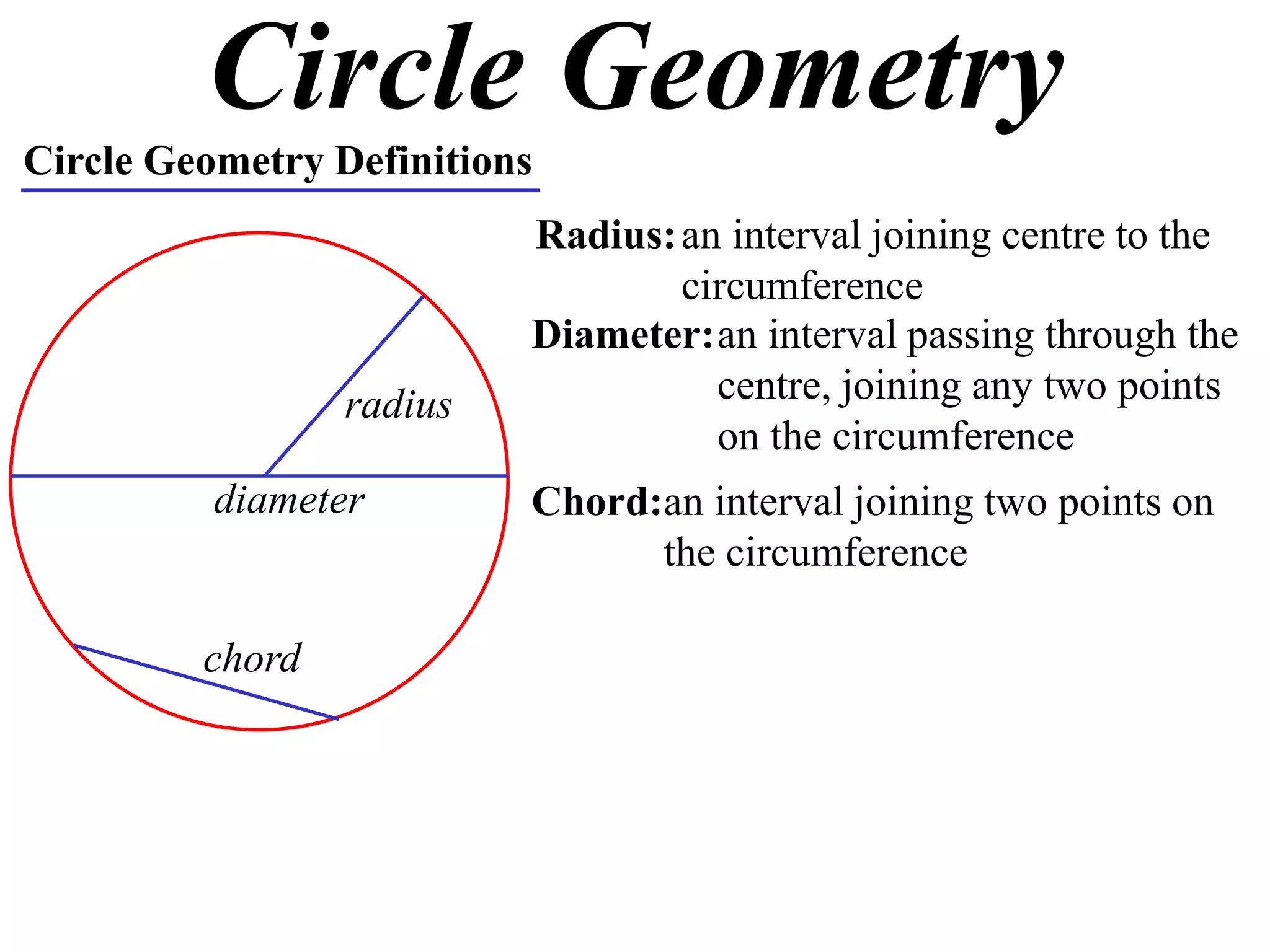
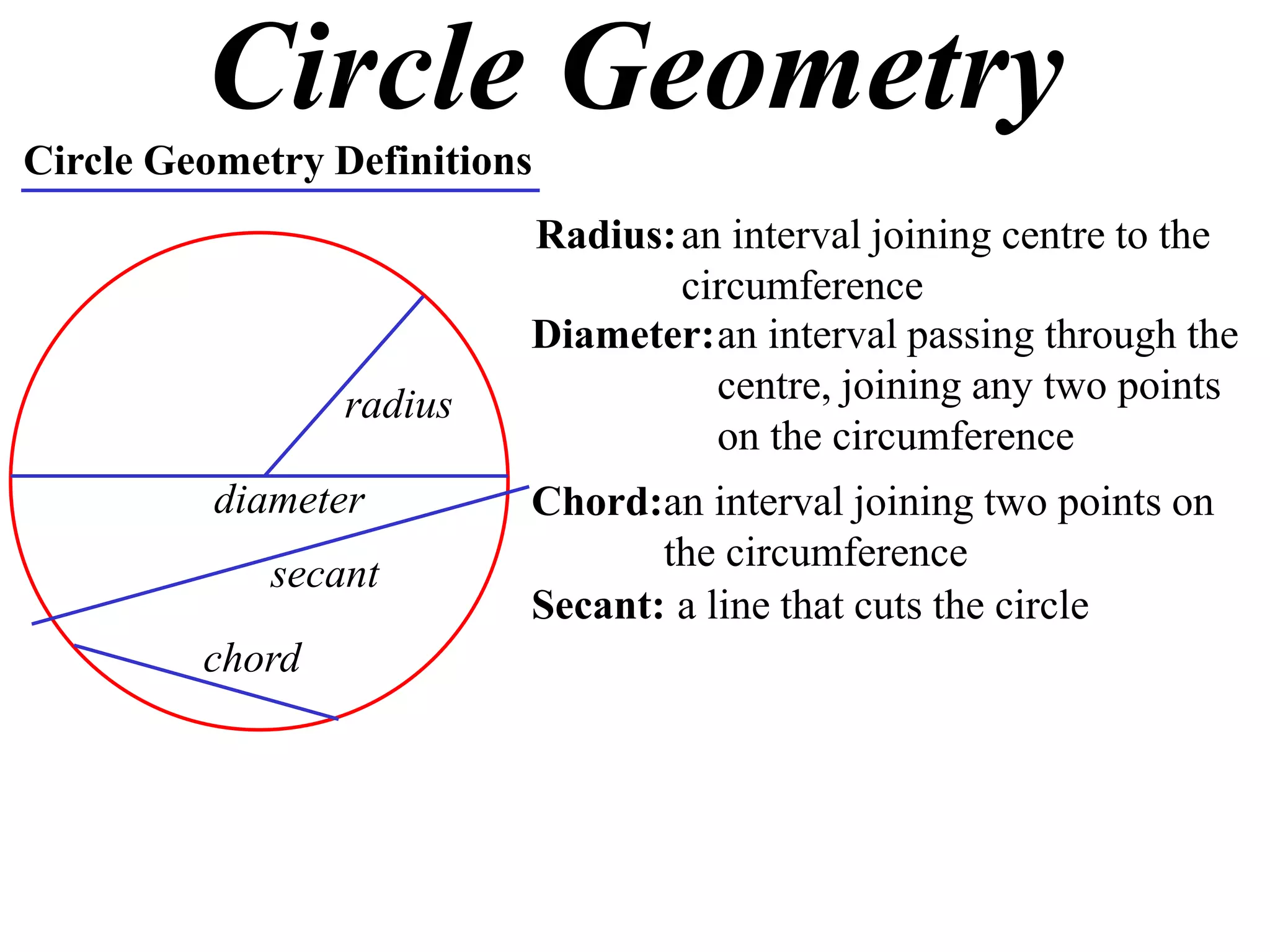
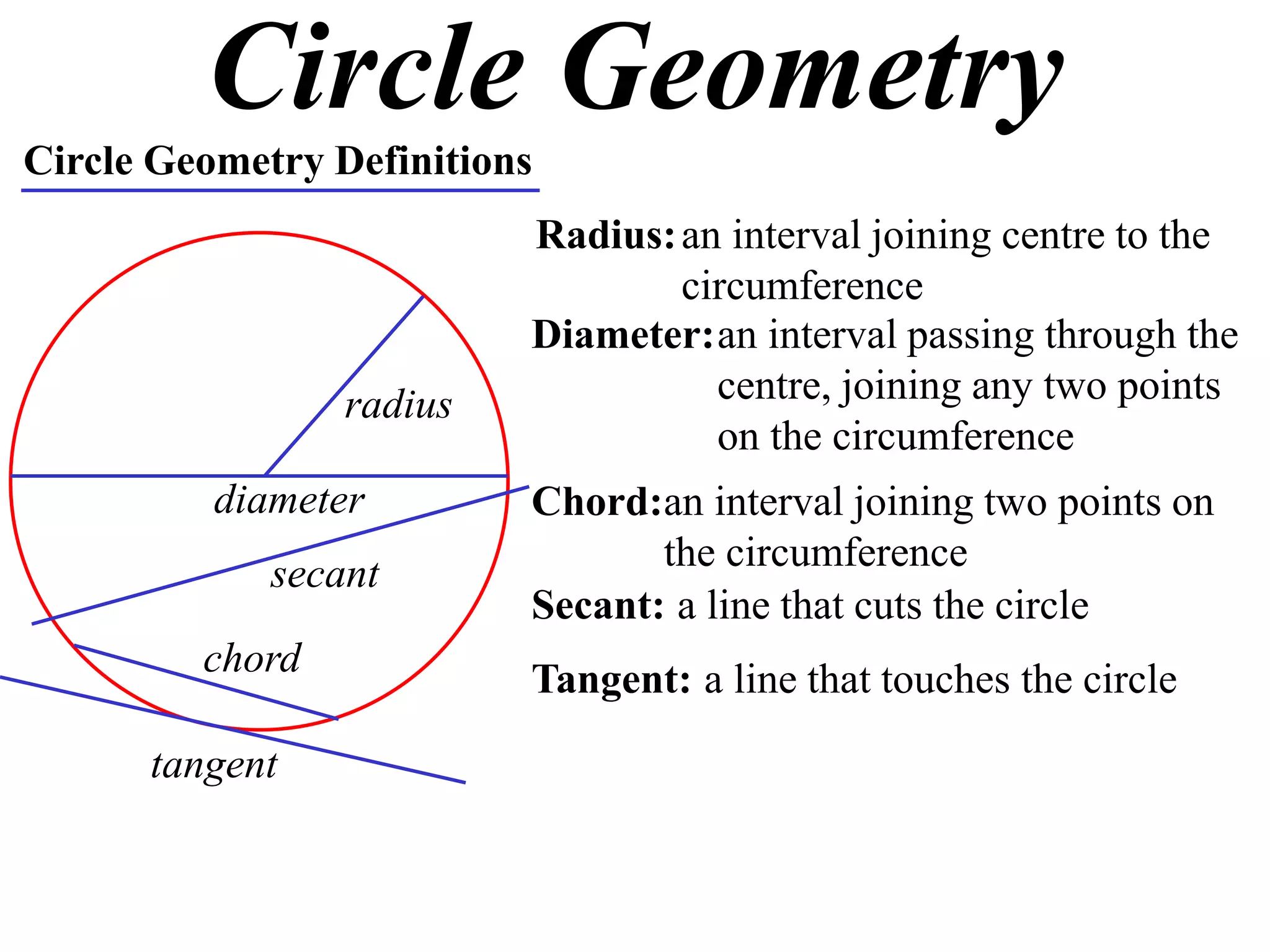
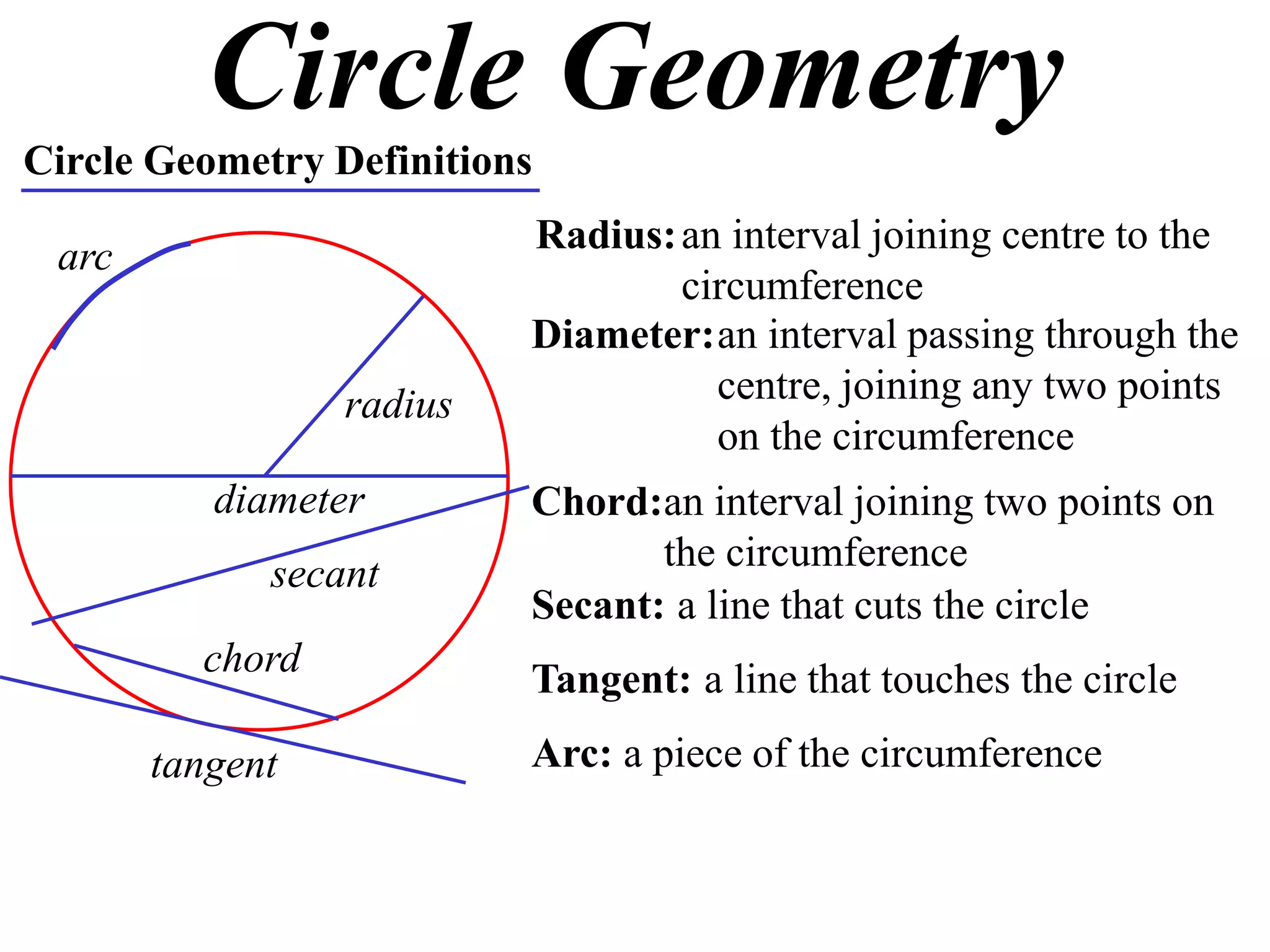
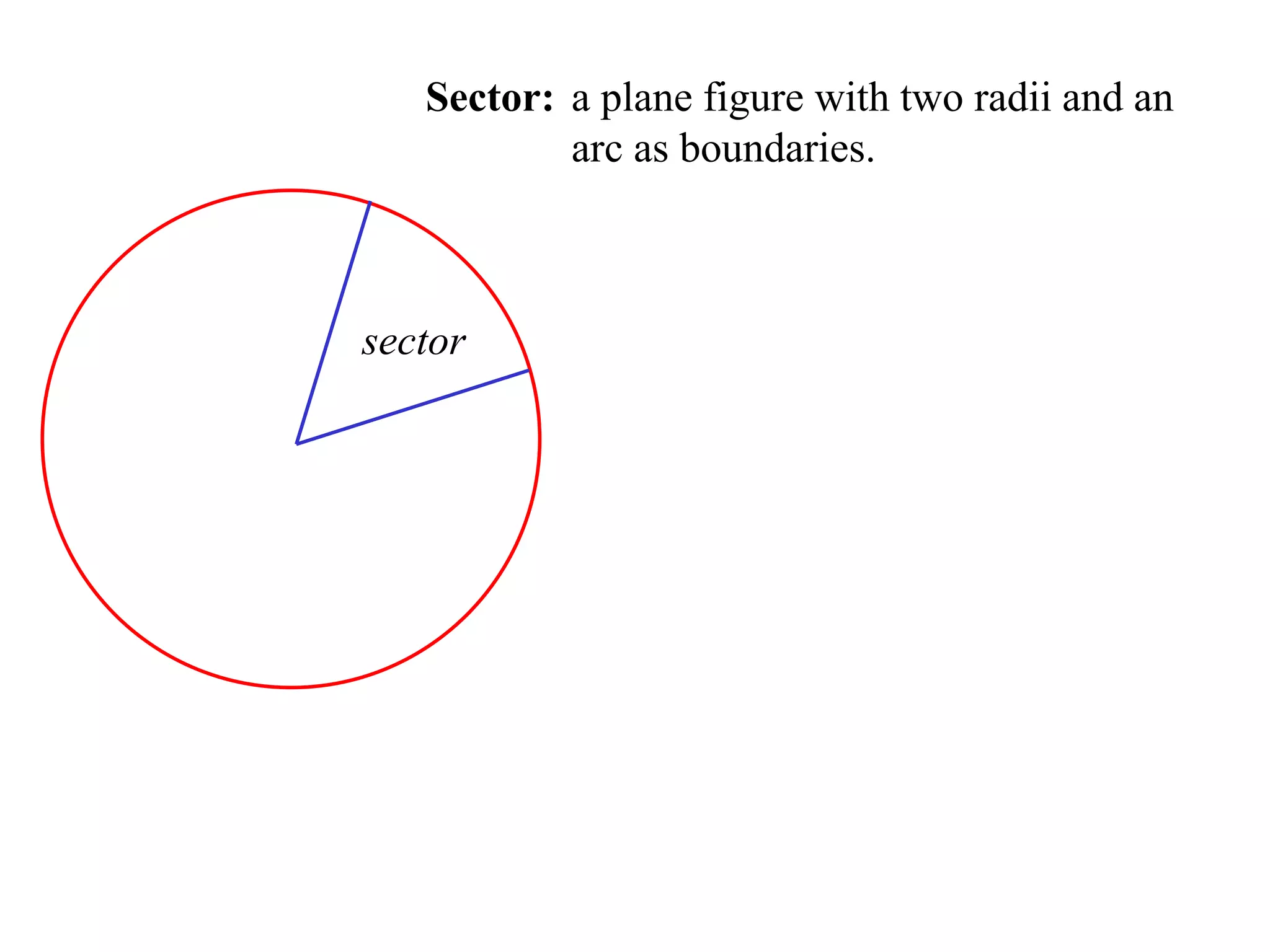
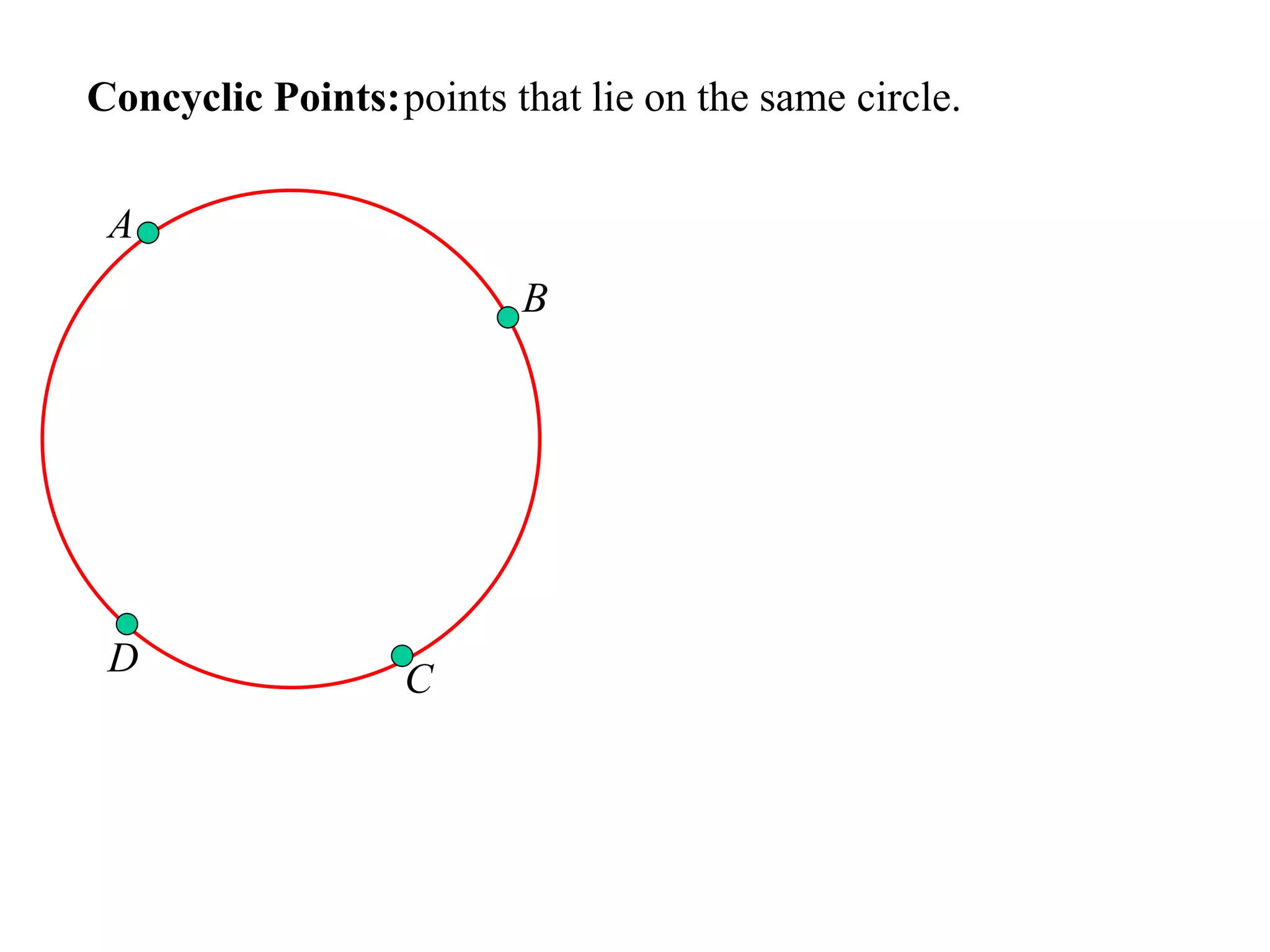
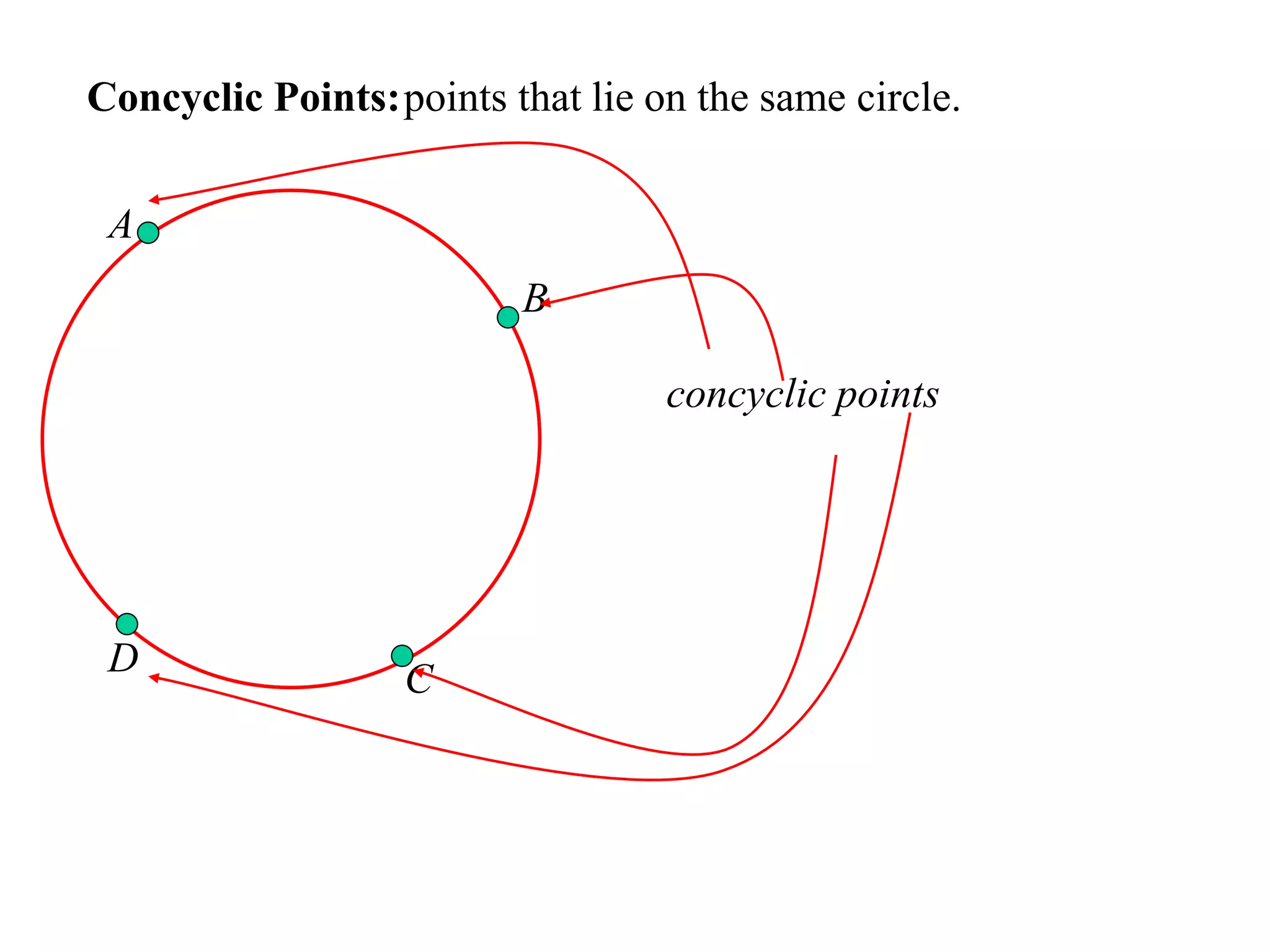
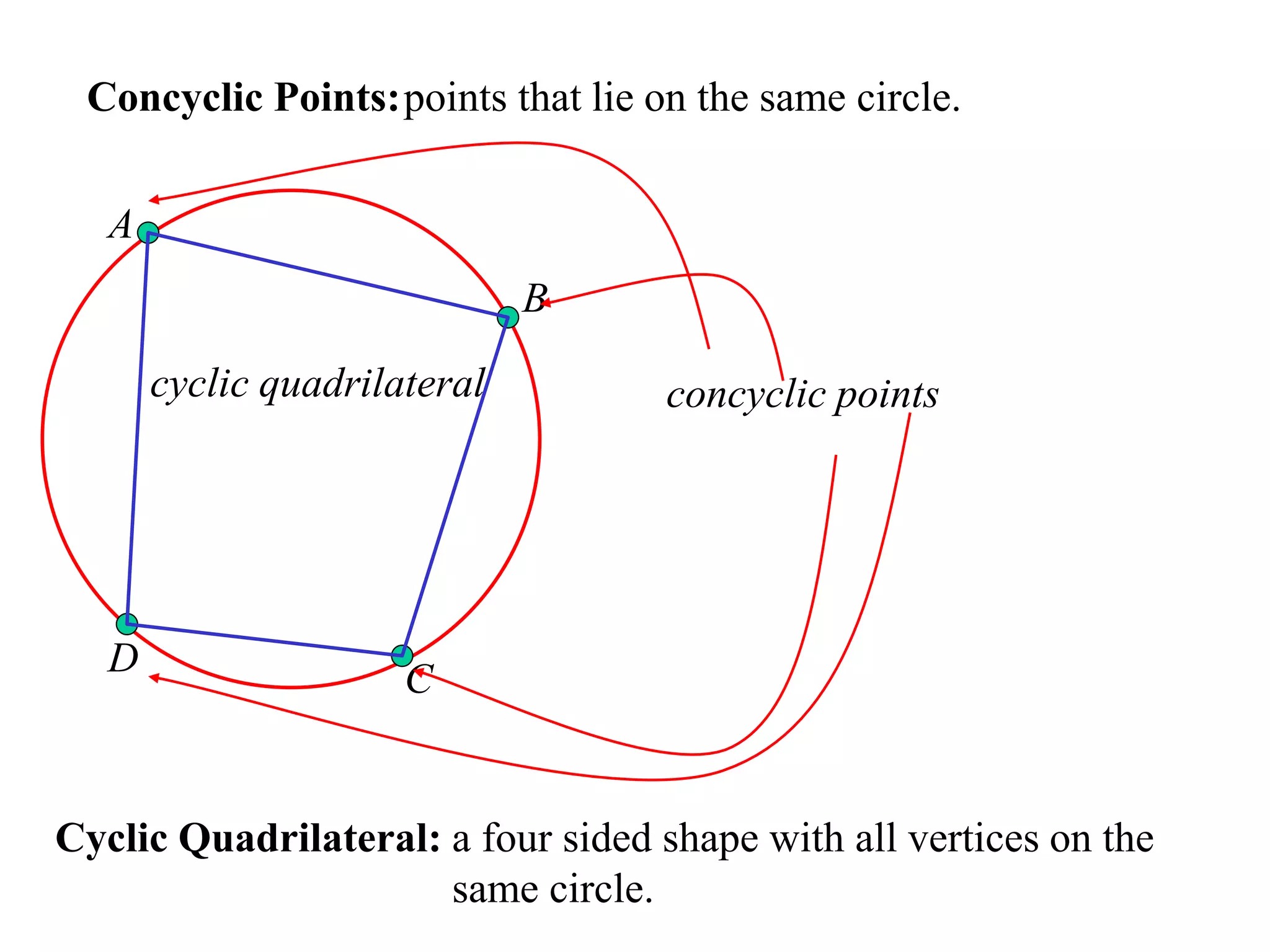
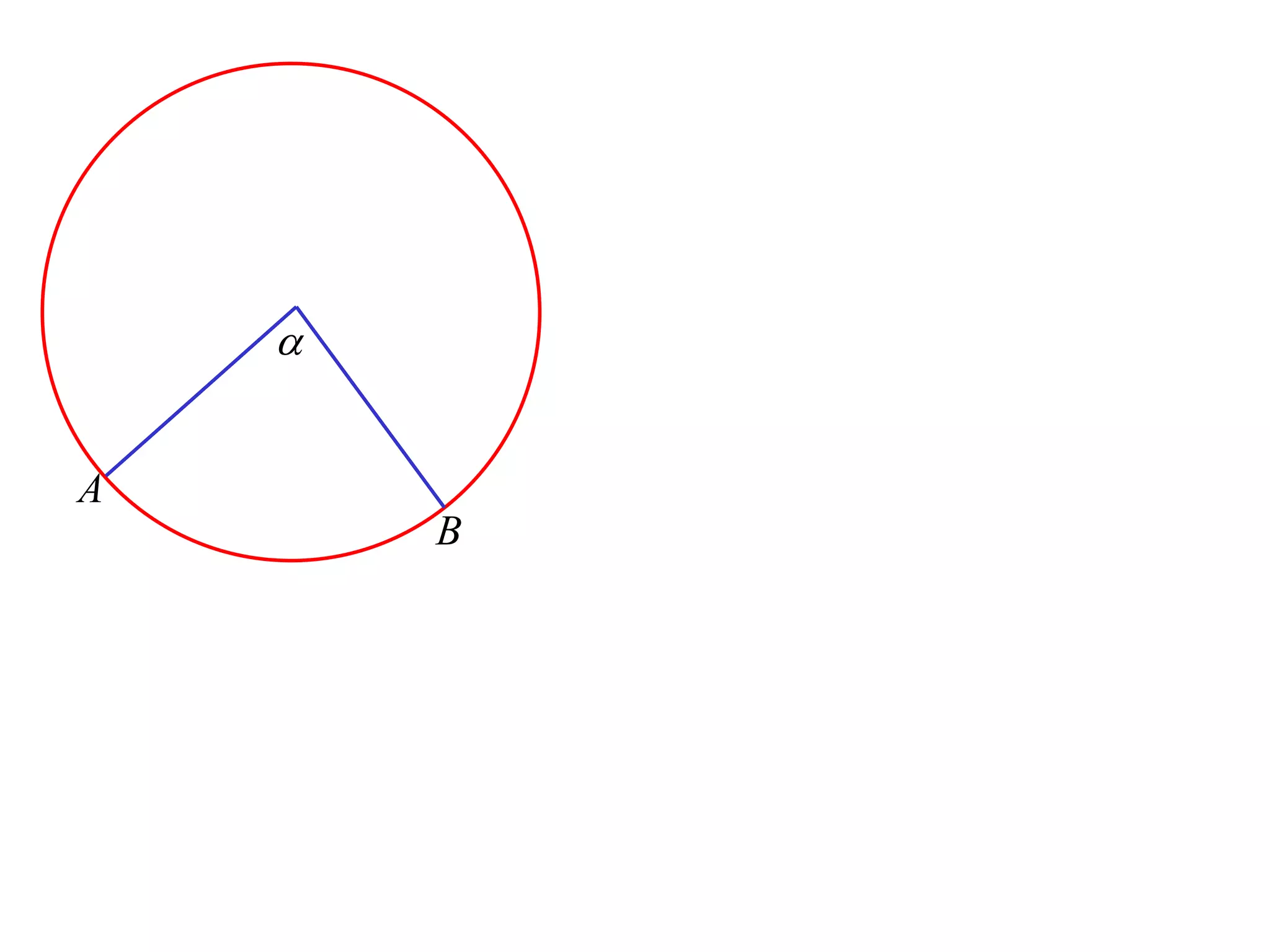
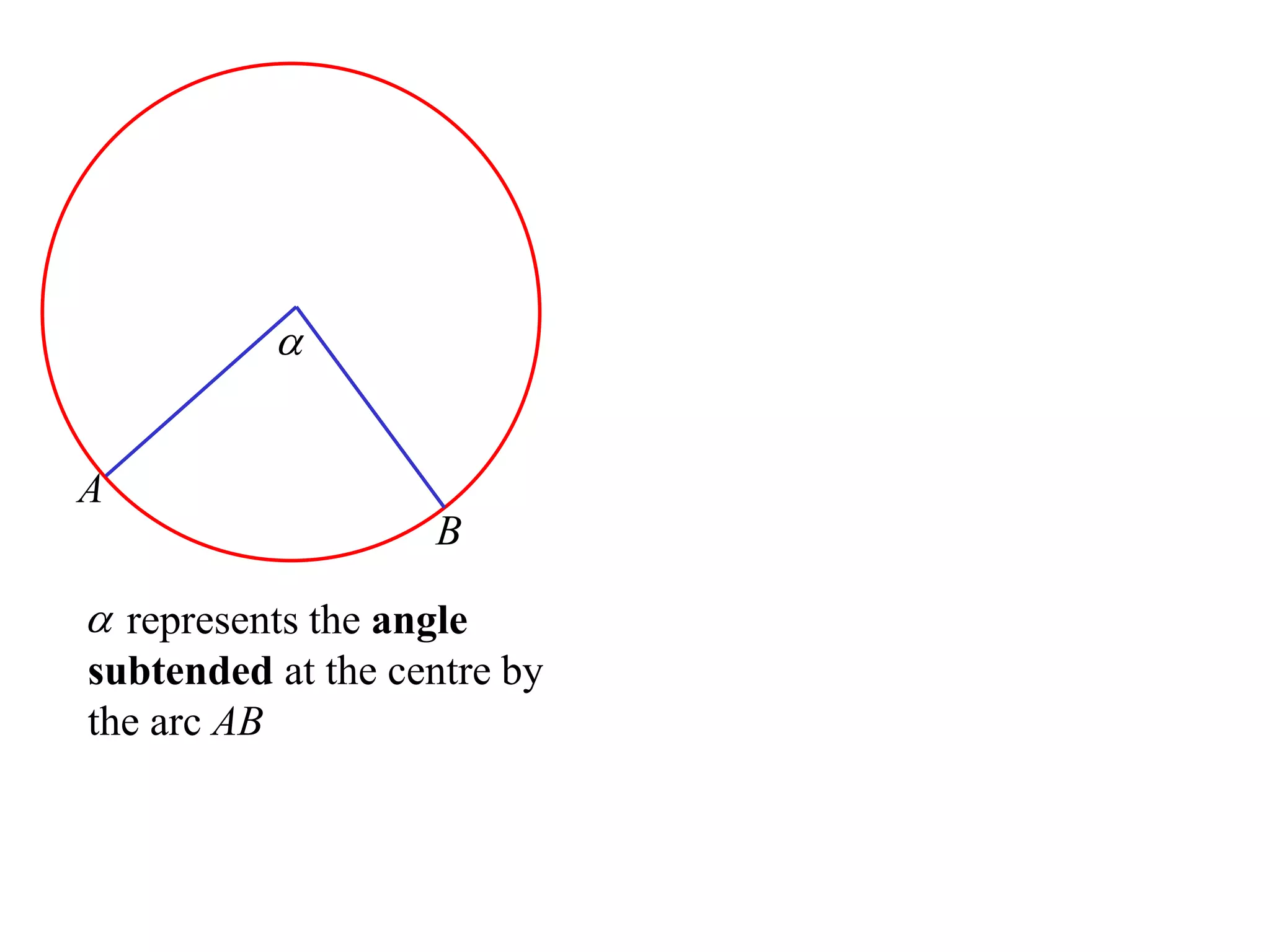
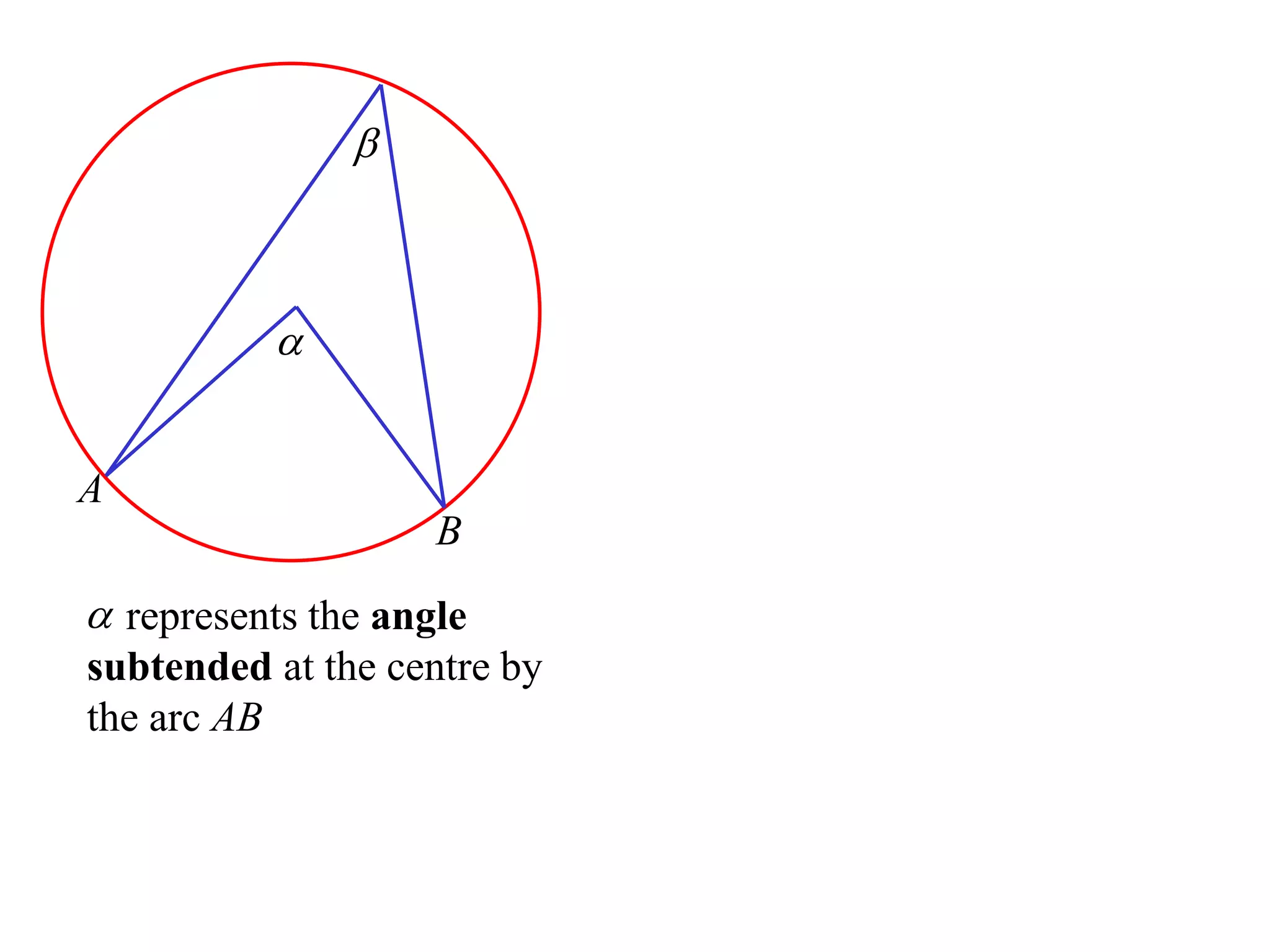
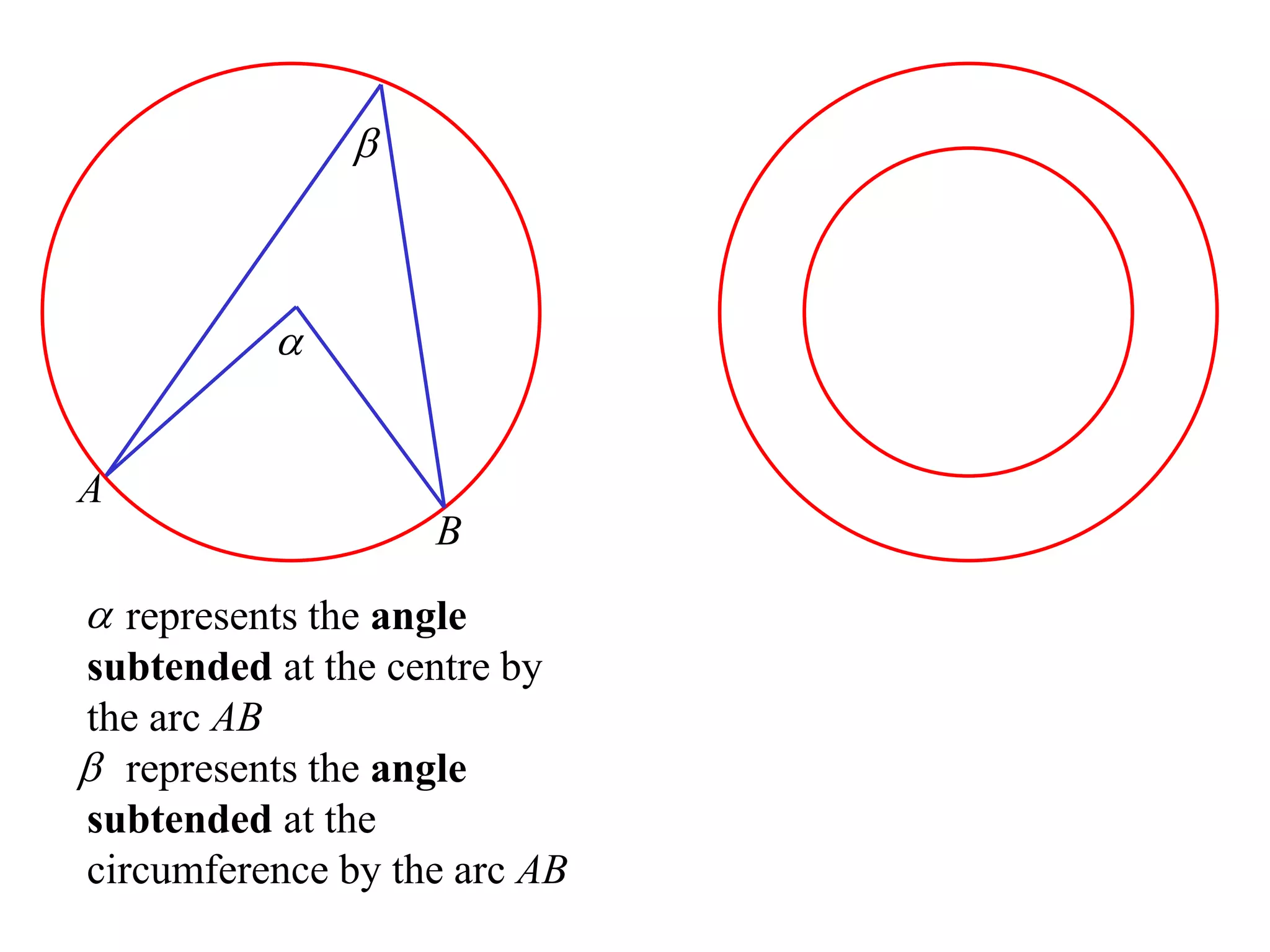
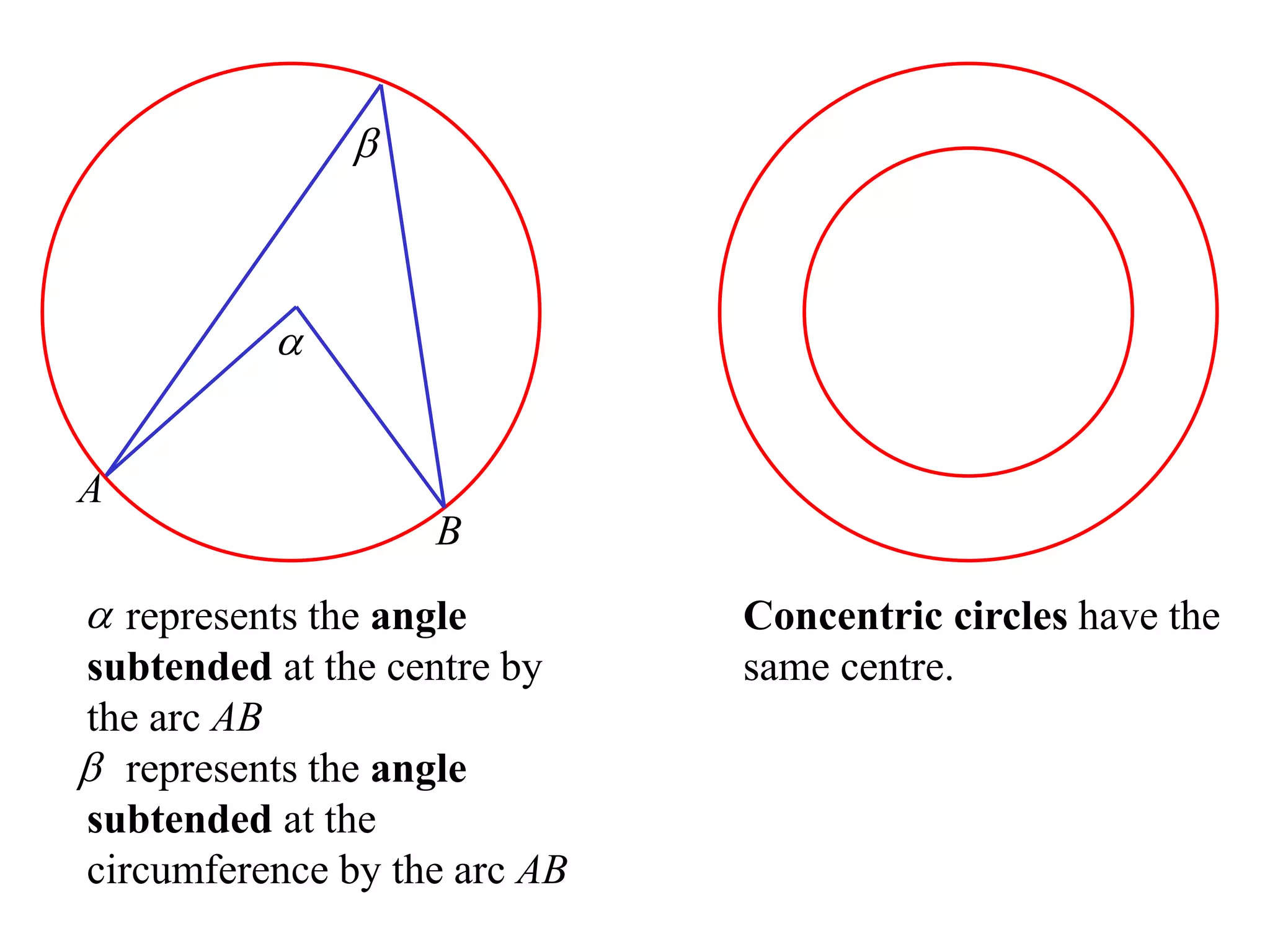
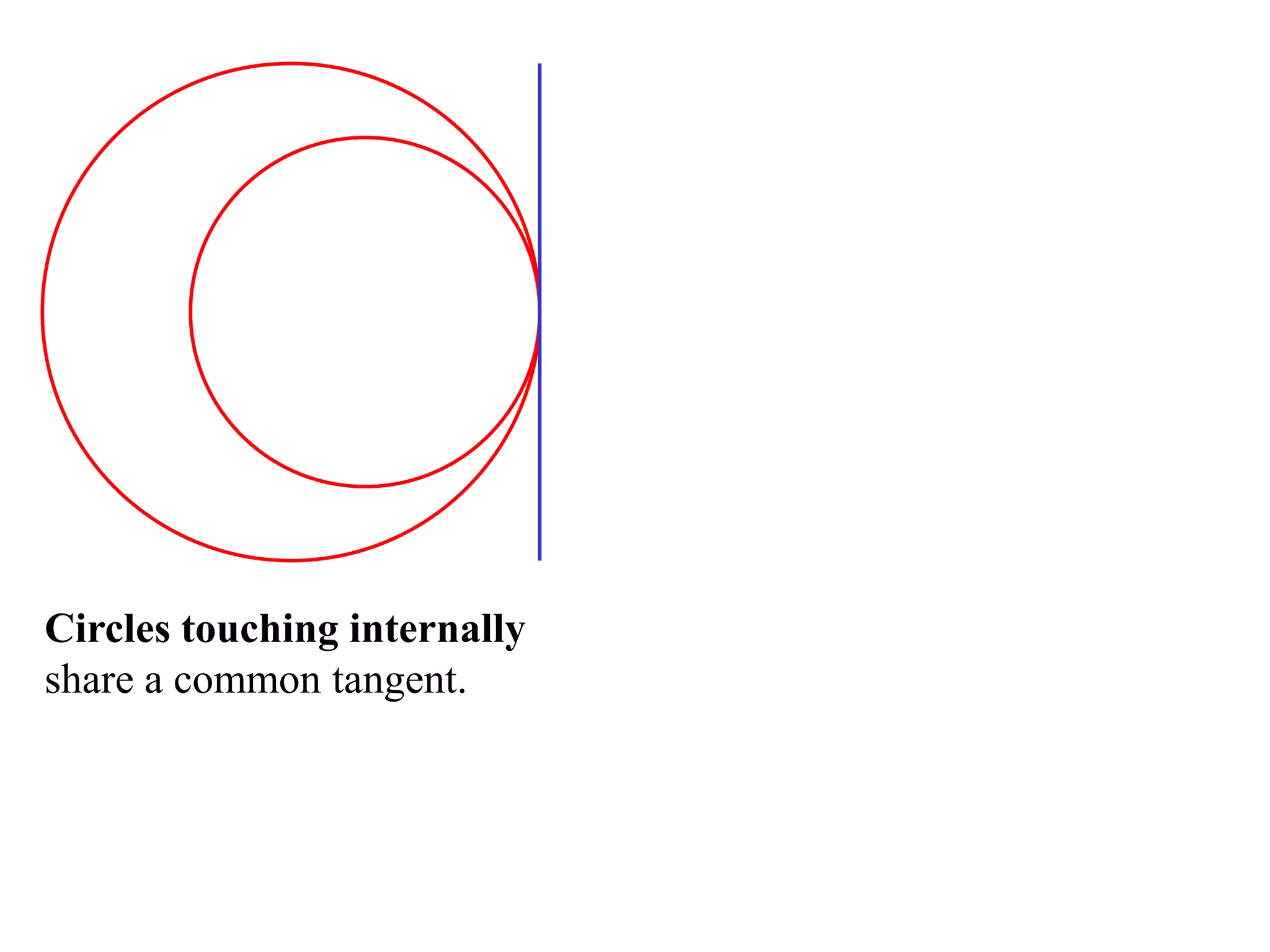
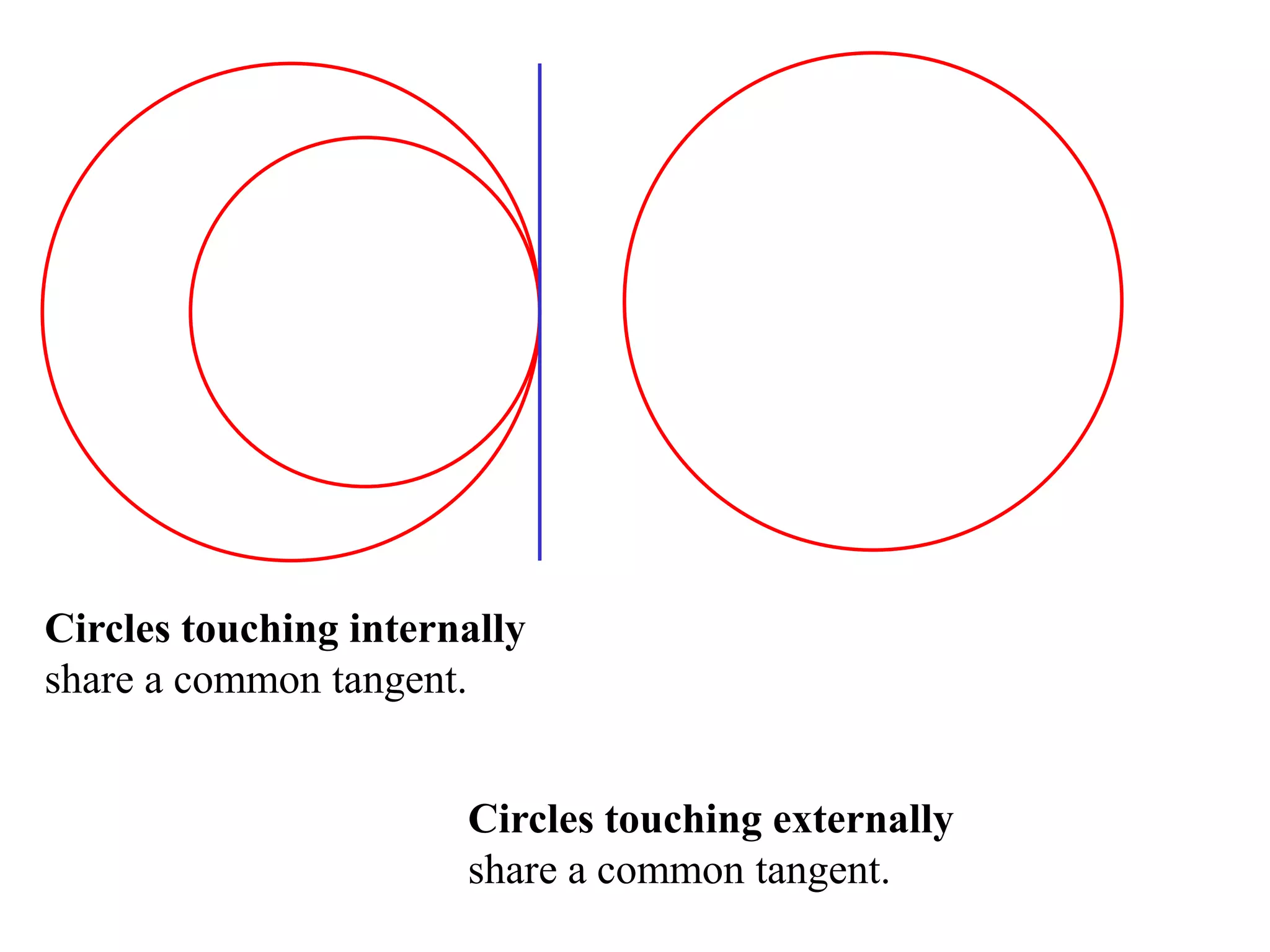
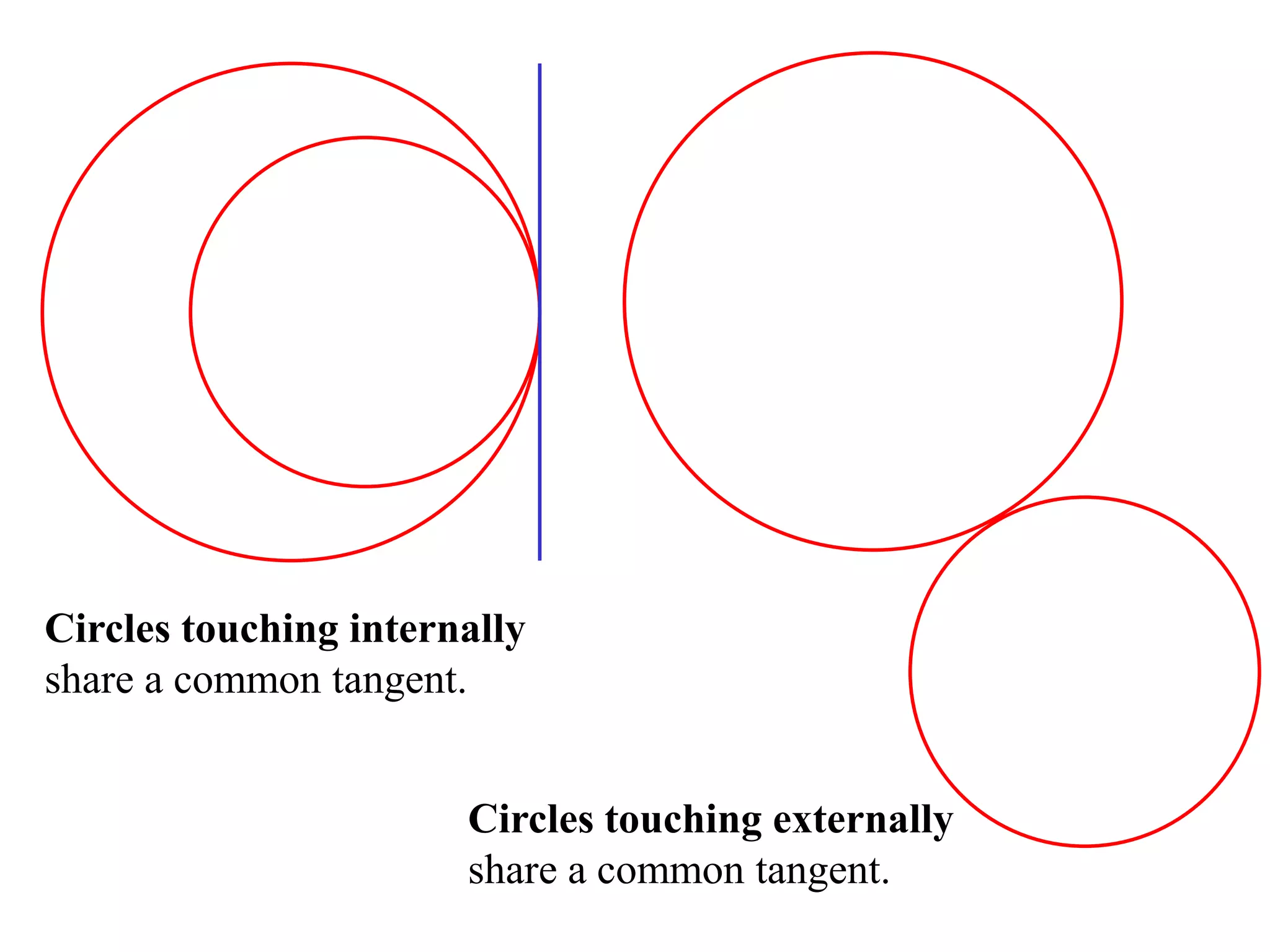
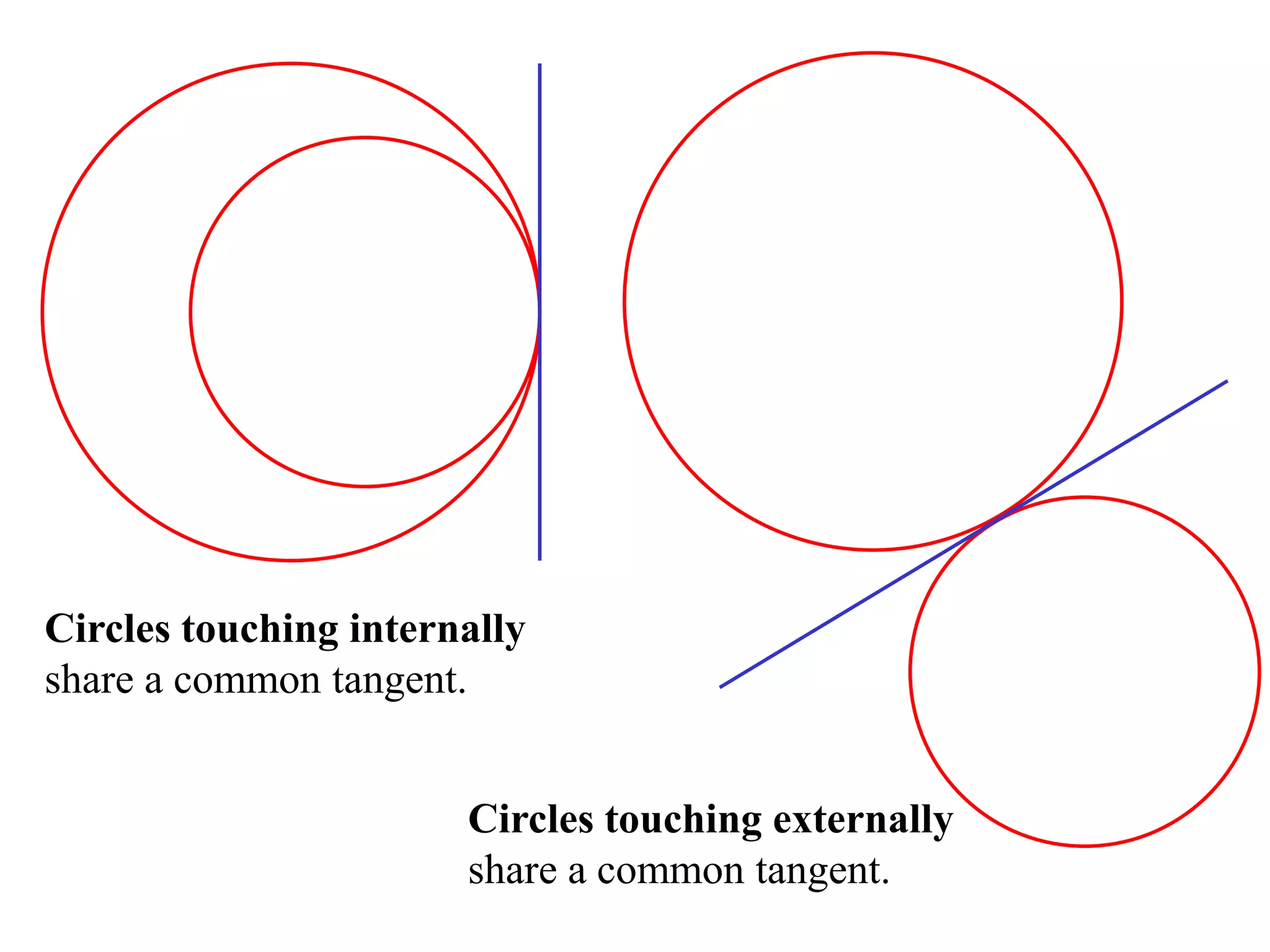
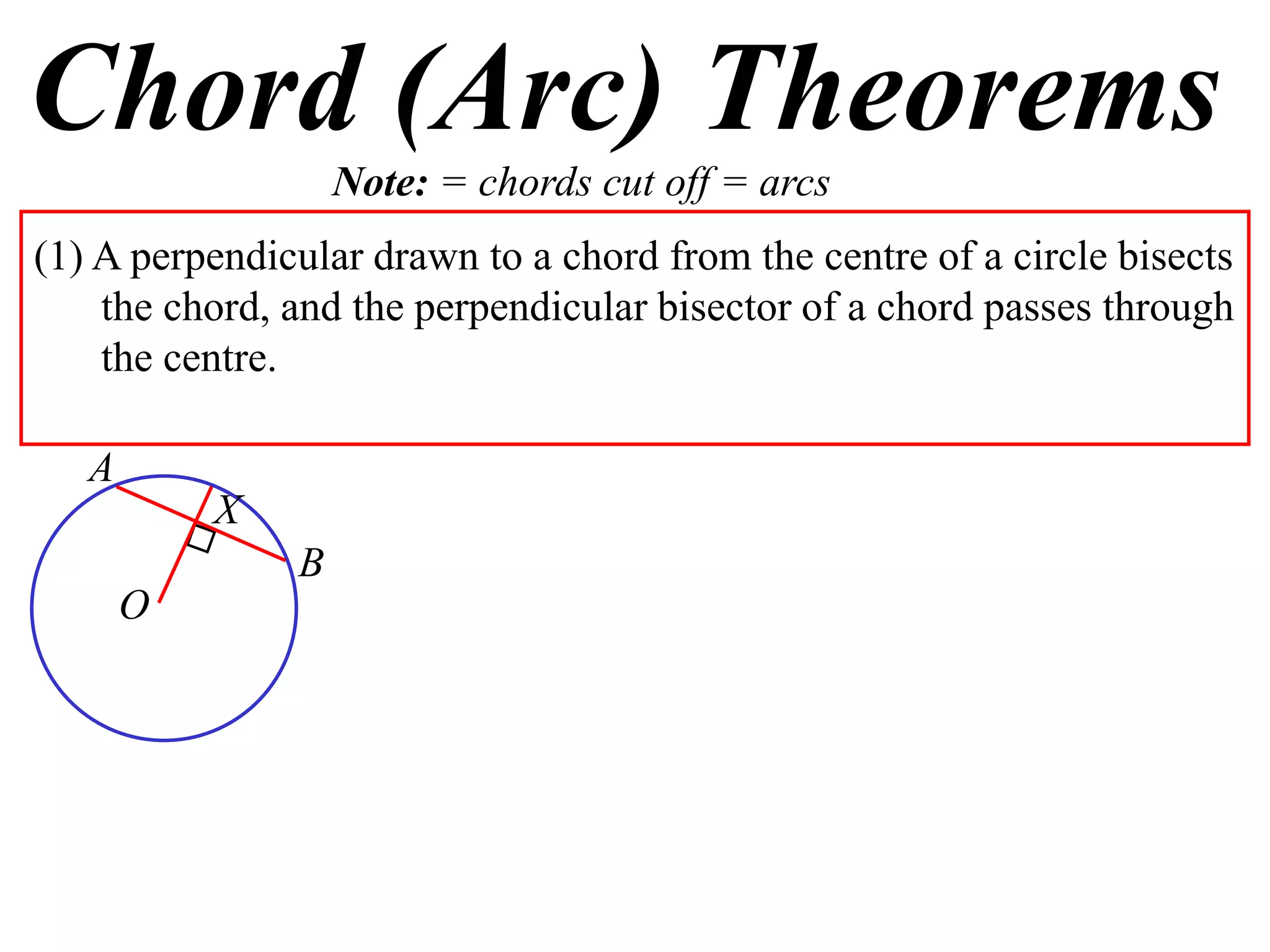
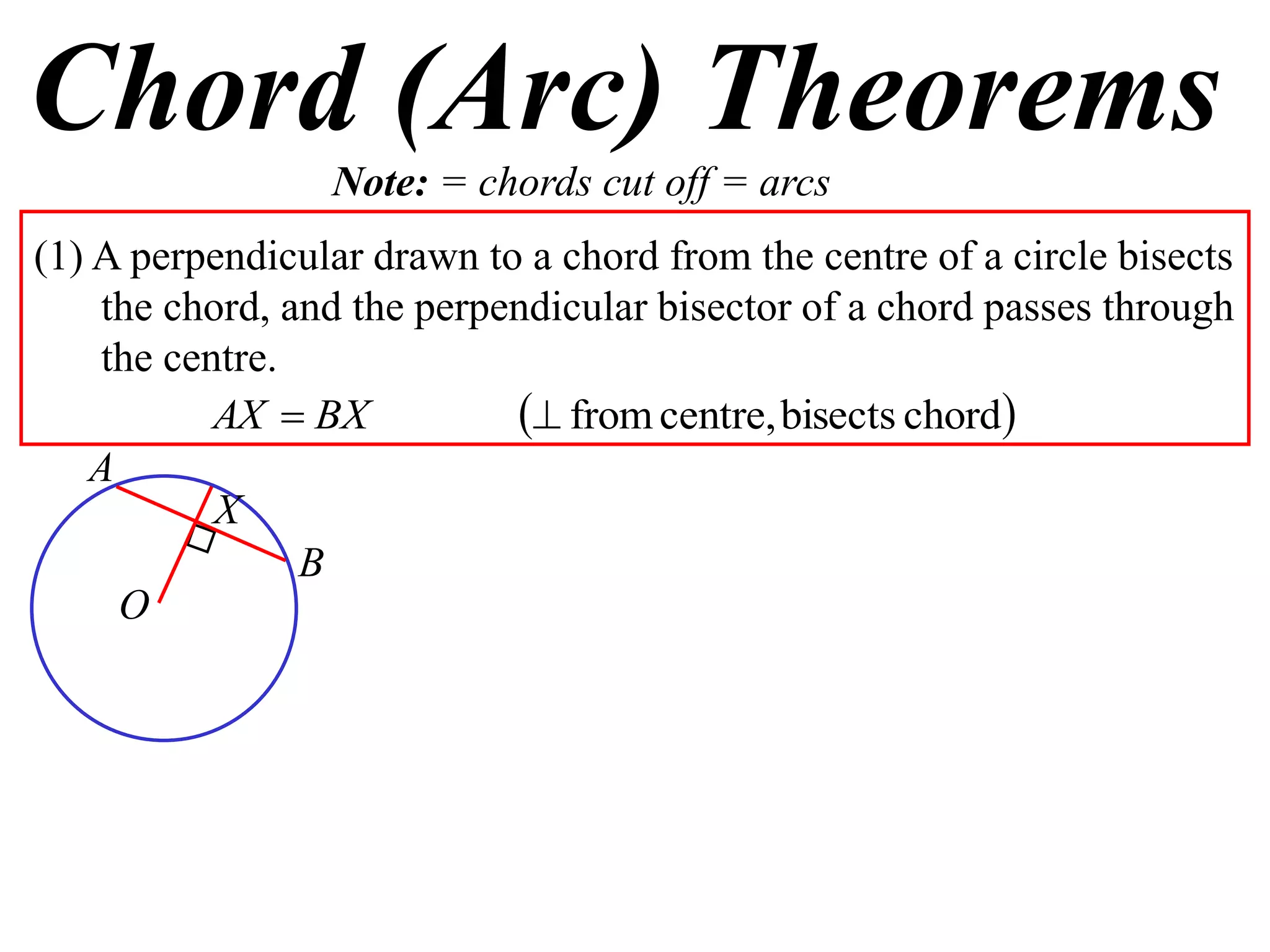
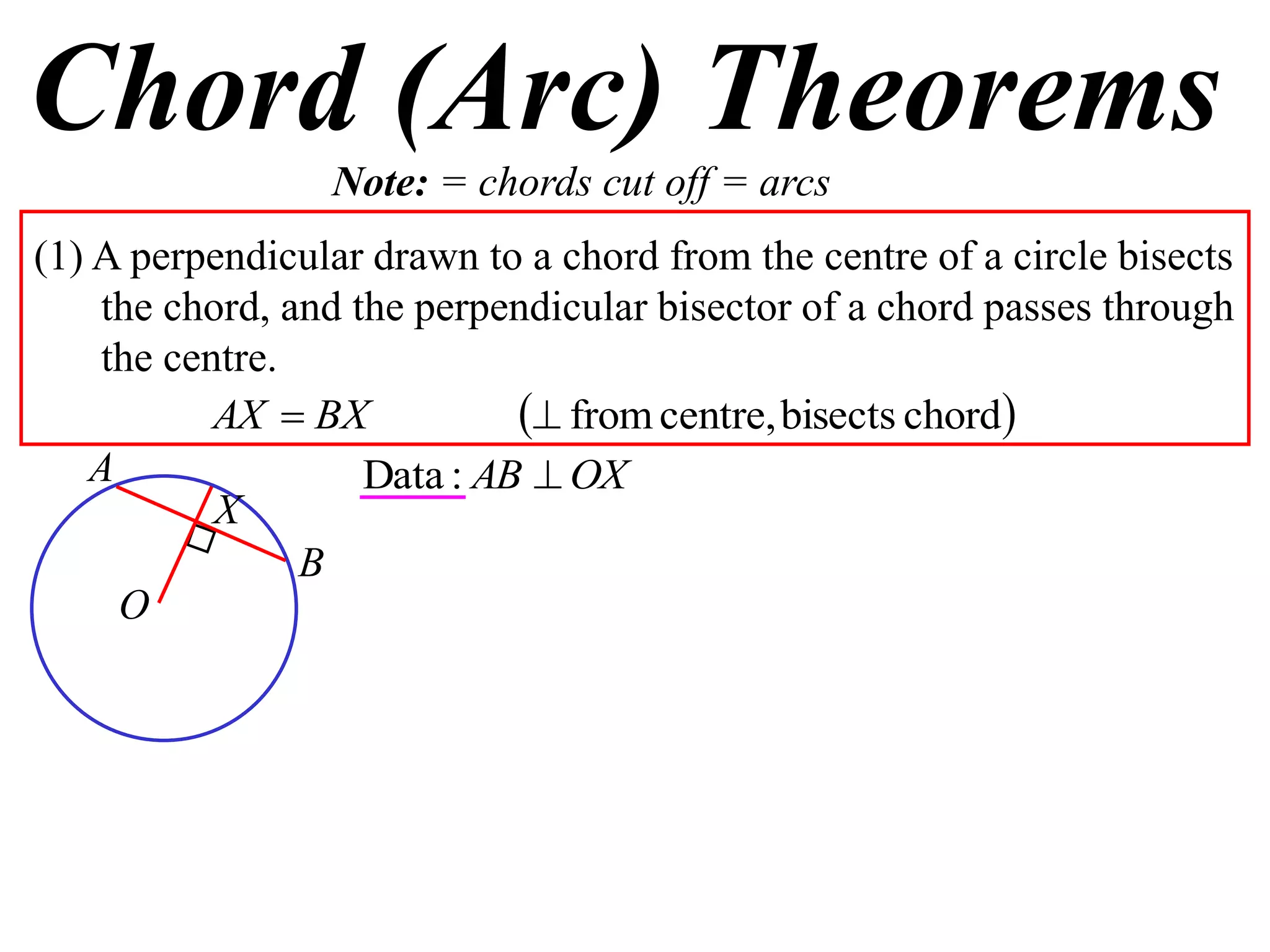
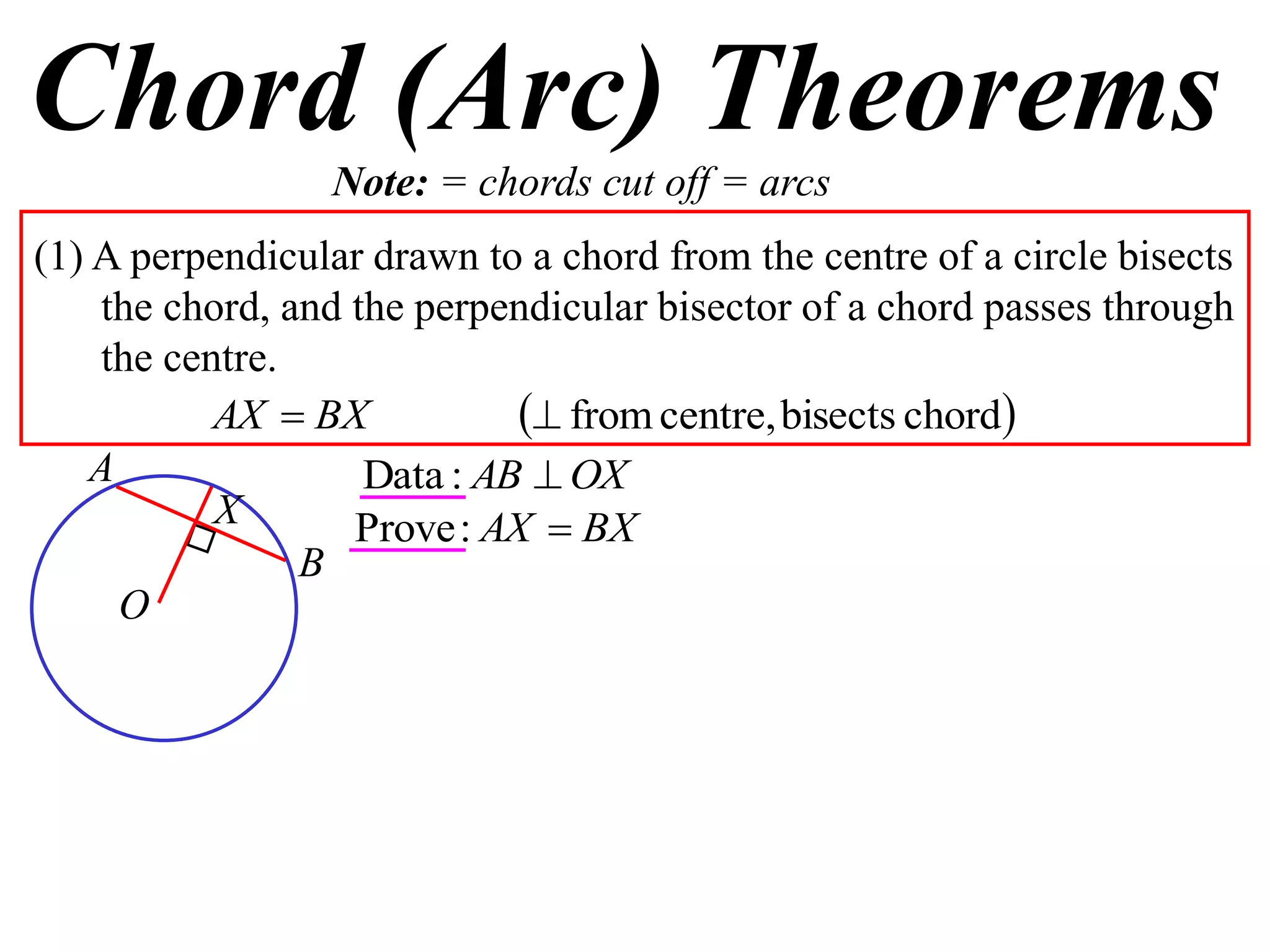
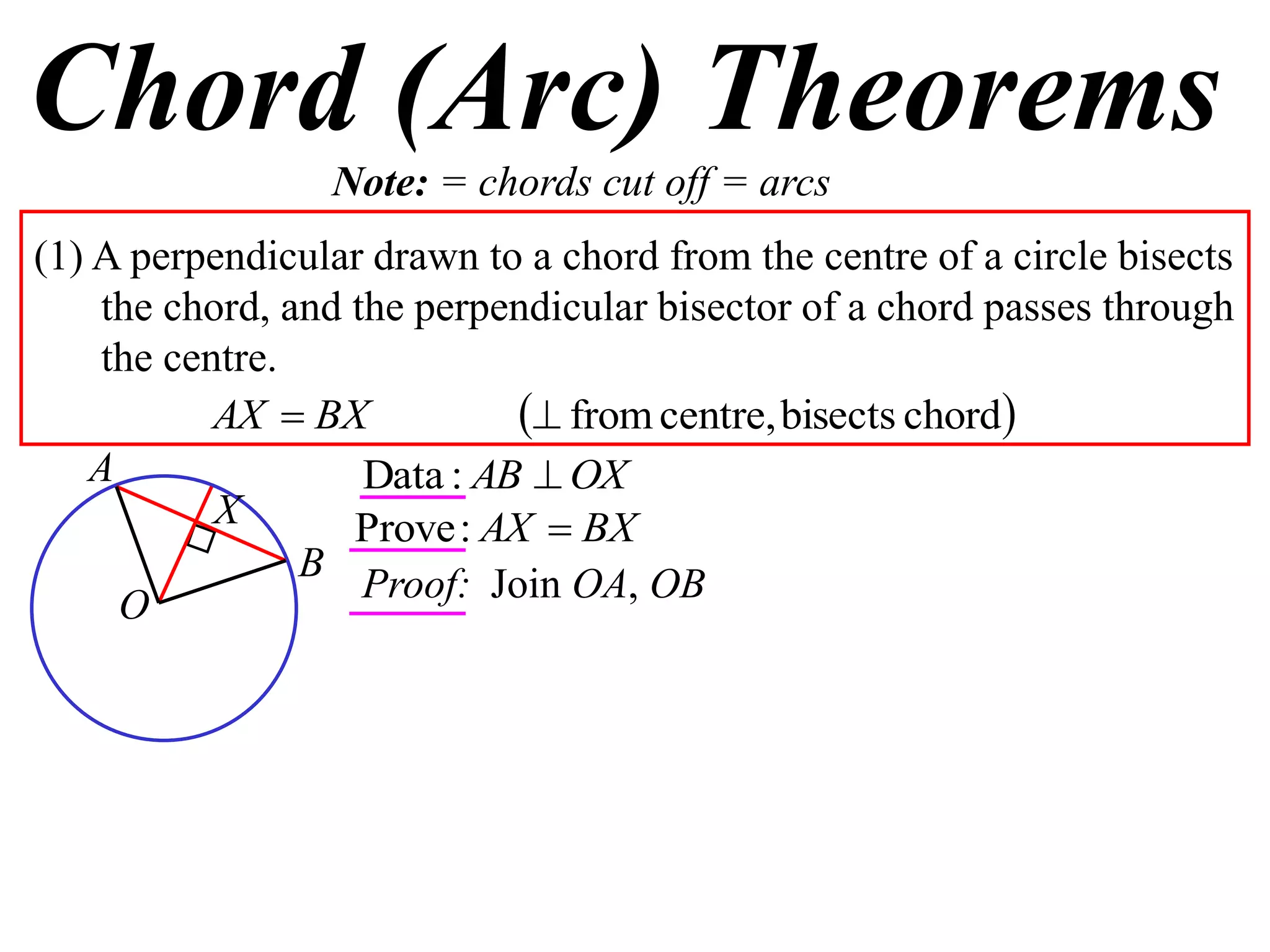
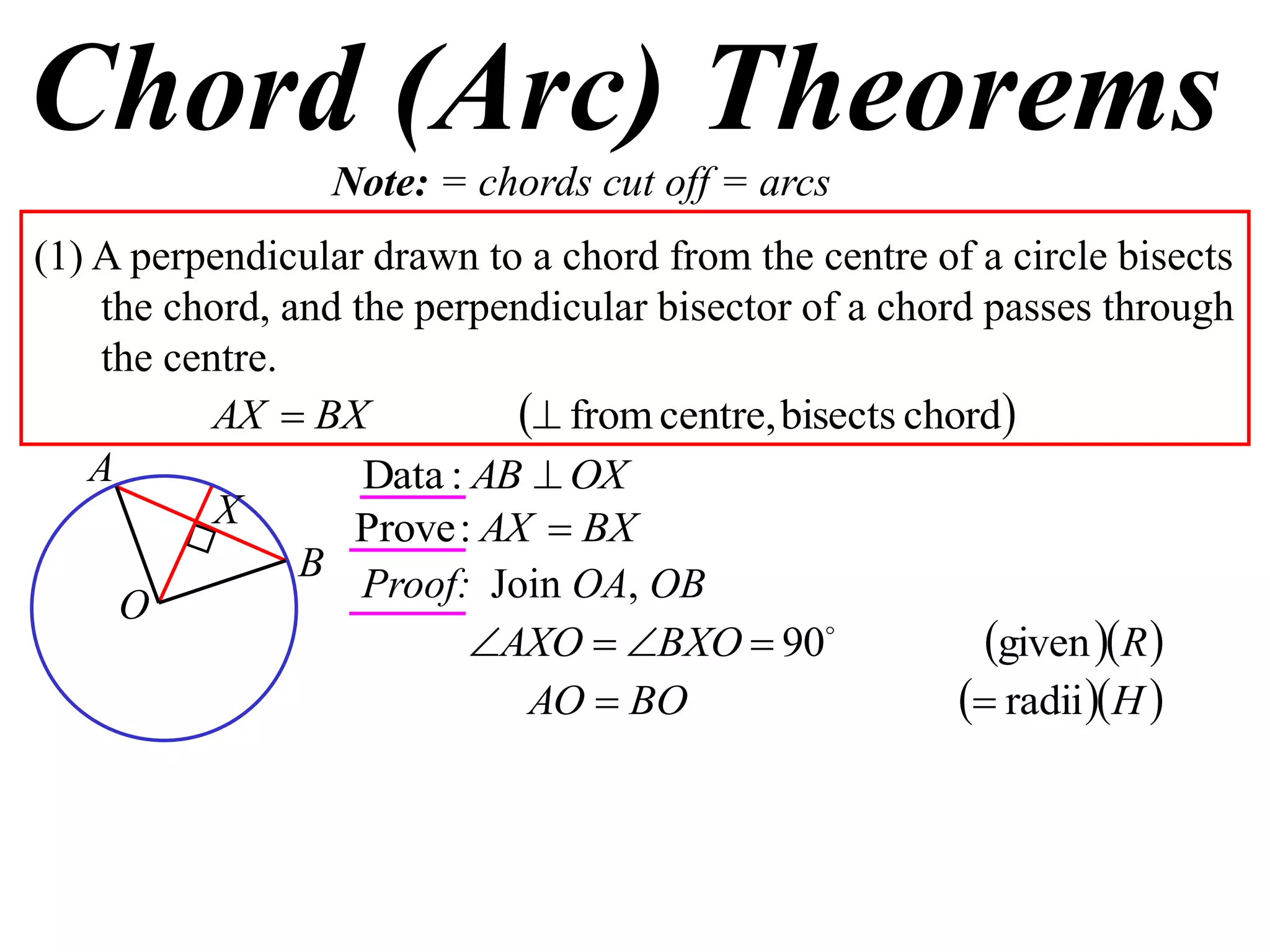
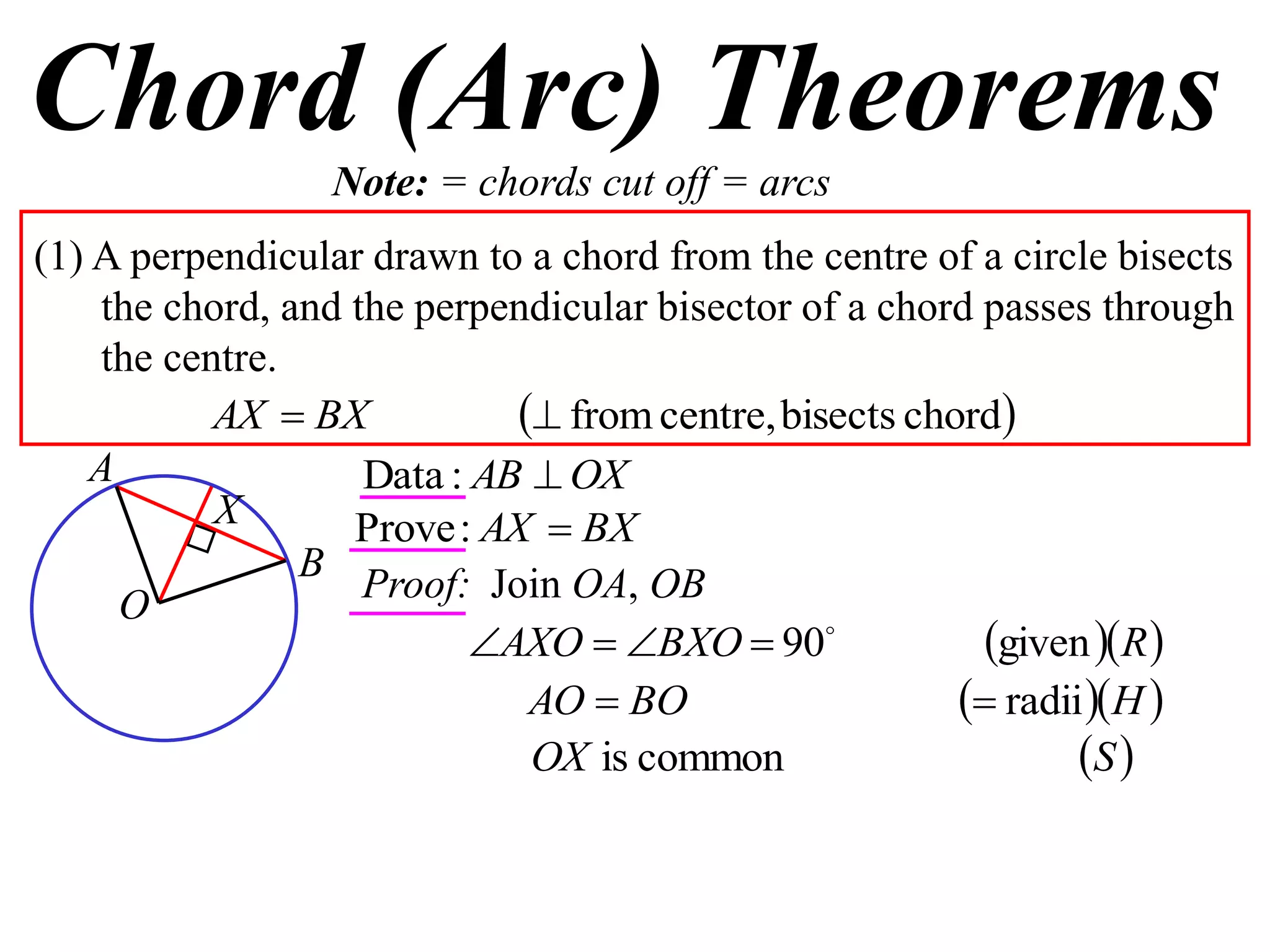
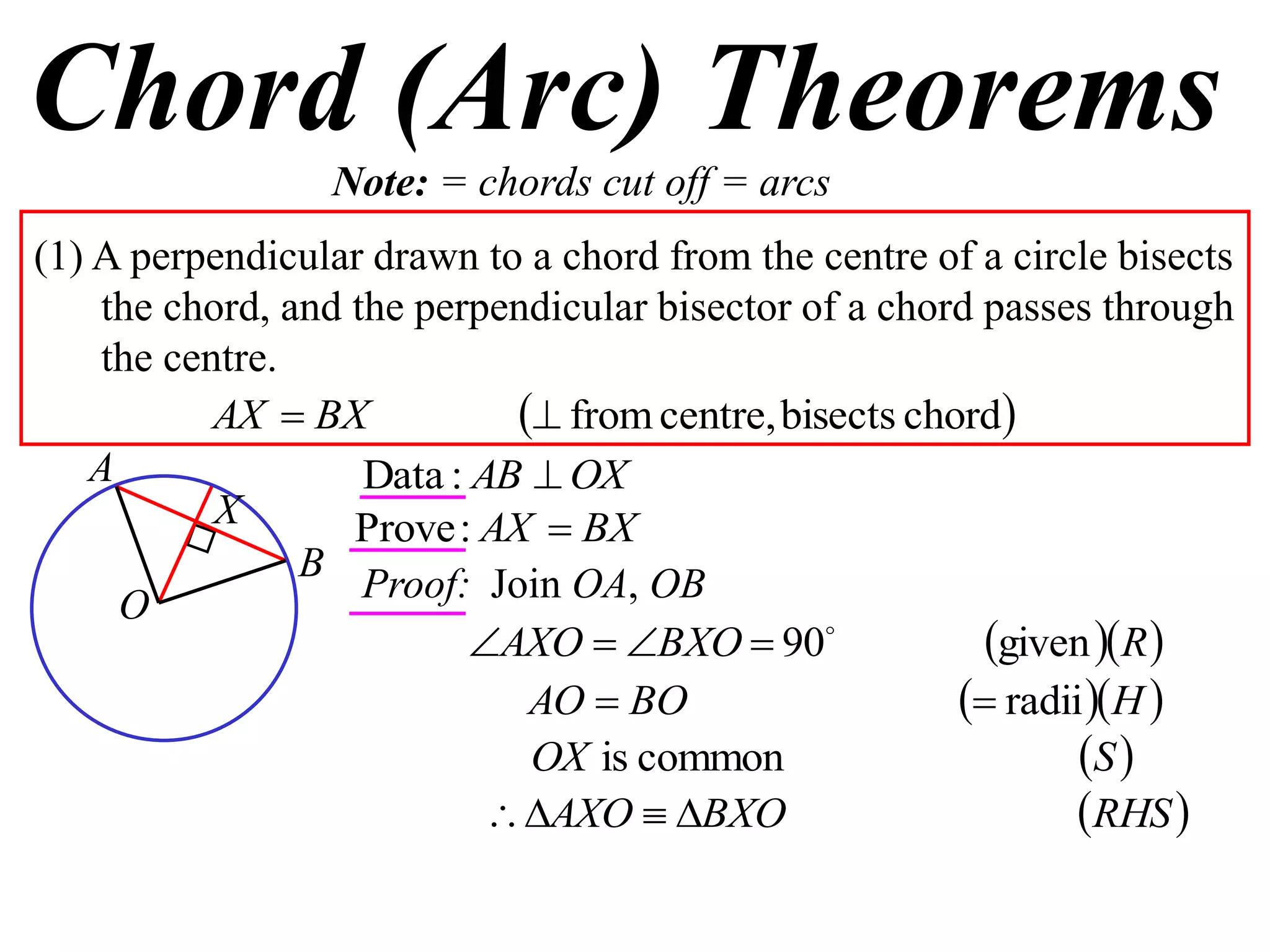
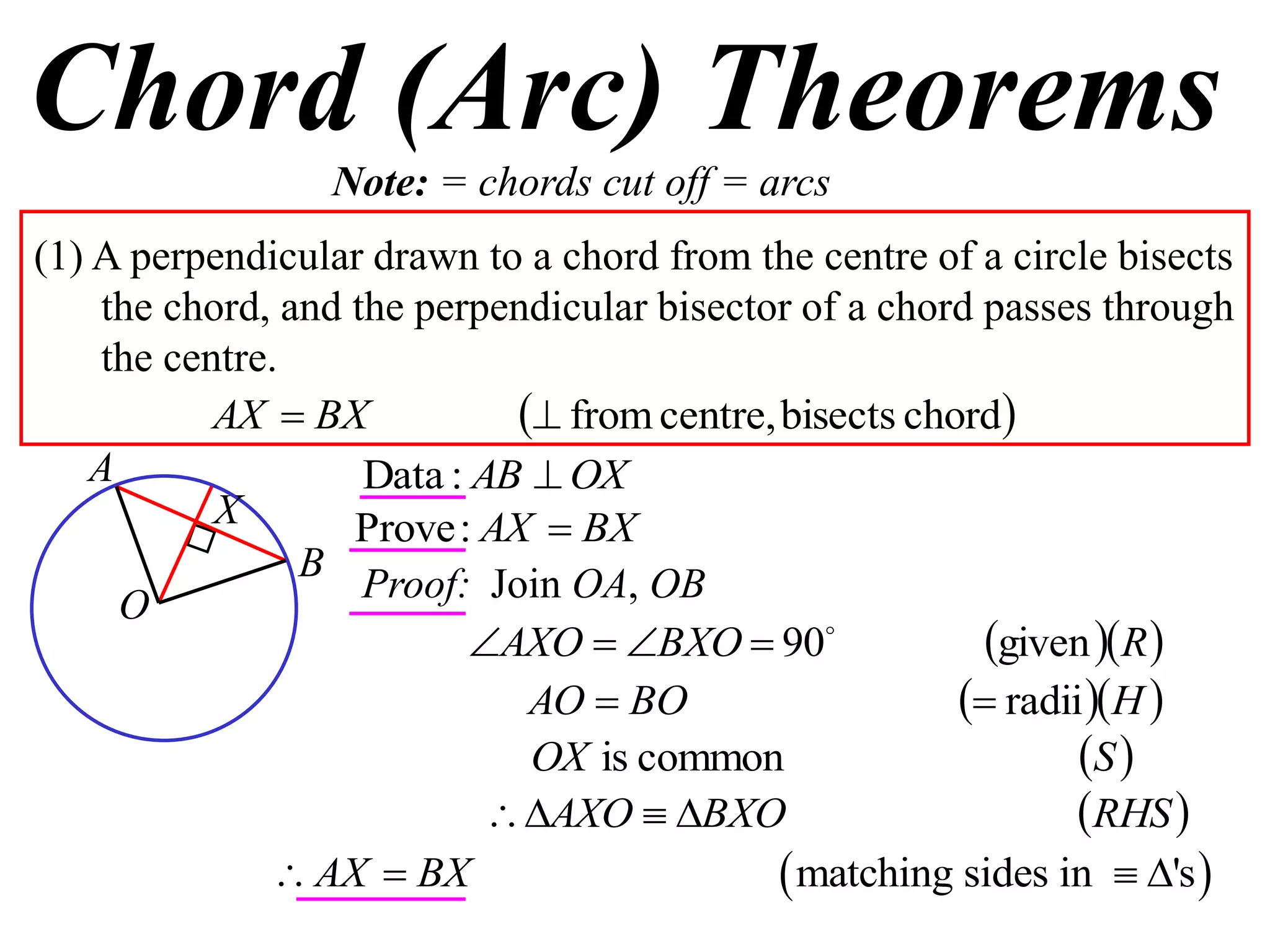
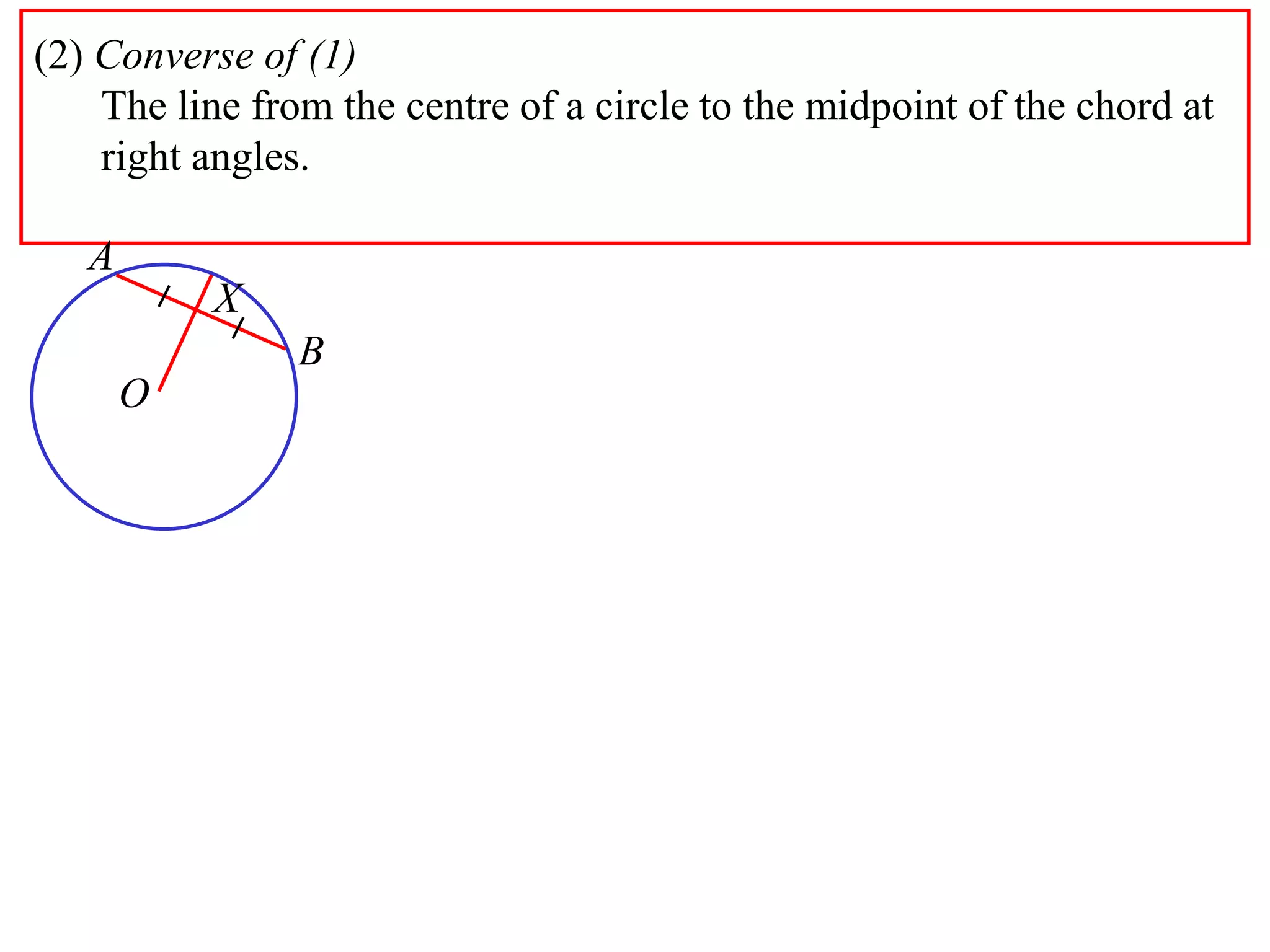
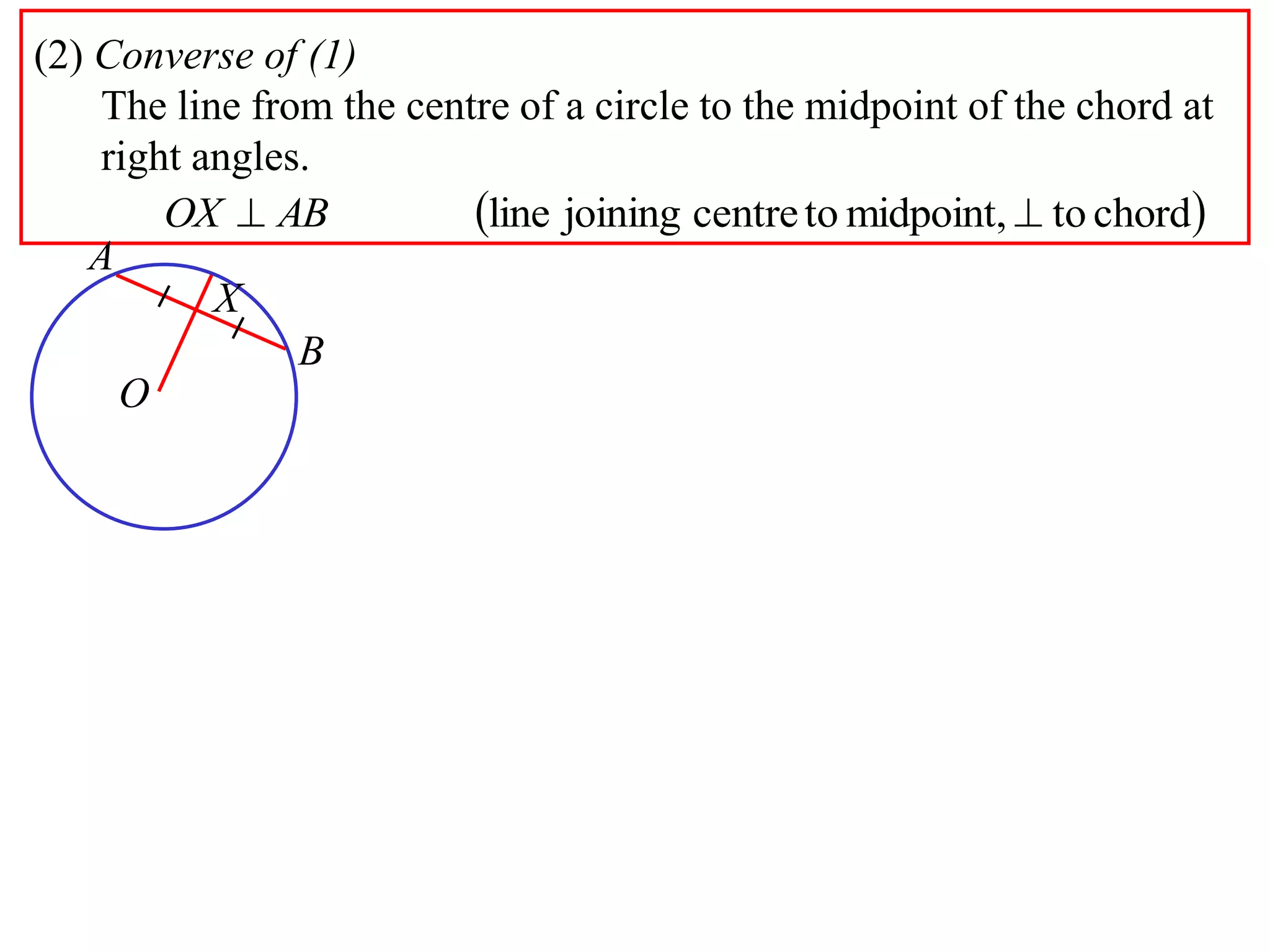
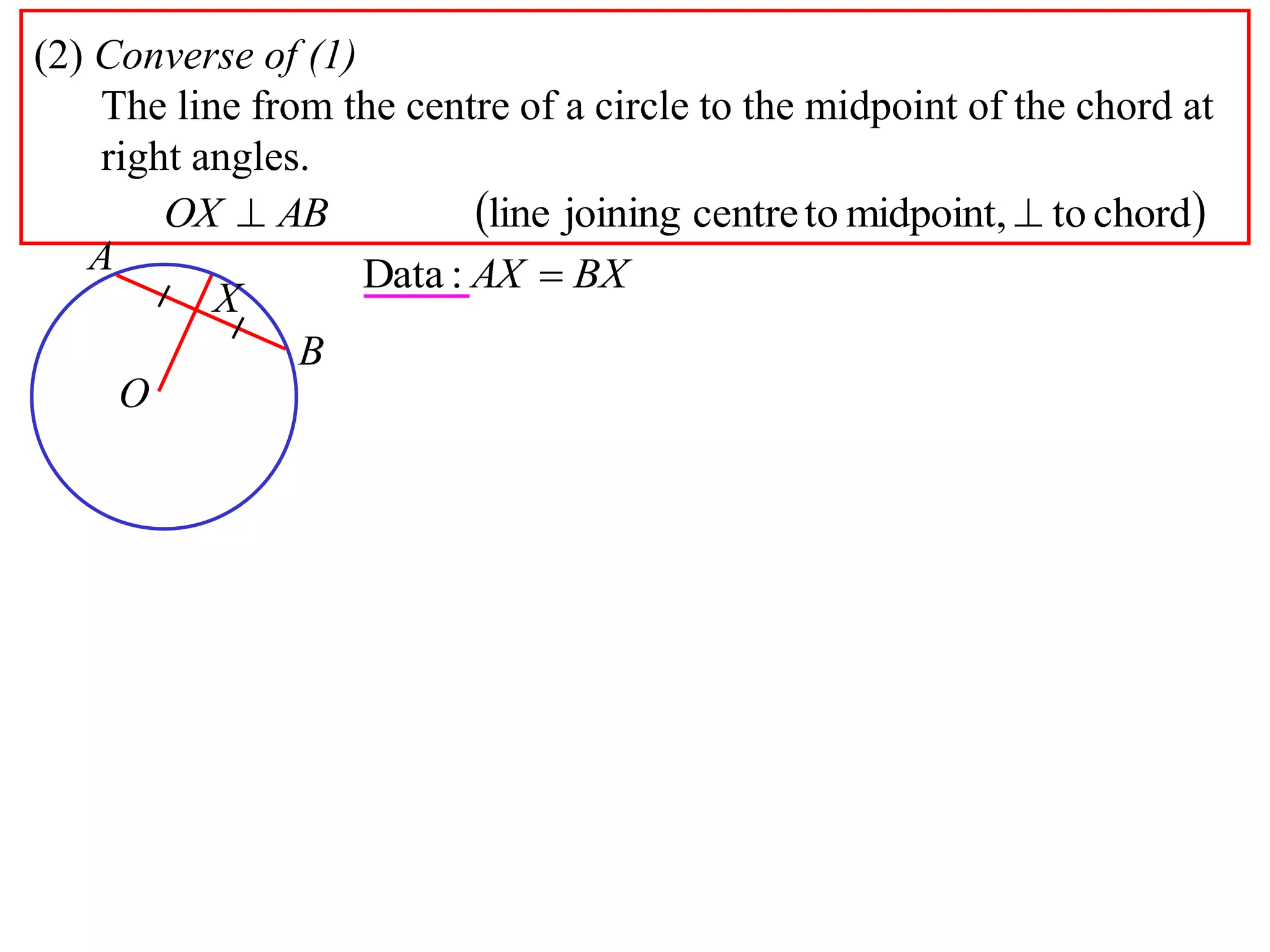
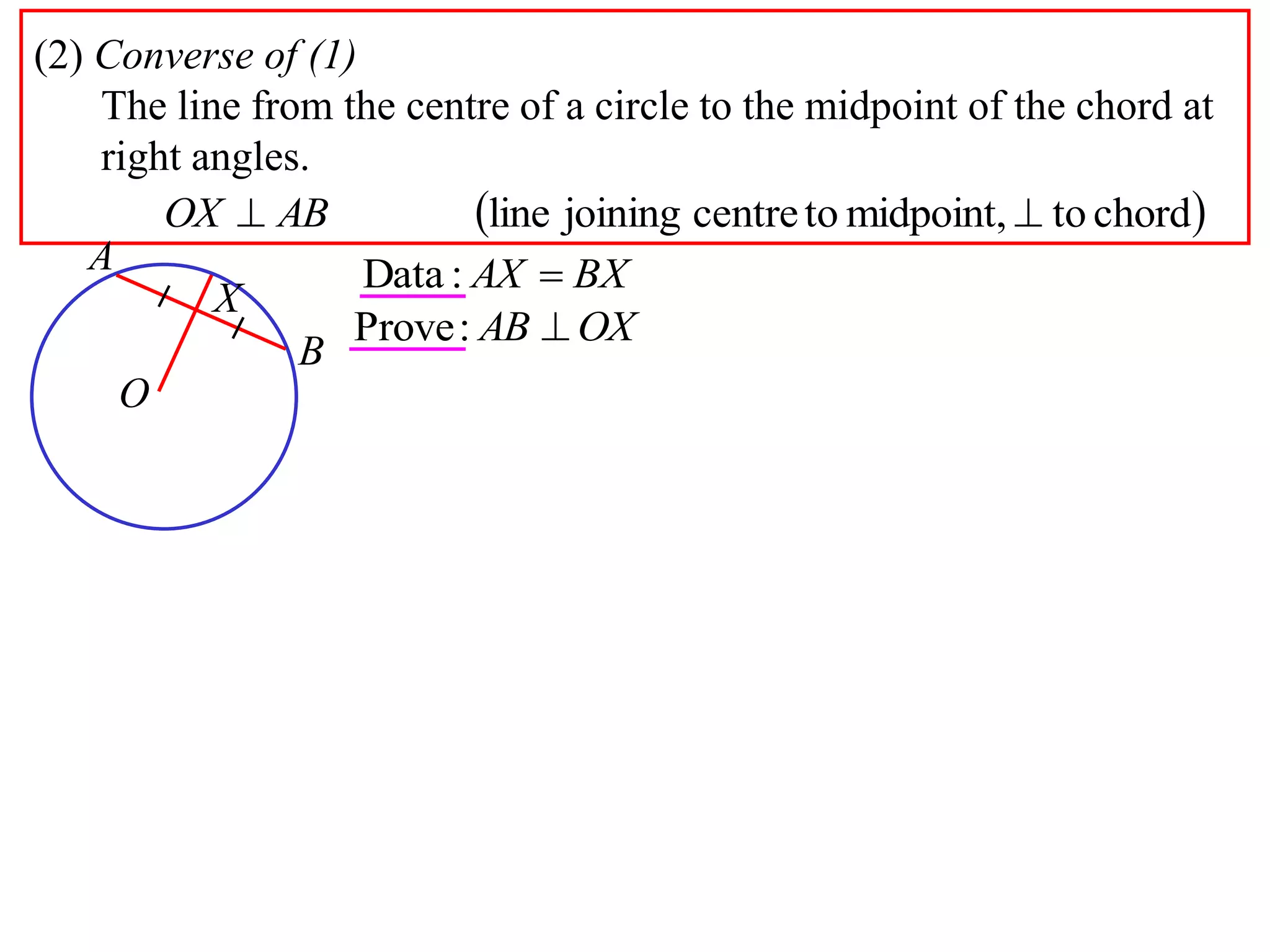
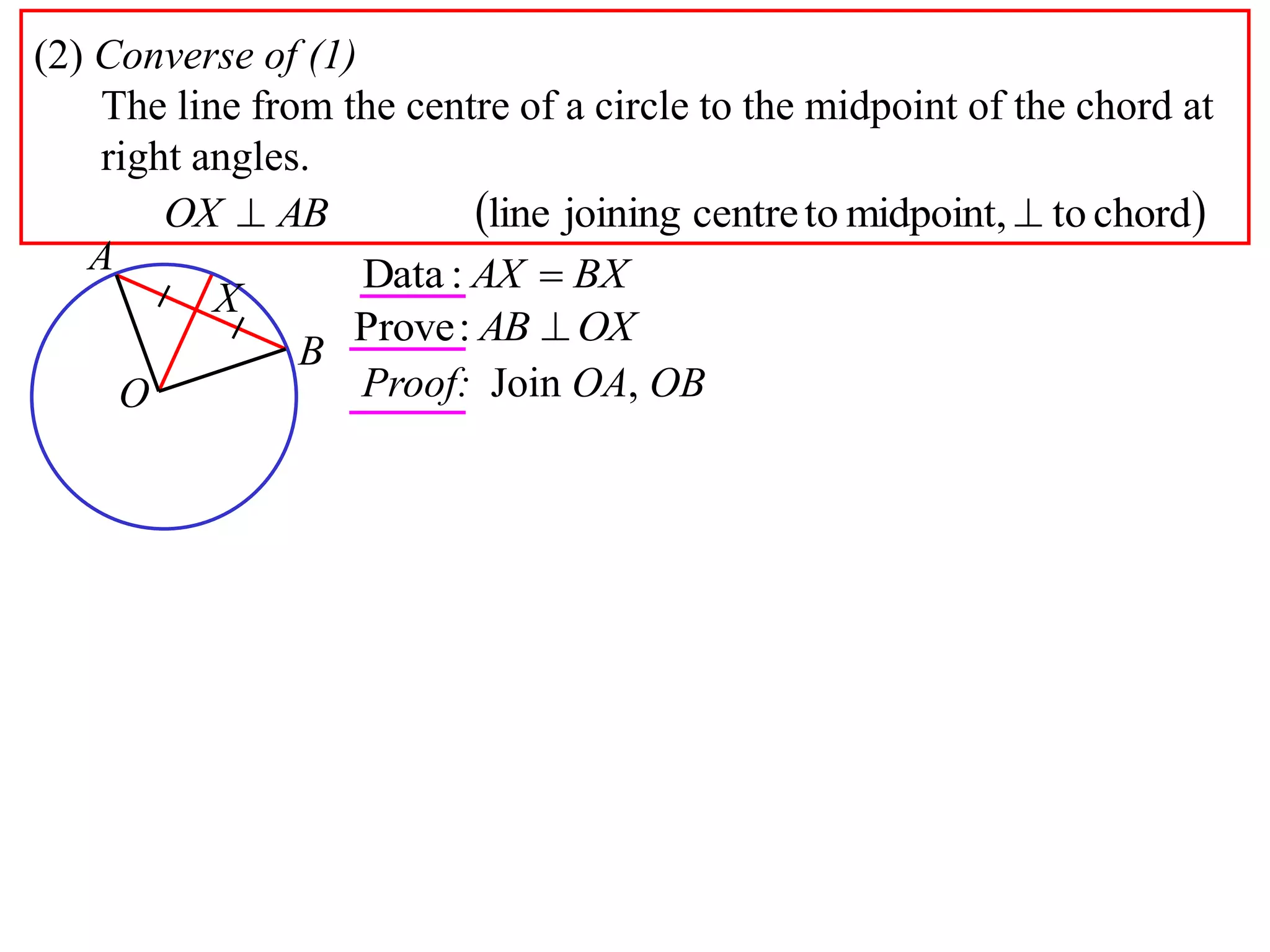
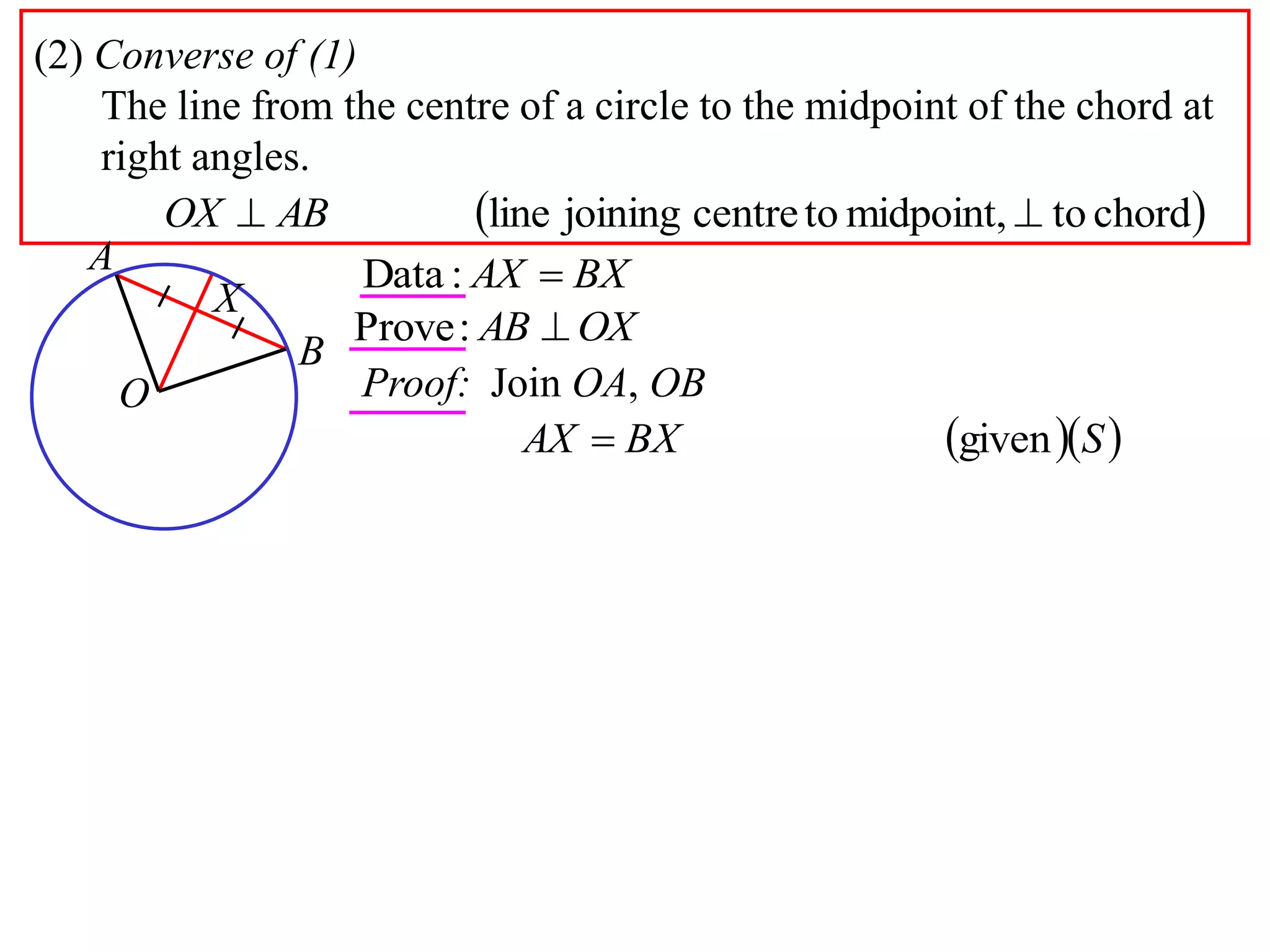
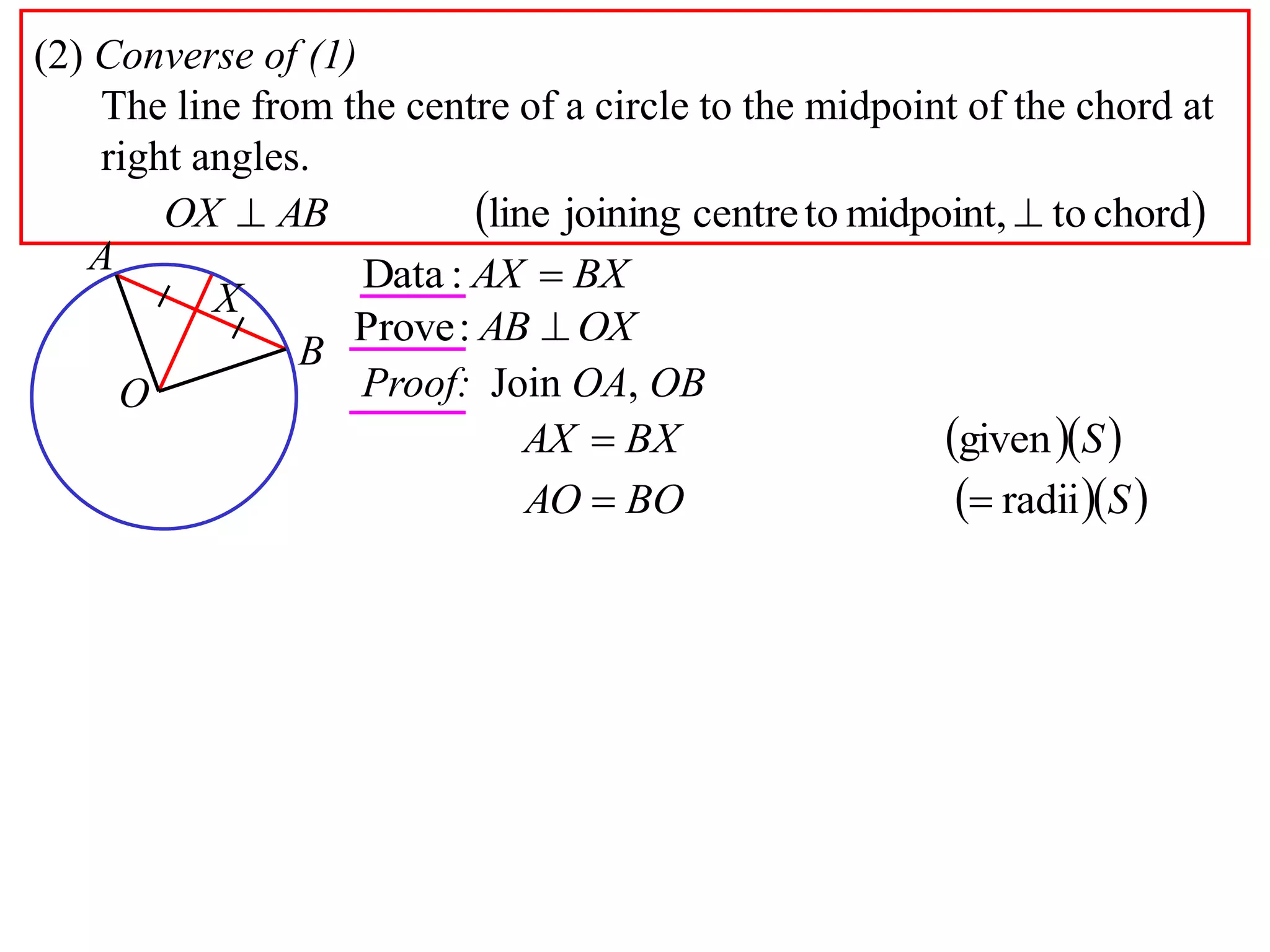
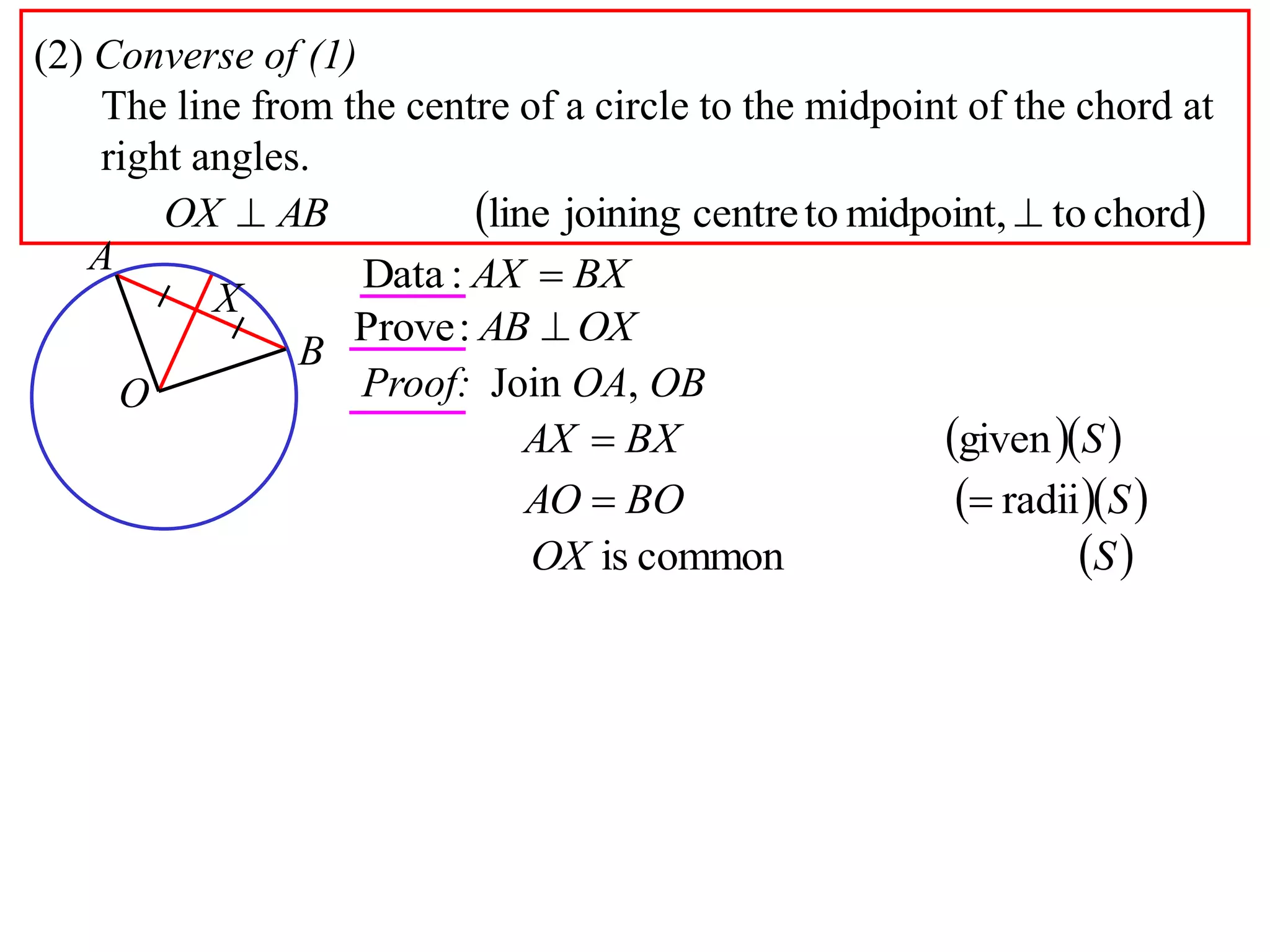
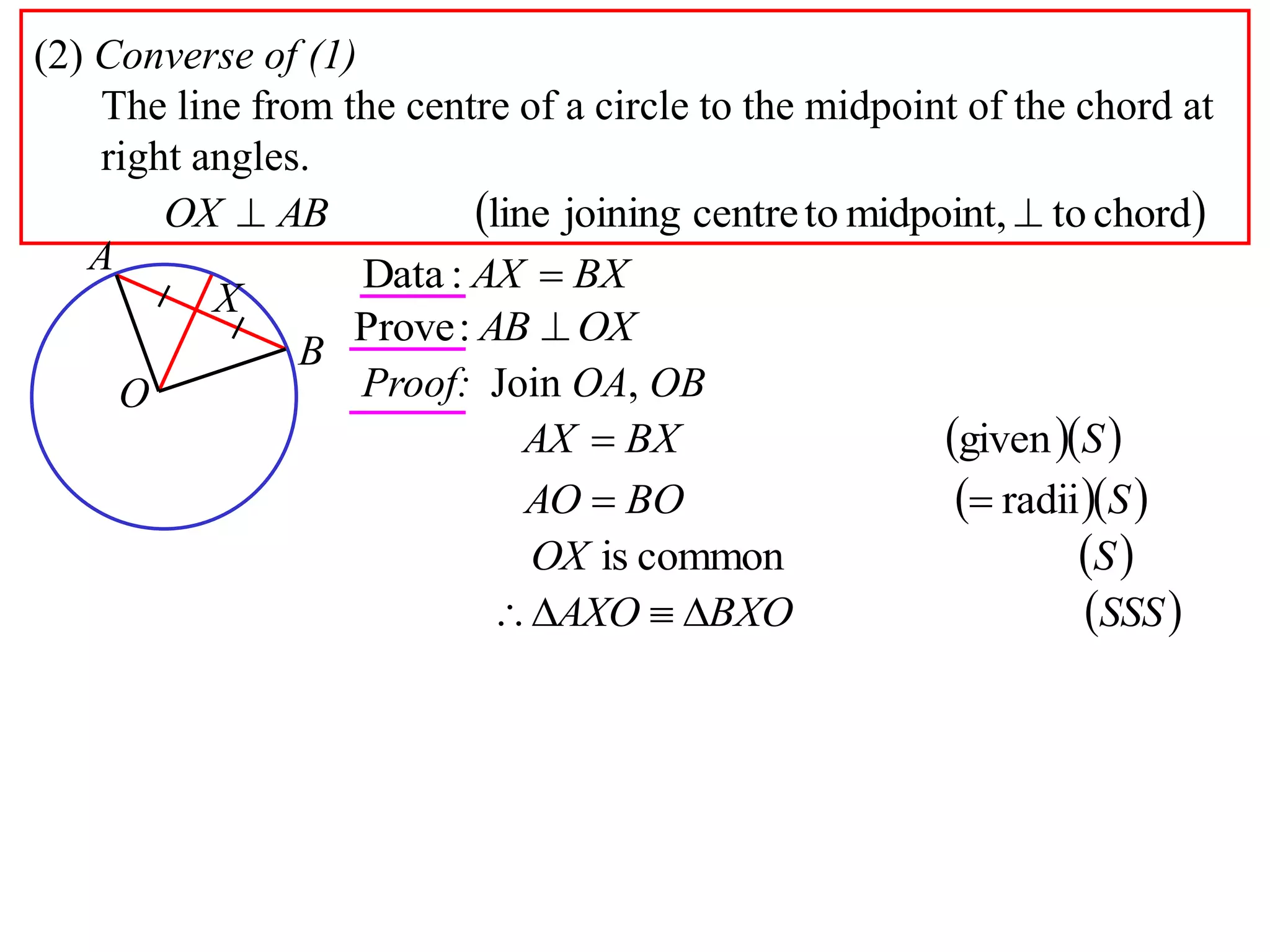
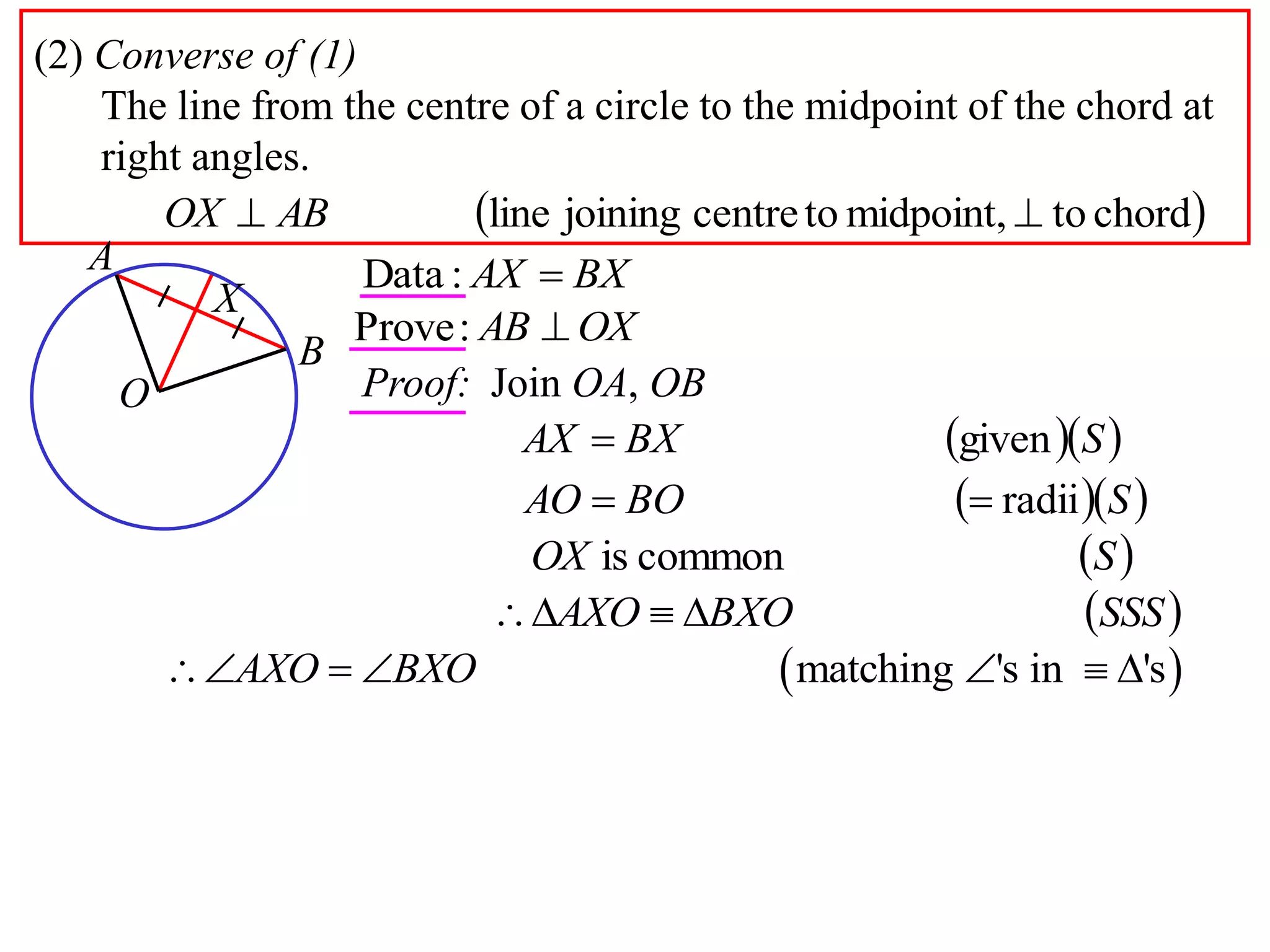
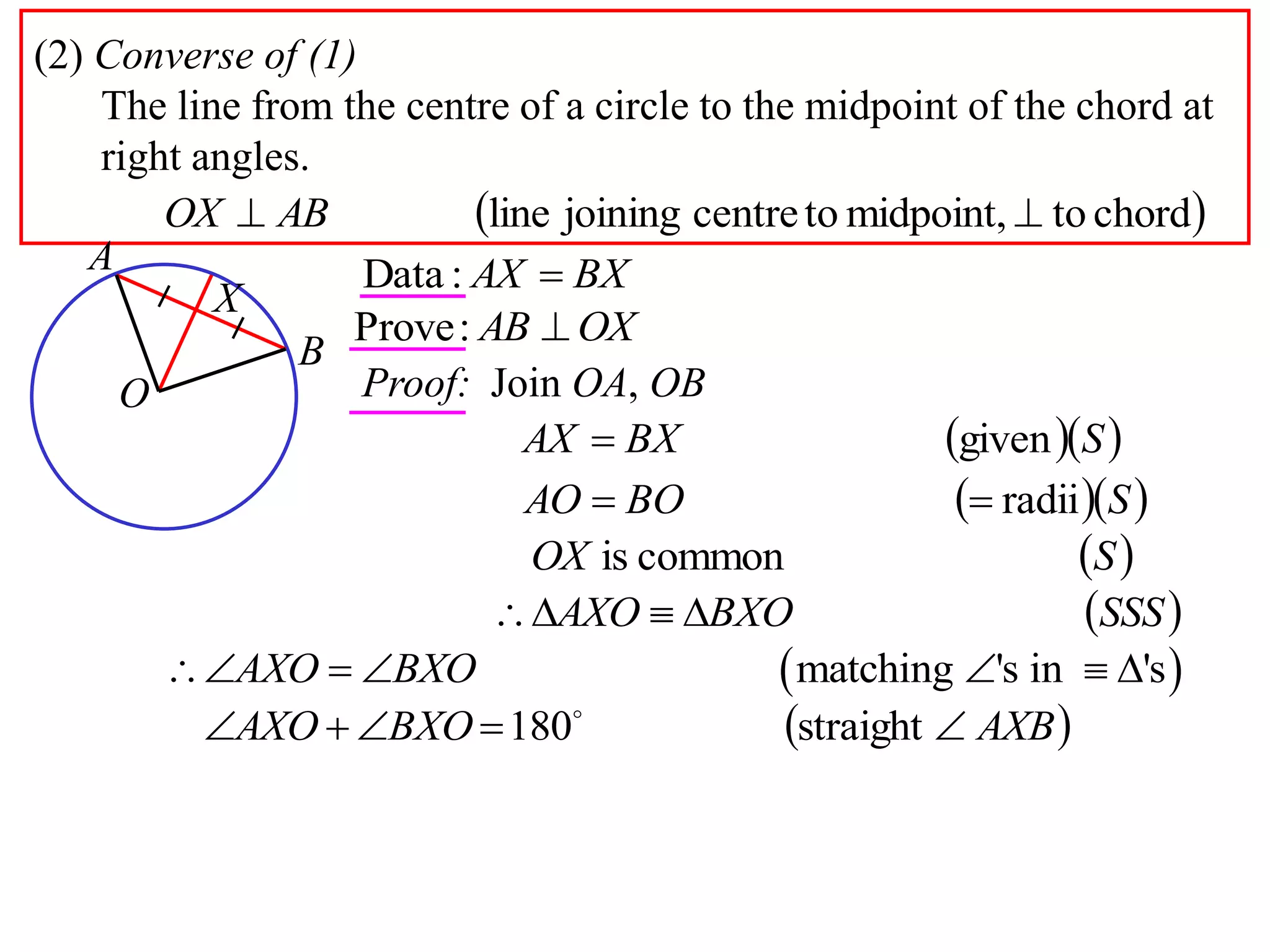
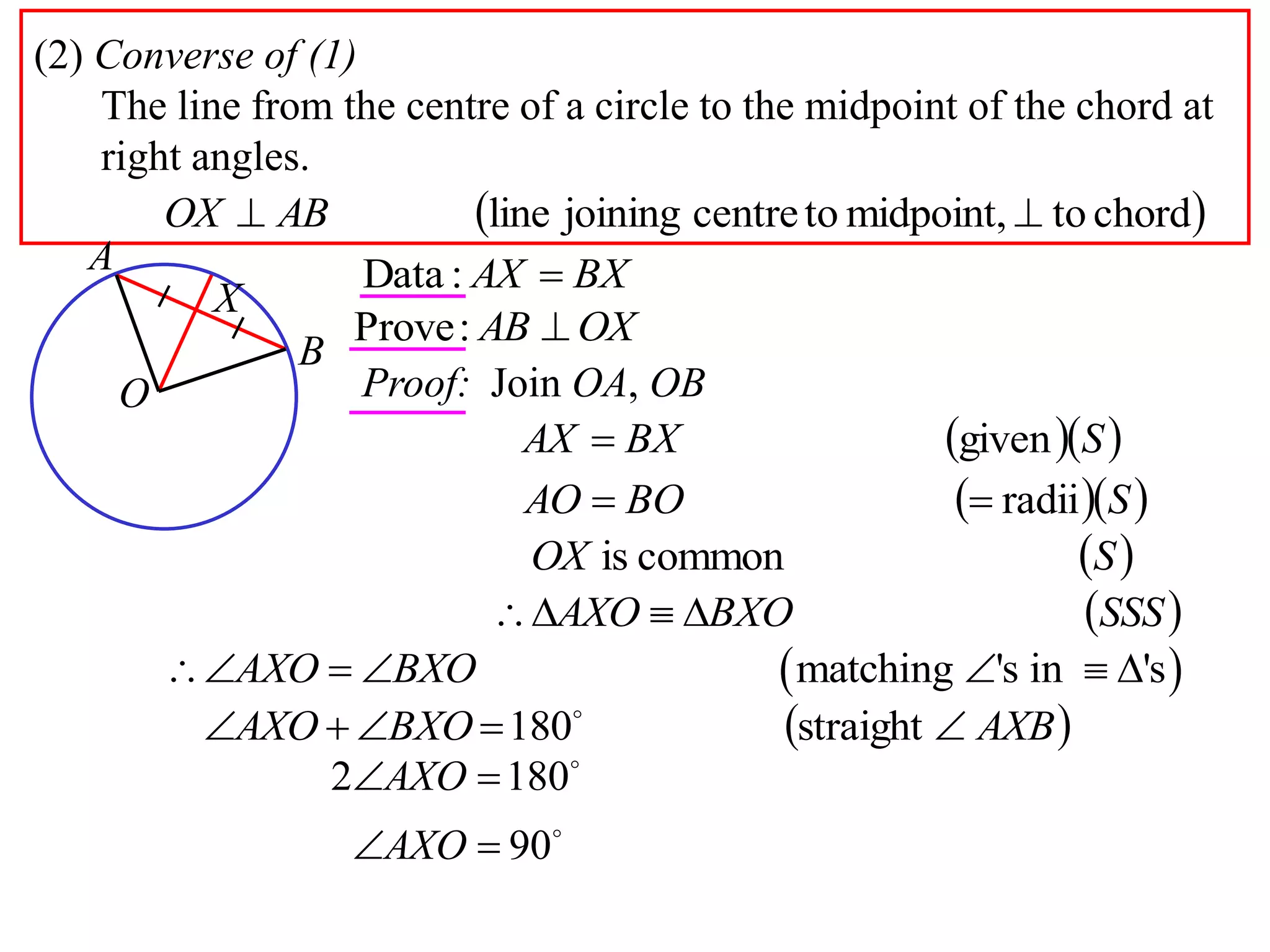
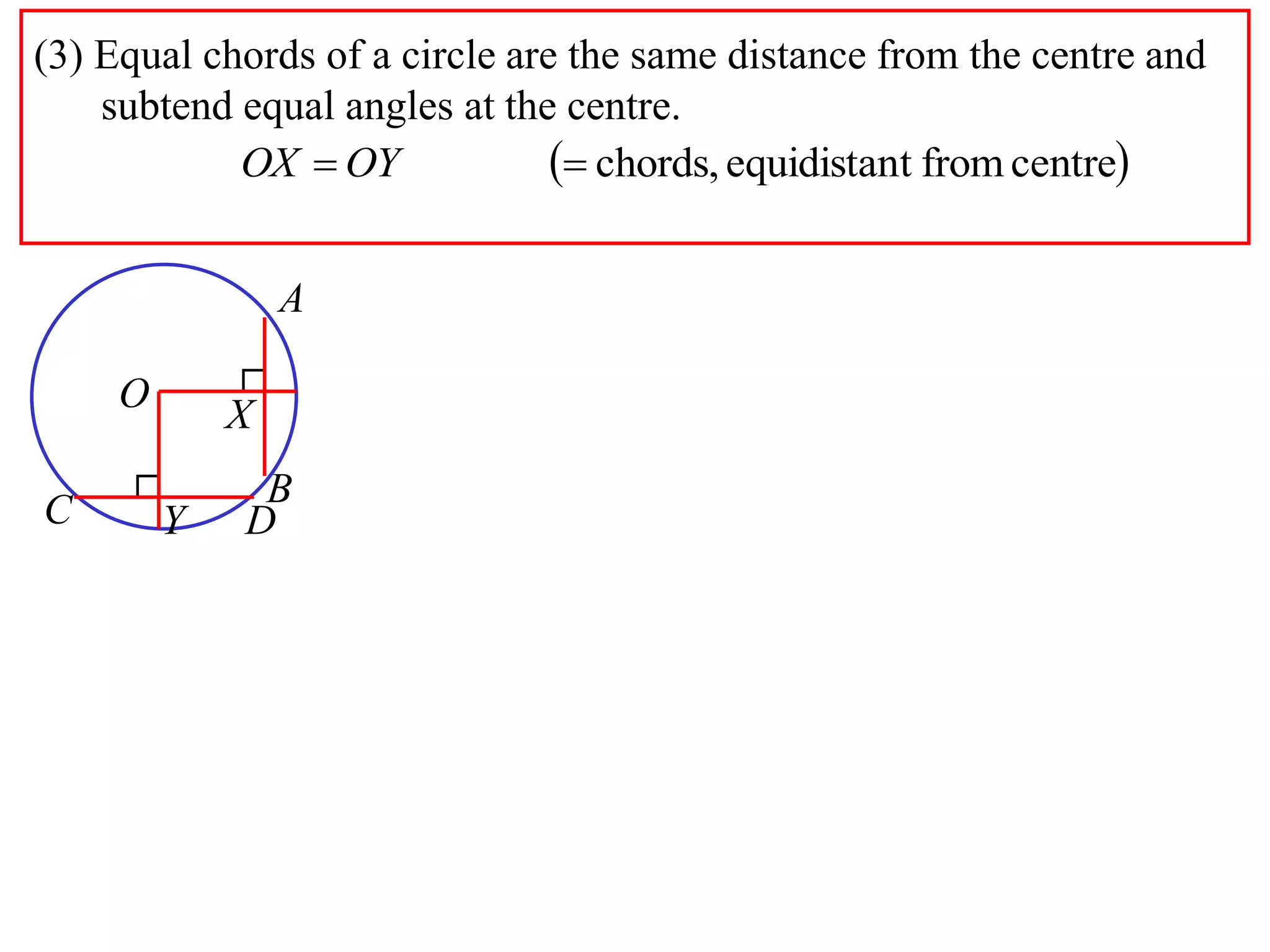
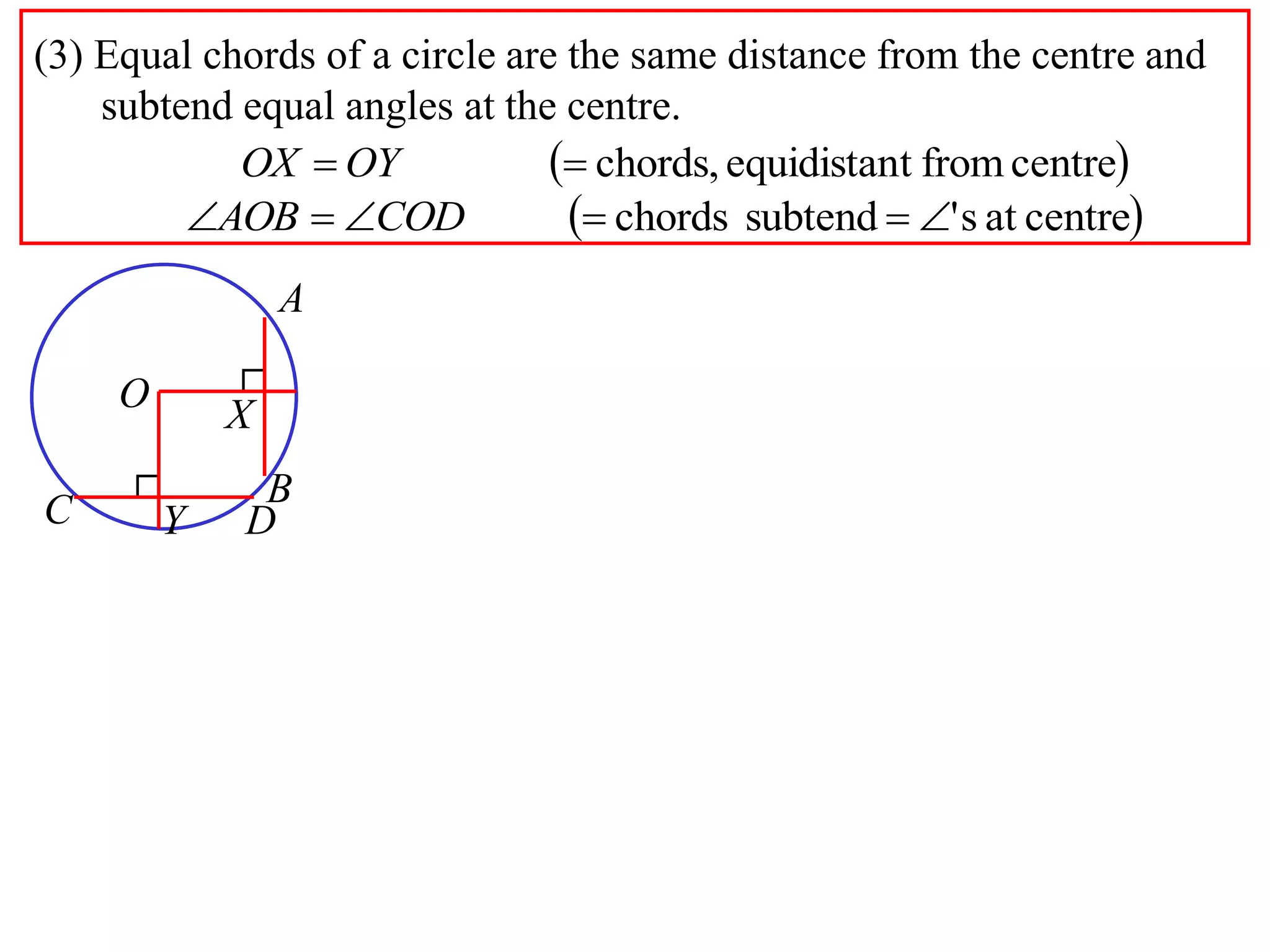
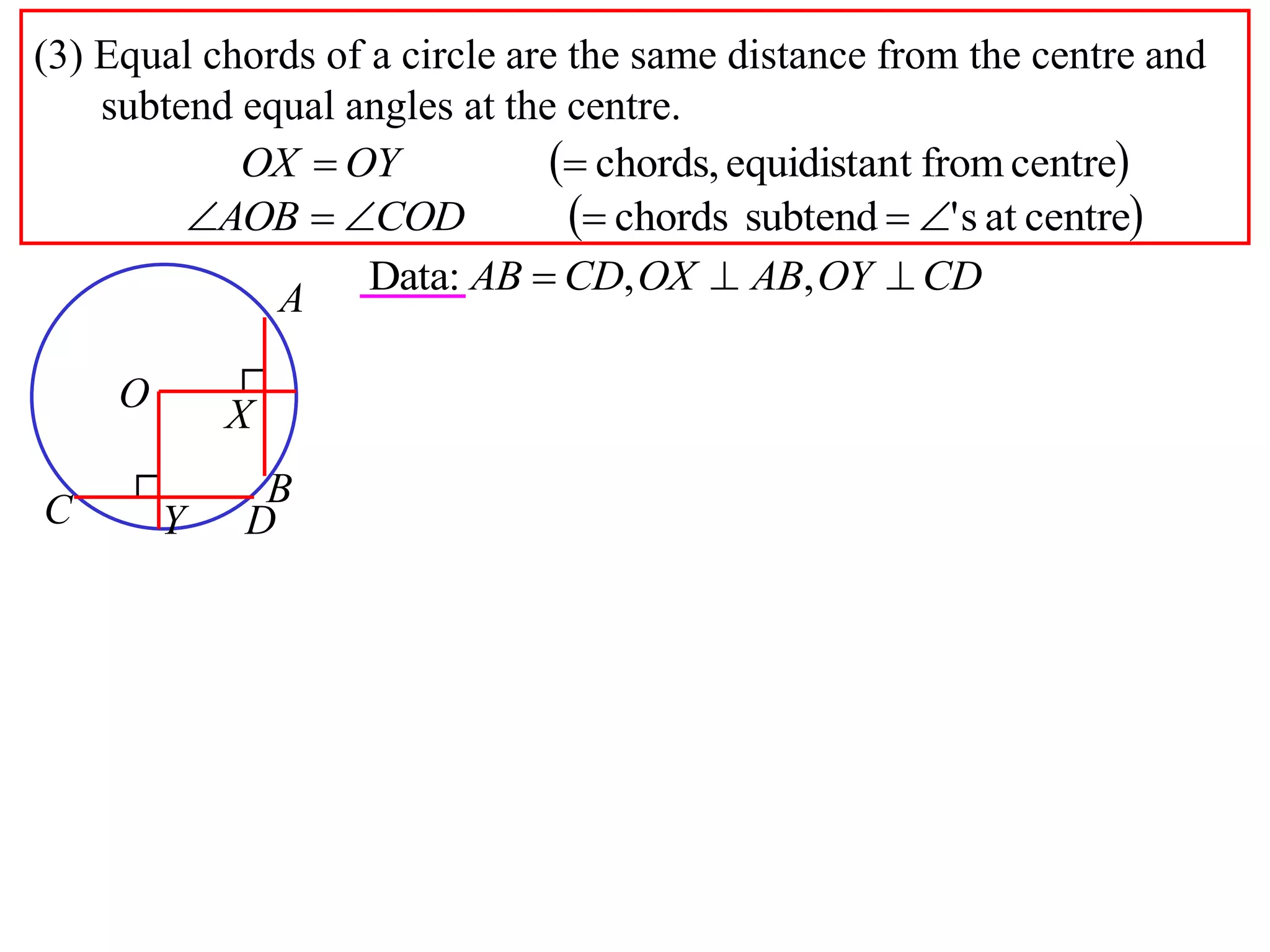
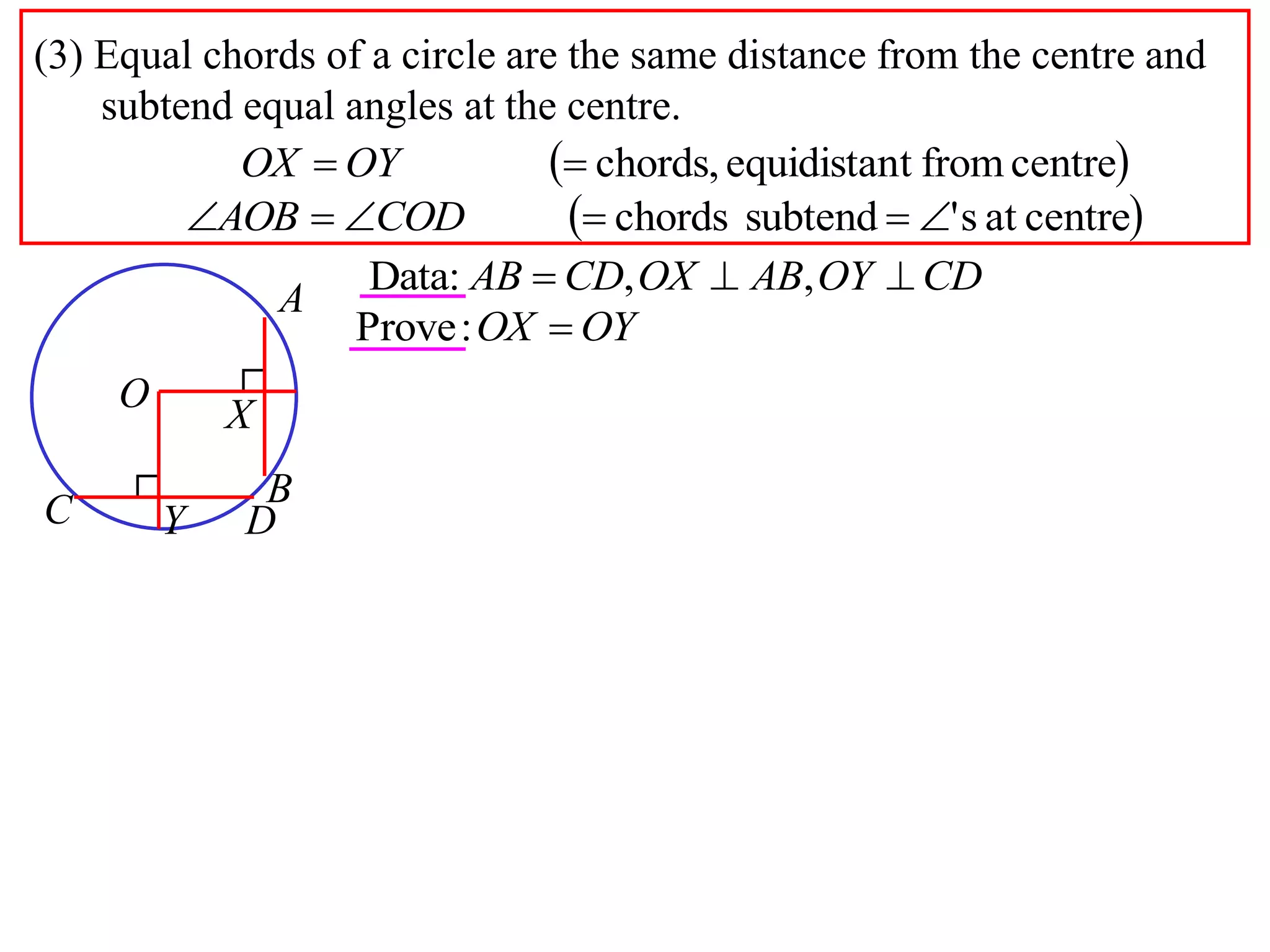
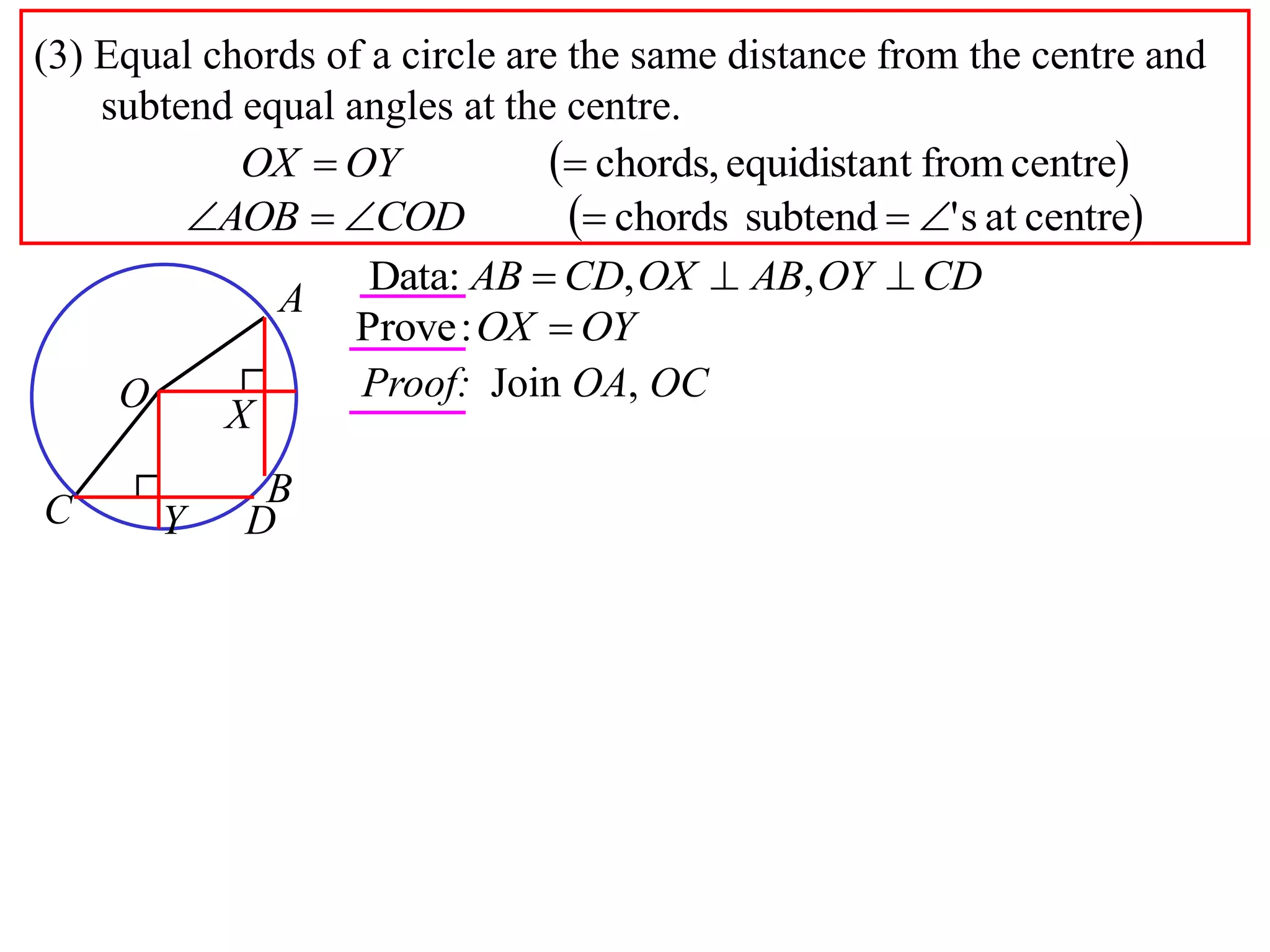
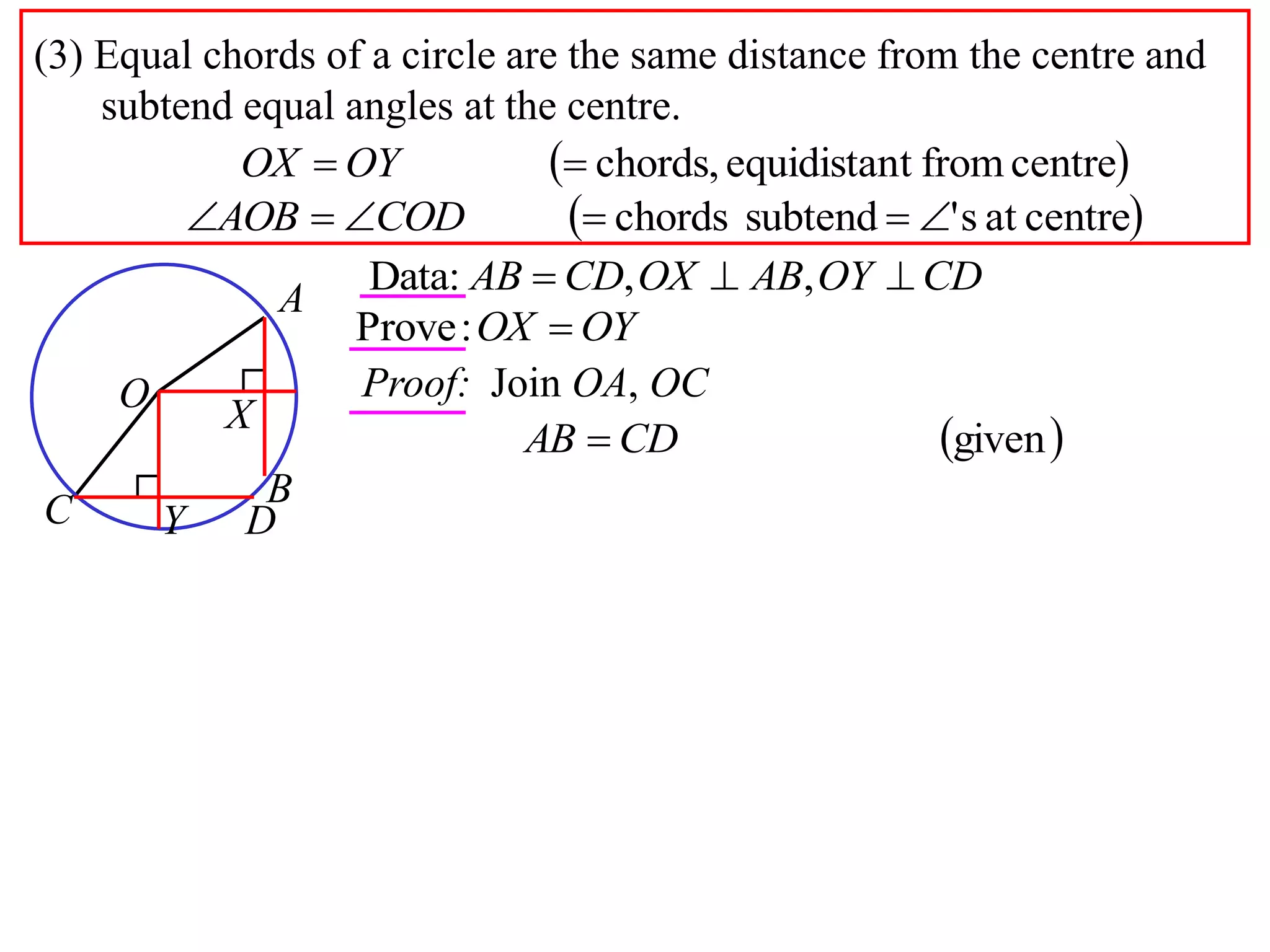
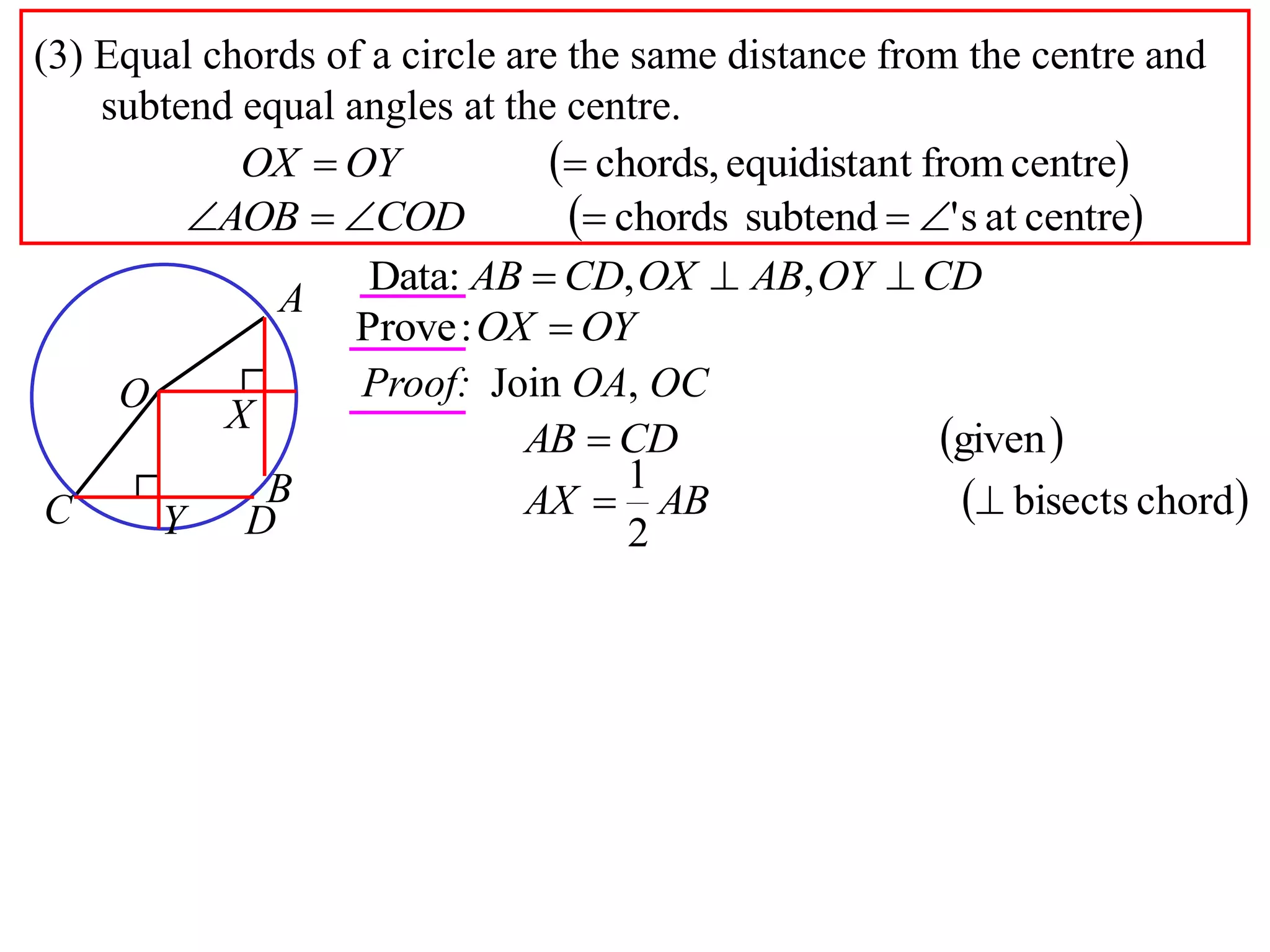
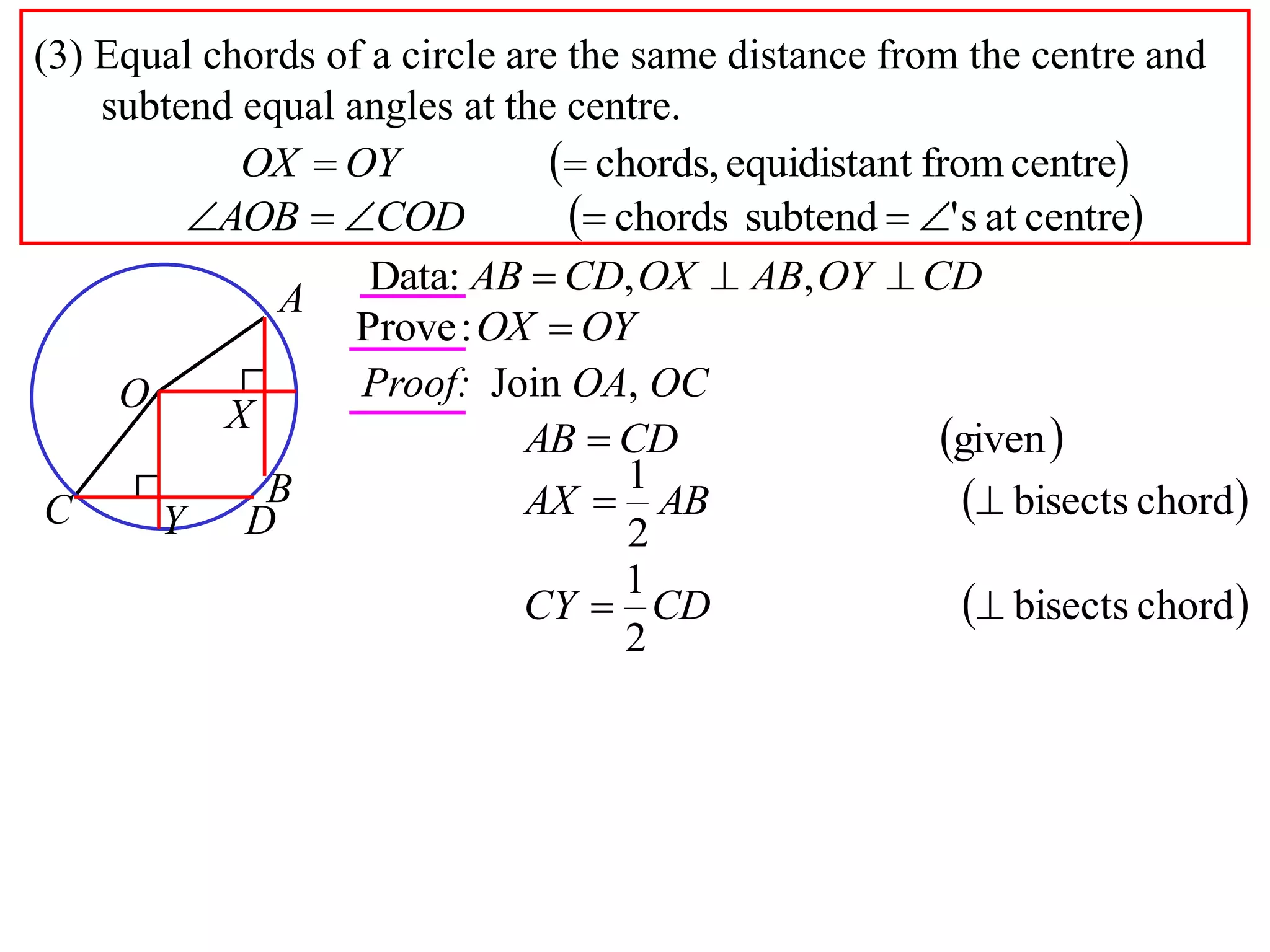
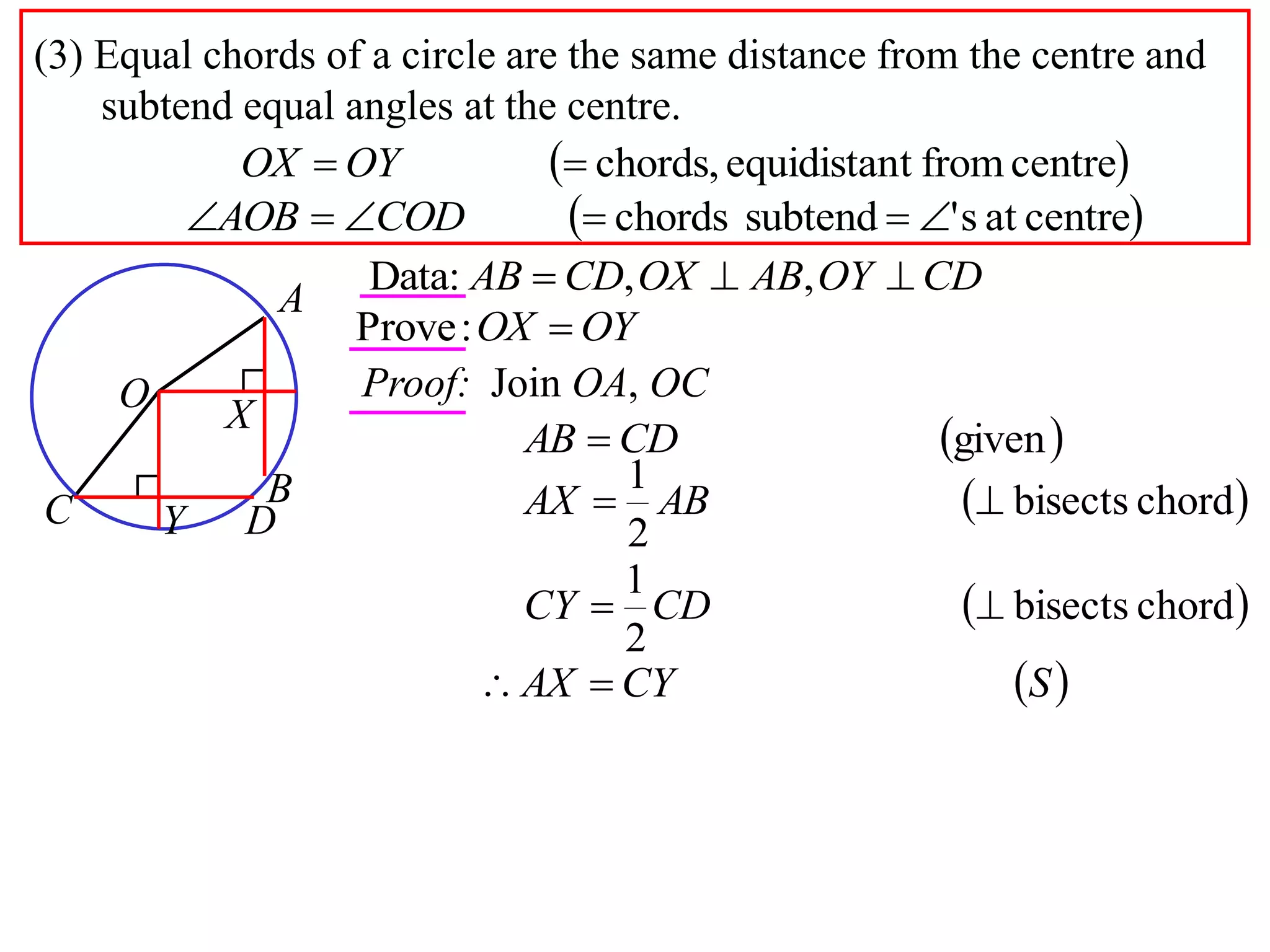
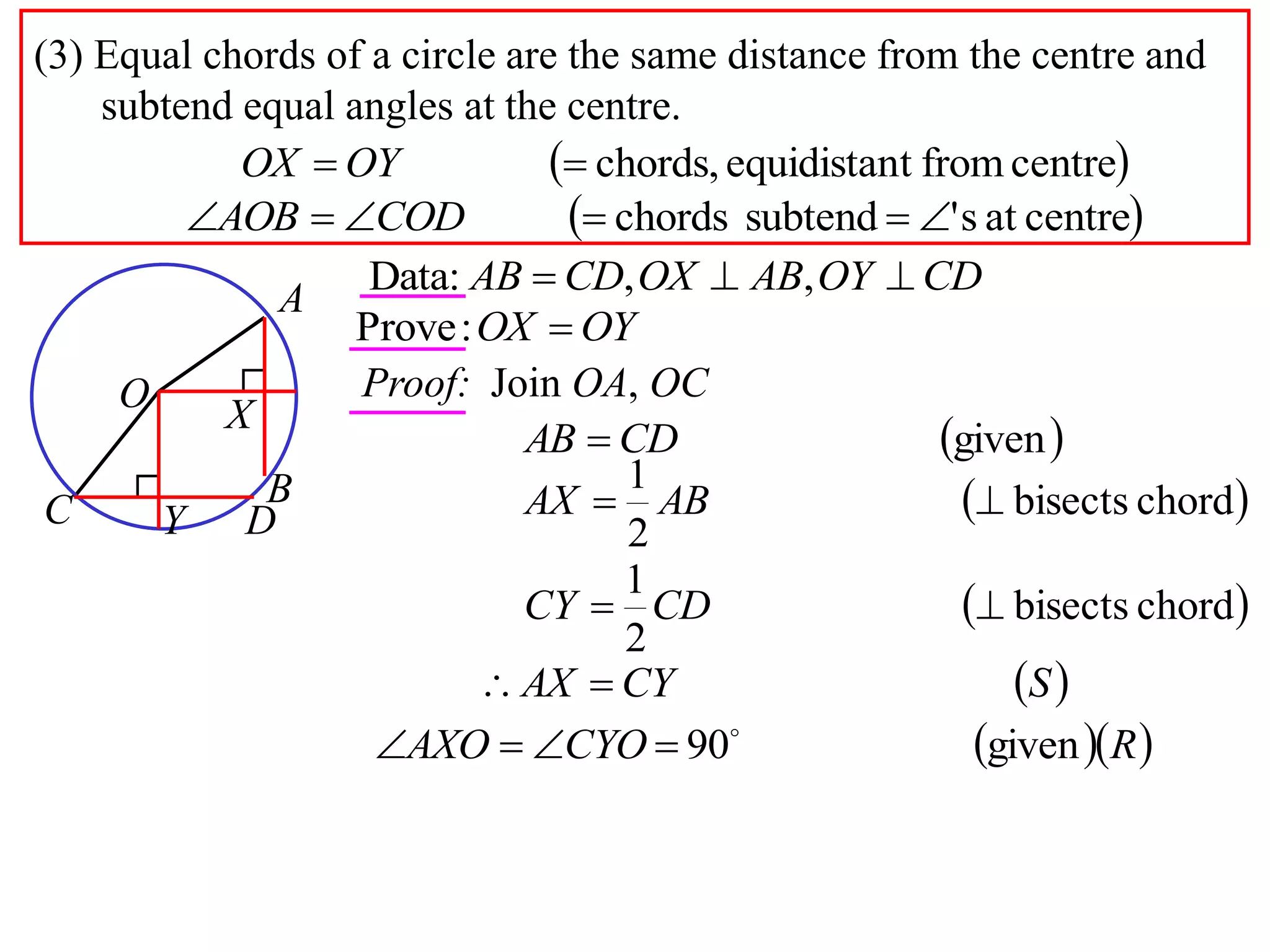
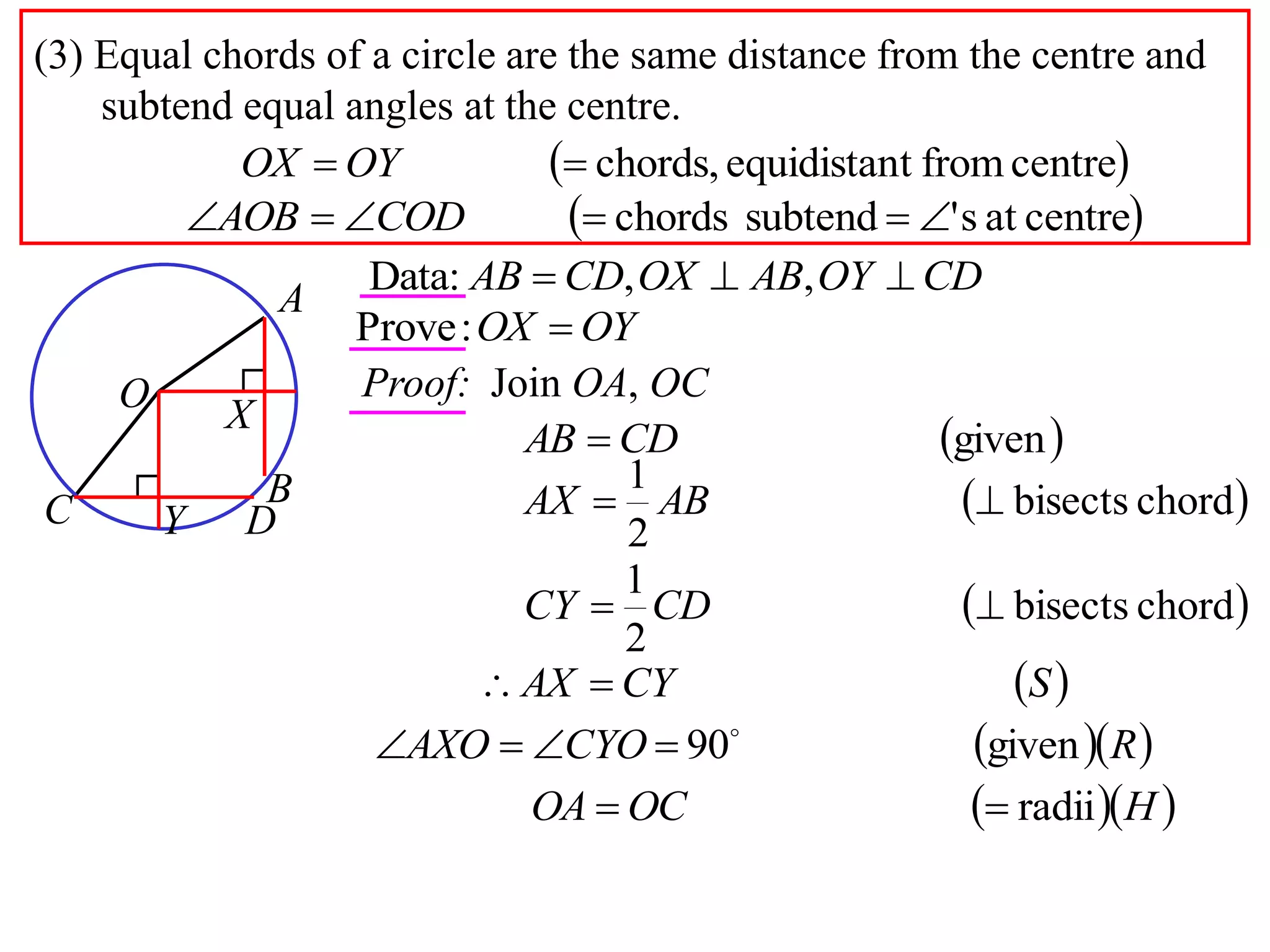
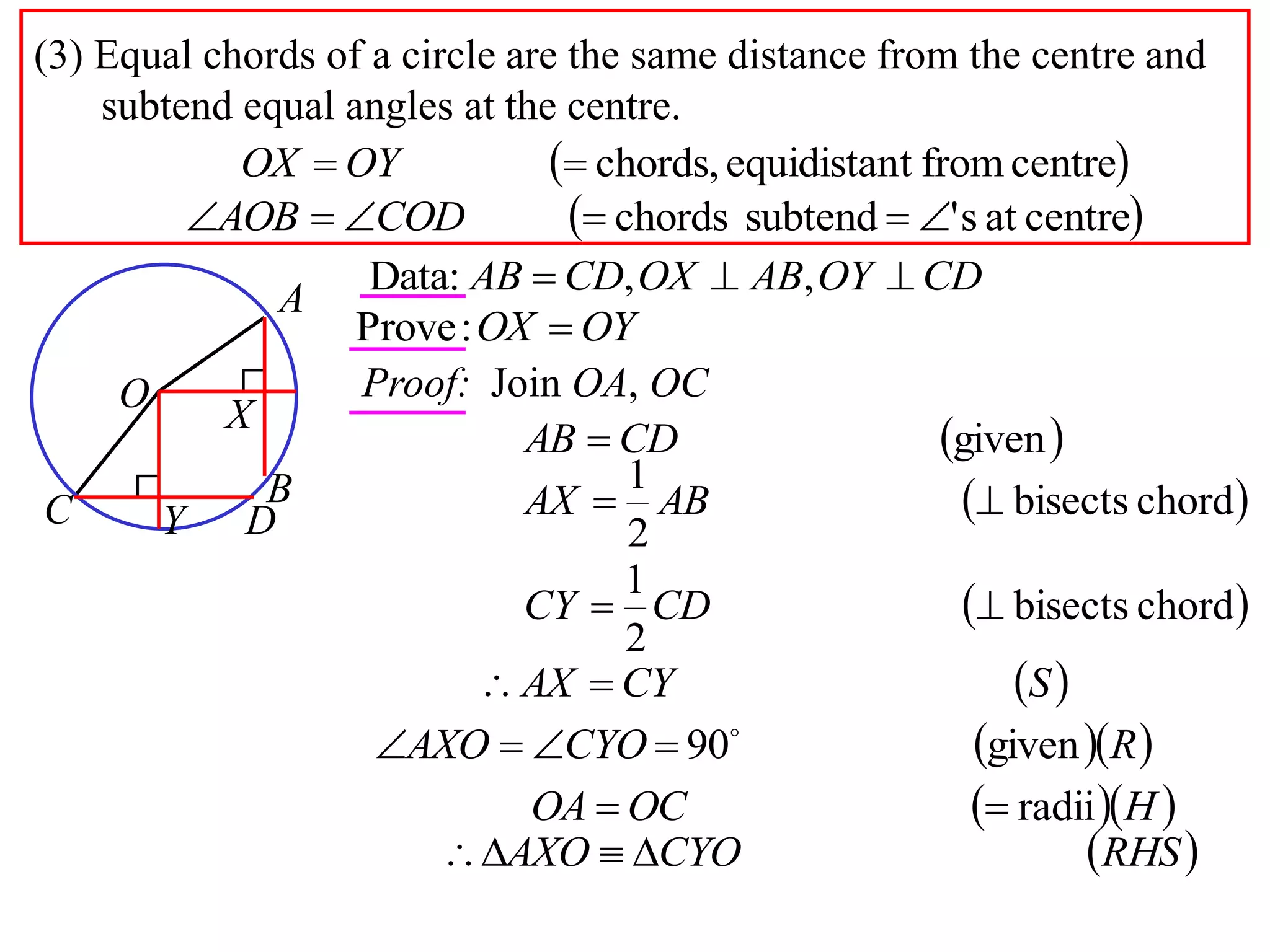
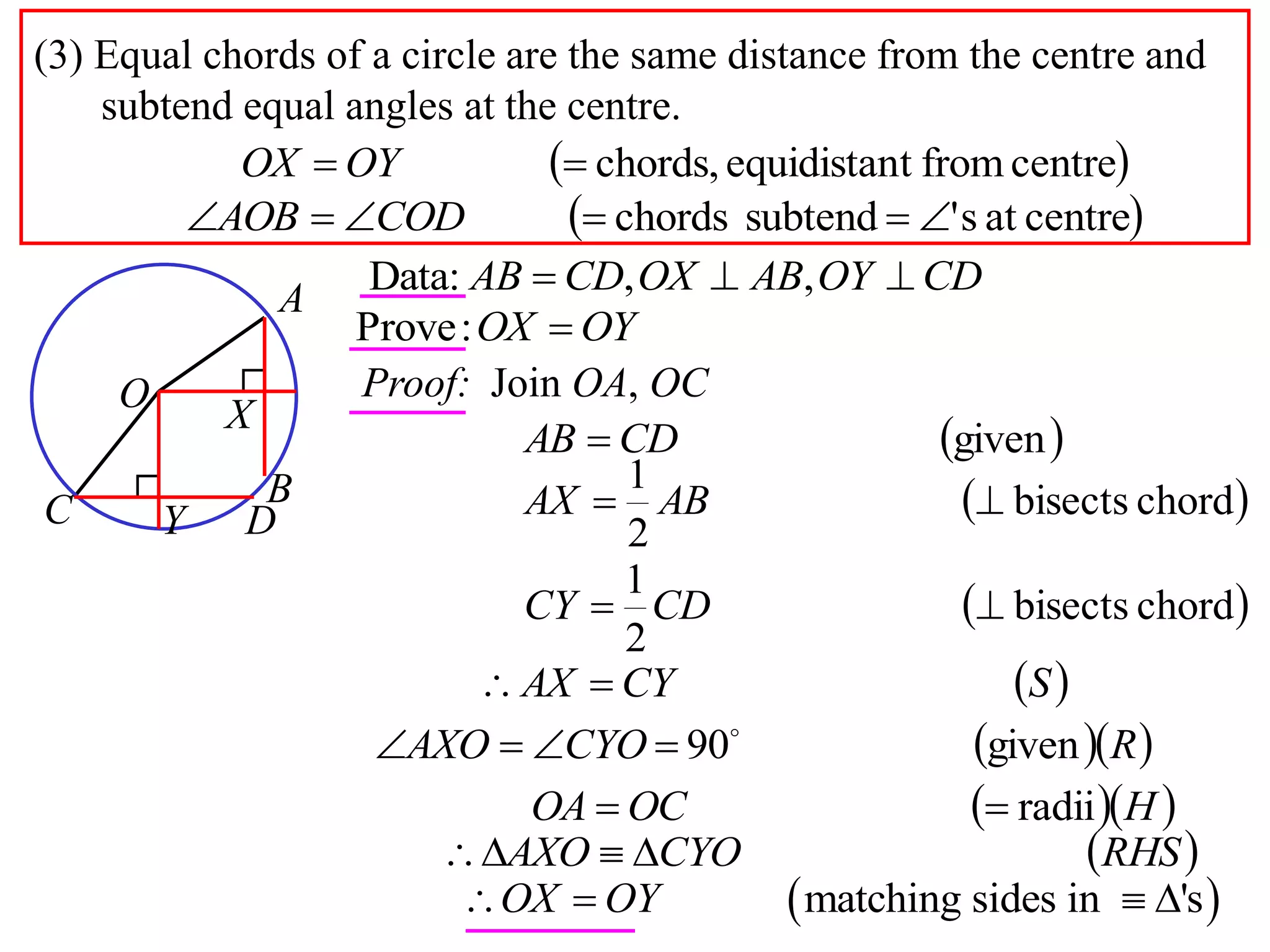
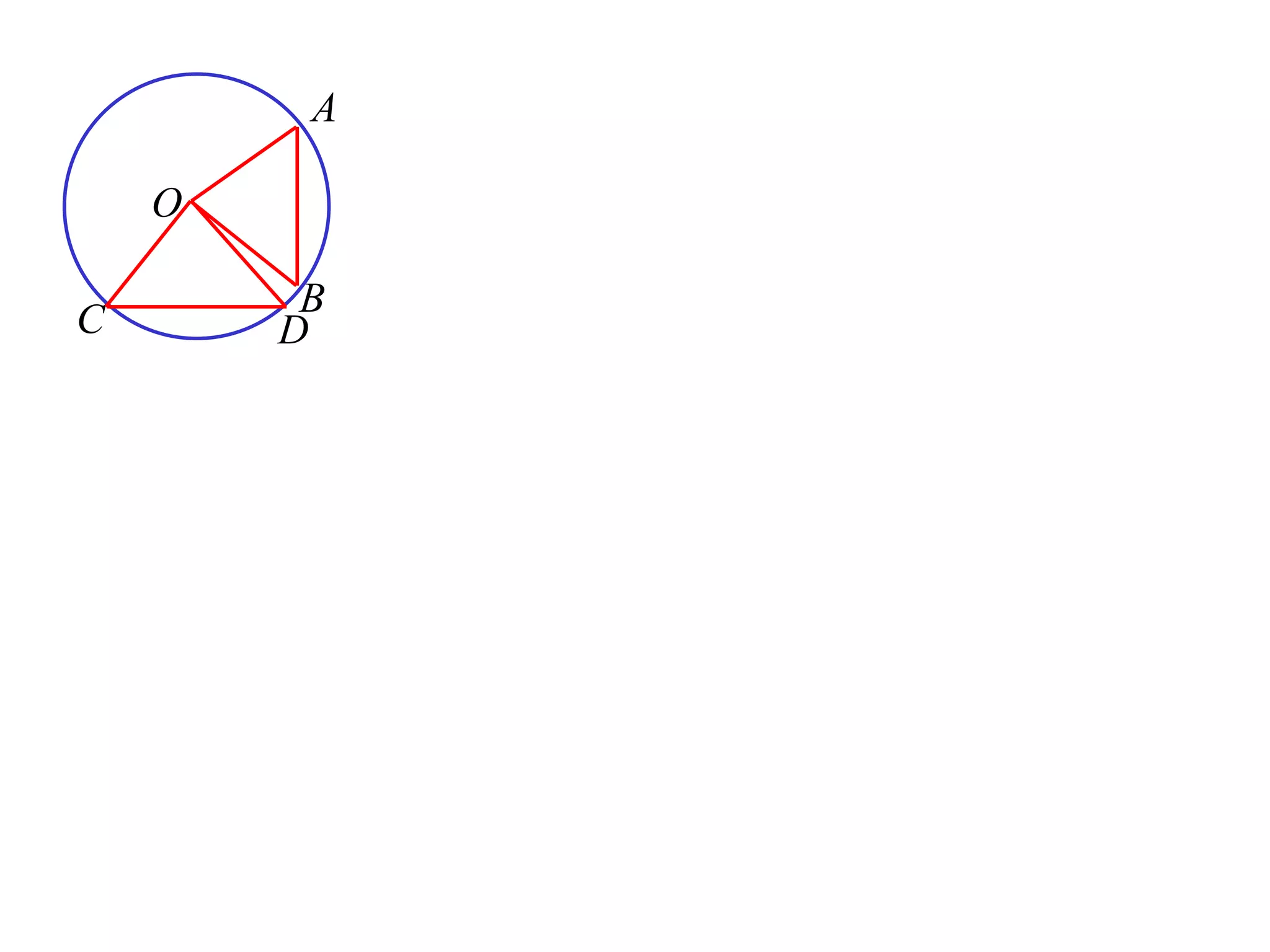
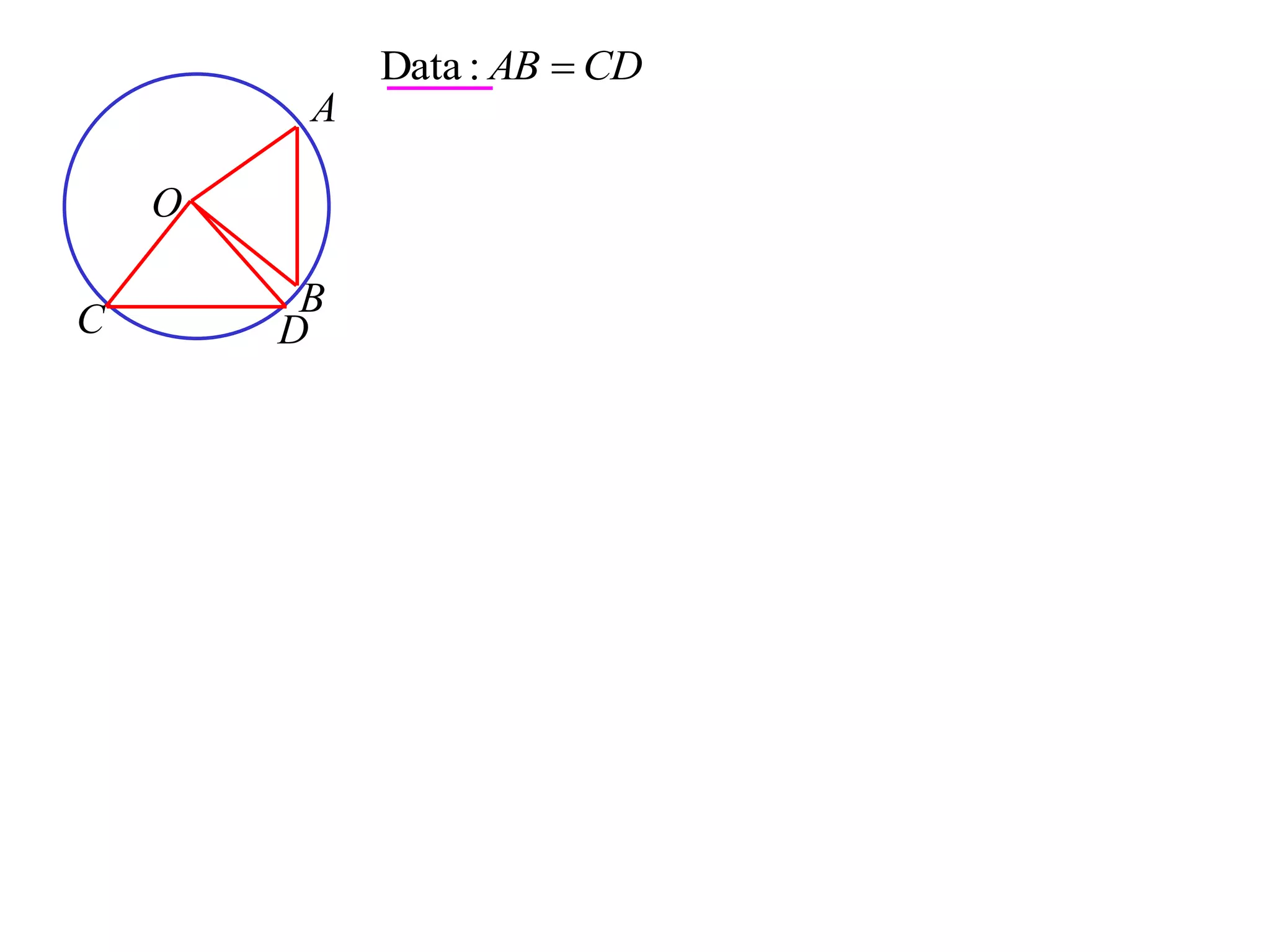
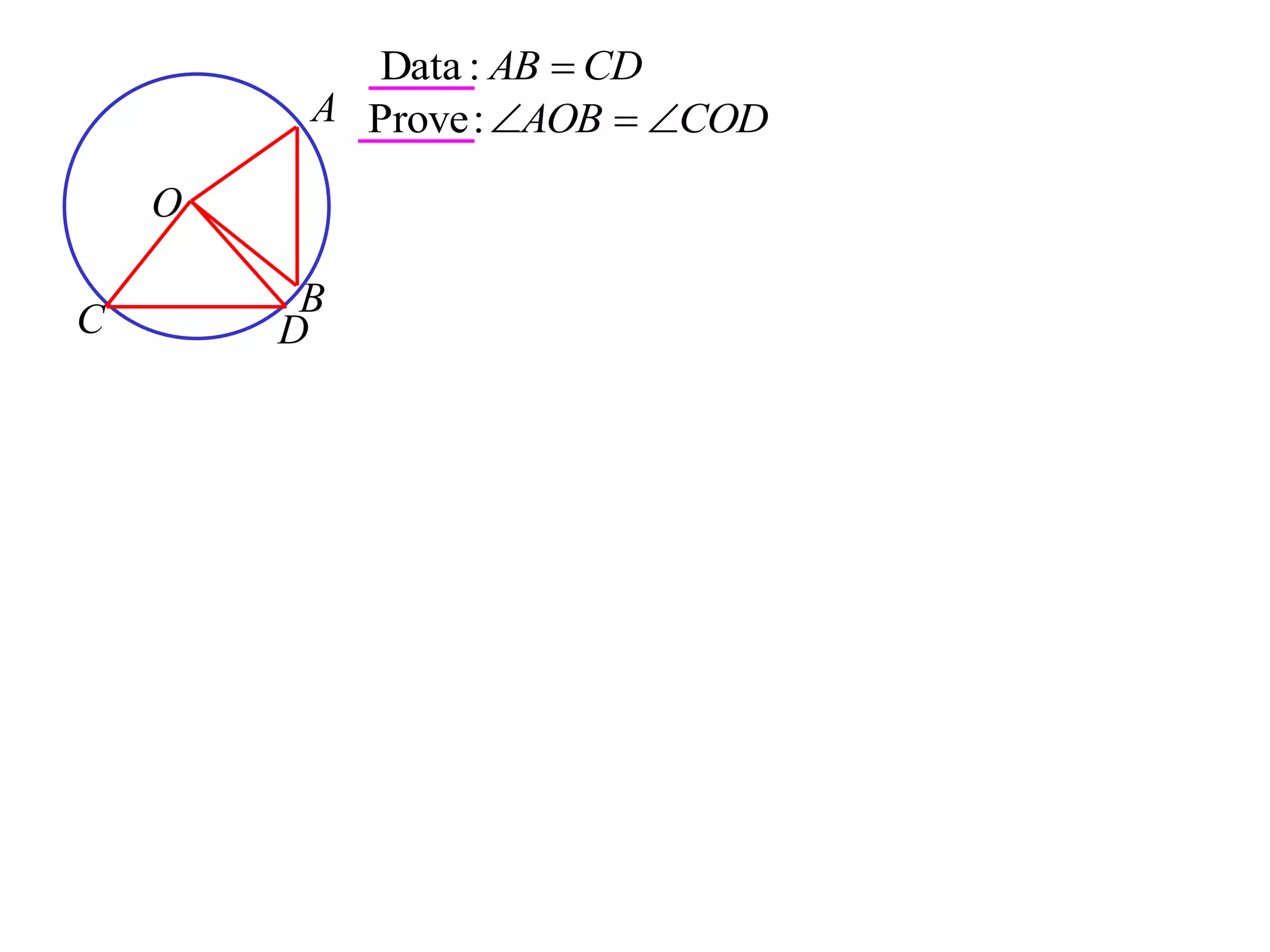
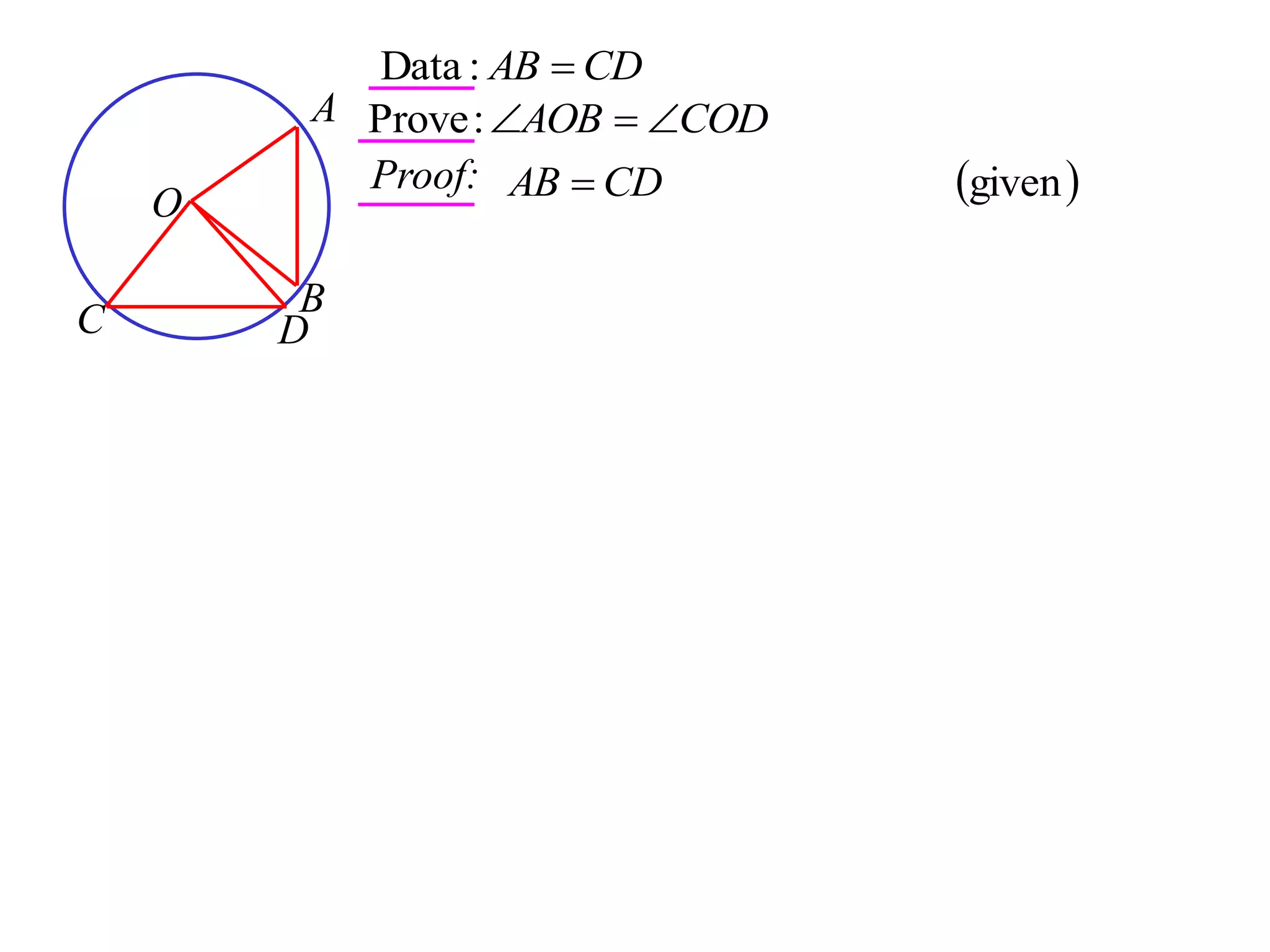
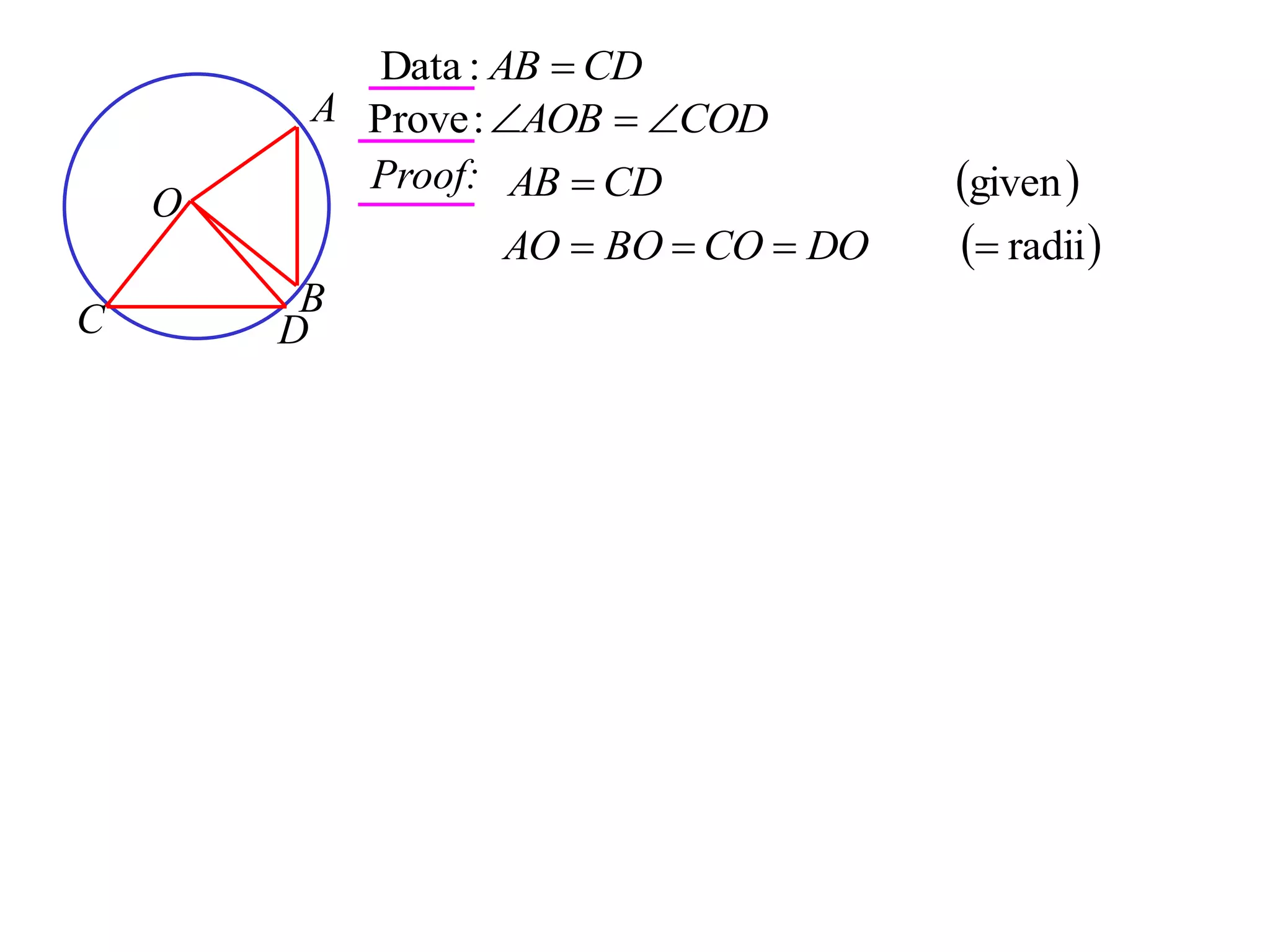
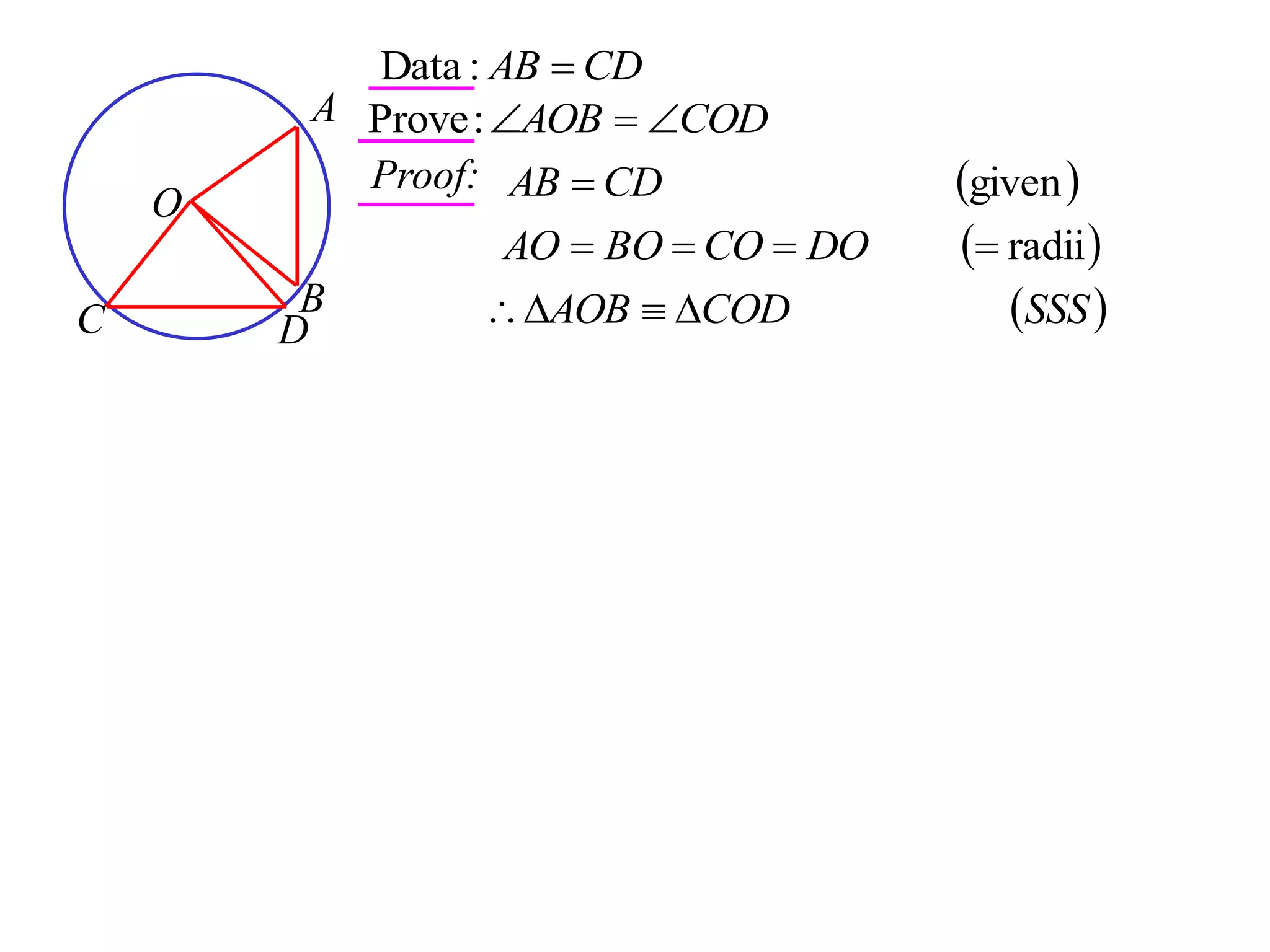
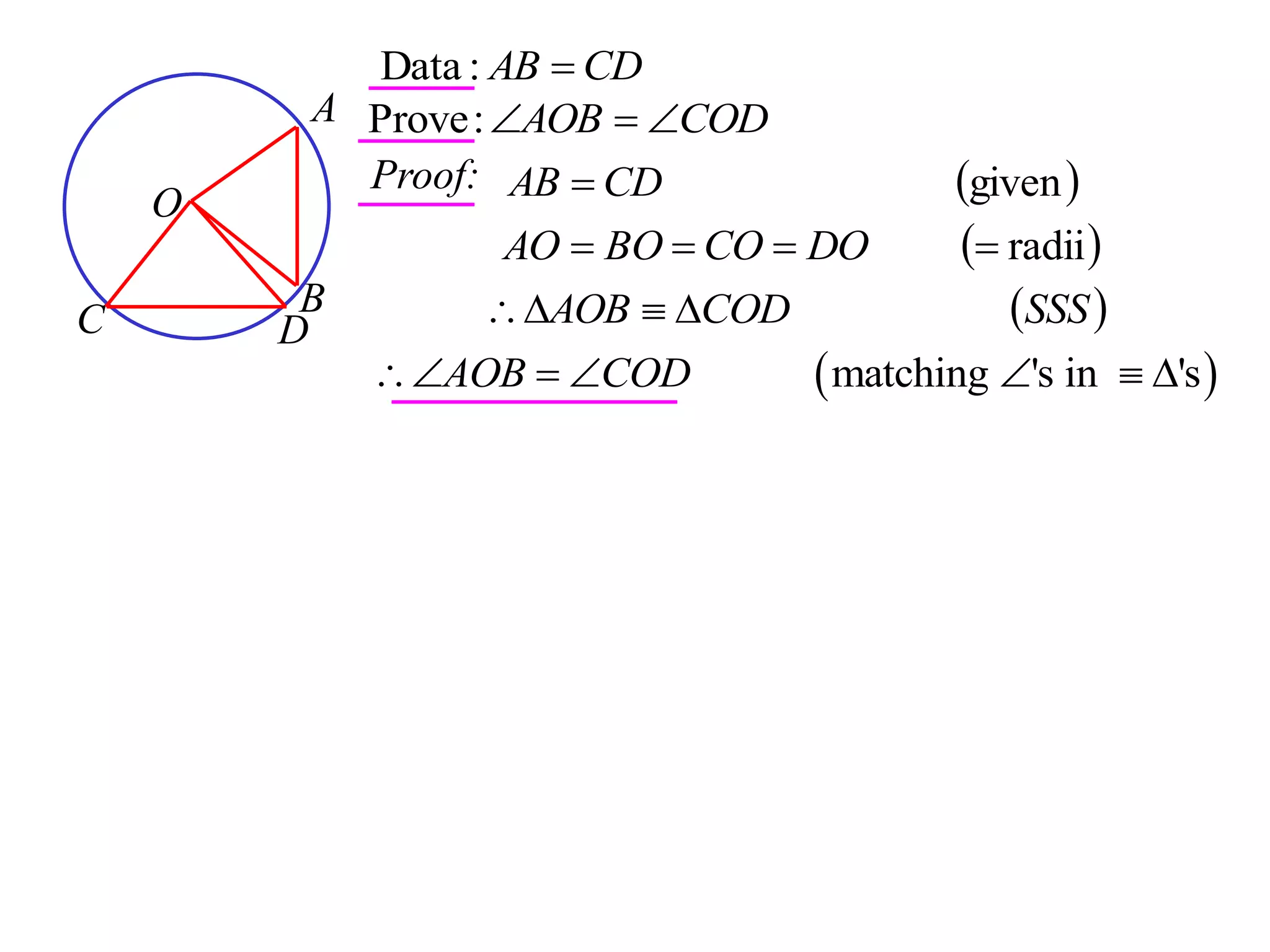
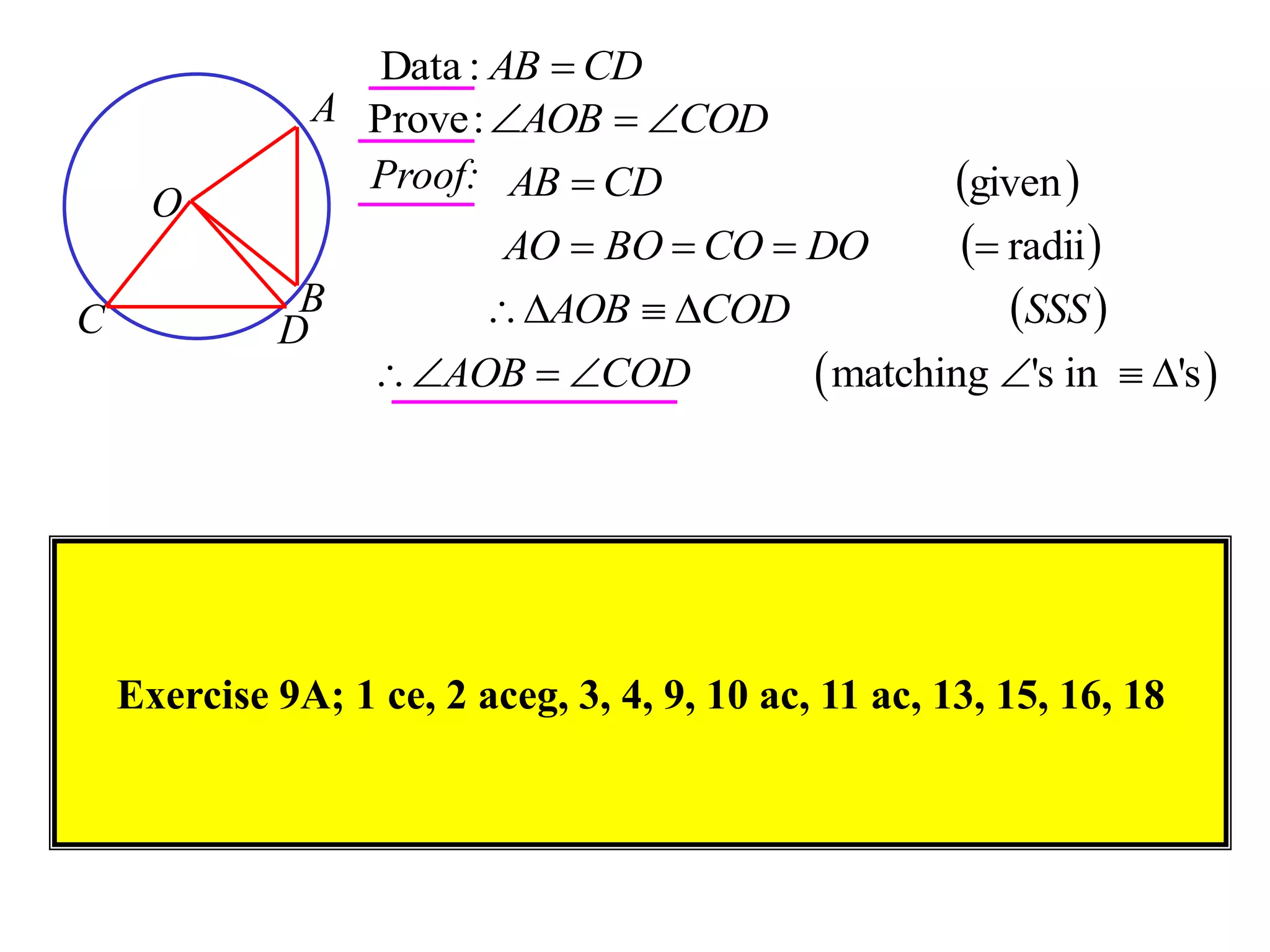
The document defines various terms related to circle geometry, including radius, diameter, chord, secant, tangent, arc, sector, segment, and concyclic points. It also presents two theorems about chords: 1) a perpendicular from the circle center to a chord bisects the chord, and 2) the converse - a line from the center to the midpoint of a chord is perpendicular to the chord. Diagrams and proofs of the theorems are provided.

1. Circle Geometry

2. Circle Geometry
Circle Geometry Definitions

3. Circle Geometry
Circle Geometry Definitions

4. Circle Geometry
Circle Geometry Definitions
Radius:an interval joining centre to the
circumference
radius

5. Circle Geometry
Circle Geometry Definitions
Radius:an interval joining centre to the
circumference
radius
Diameter:an interval passing through the
centre, joining any two points
on the circumference
diameter

6. Circle Geometry
Circle Geometry Definitions
Radius:an interval joining centre to the
circumference
radius
Diameter:an interval passing through the
centre, joining any two points
on the circumference
diameter Chord:an interval joining two points on
the circumference
chord

7. Circle Geometry
Circle Geometry Definitions
Radius:an interval joining centre to the
circumference
radius
Diameter:an interval passing through the
centre, joining any two points
on the circumference
diameter Chord:an interval joining two points on
the circumference
chord
Secant: a line that cuts the circle
secant

8. Circle Geometry
Circle Geometry Definitions
Radius:an interval joining centre to the
circumference
radius
Diameter:an interval passing through the
centre, joining any two points
on the circumference
diameter Chord:an interval joining two points on
the circumference
chord
Secant: a line that cuts the circle
secant
Tangent: a line that touches the circle
tangent

9. Circle Geometry
Circle Geometry Definitions
Radius:an interval joining centre to the
circumference
radius
Diameter:an interval passing through the
centre, joining any two points
on the circumference
diameter Chord:an interval joining two points on
the circumference
chord
Secant: a line that cuts the circle
secant
Tangent: a line that touches the circle
tangent Arc: a piece of the circumference
arc

11. Sector: a plane figure with two radii and an
arc as boundaries.
sector

12. Sector: a plane figure with two radii and an
arc as boundaries.
sector
The minor sector is the small “piece of the
pie”, the major sector is the large “piece”

13. Sector: a plane figure with two radii and an
arc as boundaries.
sector
The minor sector is the small “piece of the
pie”, the major sector is the large “piece”
A quadrant is a sector where the angle at
the centre is 90 degrees

14. Sector: a plane figure with two radii and an
arc as boundaries.
sector
The minor sector is the small “piece of the
pie”, the major sector is the large “piece”
A quadrant is a sector where the angle at
the centre is 90 degrees
Segment:a plane figure with a chord and an
arc as boundaries.
segment

15. Sector: a plane figure with two radii and an
arc as boundaries.
sector
The minor sector is the small “piece of the
pie”, the major sector is the large “piece”
A quadrant is a sector where the angle at
the centre is 90 degrees
Segment:a plane figure with a chord and an
arc as boundaries.
segment
A semicircle is a segment where the chord is
the diameter, it is also a sector as the diameter
is two radii.

17. Concyclic Points:points that lie on the same circle.
A
B
C
D

18. Concyclic Points:points that lie on the same circle.
concyclic points
A
B
C
D

19. Concyclic Points:points that lie on the same circle.
concyclic points
Cyclic Quadrilateral: a four sided shape with all vertices on the
same circle.
cyclic quadrilateral
A
B
C
D

21. A
B


22. A
B

 represents the angle
subtended at the centre by
the arc AB

23. A
B

 represents the angle
subtended at the centre by
the arc AB


24. A
B

 represents the angle
subtended at the centre by
the arc AB

 represents the angle
subtended at the
circumference by the arc AB

25. A
B

 represents the angle
subtended at the centre by
the arc AB

 represents the angle
subtended at the
circumference by the arc AB

26. A
B

 represents the angle
subtended at the centre by
the arc AB

 represents the angle
subtended at the
circumference by the arc AB
Concentric circles have the
same centre.

29. Circles touching internally
share a common tangent.

30. Circles touching internally
share a common tangent.
Circles touching externally
share a common tangent.

31. Circles touching internally
share a common tangent.
Circles touching externally
share a common tangent.

32. Circles touching internally
share a common tangent.
Circles touching externally
share a common tangent.

33. Chord (Arc) Theorems

34. Chord (Arc) Theorems
Note: = chords cut off = arcs

35. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.

36. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
A
B
O
X

37. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X

38. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data

39. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove

40. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove
Proof: Join OA, OB

41. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove
Proof: Join OA, OB
  RBXOAXO given90


42. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove
Proof: Join OA, OB
  RBXOAXO given90

  HBOAO radii

43. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove
Proof: Join OA, OB
  RBXOAXO given90

  HBOAO radii
 SOX commonis

44. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove
Proof: Join OA, OB
  RBXOAXO given90

  HBOAO radii
 SOX commonis
 RHSBXOAXO 

45. Chord (Arc) Theorems
Note: = chords cut off = arcs
(1) A perpendicular drawn to a chord from the centre of a circle bisects
the chord, and the perpendicular bisector of a chord passes through
the centre.
 chordbisectscentre,from BXAX
A
B
O
X
OXAB :Data
BXAX :Prove
Proof: Join OA, OB
  RBXOAXO given90

  HBOAO radii
 SOX commonis
 RHSBXOAXO 
 matching sides in 'sAX BX   

46. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.

47. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
A
B
O
X

48. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X

49. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data

50. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove

51. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB

52. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given

53. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii

54. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii
 SOX commonis

55. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii
 SOX commonis
 SSSBXOAXO 

56. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii
 SOX commonis
 SSSBXOAXO 
 matching 's in 'sAXO BXO     

57. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii
 SOX commonis
 SSSBXOAXO 
 matching 's in 'sAXO BXO     
 AXBBXOAXO straight180  

58. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii
 SOX commonis
 SSSBXOAXO 
 matching 's in 'sAXO BXO     
 AXBBXOAXO straight180  
90
1802




AXO
AXO

59. (2) Converse of (1)
The line from the centre of a circle to the midpoint of the chord at
right angles.
 chordtomidpoint,tocentrejoiningline  ABOX
A
B
O
X
BXAX :Data
OXAB :Prove
Proof: Join OA, OB
  SBXAX given
  SBOAO radii
 SOX commonis
 SSSBXOAXO 
 matching 's in 'sAXO BXO     
 AXBBXOAXO straight180  
90
1802




AXO
AXO
OXAB 

60. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.

61. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
A
B
O
X
C DY

62. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
A
B
O
X
C DY

63. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
 centreats'subtendchords  CODAOB
A
B
O
X
C DY

64. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
 centreats'subtendchords  CODAOB
A
B
O
X
C DY

65. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
 centreats'subtendchords  CODAOB
A
B
O
X
C DY

66. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 centreats'subtendchords  CODAOB
A
B
O
X
C DY

67. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 centreats'subtendchords  CODAOB
A
B
O
X
C DY

68. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 centreats'subtendchords  CODAOB
A
B
O
X
C DY

69. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 centreats'subtendchords  CODAOB
 chordbisects
2
1
 CDCY
A
B
O
X
C DY

70. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 SCYAX 
 centreats'subtendchords  CODAOB
 chordbisects
2
1
 CDCY
A
B
O
X
C DY

71. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 SCYAX 
  RCYOAXO given90

 centreats'subtendchords  CODAOB
 chordbisects
2
1
 CDCY
A
B
O
X
C DY

72. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 SCYAX 
  RCYOAXO given90

 centreats'subtendchords  CODAOB
 chordbisects
2
1
 CDCY
  HOCOA radii
A
B
O
X
C DY

73. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 SCYAX 
  RCYOAXO given90

 centreats'subtendchords  CODAOB
 chordbisects
2
1
 CDCY
  HOCOA radii
 RHSCYOAXO 
A
B
O
X
C DY

74. (3) Equal chords of a circle are the same distance from the centre and
subtend equal angles at the centre.
 centrefromtequidistanchords, OYOX
Data: , ,AB CD OX AB OY CD  
OYOX :Prove
Proof: Join OA, OC
 givenCDAB 
 chordbisects
2
1
 ABAX
 SCYAX 
  RCYOAXO given90

 matching sides in 'sOX OY   
 centreats'subtendchords  CODAOB
 chordbisects
2
1
 CDCY
  HOCOA radii
 RHSCYOAXO 
A
B
O
X
C DY

75. A
B
O
C D

76. A
B
O
C D
CDAB :Data

77. A
B
O
C D
CDAB :Data
CODAOB :Prove

78. A
B
O
C D
CDAB :Data
CODAOB :Prove
Proof:  givenCDAB 

79. A
B
O
C D
CDAB :Data
CODAOB :Prove
Proof:  givenCDAB 
 radii DOCOBOAO

80. A
B
O
C D
CDAB :Data
CODAOB :Prove
Proof:  givenCDAB 
 radii DOCOBOAO
 SSSCODAOB 

81. A
B
O
C D
CDAB :Data
CODAOB :Prove
Proof:  givenCDAB 
 radii DOCOBOAO
 matching 's in 'sAOB COD     
 SSSCODAOB 

82. A
B
O
C D
CDAB :Data
CODAOB :Prove
Proof:  givenCDAB 
 radii DOCOBOAO
 matching 's in 'sAOB COD     
 SSSCODAOB 
Exercise 9A; 1 ce, 2 aceg, 3, 4, 9, 10 ac, 11 ac, 13, 15, 16, 18