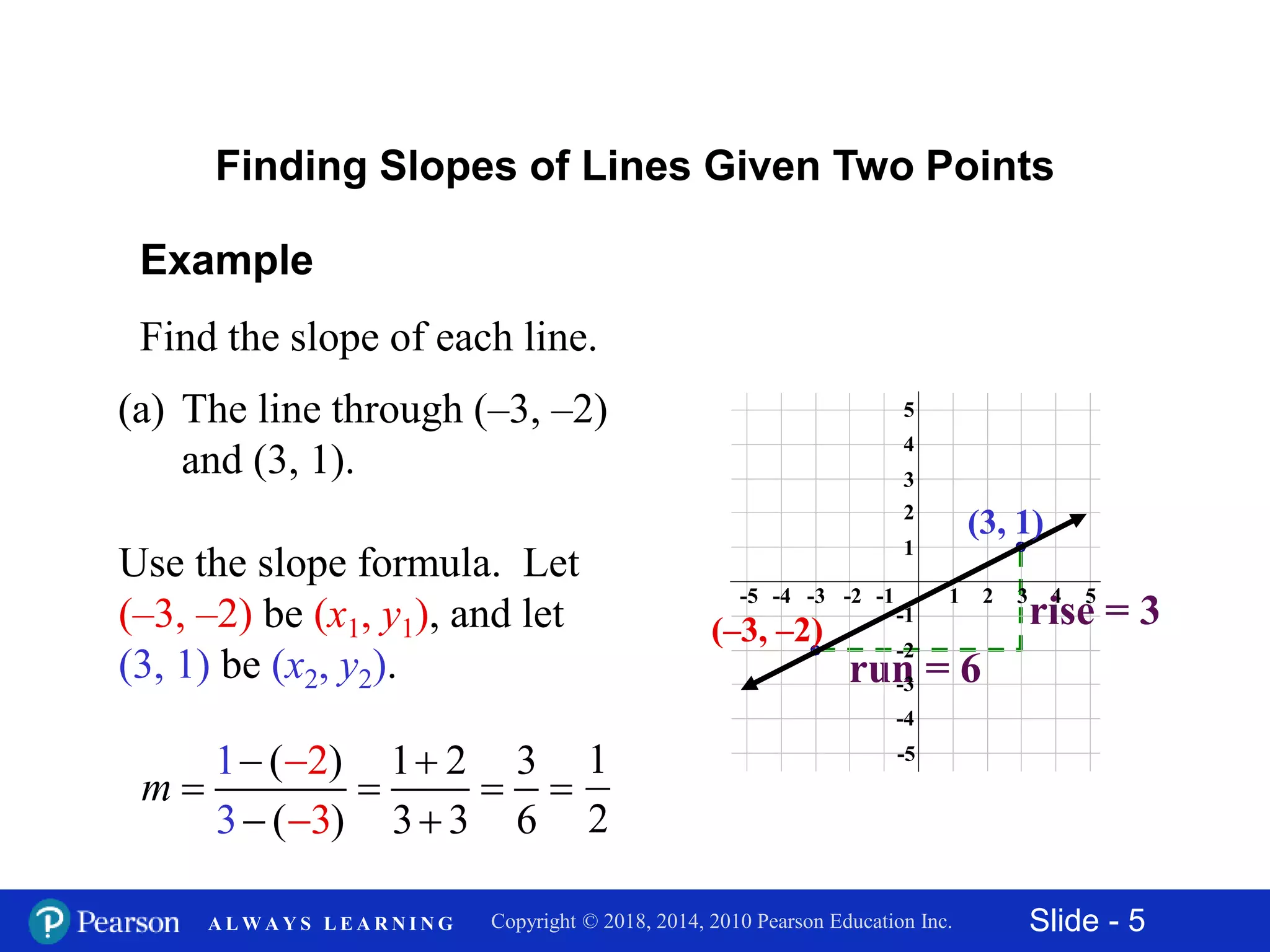
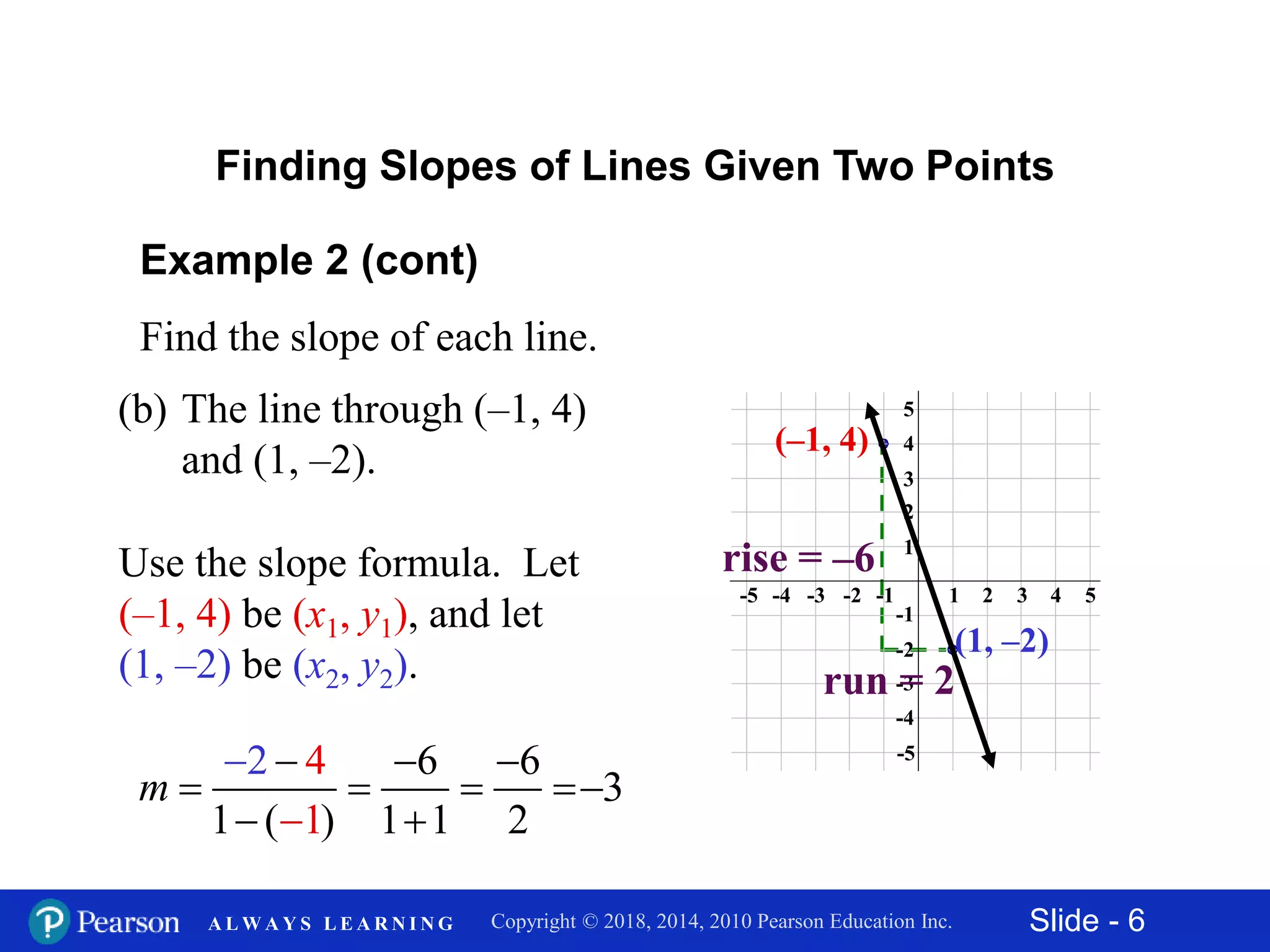
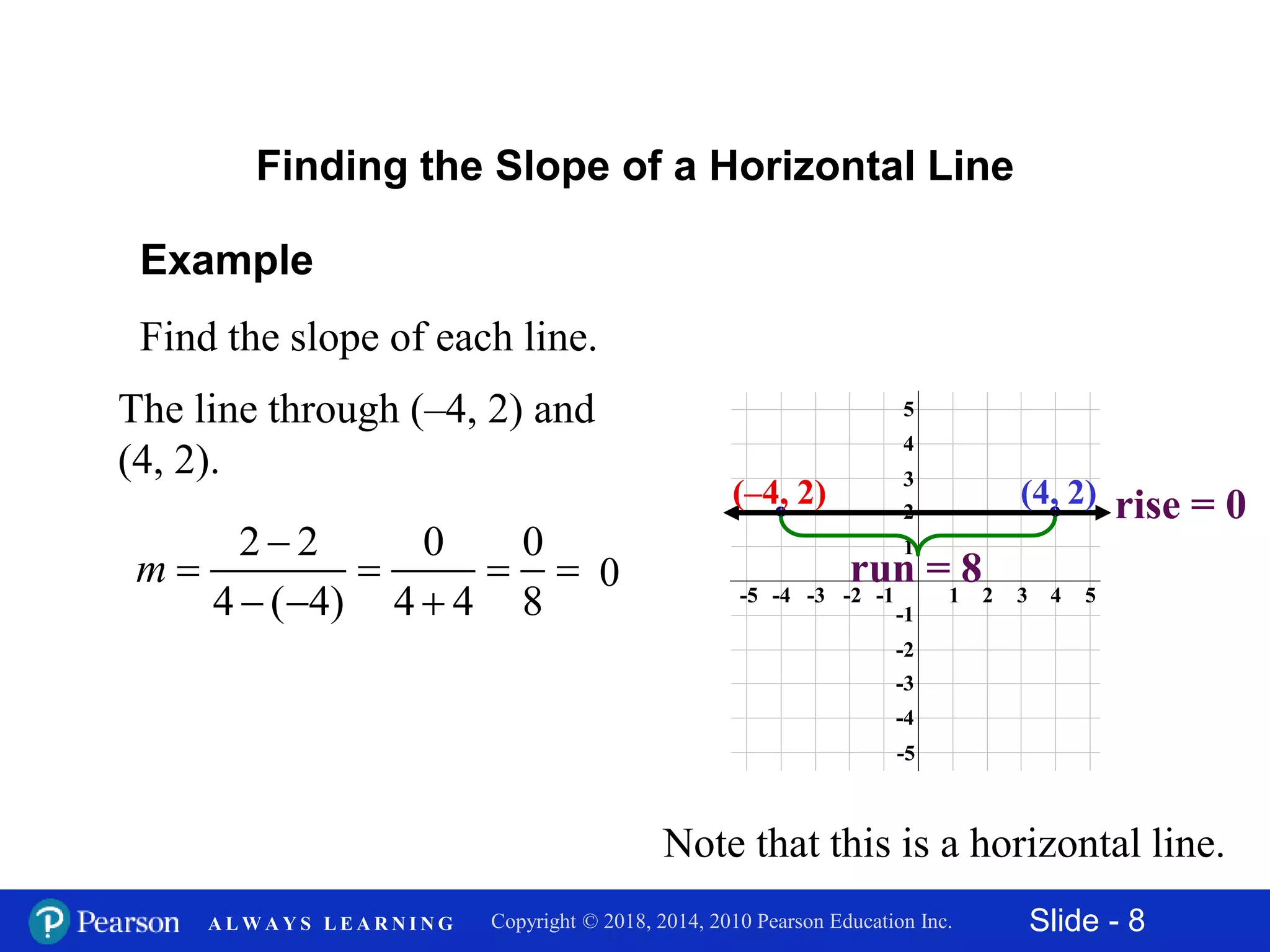
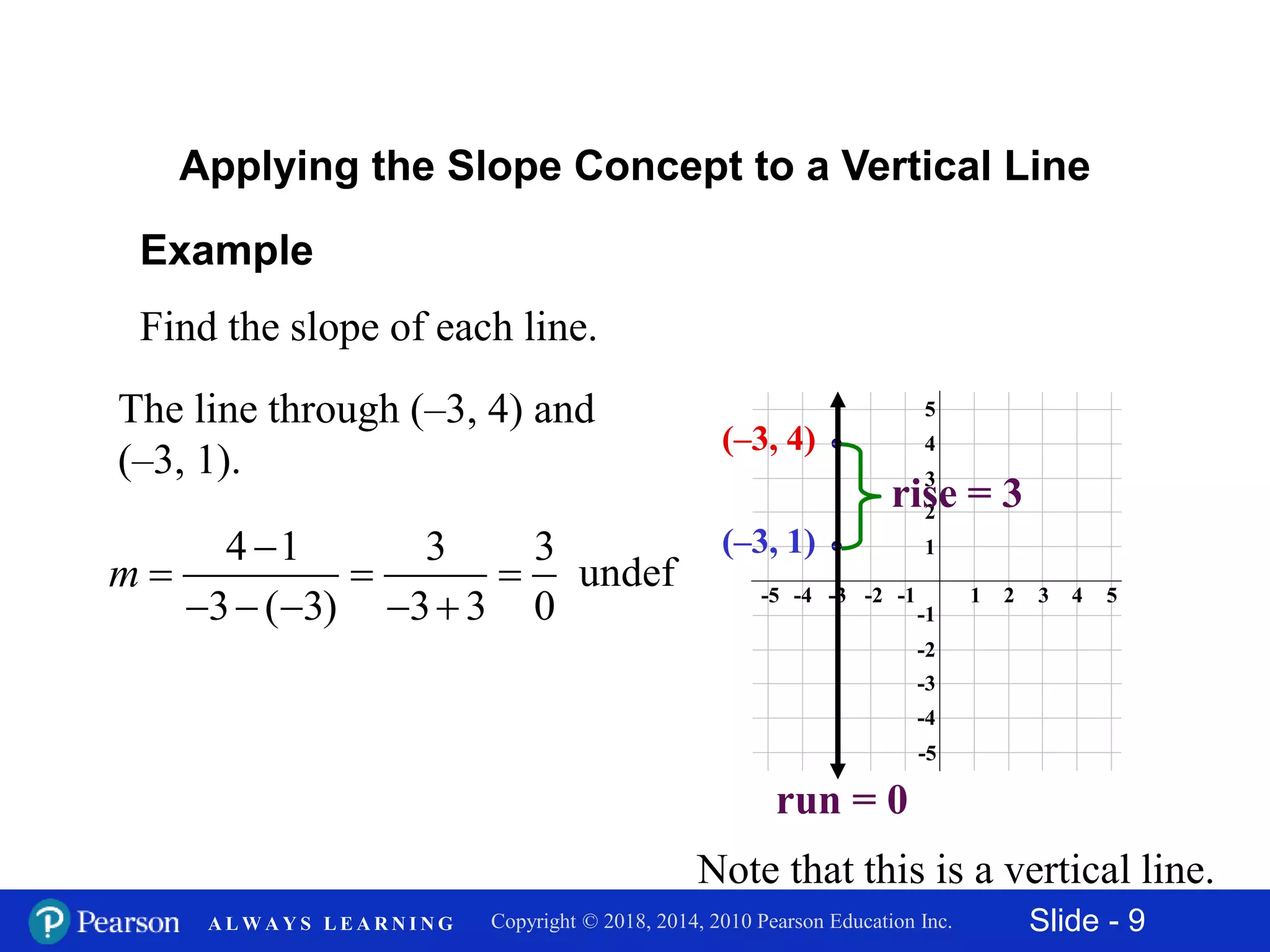
This document discusses finding the slope of a line from two points or an equation. It provides the slope formula and explains how to calculate slope given two points on a line. It also discusses horizontal and vertical lines, which have slopes of 0 and undefined, respectively. The document shows how to find the slope of a line from its equation by solving for y and taking the coefficient of x. It concludes by explaining how to determine if two lines are parallel, perpendicular, or neither based on the equality or product of their slopes. Examples are provided to demonstrate these concepts.