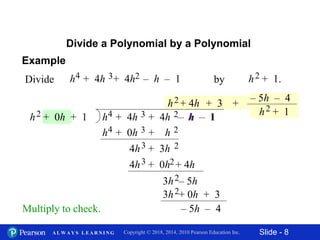
This document contains 11 slides about dividing polynomials by polynomials. It provides examples of dividing polynomials with variables like x, y, h, a by other polynomials. It demonstrates setting up the long division and checking the work by multiplication. One slide applies the division concept to find the length of a rectangle given its area and width as polynomials. The overall document teaches how to divide polynomials and applies it to a geometry problem.

1. Slide - 1Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
2
Exponents and
Polynomials
12

2. Slide - 2Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
1. Divide a polynomial by a polynomial.
2. Apply polynomial division to a geometry
problem.
Objectives
12.8 Dividing a Polynomial by a Polynomial

3. Slide - 3Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
6696
Dividing Whole Numbers
Divide 6696 by 27.
27
2
– 54
129
4
– 108
216
8
0
– 216
Multiply to check. 27 · 248 = 6696
Divide a Polynomial by a Polynomial

4. Slide - 4Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Divide a Polynomial by a Polynomial
(a) Divide 3x + 56x – 2x – 2x + 303 2 by .
3x + 5 6x – 2x – 2x + 303 2
+ 3018x
6x + 10x3 2
2x2
– 12x2 – 2x
– 12x – 20x2
– 4x + 6
18x + 30
0
divided by 3x = – 4x ;– 12x2
6x – 2x – 2x + 303 2
=
.
(2x2 – 4x + 6)(3x + 5)
Example

5. Slide - 5Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Divide a Polynomial by a Polynomial
(b) Divide – 2y + 7– 8y + 30y – 9y + 103 2 by .
– 8y + 30y – 9y + 103 2– 2y + 7
4y 2
– 8y + 28y3 2
2y 2
– 9y
– y
+ 10
+ 1
2y – 7y2
– 2y
– 2y + 7
3
3
– 2y + 7+
Example (cont)

6. Slide - 6Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Divide a Polynomial by a Polynomial
Check.
– 8y + 30y – 9y + 103 2
– 2y + 7
– 8y + 30y – 9y + 103 2
= 4y 2 – y + 1
3
– 2y + 7+
4y 2 – y + 1
3
– 2y + 7+– 2y + 7 =
4y 2– 2y + 7 – y– 2y + 7+
1– 2y + 7
+
3
– 2y + 7– 2y + 7+
= – 8y + 28y3 2 + 2y – 7y2 – 2y + 7 + 3
=
Example (cont)

7. Slide - 7Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Divide a Polynomial by a Polynomial
Divide n – 2.n – 83 by
n – 2 n + 0n + 0n – 83 2
n2
2n – 4n2
n – 2n3 2
2n 2
+ 0n
+ 2n
0
+ 4
– 8
4n
4n – 8
Multiply to check.
(n2 + 2n + 4)(n – 2) n – 83
=
Example

8. Slide - 8Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Divide a Polynomial by a Polynomial
Multiply to check.
Divide h + 1.h + 4h + 4h – h – 14 by3 2 2
h2
h + 4h + 4h – h – 14 3 2h + 0h + 12
h + 0h + h4 3 2
– h – 1
4h + 0h + 4h3 2
+ 4h + 3
4h + 3h3 2
3h – 5h2
3h + 0h + 32
– 5h – 4
– 5h – 4
h + 12
+
Example

9. Slide - 9Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Divide a Polynomial by a Polynomial
Multiply to check.
Divide by 6a + 12.6a + 20a + 13a – 63 2
6a + 12a3 2
6a + 20a + 13a – 63 26a + 12
a2
0
8a + 16a2
8a 2
+ 13a
+ 4
3
a – 1
2
– 3a – 6
– 3a
– 6
Example

10. Slide - 10Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Apply Division to a Geometry Problem
The area of the rectangle in the figure below is given by
sq. units and the width by units.
What is its length?
x + 2x + 4x + 8x + 83 2
x + 2
Area = x + 4 x + 8x + 83 2
Since A = LW, solving for L gives L =
A
W
by the width, x + 2.Divide x + 4x + 8x + 83 2
Example

11. Slide - 11Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Apply Division to a Geometry Problem
The area of the rectangle in the figure below is given by
sq. units and a width by units.
What is its length?
x + 2x + 4x + 8x + 83 2
x + 2 x + 4x + 8x + 83 2
x2
x + 2x3 2
2x 2
+ 8x
+ 2x + 4
2x + 4x2
4x + 8
4x
+ 8
0
The quotient represents the
length of the rectangle.
Example (cont)