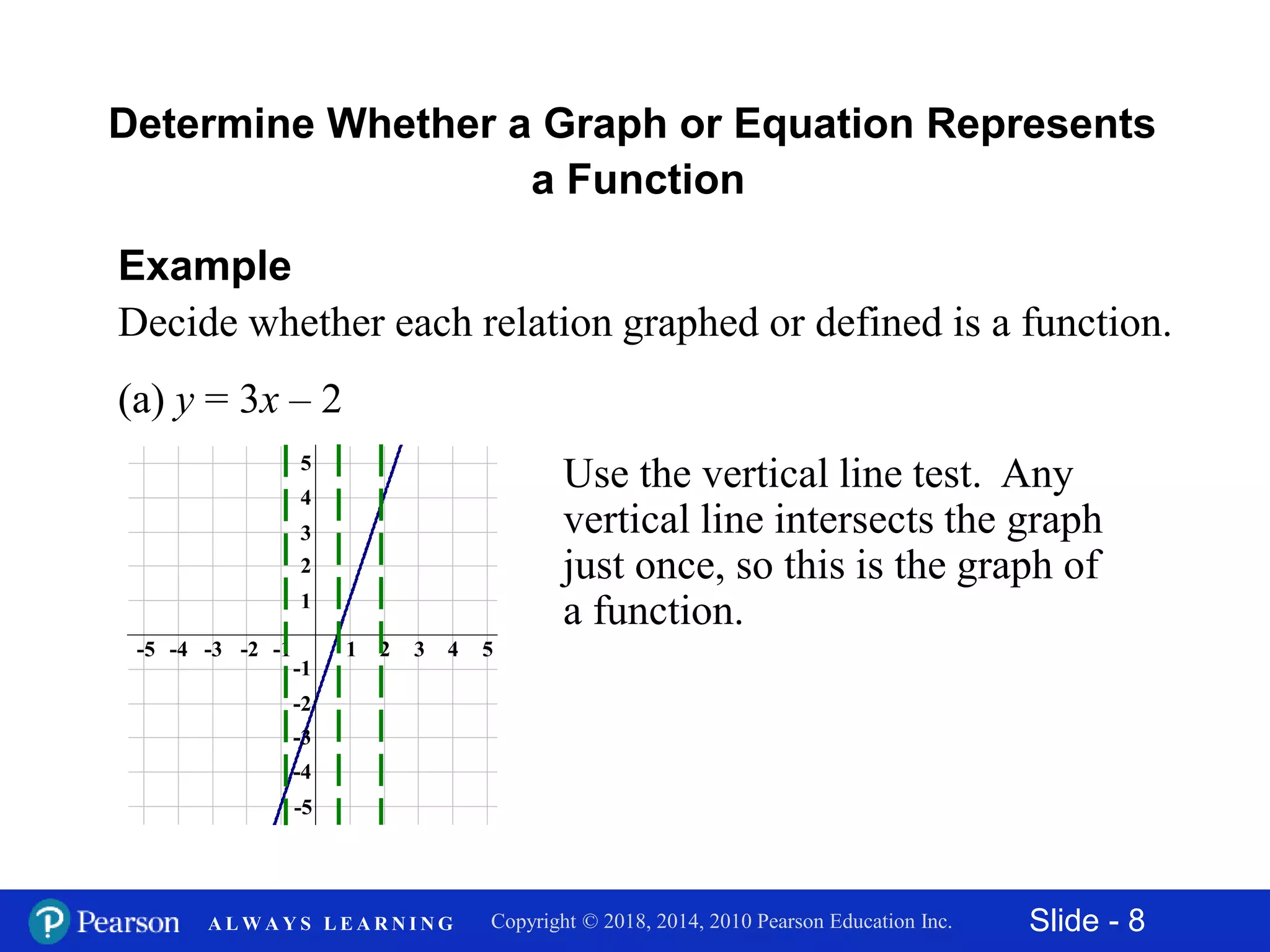
This document discusses functions and how to determine if a relation represents a function. It defines relations and functions, and explains how to identify the domain and range of a relation. It also describes how to use the vertical line test to determine if a graph or equation defines a function. The document demonstrates using function notation to evaluate functions at given x-values and applies the function concept to an example about annual profits of a jeans company.

1. Slide - 1Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
2
Quadratic
Equations
17

2. Slide - 2Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
1. Understand the definition of a relation.
2. Understand the definition of a function.
3. Determine whether a graph or equation
represents a function.
4. Use function notation.
5. Apply the function concept in an application.
Objectives
17.5 Introduction to Functions

3. Slide - 3Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Understand the Definition of a Relation
In an ordered pair (x, y), x and y are called the components
of the ordered pair.
Any set of ordered pairs is called a relation.
The set of all first components in the ordered pairs of a
relation is the domain of the relation, and the set of all
second components in the ordered pairs is the range of
the relation.

4. Slide - 4Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Identify the domain and the range for the relation
{(–2,5), (1,6), (1,3), (3,3), (5,3)}.
Example
Understand the Definition of a Relation
The domain is the set of all first components, and the range is
the set of all second components.
The domain is {–2, 1, 3, 5} and the range is {3, 5, 6}.
The relation is not a function, because the first
component, 1, corresponds to more than one second component.

5. Slide - 5Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Understand the Definition of a Function
Function
A function is a set of ordered pairs (a relation) in which
each distinct first component corresponds to exactly one
second component.

6. Slide - 6Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Example
Determine whether each relation is a function.
Understand the Definition of a Function
(a) {(1,2), (2,2), (3,4), (4,3), (5,6), (6,6)}
This relation IS a function because each number in the domain
corresponds to only one number in the range.
(b) {(1,2), (2,2), (3,4), (4,3), (6,5), (6,6)}
This relation IS NOT a function because 6 in the domain
corresponds to both 5 and 6 in the range.

7. Slide - 7Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Decide Whether an Equation Defines a Function
Vertical Line Test
If a vertical line intersects a graph in more than
one point, the graph is not the graph of a
function.

8. Slide - 8Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Example
Decide whether each relation graphed or defined is a function.
(a) y = 3x – 2
Determine Whether a Graph or Equation Represents
a Function
Use the vertical line test. Any
vertical line intersects the graph
just once, so this is the graph of
a function.
-5
-3
-1
-4
-2
1
3
5
2
4
42-2-4 531-1-3-5

9. Slide - 9Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Example (cont)
Decide whether each relation graphed or defined is a function.
Determine Whether a Graph or Equation Represents
a Function
(b) x2 + y2 = 4
The vertical line test shows that
this is not the graph of a function;
a vertical line could intersect the
graph twice.
-5
-3
-1
-4
-2
1
3
5
2
4
42-2-4 531-1-3-5

10. Slide - 10Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Use Function Notation
The letters f, g, and h are commonly used to name functions.
For example, the function with defining equation y = 3x +5
may be written
f (x) = 3x + 5,
where f (x) is read “ f of x.” The notation f (x) is another way
of writing y in a function.
For the function defined by f (x) = 3x + 5, if x = 7 then
f (7) = 3·7 + 5 = 26.
Read this result, f (7) = 26, as “ f of 7 equals 26.” The notation
f (7) means the value of y when x is 7. The statement f (7) = 26
says that the value of y is 26 when x is 7. It also indicates the
point (7, 26) lies on the graph of f.

11. Slide - 11Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Function Notation
In the notation f(x), remember the following.
f is the name of the function.
x is the domain value.
f(x) is the range value y for the domain value x.
Use Function Notation
CAUTION
The notation f(x) does not mean f times x. It represents
the y-value that corresponds to x in function f.

12. Slide - 12Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Using Function Notation
Example
For the function defined by f (x) = –2x2 + 3x – 1, find the
following.
(a) f (5)
Substitute 5 for x.
f (5) = –2(5)2 + 3(5) – 1
f (5) = –50 + 15 – 1
f (5) = –36
(b) f (0)
f (0) = –2(0)2 + 3(0) – 1
f (0) = – 1
Substitute 0 for x.

13. Slide - 13Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Apply the Function Concept in an Application
The profits for Jeannie’s Jeans is given in the table below.
Example
(a) If we choose years as the domain elements and profits as
the range elements, does this relation represent a function?
Why/why not?
Year 2001 2002 2003 2004 2005 2006
Profit
(in millions)
$0.75 $1.6 $2.1 $3.8 $3.8 $4.7
Yes, this is a function because each year corresponds to exactly
one profit.

14. Slide - 14Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
The profits for Jeannie’s Jeans is given in the table below.
Example (cont)
Year 2001 2002 2003 2004 2005 2006
Profit
(in millions)
$0.75 $1.6 $2.1 $3.8 $3.8 $4.7
Apply the Function Concept in an Application
(b) Find f (2002) and f (2005).
f (2002) = $1.6 million
f (2005) = $3.8 million
(c) For what x value does
f (x) equal $2.1 million?
f (2003) = $2.1 million