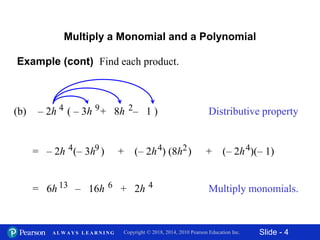
This document discusses different methods for multiplying polynomials, including: 1) Multiplying a monomial and polynomial using the distributive property. 2) Multiplying two polynomials by distributing each term of one polynomial over each term of the other. 3) Multiplying binomials using the FOIL (First, Outer, Inner, Last) method. FOIL involves multiplying the first, outer, inner, and last terms of each binomial. The document provides examples of applying each of these multiplication methods to polynomials with variables like x, y, and n.

1. Slide - 1Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
2
Exponents and
Polynomials
12

2. Slide - 2Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
1. Multiply monomials.
2. Multiply a monomial and a polynomial.
3. Multiply two polynomials.
4. Multiply binomials by the FOIL method.
Objectives
12.5 Multiplying Polynomials

3. Slide - 3Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply a Monomial and a Polynomial
(a) 5x ( 6x + 7 )2 4
Distributive property= 5x ( 6x )2 4 + 5x ( 7 )2
= 30x + 35x6 2 Multiply monomials.
Example Find each product.

4. Slide - 4Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply a Monomial and a Polynomial
Distributive property
= – 2h (– 3h )4 9
(b) – 2h ( – 3h + 8h – 1 )4 9 2
+ (– 2h ) (8h )4 2 + (– 2h )(– 1)4
Example (cont) Find each product.
Multiply monomials.= 6h 13 – 16h 6 + 2h 4

5. Slide - 5Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Two Polynomials
Multiplying Polynomials
To multiply two polynomials, multiply each term of the
second polynomial by each term of the first polynomial
and add the products.

6. Slide - 6Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Two Polynomials
Distributive property( 2y – 5 ) ( 2y – 7y + 4 )2 3
= (2y )2 (2y )3 (–7y)(2y )2+ (4)(2y )2+
(–7y)+ (–5) (4)+ (–5)(–5)(2y )3+
= 4y 5 14y 3– 8y 2+ – 20+ 35y– 10y 3
= 4y 5 24y 3– 8y 2+ + 35y – 20 Combine like terms.
  2 3
Multiply 2 5 2 7 4 .y y y  Example

7. Slide - 7Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
5n + 8n – 3n – 23 2
Multiply Two Polynomials
4n + 32
– 6– 9n+ 24n 215n 3
– 8n 2– 12n 3+ 32n 420n 5
– 6– 9n+ 3n 3+ 32n 420n 5 + 16n 2
  2 3 2
Multiply 4 3 5 8 3 2 vertically.n n n n   Example

8. Slide - 8Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Binomials by the FOIL Method
Multiplying Binomials by the FOIL Method
Step 1 Multiply the two First terms of the binomials to
get the first term of the answer.
Step 2 Find the Outer product and the Inner product
and add them (when possible) to get the
middle term of the answer.
Step 3 Multiply the two Last terms of the binomials to
get the last term of the answer.

9. Slide - 9Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Binomials by the FOIL Method
F
( y – 4 ) ( 3y – 2 )
O
I
L
y ( 3y )
y ( – 2 )
– 4 ( 3y )
– 4 (– 2 )
= 3y – 2y – 12y + 82
= 3y – 14y + 82
F O I L
Example   Use the FOIL method to find 4 3 2 .y y 
Multiply the last terms:
Multiply the inner terms:
Multiply the outer terms:
Multiply the first terms:

10. Slide - 10Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Binomials by the FOIL Method
F
( n – 7 ) ( 5n + 1 )
O
I
L
n ( 5n )Multiply the first terms:
n ( 1 )Multiply the outer terms:
– 7 ( 5n )Multiply the inner terms:
– 7 ( 1 )Multiply the last terms:
= 5n + n – 35n – 72
= 5n – 34n – 72
F O I L
Example   Multipy 7 5 1 .n n 

11. Slide - 11Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Binomials by the FOIL Method
F
( 3g + 2 ) ( 9g – 4 )
O
I
L
3g ( 9g )Multiply the first terms:
3g ( – 4 )Multiply the outer terms:
2 ( 9g )Multiply the inner terms:
2 ( – 4 )Multiply the last terms:
= 27g – 12g + 18g – 82
= 27g + 6g – 82
F O I L
Example   Find the product 3 2 9 4 . g g

12. Slide - 12Copyright © 2018, 2014, 2010 Pearson Education Inc.A L W A Y S L E A R N I N G
Multiply Binomials by the FOIL Method
F
( 6a + 3b ) ( 4a – 2b )
O
I
L
6a ( 4a )Multiply the first terms:
6a ( – 2b )Multiply the outer terms:
3b ( 4a )Multiply the inner terms:
3b ( – 2b )Multiply the last terms:
F O I L
= 24a – 12ab + 12ab – 6b2 2
= 24a – 6b2 2
Example   Find the product 6 3 4 2 .a b a b 