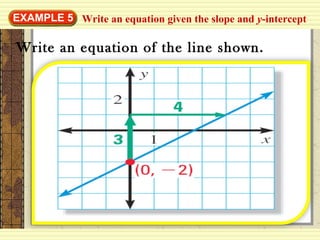
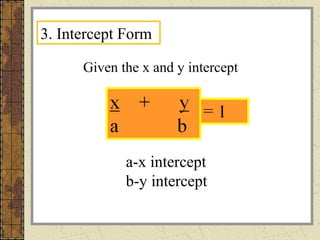
1. The document discusses various forms of linear equations including general, two-point, intercept, point-slope, and slope-intercept forms. 2. It provides examples of writing equations in each form given specific information like two points, an x-intercept and y-intercept, a point and slope, or just a slope and y-intercept. 3. Guided practice problems are included for writing equations parallel or perpendicular to a given line.

2. Various Forms of an Equation
of a Line.
1. General Form
Ax + By + C = 0
2. Two point Form
Given two points

3. 3. Intercept Form
Given the x and y intercept
a-x intercept
b-y intercept

4. 4. Point Slope Form
y - y1 = m (x-x1)
Given a point and slope (m)
5. Slope Intercept Form
Given the slope (m) and y-intercept (b)
y = mx + b

5. 1. Passing trough (-1, -3) and (2, -1)
Write an equation given two pointsEXAMPLE 1
-1 - (-3)
2 – (-1)
(x – (-1))y – (-3) =

6. -1+ 3
2 + 1
(x + 2)y + 3 =
3y + 9 = 2x + 2
0 = 2x – 3y – 9 + 2
0 = 2x – 3y – 7 = 0
2x – 3y – 7 = 0
General form
Two points form

7. Write an equation given a point and slope (m).EXAMPLE 2
y - y1 = m (x-x1)
1. Passing trough (2, -1) with a slope of ?
y – (-1) = 2/3 (x-2)
y +1 = 2/3 (x-2)
Point slope form

8. 3y + 3 = 2x - 4
0 = 2x – 3y – 3 - 4
0 = 2x – 3y – 7
2x – 3y – 7 = 0
3(y + 1) = 2 (x- 2)
General form

9. Write an equation given the x and y intercept.EXAMPLE 3
1. Passing x intercept of 3 and y- intercept of ?
x + y
a b
= 1
[ ] 12 LCD
x + y
3 4
= 1

10. [ ] 12 LCD
x + y
3 4
= 1
4x + 3y = 12
4x + 3y – 12 = 0
General form
Intercept Form

11. Write an equation given the slope (m) and
y-intercept (b)EXAMPLE 4
y = mx + b
1. Having slope of 2/3 and y – intercept of ?
2 + -7
3 3
y =

12. 2 + -7
3 3
y =LCD 3 [ ]
General form
3y = 2x – 7
0 = 2x – 3y – 7
= 2x – 3y – 7 = 0
Slope intercept form

13. Write an equation given the slope and y-interceptEXAMPLE 5
Write an equation of the line shown.

14. GUIDED PRACTICE for Example 5
Write an equation of the line that has
the given slope and y-intercept.
1. m = 3, b = 1
y = x + 13
ANSWER
2. m = –2 , b = –4
y = –2x – 4
ANSWER
3. m = – , b =3
4
7
2
y = – x +3
4
7
2
ANSWER

15. SOLUTION
Write an equation given the slope and y-interceptEXAMPLE 6
From the graph, you can see that the slope
is m = and the y-intercept is b = –2.
Use slope-intercept form to write an
equation of the line.
3
4
y = mx + b Use slope-intercept form.
y = x + (–2)
3
4
Substitute for m and –2 for b
.
3
4
y = x (–2)3
4
Simplify.

16. Write an equation given the slope and a pointEXAMPLE 7
Write an equation of the line that
passes through (5, 4) and has a slope of
–3.
Because you know the slope and a point on
the line, use point-slope form to write an
equation of the line. Let (x1, y1) = (5, 4) and
m = –3.y – y1 = m(x – x1) Use point-slope form.
y – 4 = –3(x – 5) Substitute for m, x1, and y1.
y – 4 = –3x + 15 Distributive property
SOLUTION
y = –3x + 19 Write in slope-intercept form.

17. EXAMPLE 8
Write an equation of the line that passes
through (–2,3) and is (a) parallel to, and (b)
perpendicular to, the line y = –4x + 1.
SOLUTION
a. The given line has a slope of m1 = –4.
So, a line parallel to it has a slope of m2
= m1 = –4. You know the slope and a
point on the line, so use the point-slope
form with (x1, y1) = (–2, 3) to write an
equation of the line.
Write equations of parallel or perpendicular lines

18. EXAMPLE 8
y – 3 = –4(x – (–2))
y – y1 = m2(x – x1) Use point-slope form.
Substitute for m2, x1, and y1.
y – 3 = –4(x + 2) Simplify.
y – 3 = –4x – 8 Distributive property
y = –4x – 5 Write in slope-intercept form.
Write equations of parallel or perpendicular lines

19. EXAMPLE 8
b. A line perpendicular to a line with slope m1 = –4 has
a slope of m2 = – = . Use point-slope form with
(x1, y1) = (–2, 3)
1
4
1
m1
y – y1 = m2(x – x1) Use point-slope form.
y – 3 = (x – (–2))
1
4
Substitute for m2, x1, and y1.
y – 3 = (x +2)
1
4
Simplify.
y – 3 = x +
1
4
1
2
Distributive property
Write in slope-intercept form.
Write equations of parallel or perpendicular lines
y = x +1
4
7
2

20. GUIDED PRACTICEGUIDED PRACTICE
Write an equation of the line that passes
through (–1, 6) and has a slope of 4.
y = 4x + 10
Write an equation of the line that passes
through (4, –2) and is (a) parallel to, and (b)
perpendicular to, the line y = 3x – 1.
y = 3x – 14ANSWER
ANSWER

21. Write an equation given two pointsEXAMPLE 10
Write an equation of the line that passes
through (5, –2) and (2, 10).
SOLUTION
The line passes through (x1, y1) = (5,–2) and
(x2, y2) = (2, 10). Find its slope.
m =
y2 – x2

22. Write an equation given two pointsEXAMPLE 10
You know the slope and a point on the
line, so use point-slope form with either
given point to write an equation of the
line. Choose (x1, y1) = (4, – 7).
y2 – y1 = m(x – x1) Use point-slope form.
y – 10 = – 4(x – 2) Substitute for m, x1, and y1.
y – 10 = – 4x + 8 Distributive property
Write in slope-intercept form.y = – 4x + 8