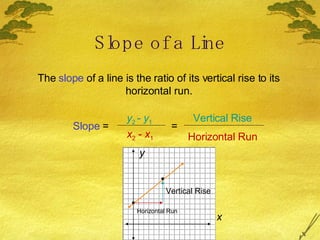
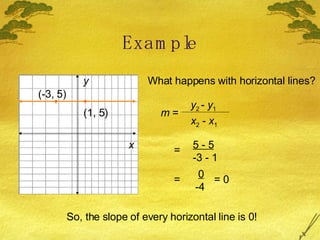
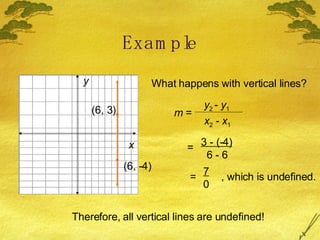
This document discusses slopes of lines and their uses in transportation. It provides formulas and examples for calculating slopes from two points on a line. Key points made include: 1) The slope of a line is the ratio of its vertical rise to its horizontal run and indicates whether a line rises, falls, or is horizontal. 2) Parallel lines have the same slope, while perpendicular lines have slopes that multiply to -1. 3) Slope can be used to identify the rate of change in various contexts like increasing sales over time.

1. WARM UP Solve for y: 2 x + 4 y = -5 HAVE HOMEWORK OUT READY TO BE CHECKED: Pg. 136; # 1, 3, 5 - 9 odd, 11, 13, 15, 21, 29, 38, 45, 46. Discuss Tests!

2. Slopes of Lines 3.3

3. Objectives Find the slopes of lines. Use slope to identify parallel and perpendicular lines.

4. HOW is slope used in transportation?

5. Traffic signs are used to alert drivers to road conditions. The sign at the right indicates, a hill with a 6% grade . This means that the road will rise or fall 6 feet vertically for every 100 horizontal feet traveled.

6. HOW is slope used in transportation? Why would a road or train track wind its way up a mountain instead of going directly toward the top? A path going directly toward the top might be too steep for a car or train. To reach the same height, is it easier to push a wheelchair up a long ramp or a short ramp? A long ramp is easier because the climb is less steep, even though you travel father.

7. Slope of a Line The slope of a line is the ratio of its vertical rise to its horizontal run. Slope = y 2 - y 1 x 2 - x 1 = Vertical Rise Horizontal Run x y Horizontal Run Vertical Rise

8. Slope The slope m of a line containing two points with coordinates ( x 1 , y 1 ) and ( x 2 , y 2 ) is given by the formula: m = y 2 - y 1 x 2 - x 1 , where x 1 = x 2

9. Slope The slope of a line indicates whether the line rises to the right, falls to the right, or is horizontal. The slope of a vertical line, where x 1 = x 2 , is undefined.

10. Find the slope of a line… From (-3, -2) to (-1, 2), Go up four units and right 2 units. Use the slope formula. Let (-4, 0) be ( x 1 , y 1 ) and (0, -1) be ( x 2 , y 2 ). Slope = y 2 - y 1 x 2 - x 1 = -1 - 0 0 - (-4) = -1/4 x y ( -1 , 2 ) ( -3 , -2 ) Use the method. rise run rise run = 4 2 = 2 m = ( -4 , 0 ) ( 0 , -1 )

11. Study Tip! Lines with positive slope rise as we move from left to right, while lines with negative slope fall as we move from left to right.

12. Example (-3, 5) (1, 5) What happens with horizontal lines? = 5 - 5 -3 - 1 0 -4 = = 0 So, the slope of every horizontal line is 0! x y m = y 2 - y 1 x 2 - x 1

13. Example (6, 3) (6, -4) What happens with vertical lines? = 3 - (-4) 6 - 6 = 7 0 , which is undefined. Therefore, all vertical lines are undefined! x y m = y 2 - y 1 x 2 - x 1

14. HOMEWORK Pg. 142; #1 - 9, Pg. 144; #51 - 61 odd

15. WARM UP If we want to get a hint about the positivity or negativity of a slope, what can we look for? HW CHECK: Pg. 142; #1 - 9, 51 - 61 odd

16. Rate of Change The slope of a line can be used to identify the coordinates of any point on the line. The rate of change describes how a quantity is changing over time.

17. Use Rate of Change to Solve a Problem Between 1990 and 2000, the annual sales of rollerblade equipment increased by an average rate of $92.4 million per year. In 2000, the total sales were $1074.4 million. If sales increase at the same rate, what will the total be in 2008? Let ( x 1 , y 1 ) = (2000, 1074.4) and m = 92.4 m = y 2 - y 1 x 2 - x 1 Slope formula 92.4 = y 2 - 1074.4 2008 - 2000 Substitution 92.4 = y 2 - 1074.4 8 Simplify 739.2 = y 2 - 1074.4 Multiply by 8 on each side! 1813.6 = y 2 <- Answer!

18. Therefore, The coordinates of the point representing the sales for 2008 are (2008, 1813.6). Thus, the total sales in 2008 will be about $1813.6 million.

19. Parallel and Perpendicular Lines Examine the graphs of lines l , m , and n . Lines l and m are parallel, and n is perpendicular to l and m . Let’s investigate! (-3, 5) (2, 2) (1, -3) (0, 4) (4, 2) l m n Slope of line l ? Slope of line m ? Slope of line n ? Because lines l and m are parallel, their slopes are the same. Line n is perpendicular to line l and m , and its slope is the opposite reciprocal of the slopes of l and m . x y m = - 3 5 m = - 3 5 m = 5 3

20. Slopes of Parallel and Perpendicular Lines Postulate 3.2 - Two nonvertical lines have the same slope if and only if they are parallel. Postulate 3.3 - Two nonvertical lines are perpendicular if and only if the product of their slopes is -1.

22. My Name is Ned the Ninja! I will be helping you throughout Chapter 3!

23. HOMEWORK Pg. 142; #15 - 41 odd.