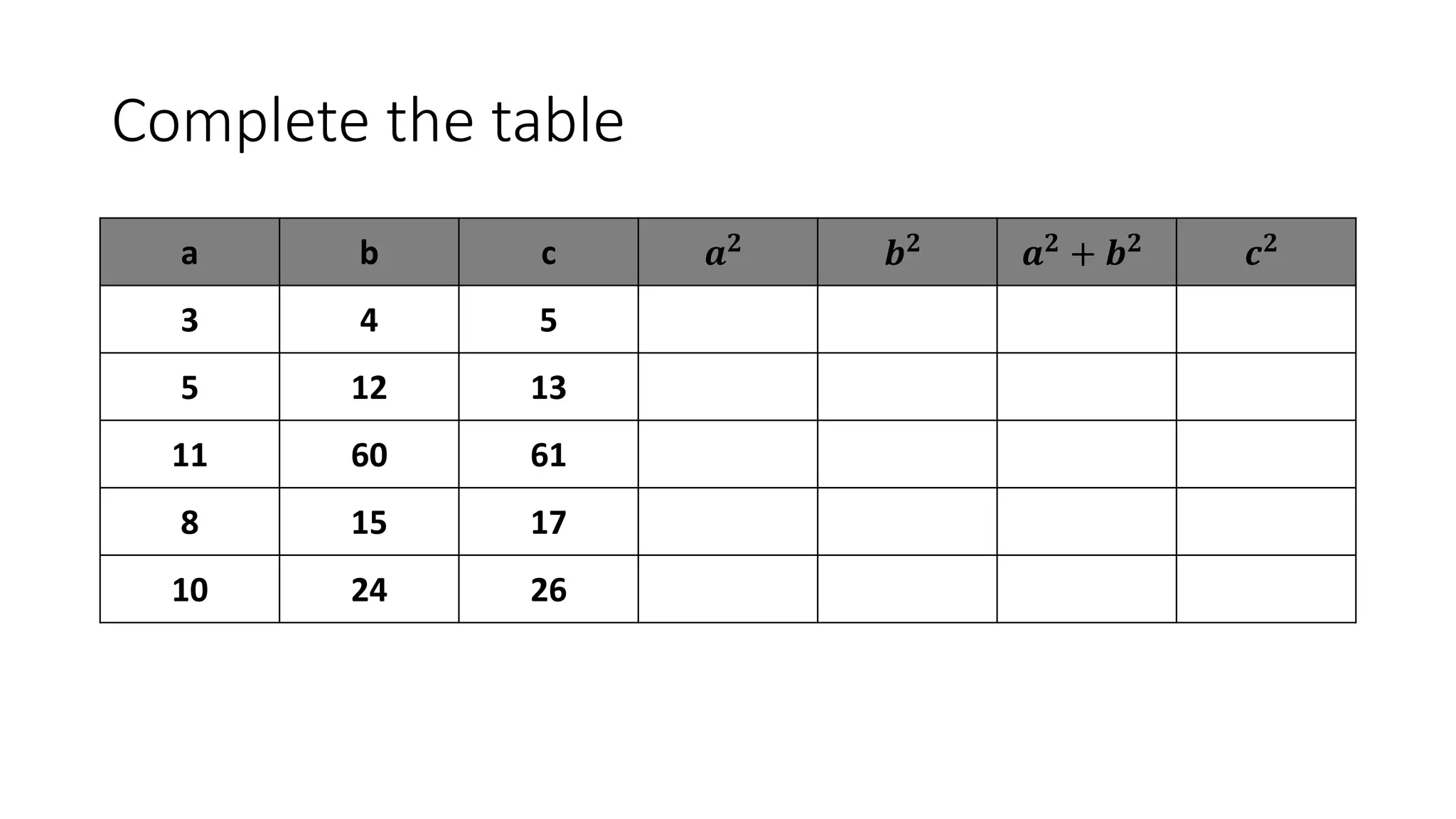
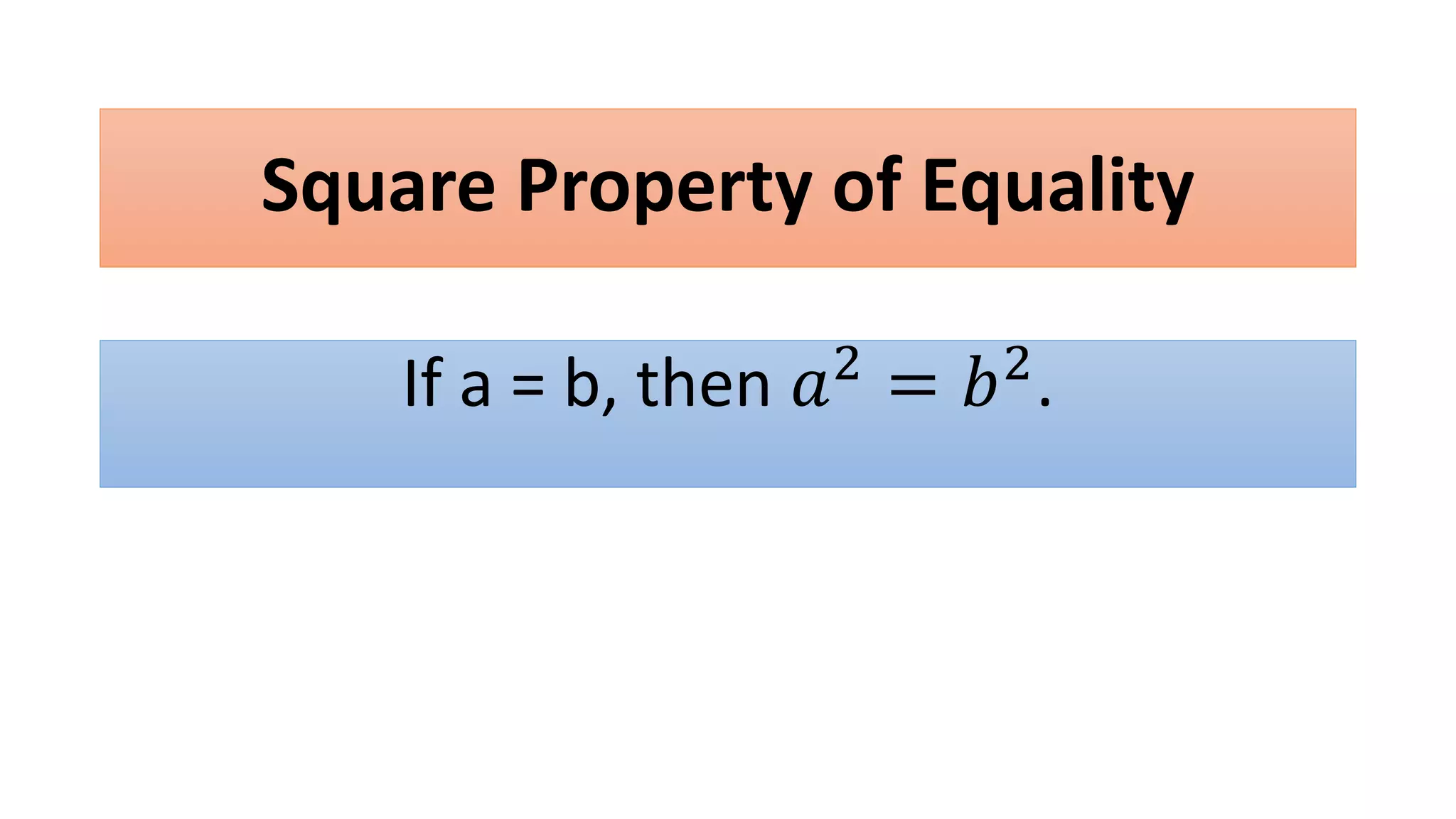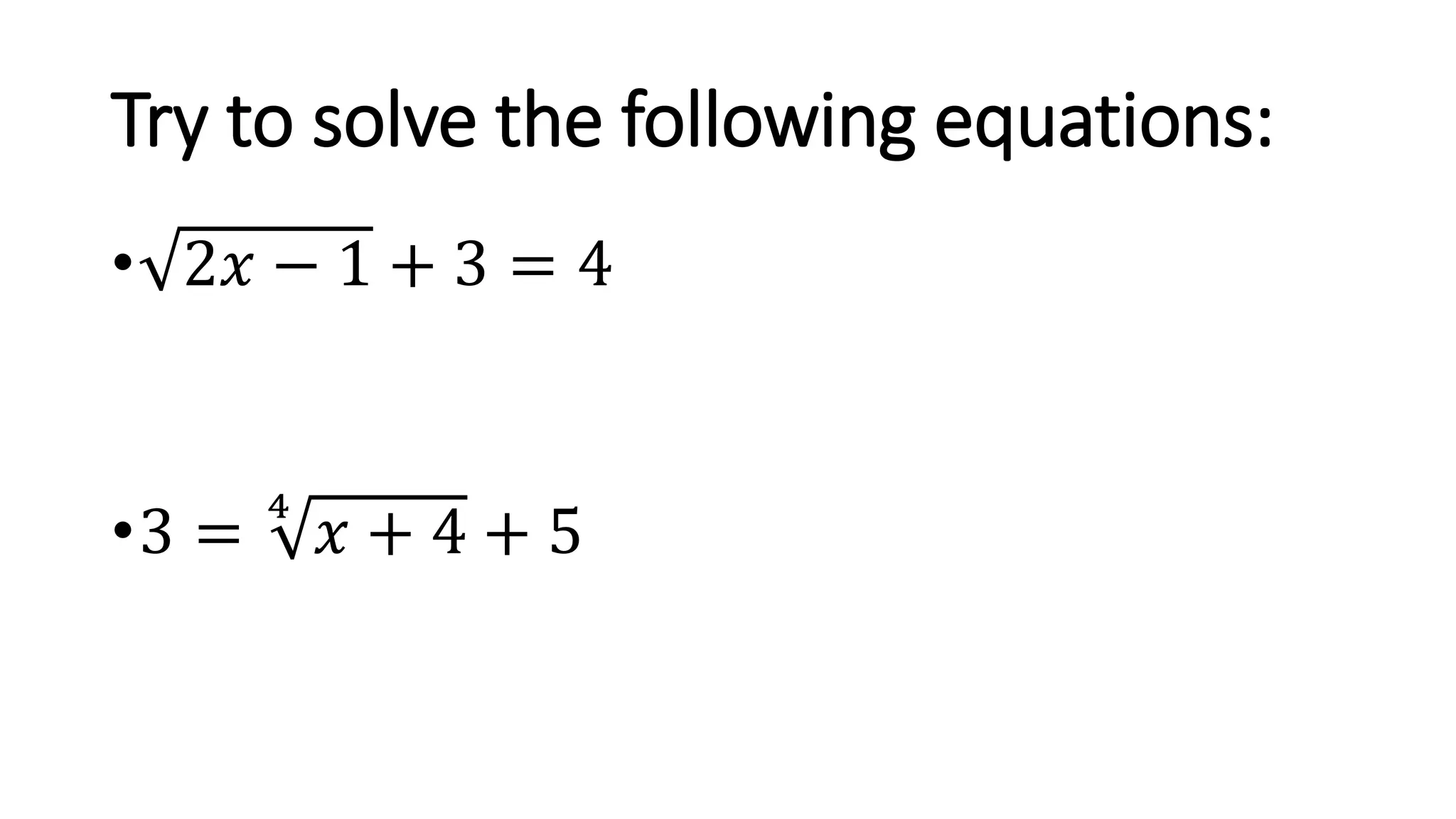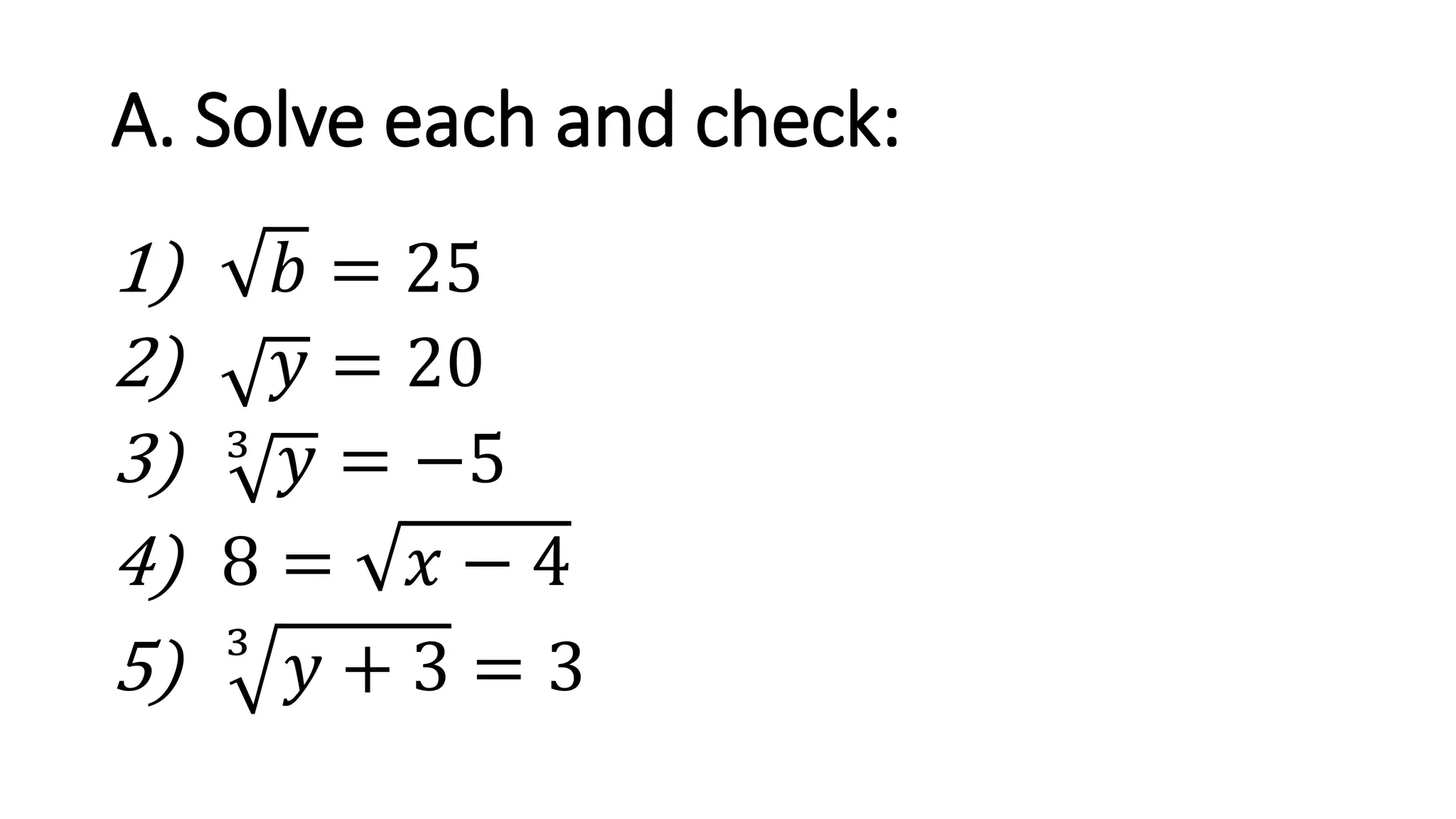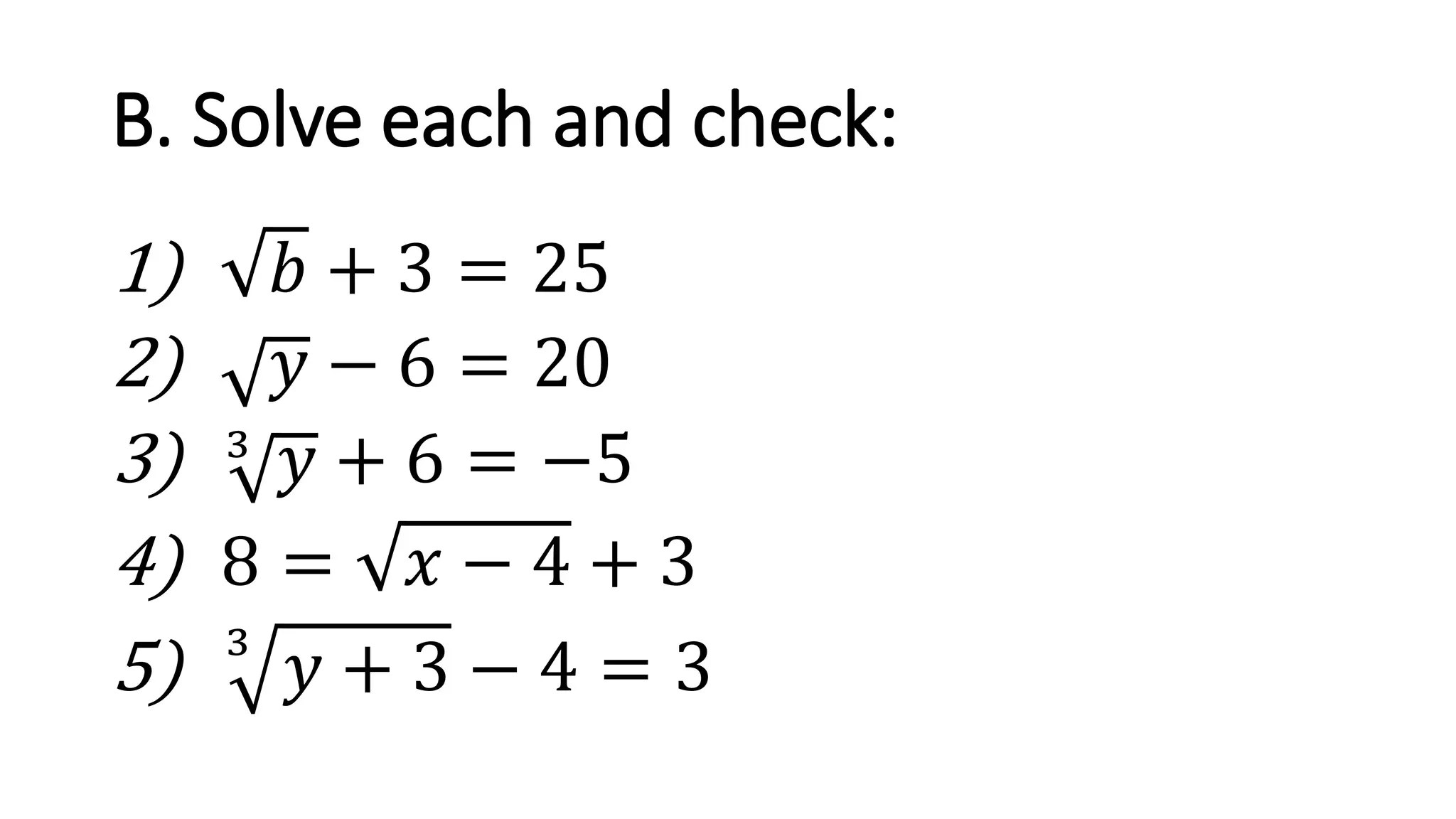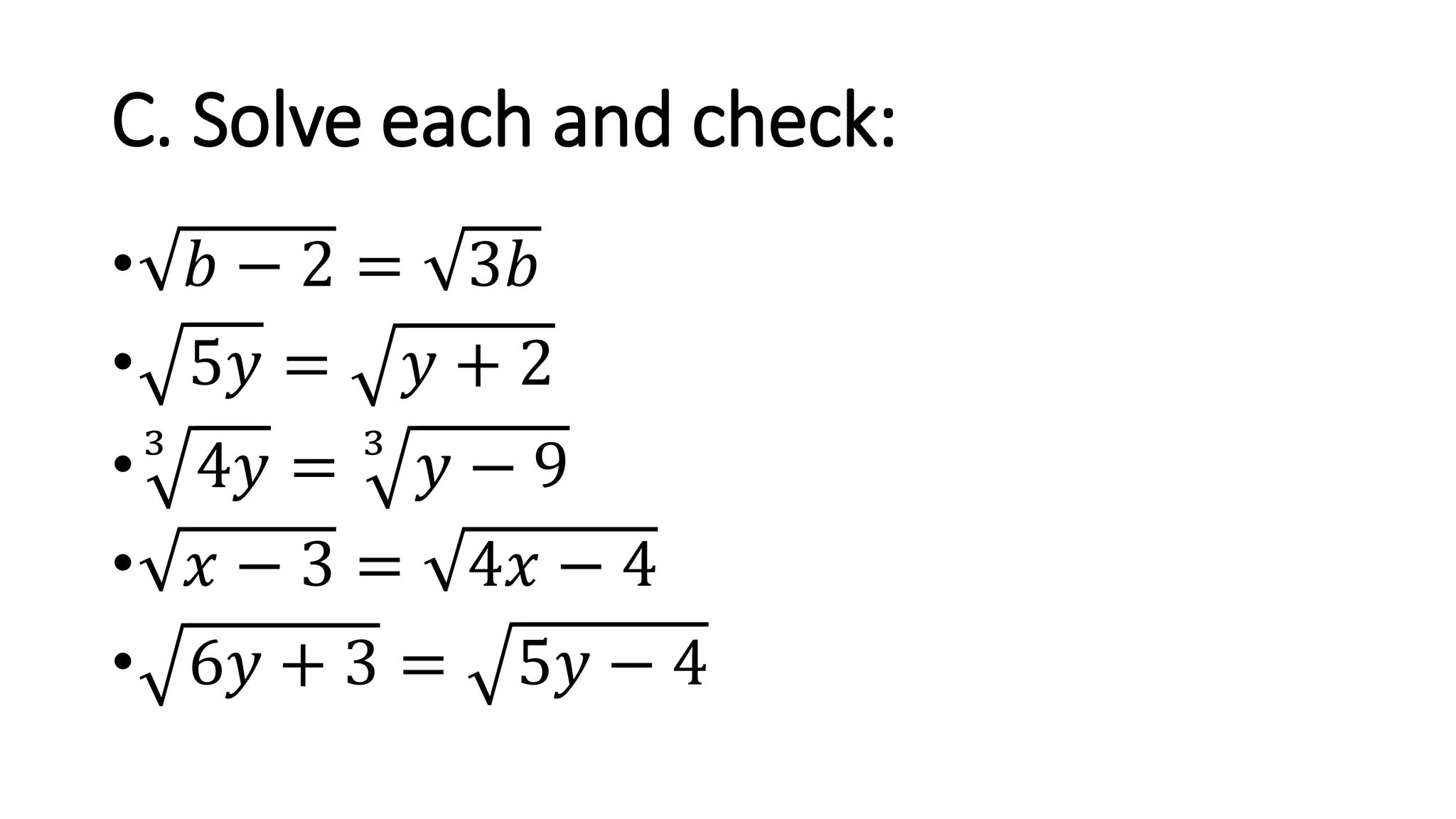The document discusses solving radical equations. It introduces radical equations and explains that to solve them, one isolates the radical term, raises both sides of the equation to the equivalent index to eliminate the radical, solves the resulting equation, and checks the solution. It provides examples of solving various radical equations and checking the solutions. It also discusses using the Pythagorean theorem and solving problems involving areas of squares and lengths of sides and diagonals.

1. Solving Radical
Equations

2. In this chapter, you will learn to:
•Solve equations involving radical expressions
•Solve problems involving radicals

3. Complete the table
a b c 𝒂 𝟐
𝒃 𝟐
𝒂 𝟐
+ 𝒃 𝟐
𝒄 𝟐
3 4 5
5 12 13
11 60 61
8 15 17
10 24 26

4. Square Property of Equality
If a = b, then 𝑎2 = 𝑏2.

5. Radical Equation
An equation containing at least one radical expression
whose radicand has a variable is called radical equation
Examples:
1) 3
𝑥 = 4
2) 2
𝑥 + 2 = 6
3) 𝑥 − 1
1
3 − 3 = 1

6. The basis for solving a radical equation is to
eliminate the radical by raising both sides of the
equation to a power equal to the index of the radical.
• 3
𝑥 = 4
• 𝑥 = 7
•
4
𝑥 + 1 = 3

7. Solving Radical Equations
To solve a radical equation, follow
the steps below:
• Isolate the radical term.
• Raise both sides of the equation
to the equivalent index.
• If all the radicals have been
eliminated, then solve.
• Check the solution.
Example: 𝑥 − 8 = 0

8. Solving Radical Equations
To solve a radical equation, follow
the steps below:
• Isolate the radical term.
• Raise both sides of the equation
to the equivalent index.
• If all the radicals have been
eliminated, then solve.
• Check the solution.
Example: 𝑥 + 1 = 5

9. Solving Radical Equations
To solve a radical equation, follow
the steps below:
• Isolate the radical term.
• Raise both sides of the equation
to the equivalent index.
• If all the radicals have been
eliminated, then solve.
• Check the solution.
Example: 𝑥 − 1 − 3 = 1

10. Solving Radical Equations
To solve a radical equation, follow
the steps below:
• Isolate the radical term.
• Raise both sides of the equation
to the equivalent index.
• If all the radicals have been
eliminated, then solve.
• Check the solution.
Example:
3
𝑥 − 1 − 3 = 1

11. Solving Radical Equations
To solve a radical equation, follow
the steps below:
• Isolate the radical term.
• Raise both sides of the equation
to the equivalent index.
• If all the radicals have been
eliminated, then solve.
• Check the solution.
Example: 3𝑥 + 4 = 𝑥 − 2

12. Try to solve the following equations:
• 2𝑥 − 1 + 3 = 4
•3 =
4
𝑥 + 4 + 5

13. Solve each and check:
• 6𝑥 = 18
• 𝑏 = 35
• 𝑦 = 15
•4 = 2𝑥
• 𝑥 + 1 = 7

14. To be continue…

15. A. Solve each and check:
1) 𝑏 = 25
2) 𝑦 = 20
3) 3
𝑦 = −5
4) 8 = 𝑥 − 4
5) 3
𝑦 + 3 = 3

16. B. Solve each and check:
1) 𝑏 + 3 = 25
2) 𝑦 − 6 = 20
3) 3
𝑦 + 6 = −5
4) 8 = 𝑥 − 4 + 3
5) 3
𝑦 + 3 − 4 = 3

17. C. Solve each and check:
• 𝑏 − 2 = 3𝑏
• 5𝑦 = 𝑦 + 2
•3
4𝑦 = 3
𝑦 − 9
• 𝑥 − 3 = 4𝑥 − 4
• 6𝑦 + 3 = 5𝑦 − 4

18. To be continue…

19. Application
The Pythagorean Theorem provides a formula relating the
lengths of the three sides of a right triangle.
The Pythagorean Theorem
If the length of the hypotenuse of a right triangle is c and the lengths of
the two legs are a and b, then
𝒄 𝟐 = 𝒂 𝟐 + 𝒃 𝟐

20. Example:
The legs of a right triangle are congruent and the
hypotenuse is 5 2 units long. Find the length of each leg.
Solution:

21. Example:
The legs of a right triangle are congruent and the
hypotenuse is 7 3 units long. Find the length of each leg.
Solution:

22. Example:
The sides of a square are each 7 feet long. Find the length
of the diagonal.
Solution:

23. Example:
The sides of a square are each 11 feet long. Find the
length of the diagonal.
Solution:

24. Solve each problem:
• The legs of a right triangle are congruent and the hypotenuse
is 4 5 units long. Find the length of each leg.
• The legs of a right triangle are congruent and the hypotenuse
is 9 3 units long. Find the length of each leg.
• The sides of a square are each 10 meters long. Find the
length of the diagonal.
• The sides of a square are each 15 cm long. Find the length of
the diagonal.

25. To be continue…
Solving Problems
involving Radical
Equations

26. Example:
Find the length of the side of a square whose area is 64
square centimeters.
Solution:

27. Example:
Find the length of the side of a square whose area is 50
square centimeters.
Solution:

28. Example:
Find the length of the side of a square garden whose area
is 180 square meters.
Solution:

29. Example:
Find the length of the side of a square whose diagonal is
25 centimeters.
Solution:

30. Example:
Find the length of the side of a square whose diagonal is
18 centimeters.
Solution: