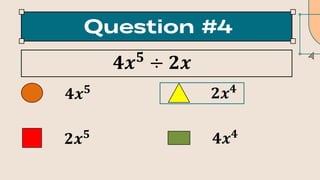
The document covers various operations on functions, including defining and solving piecewise functions and performing arithmetic operations like addition, subtraction, multiplication, and division of functions. Additionally, it illustrates function composition and provides examples related to calculating monthly bills for a cable service based on pay-per-view hours. The document also includes step-by-step solutions for different function scenarios and applications.