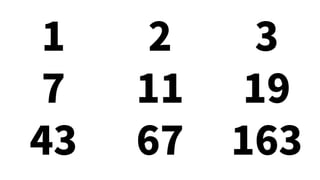
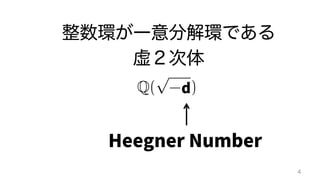
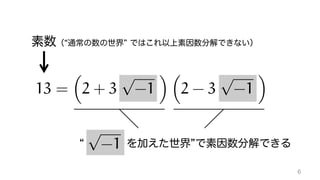
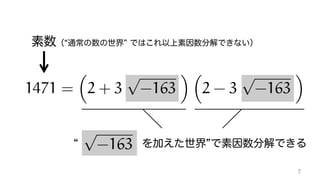
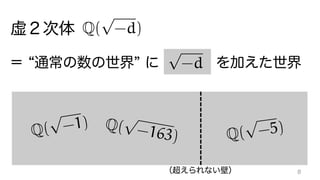
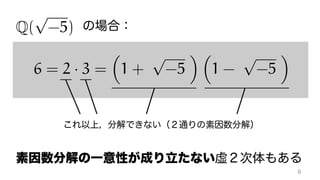
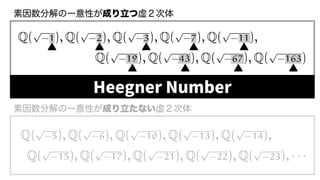
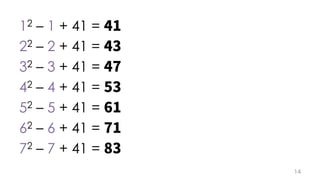
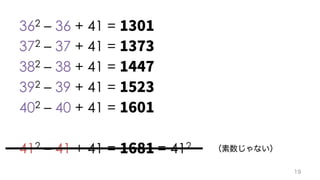
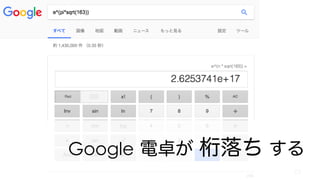
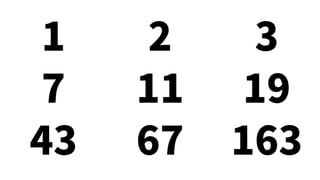
The document contains mathematical equations and discussions involving prime numbers, polynomials, and Heegner numbers. It explores properties of prime-generating polynomials and uses formulas to calculate values of eπ√d for different values of d, relating these to class numbers of imaginary quadratic fields. Bounds on Heegner numbers d are derived based on results from Heilbronn and Linfoot.

1. @tsujimotter
2017/04/01 #

4. Q(
p
-d)

6. p
-1
13 =
⇣
2 + 3
p
-1
⌘ ⇣
2 - 3
p
-1
⌘
13 =
⇣
2 + 3
p
-1
⌘ ⇣
2 - 3
p
-1
⌘

7. 1471 =
⇣
2 + 3
p
-163
⌘ ⇣
2 - 3
p
-163
⌘
p
-163

8. Q(
p
-d)
p
-d
Q(
p
-1) Q(
p
-163) Q(
p
-5)

9. 6 = 2 · 3 =
⇣
1 +
p
-5
⌘ ⇣
1 -
p
-5
⌘
Q(
p
-5)

10. Q(
p
-5), Q(
p
-6), Q(
p
-10), Q(
p
-13), Q(
p
-14), Q(
p
-15)
Q(
p
-15), Q(
p
-17), Q(
p
-21), Q(
p
-22), Q(
p
-23), · · ·
Q(
p
-1), Q(
p
-2), Q(
p
-3), Q(
p
-7), Q(
p
-11), Q(
p
-19), Q
Q(
p
-7), Q(
p
-11), Q(
p
-19), Q(
p
-43), Q(
p
-67), Q(
p
-163)

12. d = -1, -2, -3, -7, -11, -19, -43, -67, -163

13. X2
- X + 41
4 1

14. 12 – 1 + 41 =
22 – 2 + 41 =
32 – 3 + 41 =
42 – 4 + 41 =
52 – 5 + 41 =
62 – 6 + 41 =
72 – 7 + 41 =

15. 82 – 8 + 41 =
92 – 9 + 41 =
102 – 10 + 41 =
112 – 11 + 41 =
122 – 12 + 41 =
132 – 13 + 41 =
142 – 14 + 41 =

16. 152 – 15 + 41 =
162 – 16 + 41 =
172 – 17 + 41 =
182 – 18 + 41 =
192 – 19 + 41 =
202 – 20 + 41 =
212 – 21 + 41 =

17. 222 – 22 + 41 =
232 – 23 + 41 =
242 – 24 + 41 =
252 – 25 + 41 =
262 – 26 + 41 =
272 – 27 + 41 =
282 – 28 + 41 =

18. 292 – 29 + 41 =
302 – 30 + 41 =
312 – 31 + 41 =
322 – 32 + 41 =
332 – 33 + 41 =
342 – 34 + 41 =
352 – 35 + 41 =

19. 362 – 36 + 41 =
372 – 37 + 41 =
382 – 38 + 41 =
392 – 39 + 41 =
402 – 40 + 41 =
412 – 41 + 41 = = 412

20.
() X = 1 q – 1
q =
1 + d
4

21. X2 – X + X = 1
X2 – X + X = 1, 2
X2 – X + X = 1, 2, 3, 4, 5
X2 – X + X = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
X2 – X + X = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
X2 – X + X = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …, 40

22. e⇡
p
163
= 262537412640768743.99999999999925...
12 digits

23. Google

24.
e⇡
p
d
e⇡
p
d
= ( )3 + 744 – ( )

25. e⇡
p
19
= 963
+ 744 - 0.22 . . .
e⇡
p
43
= 9603
+ 744 - 0.00022 . . .
e⇡
p
67
= 52803
+ 744 - 0.0000013 . . .

26. e⇡
p
163
163
= 6403203
+ 744 - 0.00000000000075 . . .
12 digits

27.
e⇡
p
d
() X = 1 q – 1

30. Q(
p
-d)
()
(=))
((=)
(1912 )
(1913 )
X = 0, · · · , q - 2
X2
+ X + q
tsujimotter
http://tsujimotter.hatenablog.com/entry/prime-generating-polynomials

31. j(⌧) =
1
q
+ 744 + 196884q + 21493760q3
+ · · ·
j- q-
⌧ =
1 +
p
-d
2
q = -
1
e⇡
p
d
e⇡
p
d
= -j
✓
1 +
p
-d
2
◆
+ 744 - 196884
✓
1
e⇡
p
d
◆
- 21493760
✓
1
e⇡
p
d
◆3
- · · ·

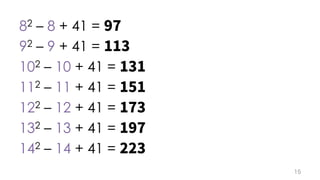
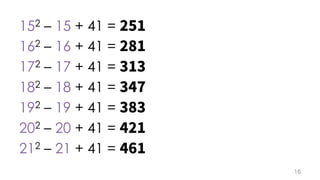
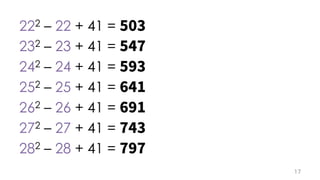
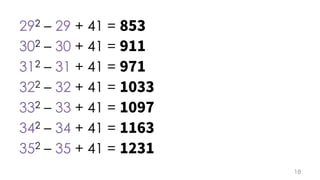
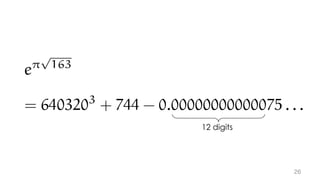
32. Romantic formula
1
⇡
=
12
6403203/2
1X
k=0
(6k)!(163 · 3344418k + 13591409)
(3k)!(k!)3(-640320)3k
j
✓
1 +
p
-163
2
◆
= -6403203
[Chudnovsky brothers 1989]

33. Heegner Number
Q(
p
-d) Heegner Number h log " - 32
21 ⇡
p
d < e
⇡
p
d
100
h0
log "0
- 80
33 ⇡
p
d < e
⇡
p
d
100
---- (1)
---- (2)
(1), (2) |b log " + b0
log "0
| < e- B
B <
⇣
4n2
-1
l2n
log A
⌘(2n+1)2
< 10250
⇣
B = 140
p
d
⌘
) d < 10500
(A)

34. Heegner Number
Heilbronn, Linfoot
10 Heegner Number d > e1000000
(B)
d
(B)(A)
d > e1000000) d < 10500
d (QED)
tsujimotter
http://tsujimotter.hatenablog.com/entry/class-numbers-of-imaginary-quadratic-fields