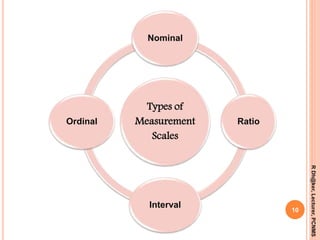
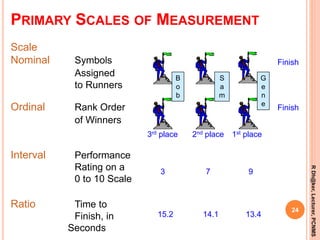
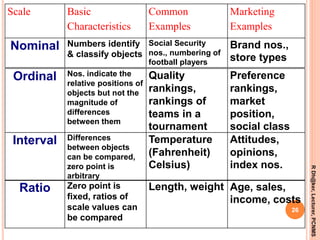
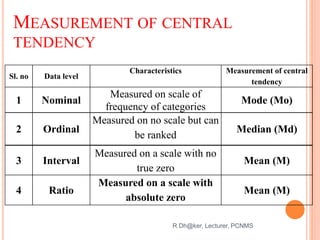
This document provides an introduction to statistics and biostatistics. It discusses key concepts including: - The definitions and origins of statistics and biostatistics. Biostatistics applies statistical methods to biological and medical data. - The four main scales of measurement: nominal, ordinal, interval, and ratio scales. Nominal scales classify data into categories while ratio scales allow for comparisons of magnitudes and ratios. - Descriptive statistics which organize and summarize data through methods like frequency distributions, measures of central tendency, and graphs. Frequency distributions condense data into tables and charts. Measures of central tendency include the mean, median, and mode.

1. INTRODUCTION
TO
STATISTICS
R Dh@ker, Lecturer, PCNMS 1

2. INTRODUCTION
The word statistics conveys a variety of
meaning to people in different walks of life.
2R Dh@ker, Lecturer, PCNMS
The word statistics comes from the Italian
words Statista
( Statement).

3. CONT…INTRODUCTION
The German word Statistik
3
RDh@ker,Lecturer,PCNMS
Political state
The word Statistics today refers to either
quantitative information or a method of
delaling with quantitative or qualitative
information.

4. DEFINITION
“Statistics is defined as collection, Presentation,
analysis and interpretation of numerical data”.
Acc. Croxton & cowden
4
RDh@ker,Lecturer,PCNMS
statistics is the sciences and art of dealing with
figure and facts.

5. Biostatistics is the branch of statistics
applied to biological or medical sciences.
Biostatistics is the methods used in dealing
with statistics in the field of health sciences
such as biology, medicine, nursing, public
health etc.
5
RDh@ker,Lecturer,PCNMS

6. Biostatistics is the branch of statistics
applied to biology or medical sciences.
Biostatistics is also called “Biometry”
6
RDh@ker,Lecturer,PCNMS
In Greek, Bios Life
Metron
So, it is measurement of life
Measured

7. USE & APPLICATION OF STATISTICS
It facilitates comparisons
It simplifies the message of figure
It helps in formulating and testing hypothesis
It help in prediction
7
RDh@ker,Lecturer,PCNMS

8. SCALE OF MEASUREMENT
 Measurement is the process of assigning numbers
or labels to objects, persons, states, or events in
accordance with specific rules to represent
quantities or qualities of attributes.
 We do not measure specific objects, persons, etc.,
we measure attributes or features that define them.
8
RDh@ker,Lecturer,PCNMS

9. Nominal Scales
Ordinal Scales
Interval Scales
Ratio Scales
FOUR BASIC SCALES OF MEASUREMENT
9
RDh@ker,Lecturer,PCNMS

10. Types of
Measurement
Scales
Nominal
Ratio
Interval
Ordinal
10
RDh@ker,Lecturer,PCNMS

11. There must be distinct classes but these classes
have no quantitative properties. Therefore, no
comparison can be made in terms of one category
being higher than the other.
For example - there are two classes for the
variable gender - males and females. There are
no quantitative properties for this variable or
these classes and, therefore, gender is a nominal
variable.
11
RDh@ker,Lecturer,PCNMS

12. CONT…NOMINAL SCALE
Sometimes numbers are used to designate
category membership-
Example:
Country of Origin
1 = United States 3 = Canada
2 = Mexico 4 = Other
12
RDh@ker,Lecturer,PCNMS

13. There are distinct classes but these classes have a
natural ordering or ranking. The differences can be
ordered on the basis of magnitude.
For example - final position of horses in a
thoroughbred race is an ordinal variable. The horses
finish first, second, third, fourth, and so on. The
difference between first and second is not
necessarily equivalent to the difference between
second and third, or between third and fourth. 13
RDh@ker,Lecturer,PCNMS
Ordinal Scales

14. CONT…ORDINAL SCALES
 Does not assume that the intervals between numbers
are equal
Example:
finishing place in a race
(first place, second place)
1 hour 2 hours 3 hours 4 hours 5 hours 6 hours 7 hours 8 hours
1st place 2nd place 3rd place 4th place
14
RDh@ker,Lecturer,PCNMS

15. INTERVAL SCALES
It is possible to compare differences in magnitude,
but importantly the zero point does not have a
natural meaning. It captures the properties of
nominal and ordinal scales - used by most
psychological tests.
Designates an equal-interval ordering - The
distance between, for example, a 1 and a 2 is the
same as the distance between a 4 and a 5
15
RDh@ker,Lecturer,PCNMS

16. We can see that the same difference
exists between 10o C ( 50 F) and 20
degree C ( 68 F)
25 C ( 77F) and 35 C ( 95 F)
But we can not say that 20C is twice as
hot as a temperature of 10C
16
RDh@ker,Lecturer,PCNMS

17. RDh@ker,Lecturer,PCNMS
17
Example - Celsius temperature is an interval
variable. It is meaningful to say that 25 degrees
Celsius is 3 degrees hotter than 22 degrees Celsius,
and that 17 degrees Celsius is the same amount
hotter (3 degrees) than 14 degrees Celsius. Notice,
however, that 0 degrees Celsius does not have a
natural meaning. That is, 0 degrees Celsius does not
mean the absence of heat!

18. RATIO SCALES
It is the highest level for measurement
This level has all the three attributes:
 Magnitude
 Equal interval
 Absolute zero point
It represent continuous values
18
RDh@ker,Lecturer,PCNMS

19.  Example:
 Biophysical parameters
Weight
Height
Volume
Blood pressure
19
RDh@ker,Lecturer,PCNMS

20. 30 Kg is thrice of 10 kg
20 cm is twice of 10 cm
8 hours is four time of 2 hours
20
RDh@ker,Lecturer,PCNMS

21. TYPES OF MEASUREMENT SCALES
(CONT.)
Each of these scales have different properties
(i.e., difference, magnitude, equal intervals, or
a true zero point) and allows for different
interpretations.
21
RDh@ker,Lecturer,PCNMS

22. The scales are listed in hierarchical order.
Nominal scales have the fewest measurement
properties and ratio having the most properties
including the properties of all the scales beneath
it on the hierarchy.
22
RDh@ker,Lecturer,PCNMS
TYPES OF MEASUREMENT SCALES (CONT.)

23. The goal is to be able to identify the type of
measurement scale, and to understand proper
use and interpretation of the scale.
23
RDh@ker,Lecturer,PCNMS
TYPES OF MEASUREMENT SCALES (CONT.)

24. B
o
b
G
e
n
e
S
a
m
PRIMARY SCALES OF MEASUREMENT
Scale
Nominal Symbols
Assigned
to Runners
Ordinal Rank Order
of Winners
Interval Performance
Rating on a
0 to 10 Scale
Ratio Time to
Finish, in
Seconds
3rd place 2nd place 1st place
Finish
Finish
3 7 9
15.2 14.1 13.4
24
RDh@ker,Lecturer,PCNMS

25. 26
RDh@ker,Lecturer,PCNMS
Scale Basic
Characteristics
Common
Examples
Marketing
Examples
Nominal Numbers identify
& classify objects
Social Security
nos., numbering of
football players
Brand nos.,
store types
Ordinal Nos. indicate the
relative positions of
objects but not the
magnitude of
differences
between them
Quality
rankings,
rankings of
teams in a
tournament
Preference
rankings,
market
position,
social class
Interval Differences
between objects
can be compared,
zero point is
arbitrary
Temperature
(Fahrenheit)
Celsius)
Attitudes,
opinions,
index nos.
Ratio Zero point is
fixed, ratios of
scale values can
be compared
Length, weight Age, sales,
income, costs

26.  Descriptive statisticsuse to organize and summarize the data to draw
meaningful interpretations.
 Descriptive statisticsdeal with the enumeration, organization and graphical
representation of data.
R Dh@ker, Lecturer, PCNMS
27

27. CONT…DESCRIPTIVE STATISTICS
 Descriptive statistics includes-
 Measures to condense data
 Measures of central tendency
 Measures of dispersion
 Measures of relationship ( Correlation coefficient)
R Dh@ker, Lecturer, PCNMS
28

28. Measures to condense data
 Frequency and percentage distribution through tabulation and graphic presentation.
 Table
 Graphsand diagrams
 Percentages
R Dh@ker, Lecturer, PCNMS 29

29.  Type
 Frequency distributiontable
 Contingency table
 MultipleResponsetable
 Miscellaneoustable
R Dh@ker, Lecturer, PCNMS
30

30. FREQUENCY DISTRIBUTION TABLE
 The data may be qualitative or quantitative
31
RDh@ker,Lecturer,PCNMS

31. The following are the weight in kg 48
medical students. Construct the
frequency distribution table
50, 61, 70 71 63 34 75 80 45 56 57 58
60 62 72 78 48 50 63 64 67 52 52 54
55 56 57 70 71 72 73 64 65 66 67 62
63 65 52 60 54 56 58 57 61 81 82 80
32
RDh@ker,Lecturer,PCNMS

32. RELATIVE FREQUENCY
 Relative frequency =
Class frequency
---------------------------
Total frequency
33
RDh@ker,Lecturer,PCNMS

33. FREQUENCY DENSITY OF A CLASS
 Frequency density of a class=
frequency of the class
-------------------------------
width of the class
34
RDh@ker,Lecturer,PCNMS

34. 105 100 109 106 122 103 122 107 102
105 103 100 119 116 120 122 115 119
118 109 103 108 106 107 104 103 105
102 106 103 109 114 122 114 100 116
115 110 120 100 117 120 107 116 119
122 122 107 106 117
35
RDh@ker,Lecturer,PCNMS

35. 138 164 150 132 144 125 149 157
146 158 140 109 136 148 152 144
168 126 138 186 163 109 154
165 146 183 105 108 135 153
140 135 161 145 135 142 150
156 145 128
36
RDh@ker,Lecturer,PCNMS

36.  Type
 Bar diagram
 Pie chart
 Histogram
 Frequency polygon
 Line diagram
R Dh@ker, Lecturer, PCNMS
37
Cumulative frequency curve
Scattered diagram
Pictograms
Map diagrams

37. CONT…GRAPHS AND DIAGRAMS
 Presentation of quantitative, continuous or measured
data is through graphs. The common graphs in use
are:-
 Histogram
 Frequency polygon
 Frequency curve
 Line chart or graph
 Cumulative frequency diagram
 Scatter or dot diagram
R Dh@ker, Lecturer, PCNMS
38

38.  Presentation of qualitative , discrete or counted data is
through diagrams. The common diagrams in use are:-
 Bar diagram
 Pie diagram
 Pictogram diagram
 Map diagram or spot map
R Dh@ker, Lecturer, PCNMS
39
CONT…Graphs and diagrams

39. Measures of central tendency
Arithmeticmean
Median
Mode
Geometric mean
R Dh@ker, Lecturer, PCNMS
40

40. MEASUREMENT OF CENTRAL
TENDENCY
R Dh@ker, Lecturer, PCNMS 41
Sl. no Data level
Characteristics Measurement of central
tendency
1 Nominal
Measured on scale of
frequency of categories
Mode (Mo)
2 Ordinal
Measured on no scale but can
be ranked
Median (Md)
3 Interval
Measured on a scale with no
true zero
Mean (M)
4 Ratio
Measured on a scale with
absolute zero
Mean (M)

41. 42
RDh@ker,Lecturer,PCNMS