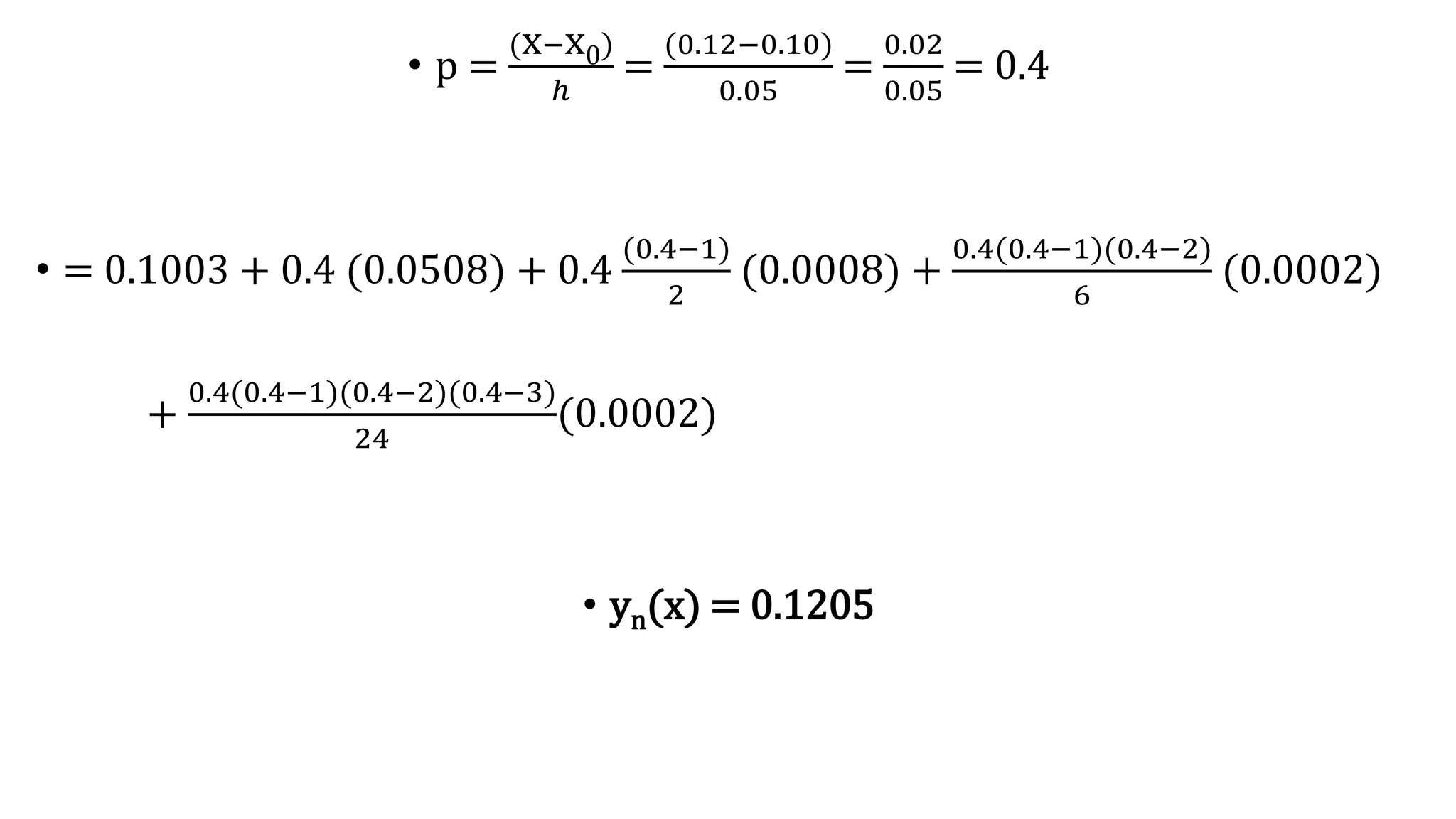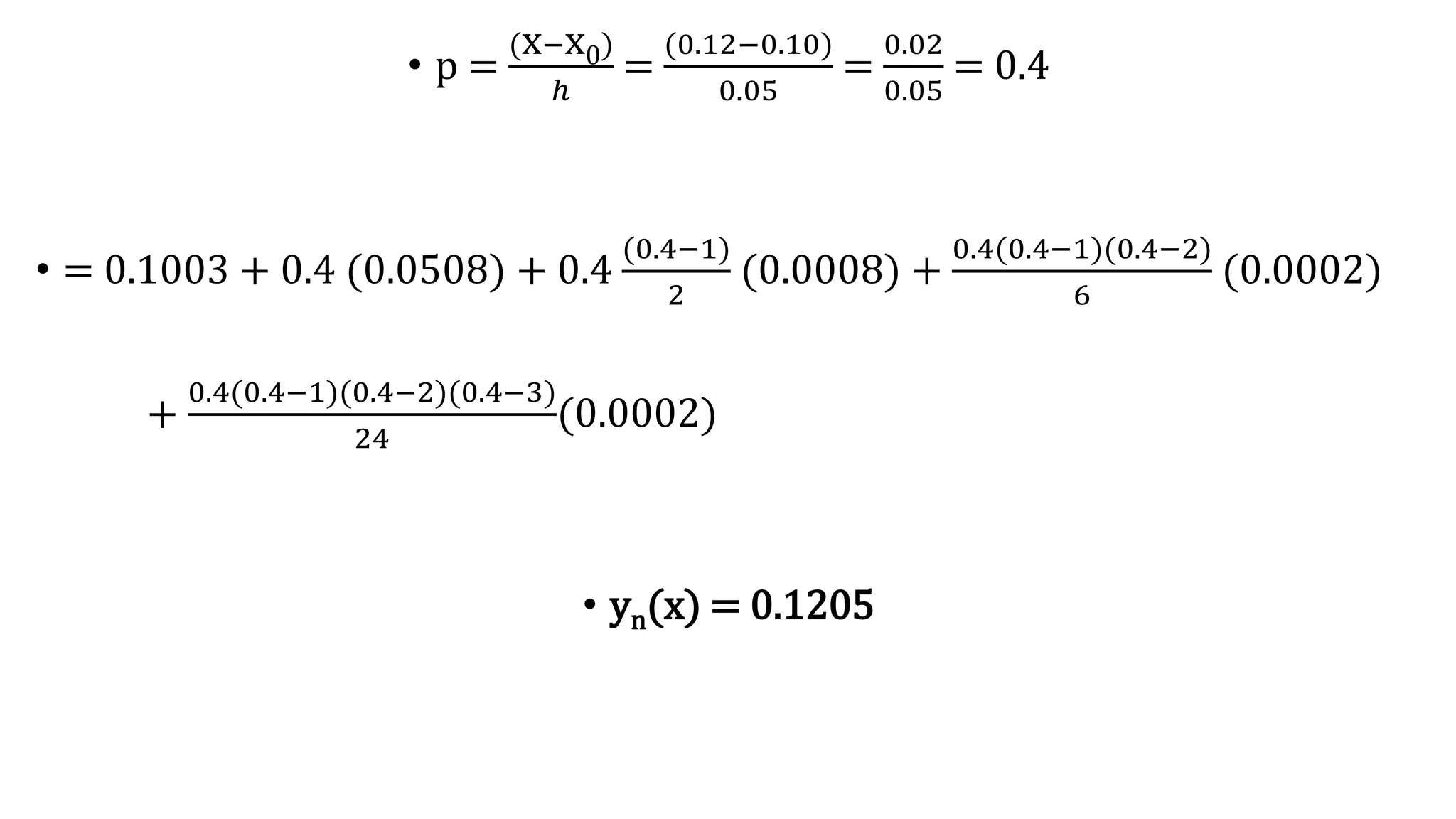
This document provides Newton's formula for forward difference interpolation and an example of using it to find the value of tan(0.12). - Newton's formula uses forward difference interpolation to find the value of a polynomial of degree n that fits a set of (n+1) equally spaced (x,y) points. - The coefficients of the polynomial are determined using forward differences of the y-values. - In the example, the value of tan(0.12) is found by applying Newton's formula to a table of tan(x) values from 0.10 to 0.30 using forward differences up to degree 4.

1. Newton’s Forward Difference
Interpolation (Method + Example)
Name: Raj Parekh
Enrollment no: 140990119029
Sub: CVNM

2. Newton’s Formula For Forward Difference Interpolation.
• Given that set of (n+1) values (x0,y0),(x1,y1) ,…, (xn,yn) of x and y.
• To obtain yn(x), polynomial of the nth degree.
• If the arguments x0,x1 ,…,xn are equally spaced, then
xi = x0+ih, i = 0,1,2,…,n
Since yn(x) is a polynomial of the nth degree, it may be written as
yn(x) = a0+ a1(x-x0)+ a2(x-x0) (x-x1)+ a3(x-x0) (x-x1) (x-x2)+… + an(x-x0)(x-x1)(x-x2)…
(x-xn-1)
By putting x = x0,x1, … respectively yn(x0) = y0, yn(x1) = y1,….

3. • But y and yn(x) should agree at the set of tabulated points.
• We have
a0 = y0 , a1 =
y1−y0
x1−x0
=
Δy0
ℎ
, a2 =
Δ2y0
h22!
,…
a3 =
Δ3y0
h33!
,… an =
Δny0
h3n!
• Setting x = x0 + ph and substituting for a0,a1, …., an, equation becomes
yn(x) = y0 + pΔy0 +
𝑝(𝑝−1)
2!
Δ2y0 +
𝑝(𝑝−1)(𝑝−2)
3!
Δ3y0+ … +
𝑝 𝑝−1 𝑝−2 …(𝑝−𝑛+1)
𝑛!
Δny0
• The above equation is Newton’s Forward difference interpolation formula.

4. • Example: Find the value of tan 0.12
• Solutin :
The table of difference is
x 0.10 0.15 0.20 0.25 0.30
y = tan x 0.1003 0.1511 0.2027 0.2553 0.3093
x y Δ Δ2 Δ3 Δ4
0.10 0.1003
0.0508
0.15 0.1511 0.0008
0.0516 0.0002
0.20 0.2027 0.0010 0.0002
0.0526 0.0004
0.25 0.2553 0.0014
0.0540
0.30 0.3093

5. • Here to obtain the value of tan (0.12), the value of 0.12 is near the beginning of a set of tabular
values.
• Therefore, Applying Newton’s Forward Difference Interpolation Formula
• i.e.
• yn(x) = y0 + pΔy0 +
𝒑(𝒑−𝟏)
𝟐!
Δ2y0 +
𝒑(𝒑−𝟏)(𝒑−𝟐)
𝟑!
Δ3y0+ … +
𝒑 𝒑−𝟏 𝒑−𝟐 …(𝒑−𝒏+𝟏)
𝟒!
Δ4y0
• Here , yn(x) = tan(0.12)
y0 = 0.1003 Δy0 = 0.0508 Δ2y0 = 0.0008
Δ3y0 = 0.0002 Δ4y0 = 0.0002

6. • p =
(x−x0)
ℎ
=
(0.12−0.10)
0.05
=
0.02
0.05
= 0.4
• = 0.1003 + 0.4 (0.0508) + 0.4
(0.4−1)
2
(0.0008) +
0.4(0.4−1)(0.4−2)
6
(0.0002)
+
0.4(0.4−1)(0.4−2)(0.4−3)
24
(0.0002)
• yn(x) = 0.1205

7. THANK YOU