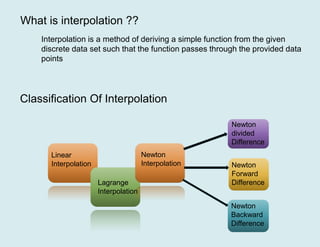
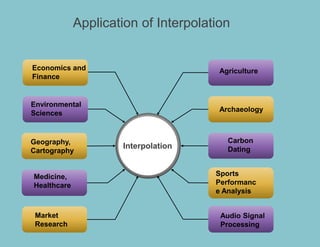
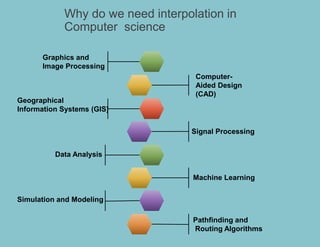
The document provides information about different types of interpolation methods: 1) Linear interpolation uses a straight line to estimate missing data points between two known points. 2) Lagrange interpolation uses a polynomial function that passes through multiple provided data points. 3) Newton's divided difference method finds the coefficients of a polynomial function using a divided difference process to estimate unknown values within a given range. 4) Newton's forward and backward interpolation formulas are used to interpolate values nearer to the beginning or end of a data table when the difference in the independent variable is constant.

1. Interpolation
1
Crazy Hair
Day
Tuesday
2
Sports
Day
Wednesday
3
Pajama
Day
Thursday
4
Superhero
Day
Friday
5
School
Pride Day

2. Group member
Rita Faria
Richi
ID : 221-15-5025
1
MD. Moinur
Hasan
ID : 221-15-5692
3
ID : 221-15-5356
4
MD. Al –
Razi
Talukdar
ID : 221-15-5822
5
MD. Bilayet
Hossain

3. Classification Of Interpolation
Linear
Interpolation
Lagrange
Interpolation
Newton
Interpolation
Interpolation is a method of deriving a simple function from the given
discrete data set such that the function passes through the provided data
points
What is interpolation ??
Newton
divided
Difference
Newton
Forward
Difference
Newton
Backward
Difference

4. Linear Interpolation
Linear interpolation is a basic method that uses a straight line to estimate line
to estimate missing data points .
Given the two red points, the blue line is the linear interpolant
between the points, and the value y at x may be found by linear
interpolation.
Formula:
𝑦=𝑦1+(𝑥−𝑥1)((𝑦2−𝑦1))/((𝑥2−𝑥1))

5. Lagrange Interpolation
Lagrange interpolation is a method for estimating unknown values of a function within a
given range using a polynomial function.
Derivation of 2nd order Lagrange interpolation
Step -1 :
In this case ,select three points from the data set: (x0,y0), (x1,y1), and
(x2,y2).Using the Lagrange polynomial equation, create a polynomial that passes
through these three points.
The Lagrange interpolation method involves
using a polynomial of degree n to approximate
a function using n+1 data points.
Step -2: Consider a 2nd order polynomial of the form -

6. Step -3: :
Let,(x0,f0), (x1,f1), and (x2,f2) are 3 points are on the
curve ,thenI figured out the value of the three b0,b1,b2
Step-4: After replacing b0,b1,b2 in first equation
When 1st order Lagrange is a linear interpolation consider n=1 and here we
use two points X0,X1. solving this equation we get that,
Which is a linear interpolation function .

7. Newton divided difference
The Newton divided difference method is a way to find the
coefficients of a polynomial function using the divided difference
process.
Newton’s divided difference formula is given by:

8. Estimate f(2) from the following data, using Newton’s
divided differences method.
Solution :
1. Firstly, why should I use newton’s divided difference method here .
here ,the difference between two x value is not same that’s why I use this method .
2. Then we calculate First ,2nd and 3rd difference for this data collection .here we
show the difference table….

9. 3. Newton’s divided difference formula is given by:
4. From the table , we get this type of value …
Since this table is created by f(2) that’ why, we can use x=2
5. Substituting these values in equation (1) ,
we get

10. Newton’s Forward
Interpolation
Forward interpolation formula is used to interpolate the values of y nearer to the
beginning value of the given table. Also this formula is applicable if in case where
x (difference in in travel) is constant.
Newton’s forward interpolation formula is given by:
Where

11. Newton’s Backward
Interpolation
Newton's Backward Difference Interpolation is a method used to estimate the value
of a function at a particular point based on a set of discrete data points.
Newton’s backward interpolation formula is given by:
Where,

12. Application of Interpolation
Interpolation
Economics and
Finance
Environmental
Sciences
Geography,
Cartography
Medicine,
Healthcare
Market
Research
Agriculture
Archaeology
Sports
Performanc
e Analysis
Carbon
Dating
Audio Signal
Processing

13. Why do we need interpolation in
Computer science
Graphics and
Image Processing
Computer-
Aided Design
(CAD)
Geographical
Information Systems (GIS)
Signal Processing
Data Analysis
Machine Learning
Simulation and Modeling
Pathfinding and
Routing Algorithms

14. Thank you