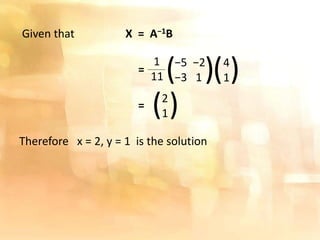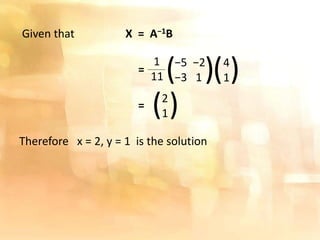
This document discusses two methods for solving systems of linear equations: 1) The inverse matrix method, which involves writing the system in matrix form AX = B and solving for X by computing A-1B, where A-1 is the inverse of the coefficient matrix A. 2) Cramer's rule, which uses determinants to find the values of the variables by taking ratios of determinants formed from the coefficients and constants. The method works by solving one variable at a time.

1. Solving System of Linear
Equations Methods
Presented by:
Aornwara Nitkhosakul No.1
M.4/1

2. Inverse Matrix Method
Given a set of linear equations
x + 2y = 4
3x − 5y = 1
It can be written in matrix form as…
=
AX = B
This is the matrix form of the linear equations
1 2
3 −5( ) x
y( ) 4
1( )

3. Given that…
AX = B
A-1AX = A-1B
(A−1A = I, the identity matrix and multiplying any matrix
by I leaves the matrix unchanged)
X = A−1B

4. Example: x + 2y = 4
3x − 5y = 1
=
Find A-1
A- 1 = (adjoint of A)
=
=
1 2
3 −5( ) x
y( ) 4
1( )
1
(1)(−5) − (2)(3)
−5 −2
−3 1( )
1
det A
1
11
−5 −2
−3 1( )

5. Given that X = A−1B
=
=
Therefore x = 2, y = 1 is the solution
1
11
−5 −2
−3 1( ) 4
1( )
2
1( )

6. Cramer's Rule
Given a set of linear equations
3x + 4y = −14 2x + y + z = 3
−2x − 3y = 11 x – y – z = 0
x + 2y + z = 0
It can be written as..
a1x + b1y = d1 a1x + b1y + c1z = d1
a2x + b2y = d2 a2x + b2y + c2y = d2
a3x + b3y + c3z = d3
(a, b, c are coefficients while d is the solution )
It is a method of solving linear equations by using
determinants

7. Where l...l is the determinant
The values of x, y and z can be found from…
X = Y =
d1 b1
d2 b2
a1 b1
a2 b2
a1 d1
a2 d2
a1 b1
a2 b2

8. Example: 2x + y + z = 3
x – y – z = 0
x + 2y + z = 0
Finding x
x = x = = 1
3 1 1
0 -1 -1
0 2 1
2 1 1
1 -1 -1
1 2 1
3
3

9. Finding y
y= = = -2
Finding z
z= = = 3
Therefore x = 1, y = -2 , z = 3 is the solution
2 3 1
1 0 -1
1 0 1
2 1 1
1 -1 -1
1 2 1
-6
3
2 1 3
1 -1 0
1 2 0
2 1 1
1 -1 -1
1 2 1
9
3

10. Notes
• If the coefficient determinant is zero
– It means that the system of equations has no
unique solution
– The system may has no solution at all or an infinite
solution
• The coefficient matrix of the system must be
square