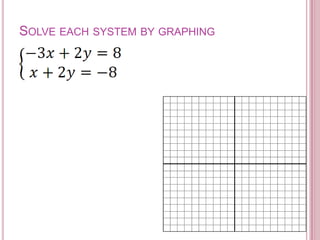
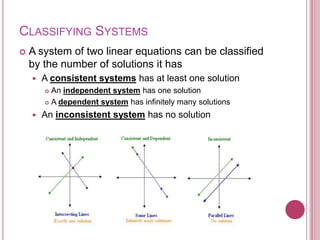
This document summarizes different methods for solving systems of linear equations, including graphing, substitution, and elimination. It discusses classifying systems as independent, dependent, or inconsistent based on the number of solutions. Examples are provided to illustrate solving systems by graphing, substitution, and elimination.

1. Chapter 3 Linear Systems 3.1 Solving Systems Using Tables and Graphs3.2 Solving Systems Algebraically

2. System of Equations A system of equations is a set of two or more equationsA linear system consists of linear equationsA solution of a system is a set of values for the variables that makes all the equations true. (usually an ordered pair)Systems can be solved be various methods: graphing, substitution, and elimination

3. Solving a system by graphingWrite each equation in slope-intercept formGraph each lineFind the point of intersection (this is your solution)Check by substituting the values into both equations

4. Solve each system by graphing

5. Classifying SystemsA system of two linear equations can be classified by the number of solutions it hasA consistent systems has at least one solutionAn independent system has one solutionA dependent system has infinitely many solutionsAn inconsistent system has no solution

6. Without graphing, classify each system as independent, dependent, or inconsistentRewrite each equation into slope-intercept formCompare the slopes and y-interceptsDifferent slopes: independent systemSame slope and same y-intercept: dependent systemSame slope and different y-intercept: inconsistent

7. Without graphing, classify each system as independent, dependent, or inconsistent

8. Without graphing, classify each system as independent, dependent, or inconsistent

9. Solving Systems by SubstitutionSolve one equation for one of the variablesSubstitute the expression into the other equation and solveSubstitute the solution into one of the original equations and solve for the remaining variableCheck the solution

10. Solving Systems by SubstitutionUse when it is easy to isolate one of the variables

11. Solving by EliminationRewrite both equations in standard formMultiply one or both systems by an appropriate non-zero number (note you want one variable to drop out in the next step)Add the equationsSolve for the variableSubstitute the value into one of the original equation and solve for the remaining variableCheck the solution

12. Solve by elimination

13. Solving systems without unique SolutionsSolving a system algebraically can sometimes lead to infinitely many solutions and/or no solutionIf you get a true result: infinitely many solutionsIf you get a false result: no solution

14. Example: Solve the system

15. Example: Solve the system