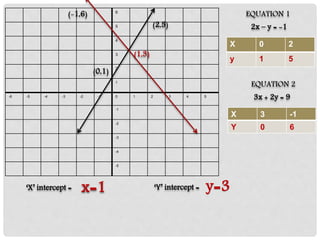
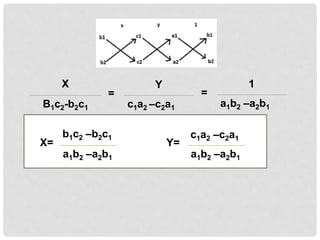
i) The document discusses various methods for solving systems of linear equations, including graphing, substitution, elimination, and cross-multiplication. ii) It also addresses solving systems that can be reduced to linear equations, such as transforming non-linear equations using substitution. iii) Examples are provided to illustrate each method for deriving the solution of a system of equations.

1. I N C L U D E S S AM P L E P R O B L E M S
ULTIMATE GUIDE TO SOLVING
SYSTEMS OF EQUATIONS

2. Table of Contents:
Introduction
Solving Systems by Graphing
Solving Systems by Substitution
Solving Systems by Elimination
Special Cases
Summary

3. INTRODUCTION TO
SYSTEMS OF EQUATIONS
A pair of linear equations is said to form a system of
linear equations in the standard form
a1x+b1y+c1=0
a2x+b2y+c2=0
Where ‘a’, ‘b’ and ‘c’ are not equal to real numbers ‘a’
and ‘b’ are not equal to zero.

4. OBTAINING THE SOLUTION BY
GRAPHING
Let us consider the following system of two simultaneous linear
equations in two variable.
2x – y = -1 ;3x + 2y = 9
We can determine the value of the a variable by substituting
any value for the other variable, as done in the given examples
X 0 2
Y 1 5
X 3 -1
Y 0 6
X=(y-1)/2 y=2x+1 2y=9-3x x=(9-2y)/3
2x – y = -1 3x + 2y = 9

5. 6
5
4
3
2
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
-1
-2
-3
-4
-5
(1,3)
(2,5)
(-1,6)
(0,1)
x=1
X 0 2
y 1 5
X 3 -1
Y 0 6
EQUATION 1
EQUATION 2
‘X’ intercept = ‘Y’ intercept =
2x – y = -1
3x + 2y = 9
y=3

6. ax1 + by1 + c1 = 0;
ax2 + by2 + c2 = 0
a1 b1 c1
c2a2 b2
=i)
ii)
iii)
=
a1 b1
a2 b2
=
a1 b1 c1
c2a2 b2
==
Intervening Lines; Infinite Solutions
Intersecting Lines; Definite Solution
Parallel Lines; No Solution

7. DERIVING THE SOLUTION THROUGH
SUBSTITUTION METHOD
This method involves substituting the value of one
variable, say x , in terms of the other in the
equation to turn the expression into a Linear
Equation in one variable.
For example
x + 2y = -1 ;
2x – 3y = 12

8. 2x – 3y = 12 ----------(ii)
x = -2y -1
x = -2 x (-2) – 1
= 4–1
x = 3
x + 2y = -1 -------- (i)
x + 2y = -1
x = -2y -1 ------- (iii)
Substituting the value of x
inequation (ii), we get
2x – 3y = 12
2 ( -2y – 1) – 3y
= 12 - 4y – 2 – 3y
= 12 - 7y = 14
= 12 - 14 = 7y
y = -2
Putting the value of y
in eq. (iii), we get
The solution of the equation is ( 3, - 2 )

9. DERIVING THE SOLUTION THROUGH
ELIMINATION METHOD
In this method, we eliminate one of the two variables to
obtain an equation in one variable which can easily be
solved. The value of the other variable can be obtained by
putting the value of this variable in any of the given
equations.
For example:
3x + 2y = 11 ;2x + 3y = 4

10. 3x + 2y = 11 --------- (i) 2x + 3y = 4 ---------(ii)
3x + 2y = 11 x3-
9x - 3y = 33---------(iii)
=>9x + 6y = 33-----------(iii)
4x + 6y = 8------------(iv)
(-) (-) (-)
(iii) – (iv) =>
x3 2x + 3y = 4
4x + 6y = 8---------(ii)
x2
5x = 25
x = 5
Putting the value of x in
equation (ii) we get, =>
2x + 3y = 4
2 x 5 + 3y = 4
10 + 3y = 4
3y = 4 – 10
3y = - 6
y=-2
Hence, x = 5 and y = -2

11. DERIVING THE SOLUTION THROUGH THE
CROSS-MULTIPLICATION METHOD
The method of obtaining solution of simultaneous equation by using
determinants is known as Cramer’s rule. In this method we have to follow
this equation and diagram
ax1 + by1 + c1 = 0;
ax2 + by2 + c2 = 0
b1c2 –b2c1
a1b2 –a2b1
c1a2 –c2a1
a1b2 –a2b1
X=
Y=

12. X
B1c2-b2c1
Y
c1a2 –c2a1
=
1
a1b2 –a2b1
=
b1c2 –b2c1
a1b2 –a2b1
c1a2 –c2a1
a1b2 –a2b1
X= Y=

13. Example:
8x + 5y – 9 = 0 3x + 2y – 4 = 0
X
-20-(-18)
Y
-27-(-32)
=
1
16-15
=
X Y 1
1-2 5
=
X
-2
Y
5
=1 1
X = -2 and Y = 5
X
B1c2-b2c1
Y
c1a2 –c2a1
=
1
a1b2 –a2b1
=

14. EQUATIONS REDUCIBLE TO A PAIR OF
LINEAR EQUATIONS IN TWO VARIABLES
In case of equations which are not linear, like
We can turn the equations into linear equations by substituting
2 3
13
x y
=
5 4
-2
x y
=+ -
1
p
x
=
1
q
y
=

15. The resulting equations are
2p + 3q = 13 ; 5p - 4q = -2
These equations can now be solved by any of the
aforementioned methods to derive the value of ‘p’ and
‘q’.
‘p’ = 2 ;‘q’ = 3
We know that
1
p
x
=
1
q
y
=
1
X
2
=
1
Y
3
=
&

16. SUMMARY
• Insight to Pair of Linear Equations in Two Variable
• Deriving the value of the variable through
• Graphical Method
• Substitution Method
• Elimination Method
• Cross-Multiplication Method
• Reducing Complex Situation to a Pair of Linear Equations to
derive their solution