Watanabe理論勉強会 第二回 発表資料

1. シンギュラリティを知らずに
機械学習を語るな
@hoxo_m
2016/09/25
1

2. 自己紹介
• hoxo_m
• 所属：匿名知的集団ホクソエム
付録C
2

3. 本日のお話
• Sumio Watanabe says:
• “It is not until we understand
singularities that we obtain
statistical learning theory”
• 「シンギュラリティを理解してはじめて
統計的学習理論が身についたと言える」
3

4. シンギュラリティ?
• IQの分布
人工
知能
IQ 10000IQ 100
4

5. シンギュラリティ?
• IQの分布
人工
知能
IQ 10000IQ 100
※これではない
5

6. Singularity (特異性)
• 数学において、特異性(singularity)とは、
適当な枠組みの下で考えている数学的対
象が「定義されない」「よく振舞わな
い」などと言ったことを理由に除外され
ること、もの、およびその基準である。
特異性を示す点を特異点(singular point)
という。
特異点(数学) – Wikipedia より
6

7. Watanabe理論勉強会 #2
• 本資料は
• Sumio Watanabe, Algebraic Geometry
and Statistical Learning Theory,
Cambridge University Press, 2009.
• 第2回読書会資料です。
7

8. 前回(第1章)
• E[min Kn(w)] ≠ min E[Kn(w)] = min K(w)
• 尤度の最大化はカルバック・ライブラー
距離の最小化を意味しない
• これが、統計的学習が単純な最適化問題
にならない理由である
• Watanabe理論恐ろしい・・(ﾟДﾟ;)
8

9. 第2章 Singularity Theory
• 担当分
2.1 Polynomials and analytic functions
(多項式と解析関数の定義)
2.2 Algebraic set and analytic set
(代数的集合と解析的集合の定義)
2.3 Singularity
(特異点の定義と判別法)
9

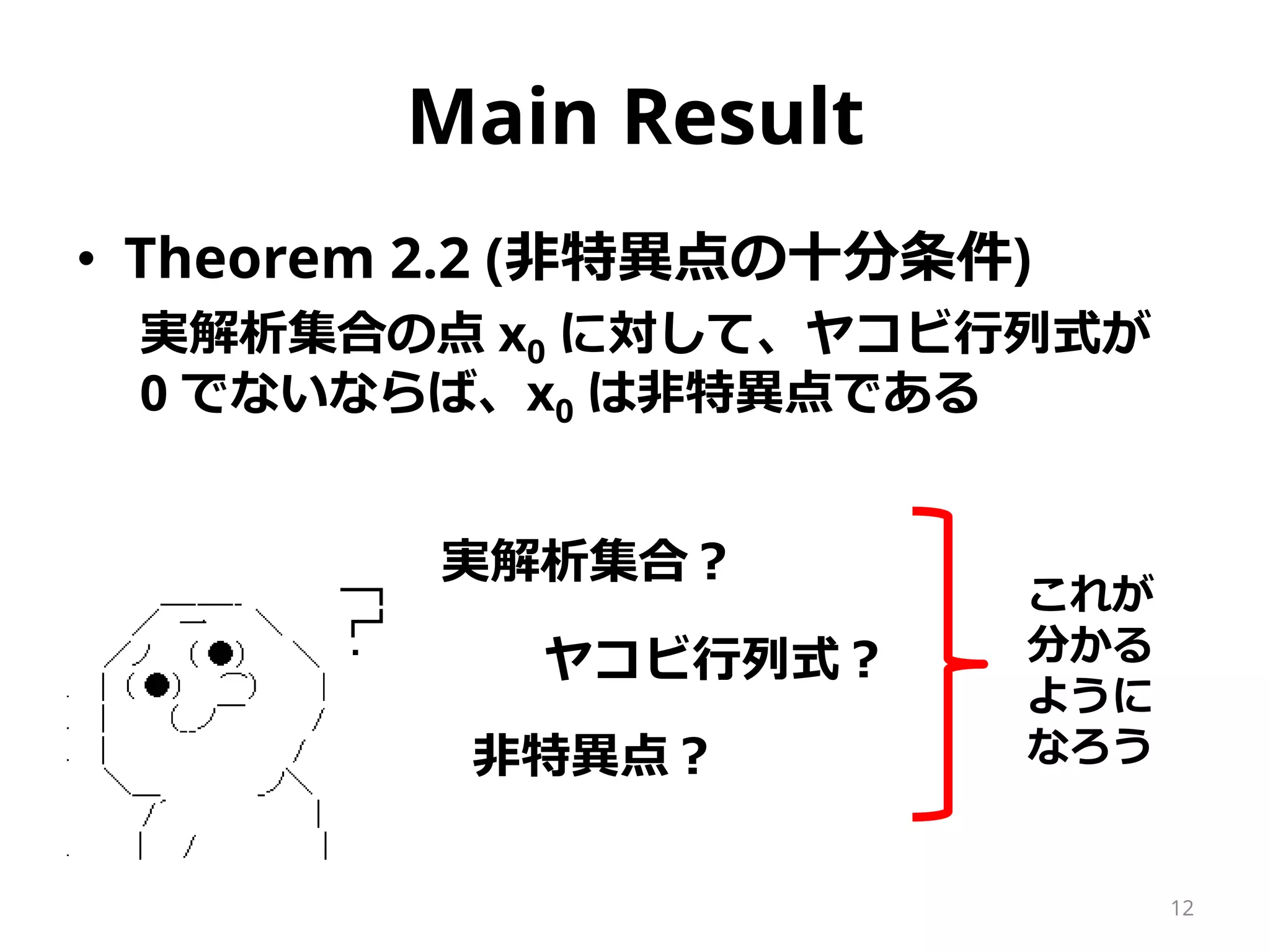
10. Main Result
• Theorem 2.2 (非特異点の十分条件)
実解析的集合の点 x0 に対して、ヤコビ行列式
が 0 でないならば、x0 は非特異点である
10
実解析的集合？
ヤコビ行列式？
非特異点？
これが
分かる
ように
なろう

11. 発表の流れ
• 2章序文
• 2.1 多項式と解析関数
• 2.2 代数的集合と解析的集合
• 2.3 特異点(前半)
• 2.3 特異点(後半)
• まとめ
11

12. 2. Singularity Theory 序文
• 統計モデルと機械学習モデルの多くは、
パラメータ空間に特異点を含んでいる
• 特異点は学習過程のふるまいを決定する
ため、特異点を理解せずに統計的学習理
論は会得できない
• 本章では、特異点の定義と特異点解消に
関する基本的な定理を導入する
• 多様体は 2.6 で導入する (担当外)
12

13. 地図
13
① 多項式 f ② 解析関数 f
③ 代数的集合
{ x; f(x) = 0}
④ 解析的集合
{ x; f(x) = 0}
⑤ 特異点

14. 発表の流れ
• 2章序文
• 2.1 多項式と解析関数
• 2.2 代数的集合と解析的集合
• 2.3 特異点(前半)
• 2.3 特異点(後半)
• まとめ
14

15. 2.1 多項式と解析関数
• このセクションでは
– 多項式の定義
– 解析関数の定義
– Cr 級関数の定義
を行う
15

16. 多項式(polynomial)
• d次元マルチインデックス
α = (α1, α2, …, αd) αi ∈ N
• x, b ∈ Rd
aα(x - b)α = aα(x1-b1)α1(x2-b2)α2 (xd-bd)αd
• べき級数(power series)
f(x) = Σα1 Σαd aα(x - b)α = Σα aα(x - b)α
• 多項式とは非ゼロ項が有限個のべき級数
…
…
16

17. 多項式の例
• f(x, y, z) = x3y5z2 + xy6 + z5 + 2
– d = 3
– a3,5,2 = 1
– a1,6,0 = 1
– a0,0,5 = 1
– a0,0,0 = 2
– otherwise aα = 0
– b = (0, 0, 0)
17

18. 解析関数(analytic function)
• 絶対収束(absolutely convergent)
開集合 U ⊂ Rd が与えられたとき、
任意の x ∈ U に対して
Σα |aα||x - b|α < ∞
• 発散しない関数 f: U → R がべき級数から
得られる
• この f(x) を実解析関数と呼ぶ
• ( f: U → C なら複素解析関数)
18

19. 解析関数
• 解析関数 f(x)
f(x) = a0 + a1(x - b) + a2(x - b)2 + …
• f(x) はテイラー級数になっている
• 無限回微分可能
• 係数
19

20. 解析関数の例
• べき級数
は |x|, |y| < ∞ で絶対収束する
• このときの解析関数
f(x, y) = exp(x + y)
20

21. 定義 2.1 Cr級関数
• d次元ユークリッド空間 Rd の開集合 U
• 関数 f: U → Rd’ が Cr 級関数であるとは
が well defined かつ連続であり
n1 + n2 + ・・・ + nd ≦ r
が成り立つときを言う(ni ∈ N)
21

22. Cr級関数
• f(x) が Cr 級関数ならば、0 ≦ r’ ≦ r に対
して f(x) は Cr’ 級関数でもある
• 全ての r ∈ N に対して f(x) が Cr 級関数で
あるとき C∞ 級関数と呼ぶ
• f(x) が実解析関数のとき Cω 級関数と呼ぶ
22

23. 発表の流れ
• 2章序文
• 2.1 多項式と解析関数
• 2.2 代数的集合と解析的集合
• 2.3 特異点(前半)
• 2.3 特異点(後半)
• まとめ
23

24. 地図
24
① 多項式 f ② 解析関数 f
③ 代数的集合
{ x; f(x) = 0}
④ 解析的集合
{ x; f(x) = 0}
⑤ 特異点

25. 2.2 代数的集合と解析的集合
• このセクションでは
– 代数的集合の定義
– 解析的集合の定義
を行う
25

26. 定義 2.2 代数的集合
• 多項式 f: Rd → R に対して
V(f) = { x ∈ Rd; f(x) = 0}
を実代数的集合と呼ぶ
• 複数の多項式 f1, f2, …, fk に対して
V(f1,…,fk) = { x∈Rd; f1(x)=…=fk(x)=0 }
これも実代数的集合と呼ぶ
26

27. 代数的集合の例
• V(y2 – x3 – ax2)
アニメーションが
動きます
27

28. 定義2.3 解析的集合
• 実解析関数 f: U → R に対して
{ x ∈ U; f(x) = 0}
を実解析的集合と呼ぶ
• 複数の実解析関数 f1, f2, …, fk に対して
{ x ∈ U; f1(x) = … = fk(x) = 0 }
これも実解析的集合と呼ぶ
28

29. 解析的集合の例
• { (x,y)∈R2; cos(x) - sin(y) = 0 }
• { (x,y,z)∈R3; exp(xy) + exp(yz) + z3 = 0 }
• { (x,y,z)∈U; x2 – ylog(z) = 0 }
– ただし U = { (x,y,z); x,y,z∈R, z > 0 }
29

30. 発表の流れ
• 2章序文
• 2.1 多項式と解析関数
• 2.2 代数的集合と解析的集合
• 2.3 特異点(前半)
• 2.3 特異点(後半)
• まとめ
30

31. 地図
31
① 多項式 f ② 解析関数 f
③ 代数的集合
{ x; f(x) = 0}
④ 解析的集合
{ x; f(x) = 0}
⑤ 特異点

32. 2.3 特異点 (前半)
• このセクションでは
– 勾配ベクトルの定義
– 関数の停留点の定義
– 極大点、極小点の定義
– 同型および解析的同型の定義
– 特異点の定義
– 特異点の例
32

33. 勾配ベクトル
• 開集合 U⊂Rd と C1 級関数 f: U→R
• f(x) の勾配ベクトルとは
33

34. 定義2.4 停留点(Critical Point)
• 開集合 U⊂Rd と C1 級関数 f: U→R
• x*∈U が f の停留点であるとは
∇f(x*) = 0
が成り立つことをいう
34

35. 極大点、極小点
• 停留点 x* を含み
f(x) ≦ f(x*) ∀x∈U’
を満たす開集合 U’⊂U が存在するとき
x* を極大点という
f(x) ≧ f(x*) ∀x∈U’
をみたす開集合 U’⊂U が存在するとき
x* を極小点という
35

36. 極大点、極小点
• f が C1 級の関数であるならば、極大点と
極小点は停留点である
• しかし、停留点が常に極大点または極小
点になるとは限らない
• 鞍点(saddle point)となる場合がある
36

37. Example 2.4
• f(x, y) = x2 + y4 + 3
– 唯一の極小点 (0,0) を持つ
• f(x, y, z) = (x + y + z)4 + 1
– x+y+z = 0 を満たす組み合わせは全て極小点
• f(x, y) = x2 – y2
– 極大点、極小点を持たない
– (0,0) は停留点であり、鞍点と呼ばれる
37

38. 定義 2.5 Cr 同型写像
• 実ユークリッド空間 Rd の開集合 U,V∈Rd
• 一対一写像 f: U → V が存在し、
• f と f-1 が Cr 級の関数であるとき、
• U と V は同型といい、f を同型写像という
• f と f-1 が解析関数であるとき、
• U と V は解析的同型といい、
• f を解析的同型写像という
38

39. 同型写像の例
• 2つの開集合
U = { (x, y) ; x2 + y2 < 1 }
V = { (x’, y’) ; x’2 + y’2 + 2y’ex’ + e2x’ < 1 }
は解析的同型である
∵ (x, y) → (x, y – ex) は解析的同型写像
39

40. 定義 2.6 特異点 (1)
• 実ユークリッド空間 Rd の空でない部分集
合 A に対して、
• P ∈ A が非特異(nonsingular)であるとは、
• P を含む開集合 U, V ⊂ Rd と
• 解析的同型写像 f: U → V が存在して
f(A∩U) = { (x1,…,xr, 0,…,0); x∈Rd }∩V
• が成り立つことをいう
40

41. 定義 2.6 特異点 (2)
• すべての P ∈ A が非特異のとき
• A を非特異集合と呼ぶ
• P ∈ A が非特異でないとき、
• P を A の特異点(singularity)と呼ぶ
• 特異点集合(singular locus)
Sing(A) = { P ∈ A; P は A の特異点 }
41

42. Example 2.6 (1)
• A = { (x, y); y – x3 = 0} は非特異集合
• P = (0, 0) に対して
• U = V = { (x, y); |x| < 1 } とすると
• (x, y) → (x, y – x3) は解析的同型写像
42

43. (x, y) → (x , y – x3)
43
(x1, …, xr, 0, …, 0)

44. Example 2.6 (2)
• A = { (x, y, z); (xy + z)2 = 0 } は非特異集合
• P = (0, 0, 0) に対して
• U = V = { (x, y, z); |x| < 1, |y| < 1 }
• (x, y, z) → (x, y, xy + z) は解析的同型写像
44

45. Example 2.6 (3)
• A = { (x, y); xy = 0 }
• P = (0, 0) は特異点
45

46. Example 2.6 (4)
• A = { (x, y); y2 – x3 = 0 }
• P = (0, 0) は特異点
• 尖点(cusp)という
46

47. Example 2.6 (5)
• A = { (x, y); x5 – y3 = 0 }
• P = (0, 0) は特異点
• 特異点に接線
47

48. Example 2.6 (6)
• A = { (x, y, z); xyz = 0 }
Sing(A) = { (x,y,z); x=y=0 or x=z=0 or y=z=0 }
• B = { (x, y, z); x = y = 0 } は非特異集合
• B ⊂ Sing(A)
• 特異点集合に含まれる非特異集合
48

49. Remark 2.1 (1)(2)
• 非特異解析的集合は実解析的多様体
– 非特異点の近傍は、実ユークリッド空間の
r次元開集合と解析的同型
– r は (x1, …, xr, 0, …, 0) の r
• 非特異点では接平面が定義可能
– 特異点では一般に接平面が定義不可能
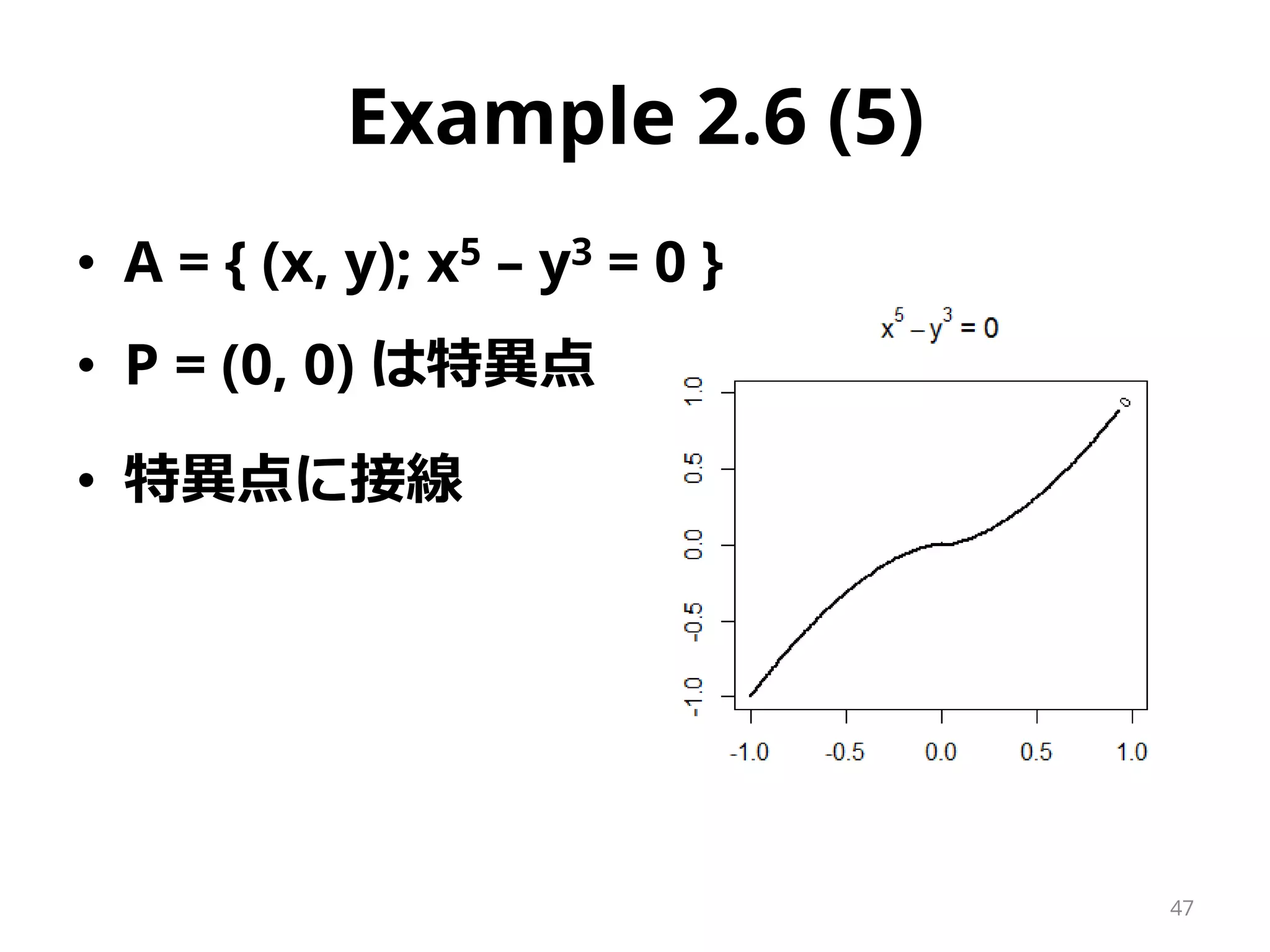
– 例外：Example 2.6 (5)
https://en.wikipedia.org/wiki/Tangent_space
49

50. Remark 2.1 (3)(4)
• 代数的集合の点 P が特異点かどうかは、
ヤコビ行列の状態によって判別できる
– 定理 2.2 で述べる
• f の停留点は実解析的集合 {x; f(x) = 0} の
特異点ではない場合がある (系2.1で述べる)
– Ex. 2.6 (1) 非特異点かつ停留点でない
– Ex. 2.6 (2) 非特異点かつ停留点 ← これ
– Ex. 2.6 (3)(4)(5) 特異点かつ停留点
50

51. 発表の流れ
• 2章序文
• 2.1 多項式と解析関数
• 2.2 代数的集合と解析的集合
• 2.3 特異点(前半)
• 2.3 特異点(後半)
• まとめ
51

52. 2.3 特異点 (後半)
• このセクションでは
– ヤコビ行列
– 定理 2.1 逆関数定理
– 定理 2.2 非特異点の十分条件
– 陰関数定理
– 特異点と停留点の関係
– Sard の定理
52

53. ヤコビ行列 (Jacobian)
• 開集合 U ⊂ Rd
• C1 級関数 f: U → Rd
– f(x) = (f1(x), f2(x), …, fd(x))
• ヤコビ行列とは
• ヤコビ行列式 det J(x)
53

54. 定理 2.1 逆関数定理
• 開集合 U ⊂ Rd と
• Cr 級関数 f: U → Rd に対して
• ヤコビ行列が x0 ∈ U で可逆(invertible)
すなわち逆行列を持つならば
• U’ と f(U’) が Cr 同型となるような開集合
U’ ⊂ U が存在する
• 逆関数定理として良く知られているため
証明は省略する
54

55. 定理 2.2 非特異点の十分条件
• 実ユークリッド空間 Rd の開集合 U
• 解析関数 f1(x), f2(x), …, fk(x) (k ≦ d)
• 実解析的集合
A = { x ∈ U; f1(x) = f2(x) = … = fk(x) = 0 }
• x0∈A が次を満たすならば x0 は非特異点
55

56. 定理 2.2 証明 (1)
• k ≦ d より、(d – k) 個の関数を追加する
fi(x) = xi (k < i ≦ d)
• f(x) = (f1(x), f2(x), …, fd(x)) は定理 2.1 の
条件を満たす(det J(x0) ≠ 0 ⇔ 可逆)
• したがって、x0 を含み
• f: V → f(V) が解析的同型写像となるよう
な開集合 V が存在する
56

57. 定理 2.2 証明 (2)
• このとき、
• x = (x1, …, xd) ∈ A∩V ならば
• f1(x) = f2(x) = … = fk(x) = 0 である
• x0 ∈ A∩V なので
• f(x0) = (0, …, 0, xk+1, …, xd) ∈ f(V)
• 定義 2.6 より x0 は特異点でない (証明終)
57

58. Main Result
• Theorem 2.2 (非特異点の十分条件)
実解析的集合の点 x0 に対して、ヤコビ行列式
が 0 でないならば、x0 は非特異点である

59. Remark 2.2 陰関数定理 (1)
• 定理 2.2 の証明より
f-1: (0, …, 0, xk+1, …, xd) → (x1, …, xd) ∈ A∩V
• この関数は x^ = (xk+1, …, xd) ∈ Rd-k から
Rd への写像とみなせる
• これを g(x^) と書く
• π(x1, …, xd) = (x1, …, xk) と定義すると
• φ(x^) = π(g(x^)) は次を満たす (次ページ)
59

60. Remark 2.2 陰関数定理 (2)
• φ(x^) = π(g(x^)) は次を満たす
f1(φ(x^), x^) = 0
・・・
fr(φ(x^), x^) = 0
• すなわち、定理 2.2 の条件を満たすとき、
このような φ が存在する
• これを陰関数定理という
60

61. Remark 2.3
• 一般化ヤコビ行列 (k×d) (k≦d)
– rank J(x0) = k ⇒ x0 は非特異 は成り立つ
– x0 が非特異 ⇒ rank J(x0) = k は成り立たない
– 第3章で x0 が非特異 ⇔ rank J(x0) = k となる
条件を見る
61

62. Corollary 2.1
• 実解析関数 f に対して、
• 実解析的集合 A = { x; f(x) = 0 } の特異点は
• 関数 f の停留点である。
• 一方、関数 f の停留点は
• A の特異点とならないこともある
62

63. Corollary 2.1 (証明)
• 定理 2.2 より
• x0 が f の停留点(勾配ベクトル=0)でないな
らば
• x0 は特異点でない
• 一方、f(x, y) = (x + y)2 は
• P = (0, 0) が停留点であるが
• (0, 0) は特異点でない
63

64. Remark 2.4
• (1) Sard の定理
– C∞ 級の関数 f : U → Rd
– Rd のすべての停留値の集合のルベーグ測度は
0 である
• (2) (定理2.9で述べる)
– 実解析関数 f の定義域が、コンパクト集合に
制限されるならば
– すべての停留点からなる集合は有限集合
64

65. 発表の流れ
• 2章序文
• 2.1 多項式と解析関数
• 2.2 代数的集合と解析的集合
• 2.3 特異点(前半)
• 2.3 特異点(後半)
• まとめ
65

66. まとめ
66出典：得能 正太郎『NEW GAME! (4)』